iBusiness
Vol.06 No.03(2014), Article ID:50231,6 pages
10.4236/ib.2014.63015
Bai-Perron Estimates of OECD Natural Rates of Unemployment 1955-2011
Michael Shannon, Bakhtiar Moazzami
Department of Economics, Lakehead University, Thunder Bay, Canada
Email: mshannon@lakeheadu.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 July 2014; revised 31 August 2014; accepted 26 September 2014
ABSTRACT
Bai and Perron’s method for detecting multiple, unknown structural breaks was used to estimate natural rates of unemployment for 19 OECD countries from 1955-2011. Natural rates were lowest in the early period, then, rose in the mid-1970s and early-1980s in most countries. Several countries saw declines in the late-1990s or early-2000s.
Keywords:
Natural Rate, NAIRU, Unemployment, Structural Break

1. Introduction
Bai and Perron [1] ’s method for detecting multiple, unknown structural breaks was used to estimate natural rates of unemployment for 19 OECD countries during 1955-2011. This updated earlier work by Papell, Murray and Ghiblawi [2] .
2. Data
The period covers from 1955-2011. The OECD’s annual harmonised unemployment rate series is the starting point. For countries where the harmonised series does not reach back to 1955, harmonised data is combined with the OECD’s earlier standardised unemployment rate series1.
3. Method
The estimation method assumes that actual unemployment rates fluctuate around a long-run equilibrium that is subject to structural shifts. For it to be appropriate, the underlying series should be stationary. The presence of a unit root is rejected in 14 countries but not for Australia, France, New Zealand, Spain and the UK2. The Bai and Perron [1] method is used to find the structural breaks. This involves finding the “best” combination of L possible breaks subjected to the constraint that distance between break intervals should be above some minimum length. Here “best” means minimum sum of squared residuals from an OLS regression of the actual unemployment rate on a set of dummies indicating the timing of the breaks. Equation (10) from Bai and Perron [1] is used to test the null of L breaks vs. the alternative of L + 1 breaks. This test is done initially for L = 0 and if the null is rejected for L = 1, 2 etc. until the test fails to reject the null. The procedure yields the optimal number of breaks and OLSestimates of the mean unemployment rate during each interval―these means serve as the natural rate estimates3.
The resulting natural rate estimates are constant in time intervals between breaks while the actual unemployment rate fluctuates around it. This is consistent with the natural rate being some longer-run equilibrium value. Phillips curve based methods relying on the HP filter (see Ball and Mankiw [3] ) give natural rate estimates that approximate smoothed versions of the actual unemployment rate series while, Kalman-filter based estimates can show so little variation over time that they give implausibly long periods when the actual unemployment is either above or below the natural rate, see Laubach [4] . The structural break approach avoids these problems but has some weaknesses. One is its inability to allow for gradual changes in the natural rate, while a second is the danger that a prolonged recession will be interpreted as a change in the natural rate.
4. Estimates
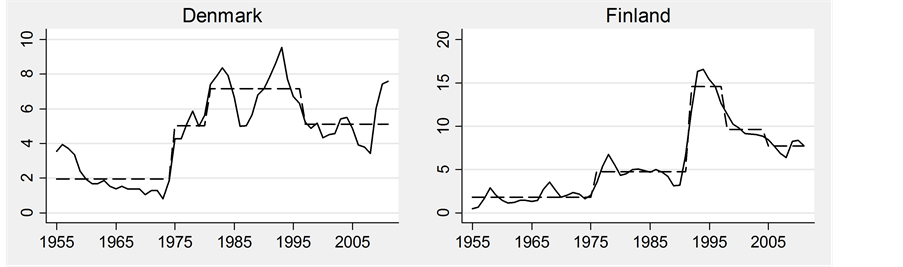
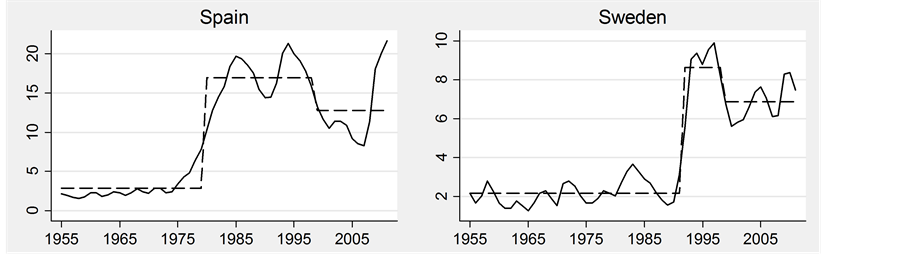
The estimates are reported in Table 1 and Figure 1. The Bai-Perron method finds equal numbers of countries with two, three or four as the optimal number of natural rate changes 1955-2011. Belgium is unusual in that it has a single break. The lowest natural rate estimates are found either at the very start of the sample (14 countries) or starting in 1961 (4 countries). Ireland’s during 1998-2005 is the exception. Most countries had minimum natural rates between 1.3% and 2.8%. Peak estimates are at the end of the sample for Austria, Belgium, France, Germany, Switzerland and Japan. Peaks for the UK, US and Netherlands occurred in the 1980s while the remaining 10 countries only fell from their peaks in the mid-to-late 1990s. The highest estimates were for Ireland, Finland and Spain (>14%), followed by the UK and Italy (10.4% and 10.9%). Most countries had a maximum of between 7.2% and 9.4% while 5 had maxima below 6%. The difference between the maximum and minimum estimates was 4 percentage points or less in Austria, Switzerland, Norway, Japan, US and Canada. At the other extreme, Finland and Spain had ranges of 12.7% and 14.1% respectively.
The Spanish estimates suggest that the 14.1% range is the result of a single jump in 1979-1980. Other countries with large single year jumps were Finland (9.8% in 1991-1992), and Ireland (8.3% in 1981-1982). Several countries had single jumps of just over or just under 4%.
All but three countries (Belgium, France and Switzerland) experienced a decline in their natural rates estimates sometime during 1955-2011. Typical declines were small compared to the largest single-year increases. In 9 countries the declines were −0.8% to −2.2%, 4 saw falls of between −3.1% and −4.9%. Ireland is an outlier with a fall of −9.4% in 1997-1998.
Jumps in the natural rate estimates across countries were concentrated in particular time periods. Germany, Japan, Italy and Austria all saw declines in 1961. Remarkably, there were no breaks in any of the countries between 1962 and the mid-1970s. 11 countries saw increases in the mid-1970s and 14 in the first half of the 1980s. US, Netherlands and the UK saw falls 1987-1988. Two countries saw increases in 1989 and another three in 1992. 13 declines occurred during 1997-2001. The effects of common shocks affecting many labour markets simultaneously, similar responses to the same macroeconomic shocks or common trends in labour market policy and institutions are possible reasons for this clustering.
5. Discussion and Conclusions
The estimated patterns are plausible in that there are few large, persistent gaps between actual and natural rates.
Table 1. Structural breaks and natural rate estimates (%), 1955-2011.
Note: Assumes aminimum span of 6 years. Optimal no. of breaks determined using Bai and Perron’s (1998) FT(L + 1/L) test of L vs. L + 1 breaks (see their Equation (10)).

Figure 1. Actual and natural unemployment rates 1955-2011.
There were, however, a few episodes where natural rates are high for implausibly short periods (the Nordic countries, New Zealand and Italy in the 1990s, the UK and Netherlands in the 1980s). In these cases the method is likely treating a somewhat persistent recession as a rise in the natural rate. For some countries, multiple jumps in natural rates occur within a short-time span suggesting that the Bai-Perron method may be interpreting a trend as a series of jumps.
Papell, Murray and Ghiblawi [2] used a version of Bai-Perron’s method for 16 OECD countries during 1955-1997. Their results and those here are quite similar. No country is found to have a constant natural rate. Even with the extra 14 years of data here, the number of breaks found remains small, consistent with natural rates that experience occasional changes rather than hysteresis. The timing of breaks on the common 1955-1997 sample is similar. Papell et al. do find more breaks during the overlap period in eight countries and in some cases timing of breaks is slightly different. Disagreements reflect differences in the underlying data and partly differences in the test used to determine the number of breaks (Papell et al. uses the sequential version of the Bai-Perrontest).
The OECD generates regular natural rate estimates using a Phillips curve based method from Laubach [4] , see Guichard and Rusticelli [5] . Their results are broadly similar to those presented here (low rates early in the sample periods, increases in the mid-late 1970s and early 1980s and often some decline in the late 1990s). The main difference is that the Bai-Perron method gives natural rate estimates that change in discrete jumps while methods like the OECD estimates change gradually.
A large literature has arisen concerned with evolution of differences in national unemployment rates, Blanchard [6] provides an overview. The consensus suggests that macroeconomic shocks in the mid-1970s lead to increases in unemployment which were more severe and persistent in countries where rigidities kept wages high. Some combination of rigidities and policy responses to high unemployment pushed up the natural rate in the mid-1970s. The more heterogeneous experiences across countries since the 1980s reflected differences in, and changes to, institutions and interactions of institutions with shocks, see Ljungqvist and Sargent [7] . Changes in policies and institutions in the 1990s (less generous income support, less employment protection worked to bring natural rates down in several countries (Boeri and Garibaldi [8] ). This pattern of shocks, their interaction and effects on policies and institutions seems broadly consistent with the patterns in natural rate estimates found here. The experience of the 1970s and 1980s suggest possible future rises in natural rates if policy and institutional responses to current downturns are like those in the earlier period.
References
- Bai, J. and Perron, P. (1998) Estimating and Testing Linear Models with Multiple Structural Breaks. Econometrica, 66, 47-78. http://dx.doi.org/10.2307/2998540
- Papell, D., Murray, C. and Ghiblawi, H. (2000) The Structure of Unemployment. Review of Economics and Statistics 82, 309-315. http://dx.doi.org/10.1162/003465300558696
- Laurance, B. and Mankiw, N.G. (2002) The NAIRU in Theory and Practice. Journal of Economic Perspectives, 16, 115-136. http://dx.doi.org/10.1257/089533002320951000
- Laubach, T. (2001) Measuring the Nairu: Evidence from Seven Economies. The Review of Economics and Statistics, 83, 218-231. http://dx.doi.org/10.1162/00346530151143761
- Guichard, S. and Rusticelli, E. (2011) Reassessing the NAIRUs after the Crisis. OECD Economics Department Working Papers No. 918.
- Blanchard, O. (2006) European Unemployment: The Evolution of Facts and Ideas. Economic Policy, 21, 5-59. http://dx.doi.org/10.1111/j.1468-0327.2006.00153.x
- Ljungqvist, L. and Sargent, T. (2008) Two Questions about European Unemployment. Econometrica, 76, 1-29. http://dx.doi.org/10.1111/j.0012-9682.2008.00816.x
- Boeri, T. and Garibaldi, P. (2009) Beyond Eurosclerosis. Economic Policy, 406-461.
- Layard, R., Nickell, S. and Jackman, R. (1994) The Unemployment Crisis. Oxford University Press, Oxford.
- Bundesagentur für Arbeit 2011 (2002) Amtliche Nachrichten der Bundesagentur für Arbeit. http://statistik.arbeitsagentur.de/
- Burda, M. and Hunt, J. (2011) What Explains the German Labor Market Miracle in the Great Recession? Brookings Paper on Economic Activity, 273-319. http://dx.doi.org/10.1353/eca.2011.0004
- Elliott, G., Rothenberg, T. and Stock, J. (1996) Efficient Tests for an Autoregressive Unit Root. Econometrica, 64, 813-836. http://dx.doi.org/10.2307/2171846
- Perron, P. and Vogelsang, T. (1992) Nonstationarity and Level Shifts with an Application to Purchasing Power Parity. Journal of Business and Economic Statistics, 10, 301-320.
- Clemente, J., Montanes, A. and Reyes, M. (1998) Testing for a Unit Root in Variables with a Double Change in the Mean. Economic Letters, 59, 175-182. http://dx.doi.org/10.1016/S0165-1765(98)00052-4
- Kerekes, M. (2011) Analyzing Patterns of Economic Growth: A Production Frontier Approach. Unpublished Manuscript.
NOTES

1When joining the series, it is assumed that the year-to-year proportional changes in the harmonised and standardized rate are the same. The standardised rate data is from Layard, Jackman and Nickell ( [9] , Table A3) and from OECD Economic Outlook. The German data is for West Germany. The 1991-2011 West German unemployment rates are from Bundesagentur für Arbeit [10] , earlier German data is from Burda and Hunt [11] and Layard et al. [9] .

2A standard ADF test, Elliot et al.’s [12] GLS variant of the ADF test and tests that allow for changes in the series mean from Perron and Vogelsang [13] and Clemente et al. [14] were used.
3A STATA program from M. Kerekes [15] was used to find the breaks. The estimates reported set minimum interval length at 6 years; alternatives assuming minimum spans of 5 or 7 years gave similar results.