Journal of Geographic Information System
Vol.07 No.04(2015), Article ID:58652,14 pages
10.4236/jgis.2015.74029
Spatial Modeling of Residential Crowding in Alexandria Governorate, Egypt: A Geographically Weighted Regression (GWR) Technique
Shawky Mansour
Department of Geography and GIS, Faculty of Arts, Alexandria University, Alexandria, Egypt
Email: gisshawky@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2015; accepted 4 August 2015; published 7 August 2015
ABSTRACT
Despite growing research for residential crowding effects on housing market and public health perspectives, relatively little attention has been paid to explore and model spatial patterns of residential crowding over space. This paper focuses upon analyzing the spatial relationships between residential crowding and socio-demographic variables in Alexandria neighborhoods, Egypt. Global and local geo-statistical techniques were employed within GIS-based platform to identify spatial variations of residential crowding determinates. The global ordinary least squares (OLS) model assumes homogeneity of relationships between response variable and explanatory variables across the study area. Consequently, it fails to account for heterogeneity of spatial relationships. Local model known as a geographically weighted regression (GWR) was also employed using the same response variable and explanatory variables to capture spatial non-stationary of residential crowding. A comparison of the outputs of both models indicated that OLS explained 74 percent of residential crowding variations while GWR model explained 79 percent. The GWR improved strength of the model and provided a better goodness of fit than OLS. In addition, the findings of this analysis revealed that residential crowding was significantly associated with different structural measures particularly social characteristics of household such as higher education and illiteracy. Similarly, population size of neighborhood and number of dwelling rooms were found to have direct impacts on residential crowding rate. The spatial relationship of these measures distinctly varies over the study area.
Keywords:
Spatial Modelling, OLS, GWR, Residential Crowding, Alexandria Neighborhoods

1. Introduction
Within the field of spatial analysis and urban growth, environmental quality of housing has given much attention to geographic research. However, little attention has been paid to investigate and model spatial structure of residential crowding phenomena. In most cases, residential crowding is clearly seen as a marker of housing inequality and it is considered an evidence of urban deprivation. The purpose of this study is to measure and examine the spatial patterns of overcrowding across Alexandria neighborhoods and model the relationships between crowding rates and associated set of socio-demographic variables. Such this measure provides a robust assessment of overcrowding in a developing world city. Moreover, both Ordinary Least Squares (OLS) and Geographically Weighted Regression (GWR), as advanced modelling techniques, were employed to explore non-stationary relationships between residential overcrowding and socio-demographic measures in Alexandria neighborhoods. These techniques are valuable in analyzing spatial characteristics of residential crowding particularly geographic patterns, distribution variations, and determining factors that are strongly correlated with the problem, for instance, population size, dwelling room number, and other social explanatories such as education and illiteracy of population living in Alexandria neighborhoods.
Urban growth in most cities of developing world has created unplanned housing cores that suffer shortage in access to basic need supplies such as drinking water and electricity. However, the increase of population size with the lack of housing availability and affordability are the most likely causes of urban sprawl. Urban land supply for residential development has direct impacts on housing policies and consumption [1] . The change in land use forms and urban sprawl lead to residential overcrowding and poor quality of life. Much of the large literature on urban sprawl especially in the developing world pays a particular attention to spatial and socioeconomic factors impacting urban expanding (e.g. Sudhira et al. [2] ; Lata et al. [3] ; Yeh and Xia [4] ). For instance in China, housing consumption and residential crowding have received considerable attentions especially in urban areas (Chen et al. [5] ; Yu [6] ; Li and Huang [7] ). Various variables in Chinese urban communities were identified to influence residential crowding for instance city size, household income, housing tenure and life cycle. However, household income factor is substantially considered the most important determinant of residential crowding [8] . In most European countries such as Germany, foreigners and non-native population are more likely to live in overcrowding housing than native population [9] . A person per room is usually used as a basic indicator for measuring overcrowding. The bathrooms, hallways and closets are not included in the room count [10] . Residential overcrowding is defined as more than one person per room in a housing unit. In addition, there are other popular measures of housing crowding including the total number of people in a unit and the ratio of persons to floor space in square feet. According to the 1985UK housing Act [11] , overcrowding was defined based upon room standards as “a dwelling is overcrowded when two persons from opposite genders who are not living together as a husband and wife must sleep together in the same bedroom”.
Modelling housing demand was applied as a function of environmental, structural and characteristics of neighborhood. The United Nation Habitat Program for Hosing has estimated that African households need around 4 million housing unit per year and over 60% of housing demand in urban areas is still required to accommodate residents [12] . From public health perspective, many studies have considered the relationships between higher rates of morbidity and mortality and residential overcrowding in the developed and developing countries (Acevedo-Garcia [13] ; King [14] ; Williams and Collins [15] ; Reitmanova and Gustafson [16] ). It has been argued that overcrowding has a negative impact on population health and it is considered as a risk for infectious disease. For instance, a strong association was found between crowded dwellings and acute rheumatic fever [17] . It has conclusively been shown that household crowding increases risk of psychological illness [18] . Likewise, violent crime, physical disorder and residential crowding were found geographically to be higher correlated than other factors with social stressors. Overcrowding and low access to open spaces might be significantly associated with asthma disease [19] . Population density was presented as a main explanatory variable of death rate in the most deprived areas [20] . Health problems among adolescents were found to be correlated with residential densities in Nigeria [21] . Dhonte et al. [22] pointed out that new demographic conditions in most of the Middle East countries specifically population growth had exerted significant influence on residential overcrowding. As a result, overcrowding has been seen as a significant issue on public health and quality of life of population. Population growth and average of family size variables were formed as major estimators to predict housing needs in cities of Jordon [23] .
Baker et al. [24] reported that 10.45 of the total population was exposed to household crowding (1+ bedroom deficit). Significant impacts of ethnicity and tenure on household crowding were highlighted where crowding rate was higher among pacific people and rental houses. Olmos and Garrido [25] carried out a study of residential crowding among African immigrants in Spain. The findings revealed a correlation between household overcrowding and various socioeconomic factors particularly isolation and segregation, low income, lower housing price and inadequate accessibility to public facilities. Even in the developed countries, increased household overcrowding might be a natural response to high housing price, unaffordability of housing, low income and higher rent prices. In the USA, increasing in overcrowding rate was reported in most of counties. Another noteworthy fact is that residential crowding rate is greater among nonwhite, ethnic minorities and districts where immigrant population is living [26] .
In the most populous Arab countries such as Egypt, poor housing conditions and poverty are increasingly spreading across informal settlements and slums. The issue of slums in Egypt is much related to unplanned and unsafe areas where there are a quite shortage in the basic human needs and service coverage such as electricity, safe drinking water and sanitation. Slums are characterized by deprivation, rural-urban migration, unemployed persons, and high rate of crime, inequalities and insecurity. In the big Egyptian cities such as Alexandria, informal and unplanned settlements have been predominantly found in most of its neighborhoods. The most likely causes of this kind of settlements are rapid population growth and urban expansion, migration from rural regions in the nearest Delta governorates to the city. Highlighting the association between overcrowding rate and mortality in Alexandria, Khalifa [27] discussed the challenges of detecting and determining the actual area size of slums (Ashwa’aiat) across Egyptian governorate. The main reason is lack of spatial data where there is no any map representing slum areas in each administrative boundary. Consequently, predicting population size living in these areas is quite difficult. Likewise, the absence of integrated definition of slums and the distinction between unplanned, informal settlements and slums make it quite difficult to find out the slum area size accurately. Mohamed et al. [28] pointed out that high spatial correlation between crowding index and high rate of child mortality less than 5 years old was identified in neighborhoods of Alexandria such as Al Amria and Borg Al-Arab. They found that socioeconomic and environmental variables had direct impacts on the higher mortality rate particularly low percentage of potable drinking water supply and electricity and low percentage of household accessibility to adequate sewage.
2. Study Area and Data
2.1. Study Area
Alexandria governorate lies along the Mediterranean coast and stretch for about 70 km northwest of the Nile Delta. The governorate is bounded by the Mediterranean Sea in the north, El Behera governorate in the south and the east and Matrouh governorate in the west (Figure 1). The total area size of Alexandria governorate is almost 2818 km2. It has the most important harbor in Egypt and it is the second largest urban governorate in the country with population more than four and half million (4,799,740 in March 2015) and population density of 1600/km2 according to the Central Agency for Public Mobilization and Statistics (CAPMAS). Alexandria has a unique geographical location and a mild climate. It is also considered an industrial governorate where 40% of Egyptian industries are concentrated, especially chemicals, food, spinning and weaving as well as petrol industries and fertilizers. To absorb the expected increasing number of population and settlement growth, Borg al-Arab city within the western part of the governorate was established to be an industrial and housing city.
2.2. Data
Attribute database was designed based on secondary data source from 2006 Egyptian census. Different socio- demographic variables were created in the form of quantitative type to enable constructing OLS and GWR Regression models within GIS platform. Socio-demographic factors are strongly correlated with residential crowding and they are likely to be the most effective predictors of the problem. Varity of socio-demographic variables were created as independent variables to investigate and predict residential crowding across Alexandria neighborhoods (Table 1). The spatial data are vector based layer that has 140 polygons represent Alexandria neighborhoods (Shayakhat in Arabic). This spatial layer was provided by CAPMAS. The agency is the official statistical office of Egypt that conducts census and surveys across the country and collects, processes, analyzes all statistical data. The spatial layer was projected to WGS 1984 UTM Zone 35 N and the attribute quantitative data were aggregated at neighborhood level and joined to this layer. Analysis procedures and techniques were
Figure 1. Location of Alexandria governorate in north of Egypt.
Table 1. The dependent and explanatory variables used in the regression analysis.
applied using ArcGIS software V 10.2 The dependent variable was calculated statistically in the form of ratio type to represent the number of usual residents in a household divided by the number of rooms in that household’s accommodation.
Figure 2 depicts the spatial distribution of residential crowding rate across Alexandria neighborhoods. The rate increases (red and dark red colors in the map) from the western south, the middle and in some neighborhoods located in the east of the governorate. The middle values of crowding rates appear to increase very gradually in the neighborhoods located in the middle, close to the city center, and the east of the governorate. The spatial pattern associated with lower residential crowding rates is found mainly as a long strip starting from northern neighborhoods of east and middle of the governorate. Likewise, some neighborhoods in western south show that there has been a decrease in the residential crowding rates.
3. Methodology
3.1. Techniques for Modeling Spatial Relationships
The methodology is based on standard GIS tools that enable modeling relationships between residential crowding rate and a set of socio-demographic variables.
3.1.1. Ordinary Least Squares (OLS)
Ordinary Least Squares (OLS) regression is a global linear technique used to model and examine relationships between variables based on a single equation to estimate the relationship between a dependent variable and explanatory variable (s). The model assumes a stationary relationship across the study area. This means that a single coefficient is computed and implying as a constant over space [29] . The relationship between a dependent variable (residential crowding rate) as a response discrete variable (Y) and explanatory discrete variables (X1, X2, X3...) is presented as a line of best fit. In this equation, Y variable is predicted by Xn variables. The mathematical line equation as follows:
Figure 2. Spatial distribution of crowding rate across Alexandria neighborhoods.
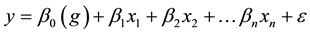 (1)
(1)
where:
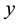 = the response variable.
= the response variable.
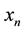 = the set of one or more independent variables.
= the set of one or more independent variables.
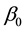 = the intercept.
= the intercept.
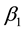 = the parameter estimate for variable 1.
= the parameter estimate for variable 1.
In this equation  is the intercept and indicating y value when it is equal to zero.
is the intercept and indicating y value when it is equal to zero. 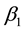 is indicating the slope of the line and represent the regression coefficient that describes the changes in the dependent variable y when x changes in one unit. Candidate independent variables were created in the same quantitative form of ratio type similar to the dependent variable.
is indicating the slope of the line and represent the regression coefficient that describes the changes in the dependent variable y when x changes in one unit. Candidate independent variables were created in the same quantitative form of ratio type similar to the dependent variable.
Scientific hypothesis of this modelling is based on the assumption that there is a significant relationship between the dependent and independent variables. Additionally, the socio-demographic variables certainly affect residential crowding problem. The degree of multicollinearity of OLS multiple regression can be checked using variance inflation factor (VIF). Any independent variable whose value is greater than 7.5 means that the variable could be considered as a linear combination of other independent variables and should be removed [30] [31] . The OLS model misspecification and the spatial independency of residuals was verified by applying spatial autocorrelation Moran’s I test for residuals clustering. This is defined by the equation:
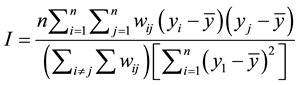 (2)
(2)
where n is the number of spatial units (neighborhood polygons) while I and j indicate various neighborhoods, yi and yj are the residuals of the two locations i and j respectively,  is the mean of y; and Wij is an element of a matrix of spatial weights.
is the mean of y; and Wij is an element of a matrix of spatial weights.
3.1.2. Geographically Weighted Regression (GWR)
GWR is a local regression technique that assumes non-stationary (non-static) in relationships between response variable and explanatory variable(s). Since the spatial relationship changes from location to another, GWR generates a single equation for each spatial unit and consequently allows regression coefficients to vary across the study area. The model calibrates each spatial unit (polygon) using the target one and its neighbors. The calibration follows Tobler’s (1970) first law of geography where higher weights are assigned to the nearby locations (polygons) according to their spatial proximity to the target location i (polygon i). The weights indicate the fact that close locations have more influence on the calibration than locations further away. The GWR model is defined as follows [32] [33] :
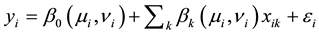 (3)
(3)
where β(ui, vi) depicts the vector of the location-specific parameter estimates, (ui, vi), donates the coordinates of geographic location i in space, βk (ui, vi) indicate a realization of the continuous surface at point i which is a continuous surface of parameter values. Applying GWR within GIS platform, local coefficient and its diagnostics (local R2, standard errors and standard deviation) are produced as parameter estimates for each spatial feature. In addition, maps of coefficient raster surfaces are generated. These represent locations where each explanatory variable shows higher or lower influence in the dependent variable [34] . To apply and perform the GWR model, the geographically weighted regression extension in the spatial statistics toolbox of ArcGIS 10.2 was used. The same response variable and explanatory variables of the OLS model were used as data input of the model.
4. Results and Discussion
4.1. The Findings of Global OLS Model
Exploratory Regression tool in ArcGIS was applied to select the best model with the optimal output parameters. Among the passing models, the best one with five explanatory variables and higher adjusted R2 was chosen. Figure 3 represents the distribution of each selected explanatory variable across the study area. Table 2 illu-
Figure 3. The selected five explanatory variables.
Table 2. Summary of results from the OLS regression analysis.
*Statistically significant at the 0.05 level.
strates the regression parameters estimates for the OLS model. The coefficients are statistically significant (P < 0.05). The values of VIF for all variables indicate that overlapping and multicollinearity are not found and there is no identified redundant variable among all explanatory variable. The sign of the regression coefficients of population size, illiteracy and one room dwelling in the model are positive, suggesting that there are positive relationships between residential crowding rate and those explanatory variables. The proportion rise of population size, illiteracy, and households living in one room dwelling in each neighborhood is associated with the rise of residential crowding rate. On the other hand, the sign of regression coefficient of higher education and five rooms dwelling variables in the model are negative, suggesting that there are a negative relationships between the response variable and those two explanatory variables. This means that each neighborhood with higher proportion of university education and higher proportion of households living in five rooms dwelling exhibits lower rate of residential crowding.
Evaluation the model performance is much related to assessing how well the linear equation fits the data. Exploring statistical values of R2 and adjusted R² is an important step in gauging the model performance. Table 3 shows the OLS model diagnosis. The explanatory variables have adjusted R2 = 0.74 which means that 74 of changes in residential crowding rates in Alexandria neighborhoods can be explained by the independent variables.
A scatter plot representing observed values versus estimated values of the dependent variable (Figure 4) also illustrates the model fit and performance. According to this evaluation, the overall performance of the model is satisfactory and thus the explanatory variables are strong predictors of residential crowding rate across Alexandria neighborhoods.
Figure 4. Scatter diagram of observed vs. predicted residential crowding rates for OLS model.
Table 3. The diagnosis of the OLS regression analysis.
Investigating the distribution pattern of the residuals, the generated standardized residual of the OLS model was mapped (Figure 5). If the residuals show spatial clustering, this means that one or more key independent variables are missing from the built model. The red color on the map describes the under predicted residual (positive values) while the blue color shows the over predicted residuals (negative values). The residual distribution indicates a random noise meaning that the over and under prediction of the model are not clustering.
Table 4 presents summary of Moran’s I autocorrelation test. The critical Z-score values (when using a 95% confidence level) are larger than −1.96 and +1.96 standard deviations (Z score = −1.11). This means that the null hypothesis (the residual values are clustered) has to be rejected and the residuals are randomly distributed. Clearly, this confirms the fact that there is no any key explanatory variable missing.
Figure 5. Spatial distribution of OLS standardized residuals.
Table 4. Diagnosis of Global Moran’s I spatial autocorrelation.
4.2. The Findings of Local GWR Model
A comparison of the two models outputs reveals that the GWR model has significant improvements over the OLS model. As a rule, model with larger R² value has a greater explanatory power. By contrast, lower Akaike’ Information Criterion (AICc) indicates a better model. The adjusted R² of the local model has increased about five percent (0.79) compared with the global model (0.74), meaning that the GWR has a significant improvement in explaining the variance of the response variable (Table 5). The AICc of the GWR model indicates that the model was better fit than the OLS since the value is lower. Furthermore, significant non-stationary relationships between residential crowding and the five explanatory variables do exist.
Figure 6 demonstrates the observed values versus the predicted values of the dependent variable for the GWR model. In comparison with Figure 4, the concentration of the scatter points and linear R² reflects better model performance. In addition to this comparison, standardized residuals values should produce a random pattern of relationship in a properly constructed regression model. Mapping the residuals of the GWR shows that they are randomly distributed (Figure 7).
Looking at the distribution of the spatial smoothing local R2 (Figure 8), it is generally obvious that the explanatory power of the GWR model was higher in the west and east neighborhoods of the governorate (local R² values 0.69 to 0.79). The model illustrates a strong significant prediction of residential crowding across those neighborhoods. The opposite trend was observed in neighborhoods located in the middle of the governorate where local R2 values are lower (between 0.69 and 0.79). Hence, the resultant spatial variation of the local R² patterns shows that the strength of the model prediction increases in the west and the east of the governorate and
Figure 6. Scatter diagram of observed vs. predicted residential crowding rates for GWR model.
Table 5. Comparison of OLS and GWR models fitness.
Figure 7. Spatial distribution of GWR standardized residuals.
Figure 8. Spatial distribution of local R2 of GWR model.
decreases in the middle parts. Furthermore, the local R² are among middle values (local R2 values 0.77 to 0.78) in the neighborhoods located close to the city center and nearby Alexandria harbor (yellow color).
Figure 9 illustrates the spatial pattern of GWR local coefficient estimate for each explanatory variable. Population size explanatory variable is an important predictor for estimating residential crowding. The influence of this variable is strong in the neighborhoods located in the middle of the governorate. While it is a margin in the east and it shows a weak influence in the west and south-west. Illiteracy was found to be positively associated with residential crowding. Neighborhoods with higher percentage of illiterate individuals tend to show higher residential crowding rate. Illiteracy as an explanatory variable has a higher influence in estimating residential crowding in the east and middle parts of the governorate. By contrast, it is a weak predicator in the south and south-west.
The local coefficient estimate of higher education variable accounts for a significant influence only in the neighborhoods located in the west of the governorate, while it is a weak predictor in the rest of the governorate. Higher education variable was found to be negatively correlated with residential crowding. There is a strong as-
Figure 9. Local parameter estimates of GWR model.
sociation between households with higher education and probability of living in non-crowded housing conditions. One room dwelling variable exhibits a strong positive influence in residential crowding over the neigh- borhoods located in the west and southwestern of Alexandria governorate. In contrast, the influence of this variable tends to be weak across the rest of the governorate. Five-room dwelling variable has a high negative influence in estimating the residential crowding over the west and southwestern. Whereas percentage of households living in five rooms dwelling is higher in those regions, steep decline in overcrowding rates can be easily identified (Figure 2). As clearly revealed by the local parameter estimates of those variables (one and five room dwelling), neighborhoods located close to Alexandria harbor show higher percentage of households living in one room.
The opposite trend was observed in the neighborhoods of east of the city center and southern west of the governorate (Figure 2). Explanation of that spatial pattern distribution perhaps is the price of dwelling and neighborhood area size. For instance, neighborhoods that are located in the east of the city center show smaller percentage of households living in one room. Households living in such areas are more likely with higher annual income, belong to upper and middle upper social classes who prefer to live in higher housing quality. The area size could be another investigation for higher percentage of households living in five rooms in neighborhoods of southern west. Interestingly, most of households live in this part of the governorate neither belong to upper nor middle upper social classes. However, they live in dwellings with higher number of rooms and this might be a result of the availability of land urban areas for settlement expansion. In addition, most of these neighborhoods exhibit low population size and dispersion of settlements. Consequently, housing prices are fairly lower compared with other Alexandria neighborhoods.
5. Conclusions
This paper set out to determine spatial effects of various socio-demographic determinates on residential overcrowding rates over Alexandria neighborhoods. GIS based global (OLS) and local (GWR) modeling was used to investigate relationships between residential overcrowding and socio-demographic variables. The analytical result reveals that it is necessary to investigate local variations of spatial relationships when residential crowding datasets essentially are non-stationary. While OLS global model often assumes homogeneity of relationships between response variable and explanatory variables, this analysis has distinctly proven that spatial relationships in residential crowding data are not static across Alexandria neighborhoods. The GWR model is more appropriate and has crucial advantages in examining and measuring spatial variations and patterns.
The socio-demographic variables in particular education, illiteracy and population size were the most important predictors and they could clearly explain variations in residential crowding. Other two significant variables that determined residential crowding rates were one-room dwelling and five-room dwelling that were found to be strongly influencing estimating residential crowding conditions. Moreover, the findings highlight the fact that population size of neighborhood specifically is more related to residential crowding than other household living condition factors (e.g. access to electricity, drinking water and sanitation).
Higher local parameter estimations were substantially found on the neighborhoods located in marginal places of Alexandria governorate whereas higher proportion of households lived in urban slums. Residential overcrowding rates are higher since a very large number of immigrants from various rural areas (e.g. Upper Egypt and Delta governorates) are more likely to live in such these neighborhoods. Married immigrants tend to have more children than other groups while single immigrants usually come to stay with their relatives who are previous immigrants established to Alexandria. Overall, this study strengthens the idea that changes in spatial patterns of residential overcrowding across Alexandria neighborhoods are not only associated with demographic conditions but also more related to household social characteristics. These facts are very important when policy makers want to evaluate the current housing status in Alexandria or designing programs for constructing subsidize housing for low-income households in order to improve their living circumstances. A key policy priority should be therefore a plan for decreasing residential crowding rates by considering the impacts of spatial and socio-demographic factors. The study is limited by the lack of aggregated data on neighborhood economic variables such as household income and housing affordability. Consequently, the available attribute data neither allow us to look at changes in residential overcrowding rates over time nor to investigate spatial patterns according to economic circumstances. Hence, farther research could identify more explanatory variables than those used in this study for better assessment and understanding of residential overcrowding.
Cite this paper
ShawkyMansour, (2015) Spatial Modeling of Residential Crowding in Alexandria Governorate, Egypt: A Geographically Weighted Regression (GWR) Technique. Journal of Geographic Information System,07,369-383. doi: 10.4236/jgis.2015.74029
References
- 1. Brueckner, J.K. (2000) Urban Sprawl: Diagnosis and Remedies. International Regional Science Review, 23, 160-171. http://dx.doi.org/10.1177/016001700761012710
- 2. Sudhira, H., Ramachandra, T. and Jagadish, K. (2004) Urban Sprawl: Metrics, Dynamics and Modelling Using GIS. International Journal of Applied Earth Observation and Geoinformation, 5, 29-39.
http://dx.doi.org/10.1016/j.jag.2003.08.002 - 3. Lata, K.M., Sankar Rao, C., Krishna Prasad, V., Badrinath, K. and Raghavaswamy, V. (2001) Measuring Urban Sprawl: A Case Study of Hyderabad. GIS Development, 5, 26-29.
- 4. Yeh, A.G.-O. and Xia, L. (2001) Measurement and Monitoring of Urban Sprawl in a Rapidly Growing Region Using Entropy. Photogrammetric Engineering and Remote Sensing, 67, 83-90.
- 5. Chen, J., Guo, F. and Wu, Y. (2011) One Decade of Urban Housing Reform in China: Urban Housing Price Dynamics and the Role of Migration and Urbanization, 1995-2005. Habitat International, 35, 1-8. http://dx.doi.org/10.1016/j.habitatint.2010.02.003
- 6. Yu, Z. (2006) Heterogeneity and Dynamics in China’s Emerging Urban Housing Market: Two Sides of a Success Story from the Late 1990s. Habitat International, 30, 277-304.
http://dx.doi.org/10.1016/j.habitatint.2004.02.010 - 7. Li, S.-M. and Huang, Y. (2006) Urban Housing in China: Market Transition, Housing Mobility and Neighborhoods Change. Housing Studies, 21, 613-623. http://dx.doi.org/10.1080/02673030600807043
- 8. Clark, W.A., Deurloo, M.C. and Dieleman, F.M. (2000) Housing Consumption and Residential Crowding in US Housing Markets. Journal of Urban Affairs, 22, 49-63. http://dx.doi.org/10.1111/0735-2166.00039
- 9. Clark, W. and Drever, A.I. (2000) Residential Mobility in a Constrained Housing Market: Implications for Ethnic Populations in Germany. Environment and Planning A, 32, 833-846.
http://dx.doi.org/10.1068/a3222 - 10. Myers, D. and Lee, S.W. (1996) Immigration Cohorts and Residential Overcrowding in Southern California. Demography, 33, 51-65. http://dx.doi.org/10.2307/2061713
- 11. The Official Home of UK Legislation (2015) 1985UK Housing Act, Definition of Overcrowding. http://www.legislation.gov.uk/
- 12. UN Habitat (2015) Housing & Slum Upgrading.
http://unhabitat.org/urban-themes/housing-slum-upgrading/ - 13. Acevedo-Garcia, D. (2000) Residential Segregation and the Epidemiology of Infectious Diseases. Social Science & Medicine, 51, 1143-1161. http://dx.doi.org/10.1016/S0277-9536(00)00016-2
- 14. King, N.B. (2003) Immigration, Race, and Geographies of Difference in the Tuberculosis Pandemic. In: Gandy M. and Zumla, A. Eds., Return of the White Plague: Global Poverty and the New Tuberculosis, Verso, London, 39-54.
- 15. Williams, D.R. and Collins, C. (2001) Racial Residential Segregation: A Fundamental Cause of Racial Disparities in Health. Public Health Reports, 116, 404-416.
http://dx.doi.org/10.1016/S0033-3549(04)50068-7 - 16. Reitmanova, S., and Gustafson, D.L. (2012) Coloring the White Plague: A Syndemic Approach to Immigrant Tuberculosis in Canada. Ethnicity & Health, 17, 403-418.
http://dx.doi.org/10.1080/13557858.2011.645156 - 17. Schluter, P., Ford, R., Mitchell, E. and Taylor, B. (1997) Housing and Sudden Infant Death Syndrome. The New Zealand Cot Death Study Group. The New Zealand Medical Journal, 110, 243-246.
- 18. Torrey, E.F. and Yolken, R.H. (1998) Is Household Crowding a Risk Factor for Schizophrenia and Bipolar Disorder? Schizophrenia Bulletin, 24, 321.
- 19. Shmool, J.L., Kubzansky, L.D., Newman, O.D., Spengler, J., Shepard, P. and Clougherty, J.E. (2014) Social Stressors and Air Pollution across New York City Communities: A Spatial Approach for Assessing Correlations among Multiple Exposures. Environmental Health, 13, 91. http://dx.doi.org/10.1186/1476-069X-13-91
- 20. Tunstall, H., Mitchell, R., Gibbs, J., Platt, S. and Dorling, D. (2011) Socio-Demographic Diversity and Unexplained Variation in Death Rates among the Most Deprived Parliamentary Constituencies in Britain. Journal of Public Health, 34, 296-304.
- 21. Adeboyejo, A.T. and Onyeonoru, I. (2003) Residential Density and Adolescent Reproductive Health Problems in Ibadan, Nigeria. African Population Studies, 18, 81-95.
- 22. Dhonte, P., Bhattacharya, R. and Yousef, T. (2000) Demographic Transition in the Middle East-Implications for Growth, Employment, and Housing. International Monetary Fund, No. 0-41.
- 23. Al-Habees, M.A. (2012) Determination of the Residential Housing Needs Expected for Cities of Jordan Within the Period of (2014-2024). Management Science and Engineering, 6, 130-139.
- 24. Baker, M.G., Goodyear, R., Telfar Barnard, L. and Howden-Chapman, P. (2006) The Distribution of Household Crowding in New Zealand: An Analysis Based on 1991 to 2006 Census Data: Wellington.
- 25. Olmos, J.C.C. and Garrido, á.A. (2007) African immigrants in Almeria (Spain): Spatial Segregation, Residential Conditions and Housing Segmentation. Sociologia, 39, 535-559.
- 26. Haan, M. (2011) The Residential Crowding of Immigrants in Canada, 1971-2001. Journal of Ethnic and Migration Studies, 37, 443-465. http://dx.doi.org/10.1080/1369183X.2011.526772
- 27. Khalifa, M.A. (2011) Redefining Slums in Egypt: Unplanned versus Unsafe Areas. Habitat International, 35, 40-49. http://dx.doi.org/10.1016/j.habitatint.2010.03.004
- 28. Mohamed, N.S., Nofal, L.M., Hassan, M. and Elkaffas, S. (2003) Geographic Information Systems (GIS) Analysis of under Five Mortality in Alexandria. The Journal of the Egyptian Public Health Association, 79, 243-262.
- 29. Ryan, T.P. (2008) Modern Regression Methods. Vol. 655, John Wiley & Sons, Hoboken.
- 30. Chatterjee, S. and Hadi, A.S. (2013) Regression Analysis by Example. John Wiley & Sons, Hoboken.
- 31. Montgomery, D.C., Peck, E.A. and Vining, G.G. (2012) Introduction to Linear Regression Analysis. Vol. 821, John Wiley & Sons, Hoboken.
- 32. Fotheringham, S., Charlton, M. and Brunsdon, C. (1998) Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environment and Planning A, 30, 1905-1927. http://dx.doi.org/10.1068/a301905
- 33. Brunsdon, C., Fotheringham, A.S. and Charlton, M. (2008) Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. In: Kemp, K., Ed., Encyclopedia of Geographic Information Science, Sage Publication, California, 558.
- 34. Charlton, M., Fotheringham, S. and Brunsdon, C. (2009) Geographically Weighted Regression. White Paper. National Centre for Geocomputation, National University of Ireland Maynooth, 1-14.











