Journal of Geographic Information System
Vol.6 No.4(2014), Article ID:48677,13 pages
DOI:10.4236/jgis.2014.64029
Calculate Thermal Infrared Intensity of the Hull’s Military Ship
Ramin Ebrahimi Laleh1, Nima Ghasemloo2
1Navigation Department, ShenavariJvad-Alaaemeh College NEDSA, Imam Hossin University, Tehran, Iran
2National Cartographic Center of Iran, Tehran, Iran
Email: Nima.ghasemloo@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2014; revised 10 June 2014; accepted 5 July 2014
ABSTRACT
Stealth technology emphasizes on the reduction in reflection and radiation energies, the surface of target's body in the range of visual, radar, thermal and near IR and so on. Providing solutions to reduce thermal IR intensity radiation is one of the appropriate actions in passive defense for identifying power and targeting enemy. Therefore, questions are brought up: How much is the thermal IR intensity radiation of surface of the hall’s vessel? How much is the effect of each parameter? This thesis tries to provide the software to answer these questions. The provided software measures thermal IR intensity radiation of the surface of the hall’s vessel by the material substance, the temperature of the surface of the hall’s vessel, the situation and characteristic of the thermal detector, noticing the coefficient of environment atmospheric transmittal. This software by changing the effective parameters on thermal IR radiation calculates the thermal radiation on thermal detector in different situations.
Keywords: Intensity Radiation, Thermal Infrared, Thermal Detector, Geometry’s Military Ship Neural

1. Introduction
One of the passive defense measures for ships (vessels) is reducing or eliminating the identifiable symptoms for military sensors that caused concealment and camouflage for military vessels. Identifiable symptoms depend on the type of identifier sensor of enemy. Thus for the passive defense measures, it is necessary to determine the level of identifiable symptoms [1] [2] .
1.1. Thermal Sensors
Thermal sensors as passive receivers, undertakes the task of detecting targets that have different thermal radiation from their background and work at thermal infrared spectrum on the two bands 3 - 5 and 8 - 14 micrometers (with respect to the thermal of vessel’s hull surface), and detect the target by differentiation the thermal radiation target from background [3] .
1.2. Infrared Radiations of a Vessel
Thermal infrared radiations of a vessel are divided into two categories:
1) Thermal radiation due to the inner heat of vessel: which arises from the action of mechanical and electronic equipment such as main and auxiliary vessel’s engine, vessel’s kitchen, location of staffs, and other activities that it’s heat is driven out of the vessel by vessel’s air conditioning systems and chimneys [4] [5] , that is not the desired of this paper.
2) Thermal radiation of vessel’s hull surface, which arises from heating by sources outside the vessel such as sun and environment [4] -[7] . In this paper, we are going to computation thermal radiation intensity of vessel’s hull surface.
In this research, affecting parameters for thermal infrared radiation are derived from various sources and books [3] [6] , and by computer coding succeeded in obtain a computational algorithm of thermal infrared radiation of vessel’s hull surface for thermal sensor in various positions around the vessel.
Similar research is designed and developed by the scientific centers of countries such as Belgium, Canada and other leading countries in science and technology, such as OSMOSIS software, but due to military applications, it is not available [2] . Milewski et al. in 2012 discuss selected methods of modification of vessel’s infrared signature and effectiveness of infrared camouflage. Theoretical analyses were preceded by experimental measurements. The measurement-class infrared cameras and imaging spectroradiometers were used in order to determine the radiant existence from different surface types [4] . Davis et al. in 2002 show how various simulation techniques can be used to design and specify subsystems that affect the ultimate IR signature of a vehicle. These subsystems can then be specified in detail for the construction of the platform [5] . Schleijpen in 2010 presents a set of simulation tools which can be used for assessing the effectiveness of these measures. The toolset consists of a chain of models which calculate the infrared signature of a ship (EOSM), generate an infrared image of the ship in a realistic sea and sky background (EOSTAR) and determine the behavior of an infrared missile seeker against these images and simulate the complete missile fly-out including countermeasure deployment (EWM) [8] .
The ultimate goal of this research is to reduce the thermal infrared radiation of vessel’s hull, that to achieve this goal we need the appropriate software for computer simulation of thermal infrared radiation levels of vessel’s hull. Thus effective parameters of this software must be introduced and proper equations are considered for computation these parameters. Also by accurate identification of the involved parameters in thermal infrared radiations, the proper method can be offered to reduce radiation.
2. Thermal Infrared Radiation
Heat transfer between warm phenomena and the surroundings is done by three methods including conduction, convention and radiation. Conductivity and convention heat transfer requires changing the temperature in materials, but radiation heat transfer does not require the material. The purpose of thermal radiation is radiant energy that radiates from bodies due to their temperature. At temperatures above the absolute zero, all bodies will emit thermal radiation [6] .
Thermal radiation is also specified as a part of the electromagnetic spectrum that has a wavelength of 0.1 to 100 micrometers, because the radiation emitted by bodies due to their temperature often occurs completely in this wavelength range. Thus, thermal radiation includes fully visible radiation and part of infrared and part of the ultraviolet radiations [6] [9] .
The energy emitted from bodies is important for us just due to their temperature. Electrons, atoms and molecules of all solids, liquids and gases with temperatures above zero move constantly, so with the same quality that have absorption and transmission in the entire volume of the material, constantly radiate, namely radiation is a volume phenomenon.
However, for solid opaque (no transmission), such as metals, wood and rocks, radiation is considered a surface phenomenon, Because the radiation emitted from the inner layer never reaches to the surface and incoming radiation to this bodies are usually absorbed by a surface layer of a few microns. Radiation properties of surfaces can be completely changed by using the thin layers coverage on them [10] .
In order to extract road from satellite image, methods are usually depending upon the spatial resolution and sensor characteristics. In these images, roads are shown as thin lines in low resolution while in high resolution image; roads appear as homogeneous area [7] . There are different methods for image classification where neural network is one of the frequently used methods in this regard in this research, the image is classified through neural network and is divided into two categories (i.e., road and non road). In what follows, classification by neural networks method is discussed briefly.
3. The Equations on Thermal Radiation Intensity
3.1. Black Body
Black body is used as a standard basis to compare the radiation properties of real surfaces. A blackbody is defined as fully absorptive and diffuser of radiation [11] [12] .
3.2. Radiated Power
Stefan Boltzmann law: in 1884 proved that the radiation of a black body is as follows:
![]() (1)
(1)
In this equation, the emission of thermal radiation is proportional to the fourth
power of the absolute temperature, and
![]() is a constant [11] [12] .
is a constant [11] [12] .
Planck’s diffusion law: Stefan Boltzmann law gives power of general emission of
black body Eb, which is the sum of the emitted radiation at all of wavelengths.
Sometimes we need to know the spectrum emission power of black body, which is the
amount of radiation energy emitted by a black body at the absolute temperature T
per second, per surface, and per wavelength units within the range of wavelength![]() .
.
A relation is presented in 1901 by Max Planck for spectrum emission of black body Ebλ, which is in connection with his quantum theory. This relation is known as the Planck diffusion law and is expressed as follows [11] [12] :
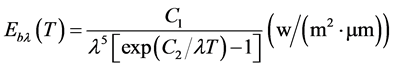 (2)
(2)
C1 and C2 are constant and T is temperature in terms of Kelvin
(temperature of +273 in terms of ˚C) and
![]() is wavelength of corresponding temperature.
is wavelength of corresponding temperature.
The maximum wavelength of the radiation is calculated by the Wien displacement law. This relation is essentially expressed by Wiley in 1894 using classical thermodynamics [11] [12] .
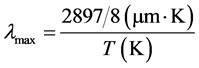 (3)
(3)
Emission coefficient of a surface is defined as the ratio of emitted radiation by
a surface to emitted radiation by a black body at the same temperature. Emission
coefficient of a surface is shown by
 and it varies from 0 to 1
and it varies from 0 to 1![]() . Emission coefficient shows similarity of
a surface for approximation it with blackbody
. Emission coefficient shows similarity of
a surface for approximation it with blackbody
![]() [11]
[12] .
[11]
[12] .
Thermal radiation intensity means the amount of thermal energy radiated of surface unit (for example a square meter) perpendicular to the strike of propagation, with a wavelength proportional to surface temperature. Thus radiation intensity is a volume property that calculates by the following equation [11] [12] .
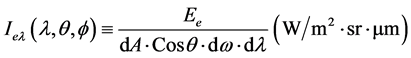 (4)
(4)
In the above equation,
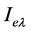 is the thermal radiation intensity with specified wavelength
angle vertex and azimuth, and Ee is emission power of thermal radiation
of an actual surface with specified wavelength divided by area dA, angle of observation
of desired surface
is the thermal radiation intensity with specified wavelength
angle vertex and azimuth, and Ee is emission power of thermal radiation
of an actual surface with specified wavelength divided by area dA, angle of observation
of desired surface
![]() along the spatial angle
along the spatial angle
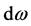 at the range of single wavelength
at the range of single wavelength . Unit of spectrum radiation intensity
. Unit of spectrum radiation intensity
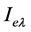 is in terms of
is in terms of![]() .
.
In the above equation, emission power of actual body with single wavelength and
directions of
![]() can be written as:
can be written as:
![]() (5)
(5)
where the unit of
![]() is
is![]() . In figure 1
. In figure 1
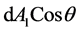 is actually area
is actually area
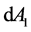 from the view of
from the view of
![]() [11]
[12] .
[11]
[12] .
4. Material and Methods
Computer simulation is used for modeling, computation and various analyzes. Simulation provides the possibility of modeling the actual vessel to computations be carried out on the model and desired analysis be obtained.
In this study, to modeling computation of the thermal infrared radiation of a vessel’s hull, computer simulation technique is used to obtain the thermal infrared radiation intensity of desired vessel’s hull with determined specification and position, and thereby carried out proper analysis for measuring and reducing thermal infrared radiation level.
figure 2 has stated procedures of computing thermal infrared radiation of vessel’s hull.
4.1. Drawing Geometry Vessel
In this project 3D MAX software was used that have proper capabilities, and after hull’s geometric drawing, hull’s surface was divided into triangle meshes. The more number of hull’s surface meshes, increases accuracy of drawing body’s geometry but by increasing the meshes number, number and time of computations also increases; so powerful computers will be required to perform the computations.
The use of geometric information is possible if can be convert geometric information of vessel’s hull into numerical data. This data contains the coordinates of the vessel’s hull that effects computation of area and normal vector of small surfaces of vessel’s hull and other computations (figure 3).
4.2. Data Transfer to Computational Software
Vessel’s geometric data that is extracted with “object” output format from geometric software should be useable in Arc GIS software. So required editing is performed on the mentioned data to be useable (figure 4).
4.3. Programming in VBA in ARCGIS
After data entry in ARC MAP, existing data should be used now for computation thermal radiation intensity. The aim of this project is to determine thermal infrared radiation intensity of vessel’s hull towards the thermal sensor with defined location and properties of thermal sensor. So equation (4) is used for thermal radiation intensity computation (figure 5).
We also use Planck’s diffusion law to calculate thermal infrared radiation power and use Wien’s displacement law to calculate the maximum wavelength.
4.4. Issue Assumptions
1) Temperature is considered constant.
2) Hull’ surface is considered isothermal.
3) Temperature changes due to convention is considered zero that means vessel’s static.
4) The wavelength used: maximum wavelength based on hull’s surface temperature.
5) Gender of entire hull’s surface is considered equal, thus problem has a same emission coefficient for entire vessel’s surface and this value can be changed.
6) Sensor’s surface area and location of thermal sensor is adjustable and their value can be changed.
7) Atmospheric transmittance coefficient is considered one that means full transmission of thermal radiation.
8) Normal vector of thermal sensor’s surface is in strike of origin of coordinates.
4.5. Entry the Required Information
In this program, two states are considered to measure radiation. In the first state it is assumed that sensor is located at a specific distance of vessel and rotates around it, radiation level for any vessel is calculated 45 degree.
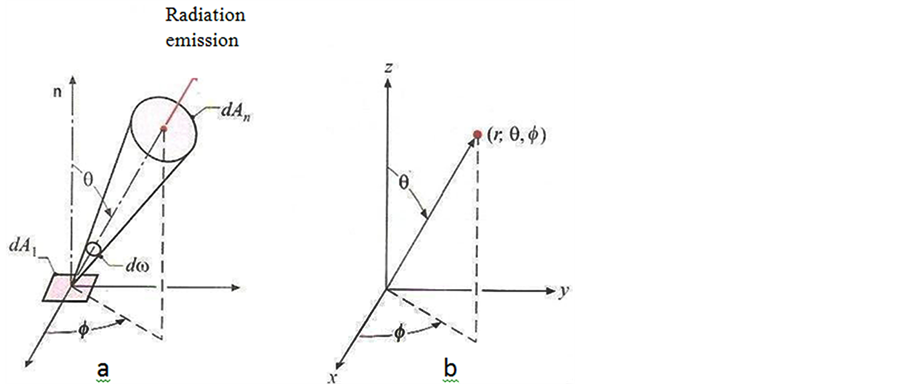
Figure 1. Directional nature of radiation. (a) Radiation
emission from differential surface dA1 on the differential surface dAn
under spatial angle![]() ; (b) Spherical coordinates system.
; (b) Spherical coordinates system.

Figure 2. Procedures of computing thermal infrared radiation of vessel’s hull.
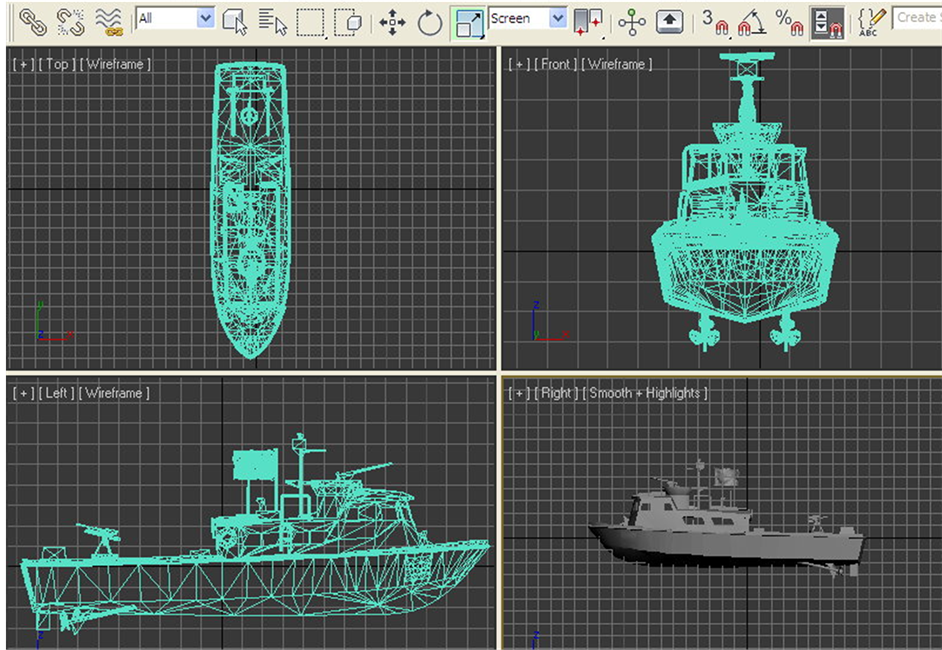
Figure 3. Geometry of floating body.

Figure 4. Import geometry of floating body to ARC MAP.
The required information includes sensor’s distance to vessel and sensor’s height, and average coordinates of X, Y, Z to measure distance of this point. For this purpose, it is assumed that in the second state, sensor is located
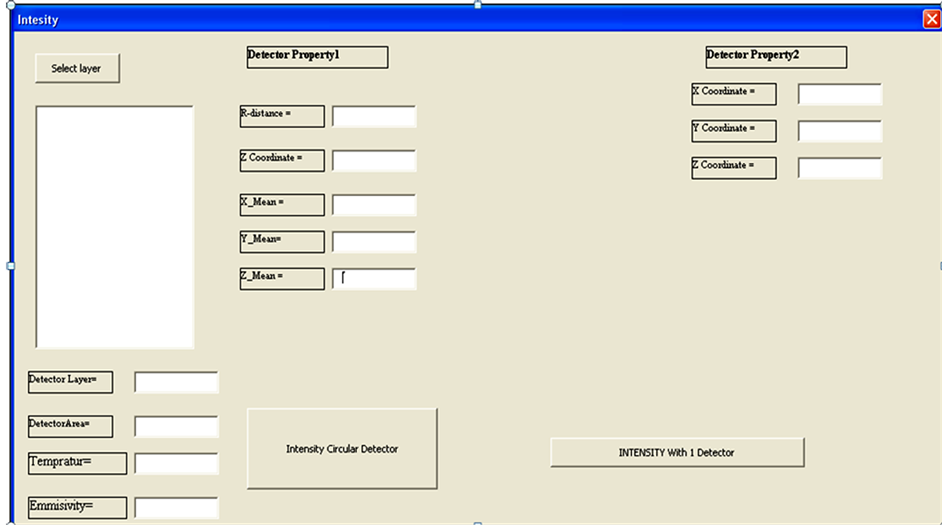
Figure 5. VBA programming for computation thermal radiation intensity.
in specific location and it is sufficient to entry the information of coordinates of X, Y, Z to calculate radiation level of it (figure 6).
There is a possibility of a three dimensional view of the vessel and thermal sensors.
To obtain thermal infrared radiation intensity received to the thermal sensor, sum of the radiation intensity of the surfaces is obtained.
5. Presentation and Analysis of the Results for a Vessel’s Hull
The results obtained from simulation of thermal infrared radiation for vessel’s hull is computed for patrol vessel with a length of 20 m, width of 5.5 m, height of vessel’s floor of 6 m and draught of 2.1 m that is shown in figure 7. Distance of thermal sensor of 300 m and height of 30 m from center of vessel’s coordinates, with emission coefficient of 0.03 for polished aluminum surface and temperature of 300 Kelvin and locating of thermal sensor clockwise at eight points of vessel’s bow with distance of 45 degree of vessel’s bow is computed and shown.
5.1. Effect of Sight Coefficient of Hull’s Surfaces
According to figure 7, it is shown that sight coefficient of vessel’s hull surfaces is very effective in radiation power, so that when the sensor locates at vessel’s bow (angle of 0 or 360 degree), with respect to the lower sight coefficient of hull’s surface, it receives the least radiation power, and when the sensor locates at both vessel’s sides (90 or 270 degree from vessel’s bow), due to increasing the sight coefficient of hull’s surface, received radiation intensity is also increases .
5.2. Effect of Hull’s Surface Temperature
Increasing the hull’s surface temperature of vessel causes the shorter wavelengths, but increases thermal radiation intensity of vessel’s hull surface.
In figure 8, three different temperatures of 295, 300 and 305 Kelvin is considered for vessel’s hull surface, and other parameters have been assumed identical. The obtained results implies an increase in thermal infrared radiation of vessel’s hull surface, which this increase is not linear, but is sinusoidal that is due to increasing the sight coefficient of vessel’s hull at its sides.
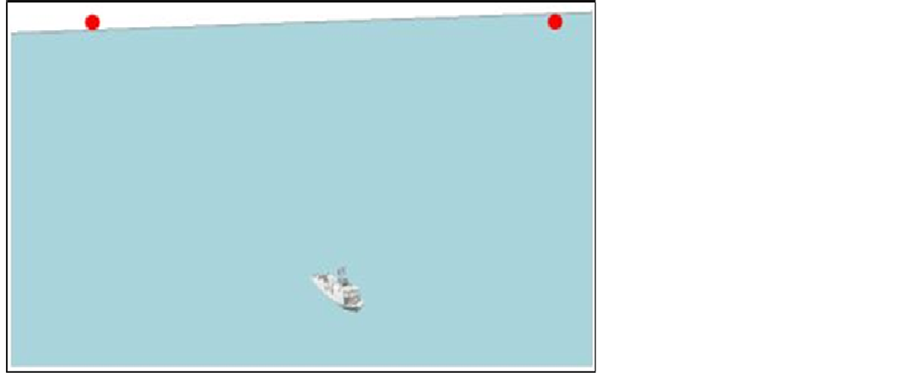
Figure 6. Three dimensional views of the vessel and thermal sensorsin ARC Scene.
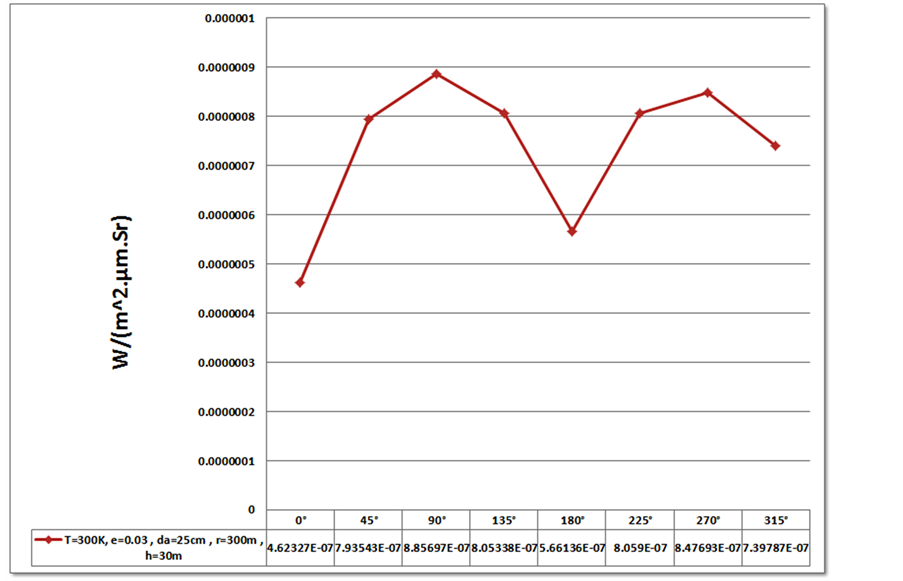
Figure 7. The results obtained from simulation of thermal infrared radiation for vessel’s hull.
5.3. Effect of Emission Coefficient of Hull’s Surface
Hull’s surface emission coefficient is very impressive in calculation of thermal infrared radiation intensity, so that the rate of changes in hull’s surface emission coefficient can be seen in figure 9. In this example, same emission coefficient is used for entire vessel’s hull surface, whereas in actual vessel, emission coefficient changes for different parts of vessel’s hull with respect to the properties of different materials used in the vessel’s hull and variety of colors and even corrosion of hull.
In figure 9 changes of thermal infrared radiation for different emission coefficients of vessel’s hull surface is seen, that include polished aluminum surface with emission coefficient of 0.03, Anode aluminum surface with emission coefficient of 0.84, white color of the hull’s surface with emission coefficient of 0.92, and black color
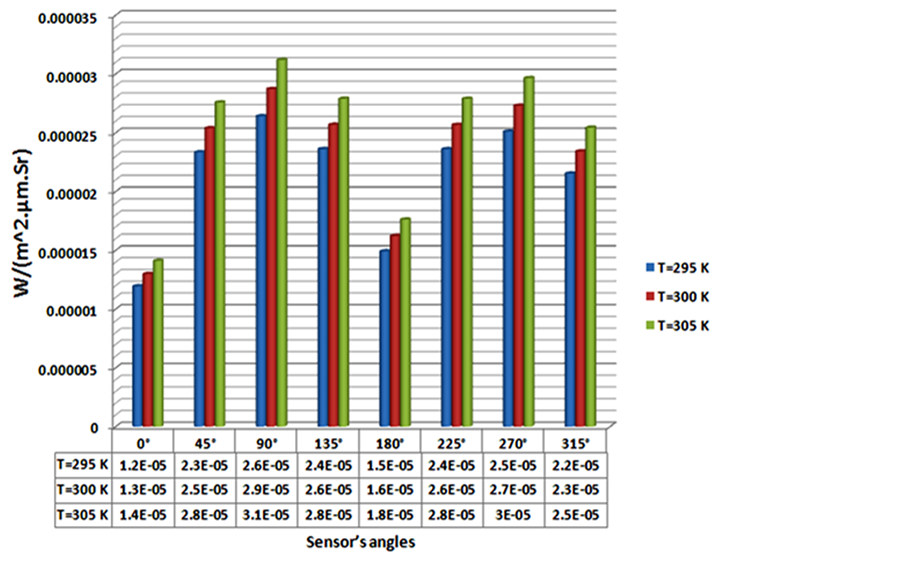
Figure 8. Difference in radiation intensity between several temperatures of the surface of the floating body.
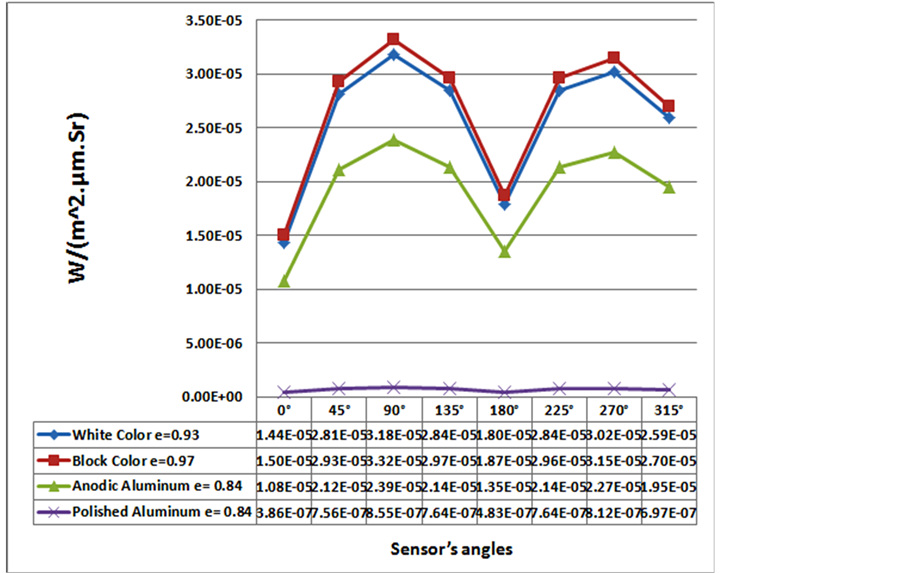
Figure 9. Radiation intensity in terms of several emissivity coefficients.
of the hull’s surface with emission coefficient of 0.97, that causes thermal infrared radiation intensity of vessel’s hull.
5.4. Effect of Surface Area of Thermal Sensor
One of the effective parameters in the amount of the received radiation to thermal sensor is ocular surface area of the thermal sensor, and in figure 10 two thermal sensors with different areas is shown.
In the above diagram, difference of thermal infrared radiation intensity received to thermal sensor with surface area of 25 and 30 cm2 is shown. This diagram shows that increasing in ocular surface area of thermal sensor increases the amount of thermal infrared radiation intensity received to the sensor.
5.5. Effect of Sensor’s Distance from Vessel on Thermal Infrared Radiation Intensity
The effect of thermal sensor distance from vessel’s hull is shown in figure 11, which the amount of thermal infrared radiation intensity reduces with increasing vessel’s distance from surface of vessel’s hull, and with reducing this distance, the amount of thermal infrared radiation intensity received by sensor increases.
In figure 11, there is an inverse relation between the distance of sensor from vessel and the amount of thermal infrared radiation intensity received by sensor. In the above diagram, at a constant angle of 72 degree that the distance values includes 240, 270, 300 and 330 meters, the amounts of thermal infrared radiation intensity reduces with increasing the distance.
5.6. Effect of Position of Thermal Sensor
Coordinates and position of thermal sensor is effective in the amount of thermal infrared radiation intensity received to the thermal sensor, and figure 12 shows the amount of thermal infrared radiation intensity received by the thermal sensor in different positions with keep the distance and change in elevation of thermal sensor.
The above diagram concludes that the position of thermal sensor from hull’s surface of vessel affects the amount of received power of the thermal sensor; and thermal sensor receives several of thermal infrared radiation intensity in different positions.
6. The Results of Computer Simulations
1) To obtain thermal infrared radiation intensity of vessel’s hull, computation the radiation intensity of any element of the hull’s surface of the vessel is required.
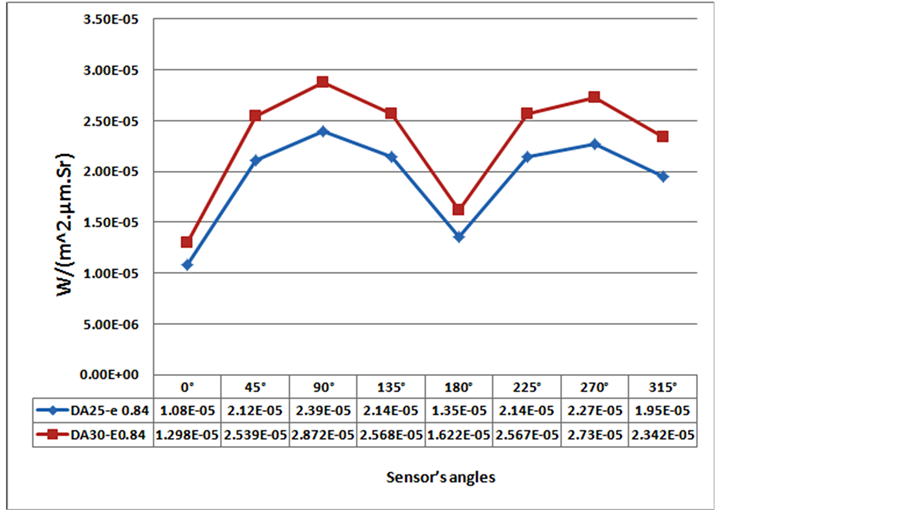
Figure 10. Impact of the area of the surface of the sensor on the radiation intensity received by the sensor.
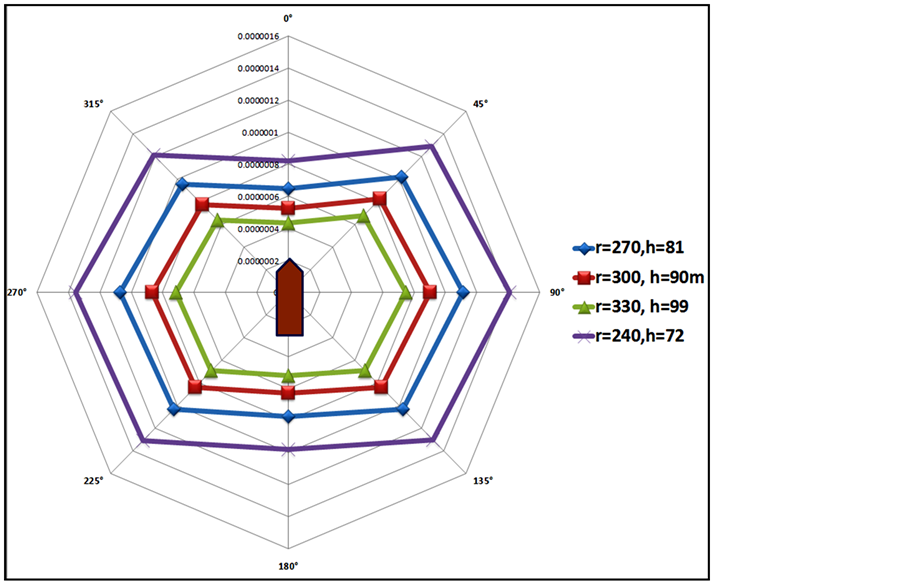
Figure 11. Amount of thermal infrared radiation intensity received by sensor in different distance of sensor from vessel.
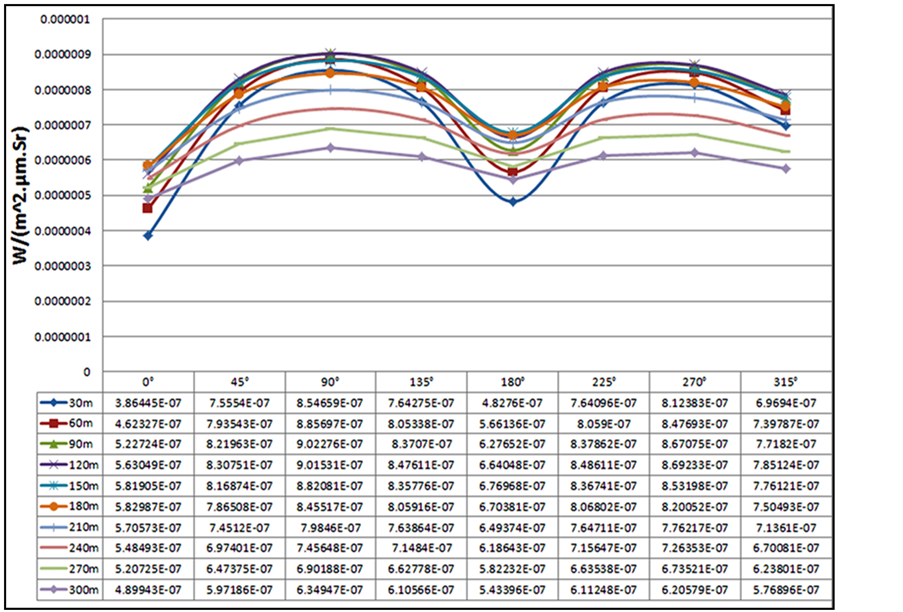
Figure 12. 360-Deg thermalinfraredradiation intensity of the floating body at the distance of 300 meters with several heights.
2) Area of the element surface and its normal vector is effective in computation of thermal radiation and should be computed.
3) Geometry of the vessel’s hull is effective in the level of thermal infrared radiation intensity, and the received thermal infrared radiation intensity increases with the amount of surfaces normal to the thermal sensor.
4) By increasing the area of vessel’s hull surfaces, thermal infrared radiation intensity also increases.
5) Position of the thermal sensor is effective in sight coefficients of vessel and causes changes in the received thermal infrared radiation intensity.
6) The gender of hull’s surface (emission coefficient) is effective in thermal infrared radiation intensity, and by approaching the emission coefficient to one, the received radiation power approaches to maximum value.
7) The surface normal of sensor and area of ocular surface should be computed to be used in equation of sight coefficient of the thermal sensor.
8) The area of sensor’s surface is effective in thermal infrared radiation and have a direct relation with it, so that by increasing the area of sensor’s surface, the received thermal infrared radiation intensity increases.
9) The amount of received intensity in the normal surface vector of thermal sensor is the maximum value and by increasing the angle of the received power reduces in proportion to the angle.
10) The distance of thermal sensor from hull’s surface of vessel has an inverse relation with the amount of thermal infrared radiation intensity, so that with increasing the distance, the amount of thermal infrared radiation intensity reduces.
11) Transmission coefficient of atmosphere is effective in the received thermal infrared radiation intensity, so that when transmission coefficient of atmosphere approaches to one, maximum power is received by the sensor.
12) Radiation power of vessel’s surface that usually have 8 - 12 micrometers wavelength, has not the ability to transmit from the atmosphere, thus this type of sensors should be placed below the atmosphere.
13) Atmosphere attenuation factor for 8 - 12 micrometers wavelength is mainly water vapor in the air, so humid air is effective in thermal infrared radiation attenuation.
7. The Proposed Methods for Reducing Thermal Infrared Radiation of Vessel’s Hull
1) Isolating the temperature created within the vessel’s hull.
2) Wet down the vessel’s surface by vessel’s firefighting systems for being isothermal vessel’s hull surface with the background (seawater).
3) Cooling the vessel’s hull surface by water tubes that passed from the surface of vessel’s hull.
4) The use of water vapor around the vessel to cause attenuation the atmospheric transmission.
5) Insert the vessel in proper shelter away from the solar thermal radiation.
6) Use of materials with low absorption and emission coefficient.
7) Use of the hull color with low absorption and emission coefficient.
8) Guiding the exhaust of vessel towards the sea water.
9) Mobility and displacement of vessel to cool the surface of vessel’s hull by moving the air around it.
10) Miniaturization the design of the surface of vessel’s hull.
11) Use of the curved surfaces in the surface of vessel.
8. Conclusions
Thermal infrared sensors have the ability to identify the targets on the base of temperature difference between the body and the background. To calculate the number of these radiations, heat thermal transfer equations are used. Heat transfer equations are computable in terms of both spectrum and geometry.
1) Spectrum depends on the temperature of the body’s surface, the created wavelength, the amount of environmental atmospheric attenuation, and operating wavelength of the sensor.
2) Geometry depends on the number of target surfaces, area of any target surface, normal vector of any surface, position of sensor around the target, distance of sensor from target, surface area of sensor, and normal vector of sensor surface.
References
- Milewski, S., Dulski, R., Kastek, M., Trzaskawka, P., Barela, J. and Firmanty, K. (2011) Coatings Masking in Near, Medium and Far-Infrared Used for Ship Camouflage. Proceedings of SPIE, 8185. http://dx.doi.org/10.1117/12.898293
- Lapierrea, F.D., Marcela, J.-P. and Acheroya, M. (2006) Design of an Infrared Ship Signature Simulation Software for General Emissivity Profiles. Electrical Engineering Department (SIC), Brussels.
- Budzier, H. and Gerlach, G. (2010) Thermal Infrared Sensors: Theory, Optimisation and Practice. Wiley, Hoboken.
- Milewski, S., et al. (2012) Modification of Infrared Signature of Naval Vessels. SPIE Defense, Security, and Sensing. International Society for Optics and Photonics, 8355.
- Davis, W.R. and Thompson, J. (2002) Developing an IR Signature Specification for Military Platforms Using Modern Simulation Techniques. SMi Conference: Pursuit of Stealth, London.
- Wooster, M. (2013) Thermal Infrared Remote Sensing: Sensors, Methods, Applications. In: Kuenzer, C. and Dech, S., Eds., Thermal Infrared Remote Sensing (Remote Sensing and Digital Image Processing, 17), Springer, Berlin, 43-67.
- Casscells, S.W., et al. (1999) Detecting Thermal Discrepancies in Vessel Walls. US Patent No. 5935075.
- Schleijpen Ric, H.M.A. (2010) Toolset for Evaluating Infrared Countermeasures and Signature Reduction for Ships. Security+ Defence. International Society for Optics and Photonics, 7836.
- Weng, Q.H. (2009) Thermal Infrared Remote Sensing for Urban Climate and Environmental Studies: Methods, Applications, and Trends. ISPRS Journal of Photogrammetry and Remote Sensing, 64, 335-344. http://dx.doi.org/10.1016/j.isprsjprs.2009.03.007
- McAtee, B.K., Prata, A.J. and Lynch, M.J. (2003) The Angular Behavior of Emitted Thermal Infrared Radiation (8-12 μm) at a Semiarid Site. Journal of Applied Meteorology, 42, 1060-1071. http://dx.doi.org/10.1175/1520-0450(2003)042<1060:TABOET>2.0.CO;2
- Siegel, R. (2002) Thermal Radiation Heat Transfer. Taylor & Francis, Taylor.
- Iqbal, M. (1983) An Introduction to Solar Radiation. Access Online via Elsevier.

