Natural Science
Vol.08 No.02(2016), Article ID:63630,4 pages
10.4236/ns.2016.82008
An Independence Property for General Information
Doretta Vivona, Maria Divari
Department of Basic and Applied Sciences for Engineering, Faculty of Civil and Industrial Engineering, “Sapienza”―University of Rome, Roma, Italy

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 December 2015; accepted 19 February 2016; published 22 February 2016
ABSTRACT
The aim of this paper was a generalization of independence property proposed by J. Kampé de Feriét and B. Forte in Information Theory without probability, called general information. Therefore, its application to fuzzy sets has been presented.
Keywords:
Information, Functional Equations, Fuzzy Sets

1. Introduction
Since 1967-69, J. Kampé de Ferét and B. Forte have introduced, by axiomatic way, new information measures without probability [1] - [3] ; later, in analogous way, with P. Benvenuti we have defined information measures without probability or fuzzy measure [4] for fuzzy sets [5] [6] . This form of information measure is again called general information.
In Information Theory an important role has played by an independence property with respect to a given information measures J applied to crisp sets [7] . These sets are called J-independent (i.e. independent each other with the respect to J) [8] .
For this reason we will propose a generalization of J-independence property.
The paper develops in the following way: in Section 2 we recall some preliminaires; in Section 3 the generalization of J-indepedence is proposed; the result is extended to fuzzy sets in Section 4. Section 5 is devoted to the conclusion.
2. Preliminaires
Let  be an abstract space and
be an abstract space and  the s-algebra of crisp sets
the s-algebra of crisp sets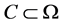 , such that
, such that 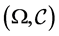 is a measurable space. We refer to [7] for all knoledge and operations among crisp sets.
is a measurable space. We refer to [7] for all knoledge and operations among crisp sets.
J. Kampé de Ferét and B. Forte gave the following definition [1] [2] :
Definition 2.1 Measure of general information J for crisp sets is a mapping
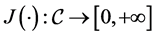
such that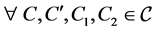 :
:
(i) 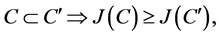
(ii) 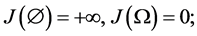
(iii) 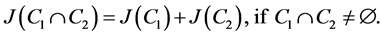
If the couple 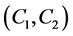 satisfies the (iii), we say that
satisfies the (iii), we say that 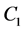 and
and 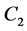 are J-independent, i.e. independent each other with respect to information J.
are J-independent, i.e. independent each other with respect to information J.
3. A Generalization of the J-Independence Property
In this paragraph we are going to present a generalization of the J-independence property.
We propose the following:
Definition 3.1 Given a general information J, let  and
and  be two crisp sets in C such that
be two crisp sets in C such that 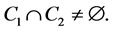 We say that
We say that 



We shall characterize the function

Putting 
We can give the following
Proposition 3.2 A class of solutions of the system [(P1) - (P5)] is

where h is any continuous, strictly increasing function 

Proof. The class of functions (2) satisfy the equations [(P1)-(P3)] and the inequality (P4) by appling the Ling Theorem about the representation of a function which is monotone, commutative, associative with neutral element [11] . The inequality (P5) is a consequence of the monotonicity of h.
So, from (2), we have
Proposition 3.3 The generalization of the J-independence property for crisp sets is

where h is any continuous, strictly increasing function 


Remark When h is linear, the generalization (3) coincide with the property (iii).
4. Extension to Fuzzy Setting
In this paragraph, we are considering the extension of J-independence property at fuzzy setting.
Let 


Definition 4.1 Measure of general information in fuzzy setting is a mapping 

(i')
(ii')
(iii')
If the couple 



Also in fuzzy setting, we generalize the (iii'), setting

The properties of the intersection between fuzzy sets are the similar to the [(p1) − (p4)] [5] [6] . Therefore, we are looking for functions (4) solutions of the system [(P1) − (P5)]. We have again the similar result:
Proposition 4.2 A class of solution of the system [(P1) − (P5)] is

where k is any continuous, strictly increasing function 

From (5), we get
Proposition 4.3 A generalization of the J'-independence property between two fuzzy set is

where k is any continuous, strictly increasing function 

Proof. The proof is similar to that given for crisp sets.
Remark. When k is linear, the generalization (6) coincide with the property (iii').
5. Conclusions
In this paper we have proposed a genralization of J-independence property between crisp sets:
where h is any continuous, strictly increasing function 

Therefore, we have extended the result to fuzzy setting:
where k is any continuous, strictly increasing function 

Cite this paper
DorettaVivona,MariaDivari, (2016) An Independence Property for General Information. Natural Science,08,66-69. doi: 10.4236/ns.2016.82008
References
- 1. Kampé de Fériet, J. and Forte, B. (1967) Information et Probabilité. Comptes Rendus de l’Académie des Sciences Paris, 265, 110-114, 142-146, 350-353.
- 2. Forte, B. (1969) Measures of Information: The General Axiomatic Theory. RAIRO Informatique Théorique et Applications, 63-90.
- 3. Kampé de Feriét, J. (1970) Mesures de l'information fornie par un evénement. Colloque International du Centre National de la Recherche Scientifique, 186, 191-221.
- 4. Benvenuti, P., Vivona, D. and Divari, M. (1990) A General Information for Fuzzy Sets. Uncertainty in Knowledge Bases, Lectures Notes in Computer Sciences, 521, 307-316. http://dx.doi.org/10.1007/BFb0028117
- 5. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- 6. Klir, G.J. and Folger, T.A. (1988) Fuzzy Sets, Uncertainty and Information. Prentice-Hall International Editions, Englewood Cliffs.
- 7. Halmos, P.R. (1965) Measure Theory. Van Nostrand Company, Princeton.
- 8. Benvenuti, P. (2004) L’opera scientifica. Roma, Ed.Univ.La Sapienza, Italia.
- 9. Aczél, J. (1966) Lectures on Functional Equations and Their Applications. Academic Press, New York.
- 10. Forte, B. (1970) Functional Equations in Generalized Information Theory. In: Applications of Functional Equations and Inequalities to Information Theory, Ed. Cremonese, Roma-Italy, 113-140.
- 11. Ling, C.-H. (1995) Representation of Associative Functions. Publicationes Mathematicae, 12, 189-212.
















