Natural Science Vol.07 No.01(2015), Article ID:53435,12 pages
10.4236/ns.2015.71005
The Classical Binary and Triplet Distribution Functions for Dilute Relativistic Plasma
N. A. Hussein1, D. A. Eisa2, E. G. Sayed1
1Mathematics Department, Faculty of Science, Assiut University, Assiut, Egypt
2Mathematics Department, Faculty of Science, Assiut University, New Valley, Egypt
Email: aragamal@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 January 2015; accepted 19 January 2015; published 22 January 2015
ABSTRACT
The aim of this paper is to calculate the binary and triplet distribution functions
for dilute relativistic plasma in terms of the thermal parameter
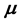 where
where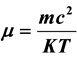 ,
,
 is the mass of charge;
is the mass of charge;
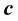 is the speed of light;
is the speed of light;
 is the Boltzmann’s constant;
and
is the Boltzmann’s constant;
and
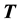 is the absolute temperature. Our calculations are based on the relativistic Bogoliubov-Born-Green-Kirkwood-Yvon
(BBGKY) hierarchy. We obtain classical binary and triplet distribution functions
for one- and two-component plasmas.
is the absolute temperature. Our calculations are based on the relativistic Bogoliubov-Born-Green-Kirkwood-Yvon
(BBGKY) hierarchy. We obtain classical binary and triplet distribution functions
for one- and two-component plasmas.
Keywords:
Relativistic Plasma, Binary and Triplet Distribution Functions, BBGKY Hierarchy

1. Introduction
Studying the properties of plasma has received a great interest in both astrophysical and laboratory plasma application. The relativistic binary distribution function is one of the most important functions of statistical mechanics. The importance of the distribution function in statistical mechanics is due to the fact that all the thermodynamic quantities, such as the pressure, the internal energy and the free energies, can be calculated from it.
Relativistic statistical mechanics has a long story, but we may notice that, whereas the theory of relativistic ideal gases has received deep and detailed developments, little has been achieved in order to account for mutual interactions between particles [1] . In statistical physics, the BBGKY hierarchy (Bogoliubov-Born-Green- Kirkwood-Yvon hierarchy, sometimes called Bogoliubov hierarchy) is a set of equations describing the dynamics of a system of a large number of interacting particles. The equation for an s-particle distribution function (probability density function) in the BBGKY hierarchy includes the -particle distribution function thus forming a coupled chain of equations [2] . Their history of 70 years has brought enormous progress in the investigation of the transition from the microscopic to the macroscopic world, and they are still an attractive starting point for new developments. In particular, great advance has come by clever methods of truncation, approxi- mation and scaling limits of the hierarchy, providing in various cases a justification of the kinetic equations describing particle systems on mesoscopic (intermediate) scales [3] . Many authors studied the BBGKY hierarchy [4] and [5] ; Hussein and Eisa [6] [7] calculated the binary and triplet distribution function for one- and two- component plasmas for quantum and classical non-relativistic plasma. In this paper, we will calculate these distributions in the relativistic case in terms of plasma thermal parameter. Arendt and Eilek [8] showed that the
pair-plasma distribution functions could be described by a thermal parameter
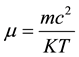 that was moderately
that was moderately
relativistic. The thermal parameter value plays a significant role for the stability of our system. Barcons and Lapiedra (1984) [9] gave explicit expressions for the thermodynamic functions of a high-temperature electron- positron plasma and gave expression for distribution functions for a classical dilute arbitrarily hot plasma in equilibrium which we compared our results with it.
Special relativity, however, does not permit velocities greater than the speed of
light
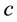 and is thus incompatible with a Maxwellian distribution that predicts a non-zero
probability for every velocity [10] . It is possible to obtain the relativistic
Maxwellian distribution (Jüttner distribution) of a moving gas when the so-called
Planck-Einstein case is analyzed. It should be reiterated that the Planck-Einstein
theory suffered a modification, principally in the transformation law of energy
(the Planck-Einstein case) [11] . Treumann et al. [12] have also shown that the
isotropic thermal equilibrium distribution function in relativistic plasma analytically
has the form of a modified Jüttner distribution.
and is thus incompatible with a Maxwellian distribution that predicts a non-zero
probability for every velocity [10] . It is possible to obtain the relativistic
Maxwellian distribution (Jüttner distribution) of a moving gas when the so-called
Planck-Einstein case is analyzed. It should be reiterated that the Planck-Einstein
theory suffered a modification, principally in the transformation law of energy
(the Planck-Einstein case) [11] . Treumann et al. [12] have also shown that the
isotropic thermal equilibrium distribution function in relativistic plasma analytically
has the form of a modified Jüttner distribution.
A little is known about relativistic distribution functions involving more than
two particles, and in particular about the three-particle (or triplet) distribution
function. This is of course due to the greater mathematical complexity of higher
order correlation functions, and to a lack of a direct link with experiment. Although
one can consider experimental determination of triplet distribution function from
triple elastic scattering similar to that of the binary distribution function, but
to our knowledge, the measurement of three-body correlation function requires the
knowledge of the positions of three particles at the same time which is technically
very demanding to obtain in 3D samples [13] ; this means that the experiment to
measure the triplet distribution function directly requires high precision so that
the multiple scattering can be differentiated from single scattering. Essentially,
one follows the phase-space trajectory of the system as it evolves in time, and
has thus the same amount of information as one obtains in a simulation. Similarly
the particle positions have measured in dusty plasmas [14] . Lapiedra et al. [15]
have undertaken an application of predictive methods to relativistic statistical
mechanics. Coulomb forces between point charges are purely repulsive and charges
approach very close to each other. Coulomb systems, such as plasma or electrolytes,
are made of charged particles interacting through Coulomb’s law. The simplest model
of a Coulomb system is the one-component plasma (OCP), also called jellium: an assembly
of identical point charges, embedded in a neutralizing uniform background of the
opposite sign. Here we consider the classical (i.e. non-quantum) equilibrium statistical
mechanics of the OCP. It is rather straightforward to calculate higher-order correlation
functions from the measured configurations. Moreover we study the model of two-component
plasma (TCP) i.e. neutral system of point like particles of positive and negative
charges such as electrons and ions. For the numerical calculation we restrict ourselves
to the case of (TCP) which anti-symmetric with respect to the charges
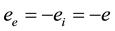 and therefore symmetrical with respect to the densities
and therefore symmetrical with respect to the densities . To simplify the numeric investigations, we simulated so far
only mass symmetrical electron-ion plasma with
. To simplify the numeric investigations, we simulated so far
only mass symmetrical electron-ion plasma with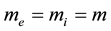 .
.
Homogeneous plasma is characterized by two parameters: the density of particles
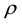 and the temperature
and the temperature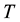 ;
if there are several kinds of particles, it is also necessary to state their concentrations.
There are different energies associated with the plasma, namely:
;
if there are several kinds of particles, it is also necessary to state their concentrations.
There are different energies associated with the plasma, namely:
1) Energy of the rest mass per particle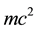 ;
;
2) Kinetic energy per particle of order ;
;
3) Coulomb energy of order

The ratios of these energies give us the two main dimensionless parameters of the plasma: the thermal para-
meter of plasma



are four different regimes characterized by it: plasma with




we note that the system is safely classical if where


is the typical linear momentum of particles. A relativistic plasma with a thermal distribution function has temperatures greater than around 260 keV, or 3.0 GK (5.5 billion degrees Fahrenheit), where approximately 10% of
the electrons have


astrophysics, including gamma-ray bursts, AGN jets, and pulsar winds. In physics,
a particle is called ultrarelativistic when its speed is very close to the speed
of light







In the astrophysical environment, the fraction of ionized particles varies widely from nearly no ionization in cold regions to fully ionized in regions of high temperature. This leads to a wide range of parameters where astrophysical plasmas can exist. While the astrophysical environment is frequently dominated by the presence of the plasma, this plasma is often strongly influenced by and coupled to the presence of embedded particulates (i.e., dust). These dust grains which range in size from a few nanometers to micron-sized objects can become either positively or negatively charged due to interactions with the background plasma environment and ionizing radiation sources in the astrophysical environment [16] . Understanding the processes that govern these plasma particle interactions is critical to the study of astrophysics. The agglomeration and growth of larger particles from single atoms and dust grains leads to the eventual formation of objects so large that gravity becomes the dominant force controlling their subsequent evolution [17] .
Another important point is that of the walls. We shall study plasma which is homogeneous
and isotropic but the plasma must be confined or it will expand. We may assume that
the plasma is confined by some kind of walls which prevent the escape of particles,
but that the container is so large that the effects of the walls are negligible.
Our calculations are based on the phase-space distribution function; this is defined
as the number of particles per unit volume of space per unit volume of velocity
space: At time t, number of particles in elementary volume of space, with velocities
in range
2. The Basic Equations and Hierarchy
The statistical state of a macroscopic system of N particles is in a complete―though in an intractably complex―
Figure 1. Qualitative sketch
of the four different regimes characterized by the thermal parameter μ and Lorentz
factor γ: our model lies in the region of high speeds, γ > 2 and
way described by the distribution function





tion of particle

The s-particle reduced distribution is giving by:

The relativistic BBGKY hierarchy [15] is given by

where



The Einstein summation convention is only valid for Greek labels. Therefore, for
each value of s we have s equations, since




According to what we done in non-relativistic case [7] we set, whatever particles 1, 2, 3 are,

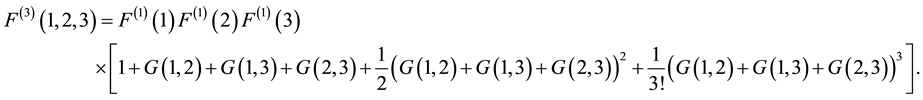
Let us consider the case of homogeneous plasma in equilibrium. Then



where

Figure 2. The one particle relativistic distribution function in the particle velocity interval (0, 0.9c) for different values of the thermal parameter μ.
3. The Binary Relativistic Distribution Function
At first sight, the calculation of the relativistic interaction between two charged
particles seems rather involved, because the force on particle 1 at time

To calculate the binary relativistic distribution function substituting from Equations
(3) and (5) into (2) for



Then, by solving the integro-differential Equation (7) and by using the Fourier transform of


generalized distribution function



Let us now study the two-particle relativistic distribution for the model of two-component
plasma (TCP) i.e. neutral system of point like particles of positive and negative
charges such as electrons and ions. For the numerical calculation we restrict ourselves
to the case of two-component plasma which anti-symmetric with respect to the charges


For two-component plasma we can use the two-particle correlation function



where


with







The standard two-body distribution function for dilute slightly relativistic plasma
has been calculated previously by Kosachev and Trubnikov [21] starting from the
Darwin Lagrangian. Lapiedra and Santos [19] result agrees with theirs to order

According to our knowledge few scientists studied the binary distribution function for relativistic dilute plasma [15] ; the new in our article is using effects of thermal parameter on the values of binary relativistic distribution function for one and two-component plasma.
4. The Triplet Relativistic Distribution Function
The triplet distribution function



Substituting Equation (4) and (5) into (2) for


If we used the Kirkwood superposition approximation (KSA) [23] ; which is consisting of the assumption that the potential in a set of three particles is the sum of the three pair potentials, this is equivalent to assuming that the triplet distribution function is the product of the three radial distribution functions

It has been mentioned that before 2003 there is no direct measurement of three-body correlation function and this is the first study for the triplet distribution function in the case of dilute relativistic plasma. Such measurement requires the knowledge of the positions of three particles at the same time which is technically very demanding to obtain in 3D samples [13] ; this means that the experiment to measure the triplet distribution function directly requires high precision so that the multiple scattering can be differentiated from single scattering. Now because of the existence of video-microscopy, a modern experimental technique applied to colloidal systems to directly measure all particles’ positions at all times. Essentially, one follows the phase-space trajectory of the system as it evolves in time, and has thus the same amount of information as one obtains in a simulation. Similarly the particle positions have measured in dusty plasmas [24] .
From Equation (12) we can obtain the classical TDF for two-component plasma in the following form:

And we also can used (KSA) which is given in Equation (13) to get it in the form

The triplet and quadruple distribution functions as well as binary distribution function must be incorporated for a more accurate and complete discussion of macroscopic equilibrium properties. A little is known about distribution functions involving more than two particles, and in particular about the three-particle (or triplet) distribution functions. This is of course due to the greater mathematical complexity of higher order correlation functions, and to a lack of a direct link with experiment [25] . And this is considered the first study for the triplet distribution functions for dilute relativistic plasma.
5. Conclusions
In many physical systems, the description of a plasma as a Coulomb system is sufficient to reproduce most of the properties of interest. If the system is cold enough, the mean velocities of the particles are much smaller than the speed of light, and the charges may be assumed to interact via the instantaneous Coulomb potential. However, at sufficiently high temperatures, this approximation is no longer valid, and the contributions of the relativistic effects (which include, apart from the trivial kinetic corrections and of course all the retardation effects) must be incorporated when studying the equilibrium properties of the system [26] .
In the classical (non-quantum) case, the systematic approach adopted here follows the traditional route of the relativistic Bogoliubov-Born-Green-Kirkwood-Yvon (BBGKY) hierarchy for the reduced distribution functions by formal density expansion. Interestingly, this study is the first to display the effect of thermal parameter of plasma in the classical binary and triplet distribution function. Also the triplet relativistic distribution function for dilute plasma was calculated from the relativistic BBGKY hierarchy. We used the results to obtain the analytical forms of the classical triplet distribution functions for one- and two-component plasmas.
In Figure 3 and Figure
4 we noticed that the value of both binary and triplet relativistic distribution
function increased when the

Our calculations are grounded in the classical relativistic statistical mechanics.
Plasma is non-degenerate. The system is not dense, so one may neglect the contributions
of higher order particle interactions. Figure 5
and Figure 6 show that the two- and three-particle
distribution functions have become concentrated to ever-smaller region of speed

Figure 3. The two-particle relativistic distribution function in the particle velocity interval (0, 0.9c) for one-compo- nent plasma.
Figure 4. The three-particle relativistic distribution function in the particle velocity interval (0, 0.9c) for one-compo- nent plasma for different values of μ, v1 = v2 = v3 = v.
Figure 5. The two-particle relativistic distribution function for two-component plasma in the particle velocity interval (−c, c) at μ = 1; μ = 0.3 and v1 ≠ v2.
Figure 8 and Figure 9
show that the two- and three-particle distribution functions in the thermal parameter
of plasma





Figure 6. The three-particle relativistic distribution function in the particle velocity interval (0, 0.9c) for one-compo- nent plasma for different values of μ; v1 = v2 = v3 = v.
Figure 7. The comparison between F(2) from our result and from Barcons and Lapiedra [9] for v = 0.86c and v = 0.9c.
Figure 8. The two-particle relativistic distribution function in the thermal parameter of plasma μ interval (0, 1) for one-component plasma for different values of speed, v = 0.8c, v = 0.86c, v = 0.9c.

Figure 10 shows the comparison between the three-particle relativistic distribution function from Equations (14) and (15). One of them is based on the Kirkwood superposition approximation (KSA) which is consisting of the assumption that the potential in a set of three particles is the sum of the three pair potentials. This is equivalent
Figure 9. The three-particle relativistic distribution function in the thermal parameter of plasma μ interval (0, 1) for one-component plasma for different values of speed, v = 0.8c, v = 0.86c, v = 0.9c.
Figure 10. The comparison between F(3) from Equation (14) and F(3) from (KSA) for two-component plasma for μ = 1; at v1 = v2 = v3 = v.
Figure 11. The two-particle relativistic distribution function in the particle velocity interval (−c, c) for μ > 1 (weakly relativistic case).
to assume that the triplet distribution function is the product of the three radial distribution functions, and the other form is calculated by using the relativistic BBGKY hierarchy.
Figure 12. The two-particle relativistic distribution function in the particle velocity interval (−c, c) for μ = 1 (relativistic case).
Figure 13. The two-particle relativistic distribution function in the particle velocity interval (−c, c) for μ > 1 (weakly relativistic case).
Figure 14. The three-particle relativistic distribution function in the particle velocity interval (−c, c) for μ = 1 (relativistic case).
Finally, we can note that from Figures 11-14, the distribution function has become
more concentrated to ever- smaller region of speed

References
- Droz-Vincent, P. (1997) Direct Interactions in Relativistic Statistical Mechanics. Foundations of Physics, 27, 363-387. http://dx.doi.org/10.1007/BF02550162
- Bogoliubov, N.N. (1946) Probleme der Dynamischen Theorie in der Statistischen Physik. Moskau.
- Simonella, S. (2011) BBGKY Hierarchy for Hard Sphere Systems. Ph.D. Dissertation, Sapienza University of Rome, Rome.
- Kraeft, W.D., Kremp, D. and Ebeling, W. (1986) Quantum Statistics of Charged Particle Systems. Akademie Verlag, Berlin. http://dx.doi.org/10.1007/978-1-4613-2159-0
- Kahlbaum, T. (1999) Density Expansions of the Reduced Distribution Functions and the Excess Free Energy for Plasma with Coulomb and Short-Range Interactions. Contributions to Plasma Physics, 39, 181-184. http://dx.doi.org/10.1002/ctpp.2150390144
- Hussein, N.A. and Eisa, D.A. (2011) The Quantum Equation of State of Fully Ionized Plasmas. Contributions to Plasma Physics, 51, 44-50. http://dx.doi.org/10.1002/ctpp.201110003
- Eisa, D.A. (2012) The Classical Binary and Triplet Distribution Functions for Two Component Plasma. Contributions to Plasma Physics, 52, 261-275. http://dx.doi.org/10.1002/ctpp.201100030
- Arendt Jr., P.N. and Eilek, J.A. (2000) The Pair Cascade in Strong and Weak Field Pulsars. Pulsar Astronomy―2000 and beyond, 202, 445-448.
- Barcons, X. and Lapiedra, R. (1985) Statistical Mechanics of Classical Dilute Relativistic Plasmas in Equilibrium. Journal of Physics A: Mathematical and General, 18, 271-285. http://dx.doi.org/10.1088/0305-4470/18/2/017
- Swisdak, M. (2013) The Generation of Random Variates from a Relativistic Maxwellian Distribution. Physics of Plasmas, 20, Article ID: 062110. http://dx.doi.org/10.1063/1.4812459
- Ares de Parga, G. and Lopez-Carrera, B. (2011) Relativistic Statistical Mechanics vs. Relativistic Thermodynamics. Entropy, 13, 1664-1693. http://dx.doi.org/10.3390/e13091664
- Treumann, R.A., Nakamura, R. and Baumjohann, W. (2011) A Model of So-Called “Zebra” Emissions in Solar Flare Radio Burst Continua. Annales Geophysicae, 29, 1673-1682. http://dx.doi.org/10.5194/angeo-29-1673-2011
- Sciortino, F. and Kob, W. (2001) Debye-Waller Factor of Liquid Silica: Theory and Simulation. Physical Review Letters, 86, 648-651. http://dx.doi.org/10.1103/PhysRevLett.86.648
- Rosenfeld, Y., Levesque, D. and Weis, J.J. (1990) Free-Energy Model for the Inhomogeneous Hard-Sphere Fluid Mixture: Triplet and Higher-Order Direct Correlation Functions in Dense Fluids. The Journal of Chemical Physics, 92, 6818-6832. http://dx.doi.org/10.1063/1.458268
- Lapiedra, R. and Santos, E. (1981) Classical Relativistic Statistical Mechanics: The Case of a Hot Dilute Plasma. Physical Review D, 1, 2181-2188. http://dx.doi.org/10.1103/PhysRevD.23.2181
- Alam, M.S., Masud, M.M. and Mamun, A.A. (2014) Effects of Two-Temperature Superthermal Electrons on Dust-Ion- Acoustic Solitary Waves and Double Layers in Dusty Plasmas. Astrophysics and Space Science, 349, 245-253. http://dx.doi.org/10.1007/s10509-013-1639-3
- Masud, M.M., Kundu, N.R. and Mamun, A.A. (2013) Obliquely Propagating Dust-Ion Acoustic Solitary Waves and Their Multidimensional Instabilities in Magnetized Dusty Plasmas with Bi-Maxwellian Electrons. Canadian Journal of Physics, 91, 530-536. http://dx.doi.org/10.1139/cjp-2012-0390
- Lazar, M., Stockem, A. and Schlickeiser, R. (2010) Towards a Relativistically Correct Characterization of Counterstreaming Plasmas. I. Distribution Functions. Open Plasma Physics Journal, 3, 138-147. http://dx.doi.org/10.2174/1876534301003010138
- Lapiedra, R. and Santos, E. (1983) Classical Dilute Relativistic Plasma in Equilibrium. Two-Particle Distribution Function. Physical Review A, 27, 422-430. http://dx.doi.org/10.1103/PhysRevA.27.422
- Turski, L.A. (1974) Pair Correlation Function for a System with Velocity-Dependent Interactions. Journal of Statistical Physics, 11, 1-16. http://dx.doi.org/10.1007/BF01019474
- Kosachev, V.V. and Trubnikov, B.A. (1969) Relativistic Corrections to the Distribution Functions of Particles in a High-Temperature Plasma. Nuclear Fusion, 9, 53-56. http://dx.doi.org/10.1088/0029-5515/9/1/006
- Bel, L., Salas, A. and Sanchez, J.M. (1973) Approximate Solutions of Predictive Relativistic Mechanics for the Electromagnetic Interaction. Physical Review D, 7, 1099-1106. http://dx.doi.org/10.1103/PhysRevD.7.1099
- Kirkwood, J.G. (1935) Statistical Mechanics of Fluid Mixtures. The Journal of Chemical Physics, 3, 300-313. http://dx.doi.org/10.1063/1.1749657
- Bonitz, M., Henning, C. and Block, D. (2010) Complex Plasmas: A Laboratory for Strong Correlations. Reports on Progress in Physics, 73, Article ID: 066501. http://dx.doi.org/10.1088/0034-4885/73/6/066501
- Barrat, J.L., Hansen, J.P. and Pastore, G. (1988) On the Equilibrium Structure of Dense Fluids: Triplet Correlations, Integral Equations and Freezing. Molecular Physics, 63, 747-767. http://dx.doi.org/10.1080/00268978800100541
- Kalman, G.J., Rommel, J.M., Blagoev, K. and Blagoev, K. (1998) Strongly Coupled Coulomb Systems. Springer, Berlin. http://www.springer.com/physics/particle+and+nuclear+physics/book/978-0-306-46031-9

















