Natural Science
Vol.06 No.10(2014), Article ID:46950,13 pages
10.4236/ns.2014.610072
Glycolytic Synchronization in Yeast Cells via ATP and Other Metabolites: Mathematical Analyses by Two-Dimensional Reaction-Diffusion Models
Hiroshi Serizawa, Takashi Amemiya, Kiminori Itoh
Graduate School of Environment and Information Sciences, Yokohama National University, Yokohama, Japan
Email: seri@qb3.so-net.ne.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2014; revised 20 May 2014; accepted 30 May 2014
ABSTRACT
Possibilities of synchronized oscillations in glycolysis mediated by various extracellular metabo- lites are investigated theoretically using two-dimensional reaction-diffusion systems, which ori- ginate from the existing seven-variable model. Our simulation results indicate the existence of al- ternative mediators such as ATP and 1,3-bisphosphoglycerate, in addition to already known ace- taldehyde or pyruvate. Further, it is also suggested that the alternative intercellular communica- tor plays a more important role in the respect that these can synchronize oscillations instanta- neously not only with difference phases but also with different periods. Relations between inter- cellular coupling and synchronization mechanisms are also analyzed and discussed by changing the values of parameters such as the diffusion coefficient and the cell density that can reflect in- tercellular coupling strength.
Keywords:
Acetaldehyde, ATP, Glycolytic Oscillation, Intercellular Coupling, Reaction-Diffusion Model, Synchronization

1. Introduction
Synchronization in biological systems is widely observed in the natural world. This phenomenon is one of the collective behaviors thought to have a crucial role in maintaining the individual life or in giving benefits for communities. One of the well-known examples is synchronized flashing of male fireflies [1] [2] .
Glycolysis is a biological mechanism to decompose glucose and to store energy in the form of ATP. In this chemical process, synchronized variations can be seen for the concentrations of various metabolites [3] - [8] . For example, yeast cells exhibit glycolytic synchronized oscillations under certain conditions. A suspension of yeast cells with high population densities shows synchronization, whereas that with low densities does not. The emer- gence of the collective behavior such as synchronization may occur above a critical cell density.
The theoretical studies of glycolytic oscillations in yeast cells using differential equations started substantially when Sel’kov presented a simple kinetic model of an enzyme reaction with substrate inhibition and product ac- tivation [9] . His ordinary differential equation system with two variables showed the occurrence of periodic self- oscillations in glycolysis. Another starting point is the allosteric enzyme model by Goldbeter and Lefever and Goldbeter, which also consists of two variables that referred to ATP and ADP, respectively [10] [11] . They adopted a partial differential equation system, which afterward facilitated a large extent of investigations for pattern formation and spatiotemporal structures. As these examples, we exemplify the studies of target pattern formation and spatiotemporal chaos by Zhang et al. [12] and of inward rotating spiral waves by Straube et al. [13] . Meanwhile, the Sel’kov model is succeeded by Lavlova et al. in the study of inward and outward wave propagation [14] . Besides these two streams, Bier et al. proposed a simple conceptual model consisting of glu- cose and ATP for explanation of glycolytic synchronized oscillations [15] .
The epoch-making study was performed by Wolf and Heinrich in order to elucidate the mechanisms of syn- chronous behaviors in glycolytic oscillations [16] . Based on the detailed description of glycolytic reaction processes, they constructed a seven-variable model, by which the effect of intercellular coupling on oscillatory dynamics was theoretically analyzed. Further, Henson et al. connected this model with the cell-ensemble model- ling technique and showed that a large ensemble of about 1000 population cells were required to adequately capture complex dynamic behaviors in glycolytic oscillations [17] .
However, it seems that no model has succeeded in demonstrating perfect synchronization of a large number of yeast cells that oscillated with different phases and periods. We guess that one of the reasons is that these mod- els assumed acetaldehyde or pyruvate to be an intercellular communication substance for glycolytic synchroni- zation.
It is known that acetaldehyde mediates the synchronization of glycolytic oscillations [6] . Various experiments demonstrated that acetaldehyde had a very strong synchronization effect on a suspension of yeast cells [8] . However, these studies do not exclude the possibility that extracellular nucleotides such as ATP and ADP can play an important role in synchronization of glycolytic oscillations in yeast cells. These are signaling molecules contained in all tissues [18] . Other studies also showed that Saccharomyces cerevisiae released ATP to extra- cellular solutions, suggesting that extracellular ATP, ADP, AMP or adenosine played a role in yeast physiology as intercellular communicators [19] [20] .
Then, we attempted to exchange acetaldehyde or pyruvate to ATP or other metabolites in the original model by Wolf and Heinrich [16] . Our present study using these modified seven-variable models shows that glycolytic synchronization in yeast cells may occur via intercellular mediators such as ATP and other metabolites, and that ATP is the most effective synchronizer even under the condition where individual cells have quite different properties.
2. Mathematical Models
Our mathematical models are derived from the glycolytic oscillation model originally presented by Wolf and Heinrich [16] . Major modifications are the following three:
1) Extension to two-dimensional partial differential equation systems with the diffusion term,
2) Exchange of the intercellular coupling substance and,
3) Non-dimensionalization for variables and parameters.
The first modification enables us to observe directly various kinds of oscillations including the synchronous one, and the possibilities of synchronization significantly increase by the second modification. Moreover, the third modification, which leads to the reduction of parameter numbers, eases mathematical analyses of simulation models.
The schematic diagram of the model is sketched in Figure 1, where the simulation area consists of N × N par- titioned square compartments divided at regular intervals. One cell is embedded within each compartment [16] [21] , whose volumetric ratio φ to the compartment is one of the key control parameters of our models. In this ar- ticle, we adopt N = 11 in all simulations, resulting in the total cell number is N × N (=121). However, the num- ber of N can be decided arbitrarily.
Six major substances are contained within a cell, which are denoted as S1, S2, S3, S4, N2 and A3. These are regarded as independent variables, the meanings of which are explained in Table 1. In addition to these six, two more substances, N1 and A2, are also contained, which are connected by the relations, N1 + N2 = N and A2 + A3 = A, respectively. As N and A are constant, two variables, N1 and A2, are not independent, whose numbers are auto- matically identified. In the original model, it is assumed that only S4 can permeate through the membrane, then, the substance in the external solution is labeled as 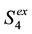 [16] . The model of this type, via the S4 intercellular me- diator, is also the starting point of our studies. The transmembrane coupling metabolite is later altered to the other one such as A3, S3, S2 and N2; thereafter, the variations of system behaviors are investigated.
[16] . The model of this type, via the S4 intercellular me- diator, is also the starting point of our studies. The transmembrane coupling metabolite is later altered to the other one such as A3, S3, S2 and N2; thereafter, the variations of system behaviors are investigated.
The meanings of parameters used in this article are also explained in Table 1, most of which are recycles of those in the original model [16] . The dimensionless parameter values are listed in Table 2, which are obtained by non-dimensionalization processes such as
Table 1. Variables and parameters in Models I, II, III, IV and V.
Most of variables and parameters were defined by Wolf and Heinrich [16] , which are reused in this article.

Figure 1. Schematic diagram of Models I, II, III, IV and V. (a) The simulation area is composed of N × N square compartments, in which a single glycolytic cell is embedded [16] [21] . In all simulations, the number of N is fixed at 11, thus, the total number of cells is N × N (=121). The temporal behaviors of five gray cells, one central cell plus four nearest neighbors, are selectively monitored in Figure 2, Figure 4 and Figure 5 (figures on the left side). (b) Each cell contains eight metabolites, S1, S2, S3, S4, N1, N2, A2 and A3, among which non-independent N1 and A2 are not shown. In Model I, the transmembrane substance is S4, whereas in Models II, III, IV and V, this is altered to A3, S3, S2 and N2, respectively. In- tercellular coupling metabolites diffuse through the boundary between adjacent compartments, which is expected to be feasible mechanisms to induce synchronized glycolytic oscillations. As for identification of S1, S2, S3, S4, N1, N2, A2 and A3, see Table 1.
Table 2. Parameter settings in Models I, II, III, IV and V.
Numerical analyses are performed using these parameter values. A parameter k7 is newly introduced for stabiliza- tion of the system. The diffusion coefficient dF and the parameter f0 that defines the amplitude of randomization are also employed. When f0 = 0.1, for example, randomized items such as initial values and parameter values are scattered within the range from 90% to 110% around the above values. As for two control parameters, φ and dF, two different values are provided in Model II, III and IV, while only dF is varied in Model I. Reference values are converted by non-dimensionalization procedures from those in the original model by Wolf and Heinrich [16] .
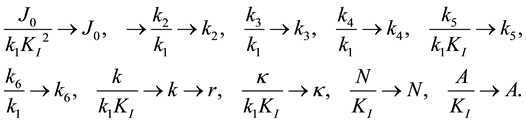
Two parameters, k1 and KI, are eliminated by these processes [21] . Besides, the original parameter k is renamed r, and a new parameter k7 is employed. The system is stabilized by the addition of k7, especially when the trans- membrane substance is changed to A3, S3, S2 or N2. As a result, our seven-variable, two-dimensional reac- tion-diffusion model with S4 being the intercellular mediator reads as follows.
 (1)
(1)
Here, the diffusion term is incorporated in the last equation, which describes the intercellular coupling via S4. This basic model described by Equations (1) is referred to as Model I in this article.
Next, we exchange the coupling substance in the external medium in order to examine other candidates that can produce synchronous oscillations. It should be noted that a new parameter k7 takes an important role as a stabilizer in these models. For example, when the substance that functions as the communicator is A3, the ma- thematical model is described such as
 (2)
(2)
To be accurate, one more variable A2 or 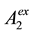 should be added besides
should be added besides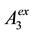 , however, it is confirmed that the addition of either variable hardly influences the simulation result. The system described by Equations (2) is re- ferred to as Model II in this article.
, however, it is confirmed that the addition of either variable hardly influences the simulation result. The system described by Equations (2) is re- ferred to as Model II in this article.
Similarly, we can construct the system with the intercellular communicator S3 (Equations (3)) and the system with the intercellular communicator S2 (Equations (4)). These are referred to as Model III and Model IV, respec- tively.
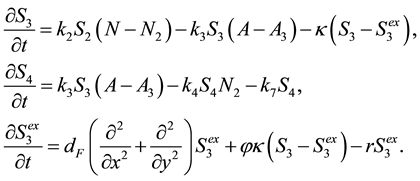 (3)
(3)
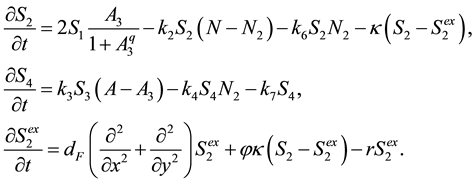 (4)
(4)
In above formulations of Equations (3) and Equations (4), several equations are omitted, which are the same as those in Equations (1). Moreover, we can construct Model V, where the intercellular mediator is N2, in the same manner, formulations of which are not shown explicitly.
Although two parameters are eliminated by non-dimensionalization procedures, there are still twelve parame- ters in our models except for two control parameters dF and φ. In principle, we try to use parameter values of the reference state converted from the original model [16] , which are listed in Table 2. If it is impossible to make stable limit cycle oscillations using these values, we adjust the values of such parameters as J0, r and κ, which are thought to be comparatively easy to manipulate. The exception is Model V, where the value of k5 is varied. Besides the reference [16] , the parameter values in the reference [17] are also referred to.
It is also important to choose properly the initial value of each variable. We determine these values in refer- ence to fixed points, which are calculated in advance. Table 3 is a list of initial values used to create synchron- ous oscillations. In the case of Model II, for example, the initial value of S1 is fluctuated within the range from 4.68 (= 5.2 × 0.9) to (5.72 = 5.2 × 1.1), S2 = 0.43 (= 4.3 × 0.1), and so on.
Table 3. Fixed points and initial values of variables corresponding to synchronous oscillations in Models I, II, III and IV.
“FP” denotes the fixed point. For detailed calculations, see Appendix.
3. Simulation Results
3.1. Synchronization and Desynchronization in Model I
Figure 2 displays the temporal changes in N2 concentrations from dimensionless time t = 7500 to t = 8000 in Model I, where the transmembrane metabolite is assumed to be S4, and only initial values of S1 are randomized within the fluctuation range from 75% to 125% around the main value. It should be noted that the perturbation of initial values causes the difference of phases only. Two figures (a) and (b) are the simulation results for dF = 1.0 and φ = 0.1, and (c) and (d) are those for dF = 0.01 and φ = 0.1. Meanwhile, (a) and (c) exhibit the temporal changes in central five cells, one central cell plus four nearest neighbors, and (b) and (d) do those in mean N2 concentrations for total 121 cells. In the case of dF = 1.0 and φ = 0.1, as shown in (a) and (b), the tightly syn- chronized oscillation is observed, which is strongly certified by the fact that wave patterns of five central cells are nearly overlapped and almost equal with the averaged one. In the case of dF = 0.01 and φ = 0.1, on the other hand, it seems that oscillations continue to be out of phase, as shown in (c), thus, Model I does not generate synchronous oscillations in this case.
The time series of two-dimensional distributions of N2 concentrations are illustrated in Figure 3. Upper three figures (a), (b) and (c) exhibit the synchronous oscillation, where dF = 1.0 and φ = 0.1, while lower three (d), (e) and (f) do the asynchronous oscillation, where dF = 0.01 and φ = 0.1. For each case, three drawing times are chosen so that the central cell at (5, 5) just passes the mean N2 value of the amplitude. Thus, they are slightly proceeded compared with the exact times, t = 2000, 4000 and 8000. As a result, it is confirmed that six central cells in Figure 3 are drawn by the same color. It should be noted that the synchronization processes in Model I advance comparatively at a slow pace.
We also examine the case where not only initial S1 values but also values of nine parameters, J0, k2, k3, k4, k5, k6, k7, r and κ, are randomized. In this case, oscillation periods are also disturbed as well as phases. However, it seems impossible to annihilate these differences, which leads to the conclusion that oscillations in Model I are asynchronous for randomization of both initial S1 values and nine parameter values, i.e., for disturbances of both oscillation phases and periods.
Assuming that the diffusion coefficient dF = ∞, our Model I corresponds exactly with the original model by Wolf and Heinrich [16] . However, the simulation results are not altered significantly compared with the case of
Figure 2. Temporal changes in N2 concentrations in Model I, t = 7500 - 8000. Two figures on the left side show the temporal changes of central five cells specified in Figure 1 (a), while two on the right side show those averaged for total 121 cells. (a) and (b) show the synchronous oscillation, where dF = 1.0 and φ = 0.1. Meanwhile, (c) and (d) show the asynchronous oscillation, where dF = 0.01 and φ = 0.1. In both cases, only initial values of S1 are randomized. Other parameter values are fixed in accordance with Table 2. It is recognized that the oscillations of five central cells are overlapped with each other, as shown in (a), and extremely similar with the averaged one, as shown in (b), indicating that almost all the cells oscillate with the same phases and periods.
Figure 3. Time series of two-dimensional distributions of N2 concentrations in Model I. Parameter settings are the same as those in Figure 2. (a), (b) and (c) show the evolution to the synchronous oscillation, where dF = 1.0, φ = 0.1 and (a) t~2000, (b) t~4000, (c) t~8000, respectively. Meanwhile, (d), (e) and (f) show the succession of the asynchronous oscillation, where dF = 0.01, φ = 0.1 and (d) t~2000, (e) t~4000, (f) t~8000, respectively. Elapsed time is slightly adjusted such that the central cell at (5, 5) takes the mean N2 value of the oscillation amplitude.
dF = 1.0, thus, we can expect almost the same results for simulations in the range of dF ≥ 1.0. These situations are also true for Models II, III, IV and V as well.
3.2. Synchronization and Desynchronization in Models II, III, IV and V
Despite almost complete synchronization for randomization of initial S1 values, we did not succeed in detecting any synchronous oscillation for randomization of parameter values. Then, we exchange the intercellular media- tor S4 to other substances in an attempt to synchronize oscillations with different periods.
Figure 4 exhibits the simulation results of Model II, where the transmembrane substance is A3, and both ini- tial S1 values and nine parameter values of J0, k2, k3, k4, k5, k6, k7, r, and κ are disturbed at the same time. Two figures (a) and (b) are the simulation results for dF = 1.0 and φ = 0.5, (c) and (d) are those for dF = 0.01and φ = 0.5 and (e) and (f) are those for dF = 1.0 and φ = 0.1, respectively. Meanwhile, three figures (a), (c) and (e) on the left side represent the temporal changes in central five cells, while (b), (d) and (f) on the right side do those in mean N2 concentrations for total cells. Different from the case of Model I, it is clear that the differences of both phases and periods disappear, and that synchronization occurs even for oscillations with different periods when dF = 1.0 and φ = 0.5, as shown in (a) and (b). Moreover, synchronization is fully completed until t~500, which is much faster than in Model I (Figure 2(a) and Figure 2(b)). However, oscillations continue to be asynchronous when dF = 0.01 and φ = 0.5, as shown in (c) and (d), and the system behavior results in the convergence to the fixed point when dF = 1.0 and φ = 0.1, as shown in (e) and (f).
Simulation results of Model III are also presented in Figure 5(a) and Figure 5(b), where the transmembrane substance is S3, and both initial S1 values and nine parameter values are simultaneously randomized. Temporal behaviors are also classified into three modes as well as in the case of Model II, namely, synchronous oscillations for dF = 1.0 and φ = 0.5 (Figure 5(a) and Figure 5(b)),asynchronous oscillations for dF = 0.01 and φ = 0.5 (not shown) and the convergence to the fixed point for dF = 1.0 and φ = 0.1 (not shown). Meanwhile in the case of Model IV, in which the coupling substance is S2, we confirmed no more than two modes of temporal beha- viors. These are synchronous oscillations for dF = 1.0 and φ = 0.5 (Figure 5(c) and Figure 5(d)), andasyn- chronous oscillations for dF = 0.01 and φ = 0.5 (not shown).
In the end, we examine Model V with the N2 intercellular mediator. Despite a large extent of surveys, we failed in finding any parameter set that realized synchronous oscillations. Figure 5(e) and Figure 5(f) exhibit one of the examples that display asynchronous oscillations. Both initial S1 values and nine parameter values are randomized as well as in Models II, III and IV. Needless to say, this does not necessarily exclude the possibility
Figure 4. Temporal changes in N2 concentrations in Model II. Three figures on the left side show the temporal changes of central five cells, while three on the right side show those averaged for all cells. (a) and (b) show the synchronous oscillation, where dF = 1.0, φ = 0.5 and t = 500 - 1000. Meanwhile, (c) and (d) show the asynchronous oscillation, where dF = 0.01, φ = 0.5 and t = 7500 - 8000. Further, (e) and (f) show the convergence to the fixed point, where dF = 1.0, φ = 0.1 and t = 7500 - 8000. The initial values of S1 and the values of nine parameters, J0, k2, k3, k4, k5, k6, k7, r, and κ, are simultaneously randomized. Other parameter values are fixed in accordance with Table 2. It should be noted that the oscilla- tions in Model II synchronize more rapidly, as shown in (a) and (b), compared with that in Model I (Figure 2).
that N2 is concerned with synchronization.
These simulation results in five models are summarized in Table 4. The oscillation period of Model II is ex- tremely short and almost half compared with those of other models.
4. Discussion
4.1. Two Levels of Synchronization
It seems to be two levels in synchronization of oscillations, namely, synchronization of phases and that of pe- riods. In general, perturbations of initial values cause merely phase shifts. Meanwhile, perturbations of parame- ter values are at least required to cause the difference of oscillation periods. Thus, it is likely that synchroniza- tion of different periods is more difficult and essential than that of phase differences. Taking this inference into consideration, we cannot say that synchronization is completed or perfect until oscillations become in phase even for randomization of parameters. In this sense, synchronization in Model I (Figure 2(a) and Figure 2(b)) via the S4 communicator is imperfect, while those of Models II (Figure 4(a) and Figure 4(b)), III (Figure 5(a) and Figure 5(b)) and IV (Figure 5(c) and Figure 5(d)) via the A3, S3 and S2 communicators are perfect.
Comparing three kinds of synchronization in Models II, III and IV, it seems that overlapping of oscillatory patterns in Model II is more outstanding than the other two. Thus, it could be speculated that synchronization via
Figure 5. Temporal changes in N2 concentrations in Models III, IV and V. Three figures on the left side show the temporal changes of central five cells, while three on the right side show those averaged for all cells. (a) and (b) show the synchronous oscillation in Model III, where dF = 1.0, φ = 0.5 and t = 500 - 1000. Moreover, (c) and (d) show the synchronous oscillation in Model IV, where dF = 1.0, φ = 0.5 and t = 500 - 1000. Meanwhile, (e) and (f) show the asynchronous oscil- lation in Model V, where dF = 1.0, φ = 0.5 and t = 7500 - 8000. The initial values of S1 and the values of nine parameters, J0, k2, k3, k4, k5, k6, k7, r, and κ, are simultaneously randomized. Other parameter values are fixed in accordance with Table 2.
Table 4. Correlations among transmembrane communicators, randomized items and oscillation modes.
Synchronous oscillations are observed for randomization of initial S1 values in Model I. Meanwhile in Models II, III and IV, syn- chronous oscillations can also take place for randomization of both initial S1 values and values of nine parameters J0, k2, k3, k4, k5, k6, k7, r and κ. However, any synchronous oscillation is not detected in Model V when N2 is an intercellular mediator. Dimensionless time periods corresponding to synchronous oscillations are listed for reference.
the A3 intercellular metabolite is the most perfect, indicating that the exchange of A3 is the most feasible me- chanism for glycolytic synchronization in yeast cells.
4.2. Quantification of Synchronization
In order to certify above inference numerically, the standard deviations of N2 concentrations are calculated for total 121 cells in Models II, III, IV and V, among which the former three are the synchronous cases and the last is the asynchronous case. The abscissae of Figures 6(a)-(d) are exactly the same as those of Figure 4(b), Fig- ure 5(b), Figure 5(d) and Figure 5(f), respectively. Standard deviations of N2 concentrations are divided by the mean value at each time for normalization, which guarantees the proper comparison between different models.
It is supposed that these normalized standard deviations reflect the degree of synchronization, and that the smaller value, the more perfect is synchronization. Among three synchronous cases in Figure 6, the values of Figure 6(a) are smaller than those of Figures 6(b) and 6(c), indicating that synchronization in Model II is more perfect than that in Model III or IV. This is the reason why we predict that A3 is the most probable metabolite in- volved in synchronous glycolytic oscillations in yeast cells.
Meanwhile, Figure 6(d) is the asynchronous case where normalized standard deviations keep high values. Moreover, any periodic structure is not detected, which is thought to be a typical characteristic of asynchronous oscillations.
4.3. Dependencies on Diffusion Coefficient and Cell Density
It is well known that glycolytic oscillations initiate synchronization under the densely populated condition [3] - [8] . Considering that high population densities mean intense coupling between cells, it is thought that collec- tive properties of synchronization in glycolytic oscillations is triggered by the increase in such parameters as the diffusion coefficient dF, the volumetric ratio of the cell to the compartment φ, the kinetic constant relating to the permeability κ, and so on. These are connected with such parameters as the compartment size L, the compart- ment volume V, the cellular surface area Ac, the cellular volume Vc and the permeability of the cellular mem- brane P, by the following relations [16] [21] .

Figure 6. Temporal changes in normalized standard deviations of N2 concentrations in Models II, III, IV and V. The standard deviations of N2 concentrations are divided by the mean value at each time. Four figures correspond to Figure 4(b), Figure 5(b), Figure 5(d) and Figure 5(f), respectively. These normalized standard deviations are introduced to estimate the degree of synchronization, and the smaller value means more perfect synchronization. It is clear that synchronization in Model II is the most perfect, as shown in (a), where A3 is the intercellular communicator. The last figure (d) shows the case of the asynchronous oscillation, where not only the values of standard deviations are high, but also no periodic structure is recognized.
In particular, we focus on dF and φ among these parameters in this article.
According to our simulation results of Models II, III and IV, the increase in dF gives rise to the transition from the asynchronous oscillation (for example, Figure 4(c) and Figure 4(d)) to the synchronous one (for example, Figure 4(a) and Figure 4(b)). This phenomenon can be called the Kuramoto transition [22] . On the other hand, the direct transition from the convergence to the fixed point (for example, Figure 4(e) and Figure 4(f)) to the synchronous oscillation (for example, Figure 4(a) and Figure 4(b)) is induced with the increase in φ in Models II and III. The characteristic of this phenomenon is that the shift to the synchronous oscillation proceeds directly without passing through the intermediate asynchronous oscillation. Thus, it could be speculated that the shifts to synchronization with the increases in the density parameter φ are due to mechanisms of the dynamical quorum sensing [23] -[25] .
5. Conclusions
1) Glycolytic oscillations with different phases can be synchronized by means of intercellular coupling via such substances as S4, A3, S3 and S2, as demonstrated in Models I, II, III and IV. Meanwhile, synchronization of oscillations with different periods can be mediated by intercellular coupling substances such as A3, S3 and S2, as demonstrated in Models II, III and IV. The latter synchronization is characterized by speedy convergence to the synchronous oscillatory state.
2) Among three candidates that can induce synchronization for different periods, A3 could be the most re- sponsible for the phenomenon, because the normalized standard deviations of N2 concentrations in Model II are the smallest compared with those in Model III or IV.
3) The transition from the asynchronous to the synchronous oscillation is observed with the increase in the diffusion coefficient dF, which could be referred to the Kuramoto transition mechanism. On the other hand, the direct transition from the convergence to the fixed point to the synchronous oscillation is observed with the in- crease in the density parameter φ, which could be referred to the dynamical quorum sensing.
Acknowledgements
We thank Drs. K. Shibata, P. G. Søensen, S. C. Müller, M. J. B. Hauser, T. Yamaguchi, T. Yamamoto and S. Sasaki for helpful discussion and M. Denda for giving us information on ATP as a signaling molecule.
References
- Buck, J. and Buck, E. (1968) Mechanism of Rhythmic Synchronous Flashing of Fireflies. Fireflies of Southeast Asia May Use Anticipatory Time-Measuring in Synchronizing Their Flashing. Science, 159, 1319-1327. http://dx.doi.org/10.1126/science.159.3821.1319
- Ramírez Ávila, G.M., Deneubourg, J.-L., Guisset, J.-L., Wessel, N. and Kurths, J. (2011) Firefly Courtship as the Basis of the Synchronization-Response Principle. Europhysics Letters, 94, Article ID: 60007. http://dx.doi.org/10.1209/0295-5075/94/60007
- Betz, A. and Chance, B. (1965) Phase Relationship of Glycolytic Intermediates in Yeast Cells with Oscillatory Meta- bolic Control. Archives of Biochemistry and Biophysics, 109, 585-594.
- Hess, B. and Boiteux, A. (1968) Mechanism of Glycolytic Oscillation in Yeast. I. Aerobic and Anaerobic Growth Conditions for Obtaining Glycolytic Oscillation. Hoppe-Seyler’s Zeitschriftfürphysiologische Chemie, 349, 1567-1574. http://dx.doi.org/10.1515/bchm2.1968.349.2.1567
- Aon, M.A., Cortassa, S., Westerhoff, H.V. and van Dam, K. (1992) Synchrony and Mutual Stimulation of Yeast Cells during Fast Glycolytic Oscillations. Journal of General Microbiology, 138, 2219-2227.
- Richard, P., Bakker, B.M., Teusink, B., van Dam, K. and Westerhoff, H.V. (1996) Acetaldehyde Mediatesthe Syn- chronization of Sustained Glycolytic Oscillations in Populations of Yeast Cells. European Journal of Biochemistry, 235, 238-241. http://dx.doi.org/10.1111/j.1432-1033.1996.00238.x
- Richard, P. (2003) The Rhythm of Yeast. FEMS Microbiology Reviews, 27, 547-557. http://dx.doi.org/10.1016/S0168-6445(03)00065-2
- Danø, S., Madsen, M.F. and Sørensen, P.G. (2007) Quantitative Characterization of Cell Synchronization in Yeast. Proceedings of the National Academy of Sciences of the United States of America, 104, 12732-12736. http://dx.doi.org/10.1073/pnas.0702560104
- Sel’kov, E.E. (1968) Self-Oscillations in Glycolysis. 1. A Simple Kinetic Model. European Journal of Biochemistry, 4, 79-86.
- Goldbeter, A. and Lefever, R. (1972) Dissipative Structures for an Allosteric Model. Application to Glycolytic Oscilla- tions. Biophysical Journal, 12, 1302-1315. http://dx.doi.org/10.1016/S0006-3495(72)86164-2
- Goldbeter, A. (1973) Patterns of Spatiotemporal Organizationin an Allosteric Enzyme Model. Proceedings of the Na- tional Academy of Sciences of the United States of America, 70, 3255-3259. http://dx.doi.org/10.1073/pnas.70.11.3255
- Zhang, L., Gao, Q., Wang, Q. and Zhang, X. (2007) Simple and Complex Spatiotemporal Structures in a Glycolytic Allosteric Enzyme Model. Biophysical Chemistry, 125, 112-116. http://dx.doi.org/10.1016/j.bpc.2006.07.004
- Straube, R., Vermeer, S., Nicola, E.M. and Mair, T. (2010) Inward Rotating Spiral Waves in Glycolysis. Biophysical- Journal, 99, L04-L06. http://dx.doi.org/10.1016/j.bpj.2010.04.018
- Lavrova, A.I., Bagyan, S., Mair, T., Hauser, M.J.B. and Schimansky-Geier, L. (2009) Modeling of Glycolytic Wave Propagation in an Open Spatial Reactor with Inhomogeneous Substrate Influx. BioSystems, 97, 127-133. http://dx.doi.org/10.1016/j.biosystems.2009.04.005
- Bier, M., Bakker, B.M. and Westerhoff, H.V. (2000) How Yeast Cells Synchronize Their Glycolytic Oscillations: A Perturbation Analytic Treatment. Biophysical Journal, 78, 1087-1093. http://dx.doi.org/10.1016/S0006-3495(00)76667-7
- Wolf, J. and Heinrich, R. (2000) Effect of Cellular Interaction on Glycolytic Oscillation in Yeast: A Theoretical Inves- tigation. Biochemical Journal, 345, 321-334. http://dx.doi.org/10.1042/0264-6021:3450321
- Henson, M.A., Müller, D. and Reuss, M. (2002) Cell Population Modelling of Yeast Glycolytic Oscillations. Biochemi- cal Journal, 368, 433-466. http://dx.doi.org/10.1042/BJ20021051
- Zhong, X., Malhotra, R. and Guidotti, G. (2003) ATP Uptake in the Golgi and Extracellular Release Require Mcd4 Protein and the Vacuolar H+-ATPase. Journal of Biological Chemistry, 278, 33436-33444. http://dx.doi.org/10.1074/jbc.M305785200
- Boyum, R. and Guidotti, G. (1997) Glucose-Dependent, cAMP-Mediated ATP Efflux from Saccharomyces Cerevisiae. Microbiology, 143, 1901-1908. http://dx.doi.org/10.1099/00221287-143-6-1901
- Jakubowski, H. and Goldman, E. (1988) Evidence for Cooperation between Cells during Sporulation of the Yeast Sac- charomyces cerevisiae. Molecular andCellularBiology, 8, 5166-5178.
- Schütze, J., Mair, T., Hauser, M.J.B., Falcke, M. and Wolf, J. (2011) Metabolic Synchronization by Traveling Waves in Yeast Cell Layers. Biophysical Journal, 100, 809-813. http://dx.doi.org/10.1016/j.bpj.2010.12.3704
- Weber, A., Prokazov, Y., Zuschratter, W. and Hauser, M.J.B. (2012) Desynchronisation of Glycolytic Oscillations in Yeast Cell Populations. PLoS ONE, 7, Article ID: e43276.
- De Monte, S., d’Ovidio, F., Danø, S. and Sørensen, P.G. (2007) Dynamical Quorum Sensing: Population Density En- codedin Cellular Dynamics. Proceedings of the National Academy of Sciences of the United States of America, 104, 18377-18381. http://dx.doi.org/10.1073/pnas.0706089104
- Tinsley, M.R., Taylor, A.F., Huang, Z. and Showalter, K. (2009) Emergence of Collective Behavior in Groups of Ex- citable Catalyst-Loaded Particles: Spatiotemporal Dynamical Quorum Sensing. Physical Review Letters, 102, Article ID: 158301. http://dx.doi.org/10.1103/PhysRevLett.102.158301
- Taylor, A.F., Tinsley, M.R., Wang, F., Huang, Z. and Showalter, K. (2009) Dynamical Quorum Sensing and Synchro- nization in Large Populations of Chemical Oscillators. Science, 323, 614-617. http://dx.doi.org/10.1126/science.1166253
Appendix
Calculations of Fixed Point
It is useful to know in advance the coordinates of fixed points for estimations of the initial values in numerical simulations. Fixed points are the solutions of the simultaneous equations in which all time derivatives equal zero. As for the fixed point of Model I, N2 is calculated by solving the quadratic equation for the first time, then, those of S2, S4, 

Here, the diffusion term is neglected.
For another example, the fixed point of Model II is computed, as follows.

Similarly, we can identify the coordinates of fixed points for Models III, IV and V as well. We would like to stress that coordinates of fixed points for each parameter value are calculated or identified precisely in all models presented in this article.







