Natural Science
Vol.4 No.3(2012), Article ID:18070,5 pages DOI:10.4236/ns.2012.43026
Two-photon excitation for C2V molecules based on the full relativistic theory wang#t1:sp——Characteristic symmetry for Cwang#_s:sub2Vwang#_e:sub groupwang#t1:ep
![]()
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu, China; zhuxm@scu.edu.cn
Received 10 December 2011; revised 11 January 2012; accepted 22 January 2012
Keywords: Two-photon excitation; C2v group; The full relativistic quantum mechanical theory
ABSTRACT
The present work explores a new phenomenon that not all the transition probability of two photon processes is negligible at low irradiance. The irreducible representation 2B2 of C2v is unexpected, for there is no much deviation in oscillator strength for two-photon and single-photon process A1 to 2B2. This new phenomenon is only possible to be explored by the symmetrical consideration: the necessary and sufficient condition is molecular plane coincident with yz plane or the operation  ##Bracket#(yz) for group C2v. It is only possible to be evaluated out by use of the full relativistic quantum mechanical theory.
##Bracket#(yz) for group C2v. It is only possible to be evaluated out by use of the full relativistic quantum mechanical theory.
1. INTRODUCTION
Since two-photon absorption had been theoretically described by Maria Göppert-Mayer as early as in 1931, the multiphoton process has been one of the most interested focuses after laser sources and synchrotron radiation.Two-photon absorption has been widely exploited in different fields due to its quadratic dependence on the irradiance, which makes it possible to confine the laser excitation to the focal volume. Such feature has led to a large number of technological applications, such as multiphoton fluorescence microscopy and two-photon photopolymerization.
The water molecule with only 10 electrons is an ideal system for comparing theory and experiment [1]. The process 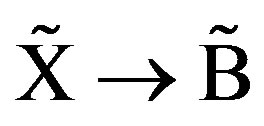 of H2O system has been excited by use of 266 nm two-photon excitation energy of 7.5186 eV.
of H2O system has been excited by use of 266 nm two-photon excitation energy of 7.5186 eV.
However, some of theoretical methods of two-photon absorption spectra were determined based on the density functional theory (DFT) with B3LYP functional as implemented at the Gaussian 03 package [2]. This is a nonrelativistic theory. It is better to use the full relativistic theory which is involved in both space and time symmetry [3]. The inclusion of inversion with the spatial rotation as a symmetry operation suggests through the relativistic equivalence of space and time that we also include a time-reversal operation, which is related with 4-dimensional Minkowski space. Time-reversal symmetry is introduced in Atomic and Molecular reaction Statics in 1996 [4].
Both furan (C4H4O) and molecule CHe2++ are the C2V symmetry. All the carbon, hydrogen and oxygen atoms of furan form a planar ring with 2pπ delocalization. It is necessary to explore its two photon processes and related with fluorescence. Molecule CHe2++ is one of possible species to solidify the α-particle emitted from plutonium atom, which is the most significant. It is to prove that there are no much deviation in the oscillator strength for single-photon and two-photon process A1 to 1B2 of group C2V.
2. THE FULL RELATIVISTIC THEORY
Symmetry plays an important role for quantum mechanical theory. There are three levels for quantum mechanical method: Non-relativistic based on the single point group, relativistic based on the double group and relativistic based on the full symmetry group or quarternion symmetry.
In consideration of the equivalence of space and time, for the relativistic theory based on the full symmetry group or quaternion symmetry, the time reversal symmetry operation is included in the symmetry group. It is well known that the product of two symmetry operators is represented by the product of the corresponding unitary matrices in the theory of group representation, however, time reversal symmetry operation is an antiunitary operator. The inclusion both of space and time operations, the group is called the full symmetry group, and their group representation is called a co-representation, this nomenclature is introduced by Wigner. The co-representation is not unitary representation; however, it is still possible to be broken down to irreducible form. The third level, i.e., relativistic quantum mechanical theory based on the full symmetry group or quaternion symmetry is firstly applied by the work of T. Saue and the others [5].
Time reversal operator or called Kramer operator [4] is defined as follows
 (1)
(1)
If Hamiltonian  is a real function of r, then
is a real function of r, then
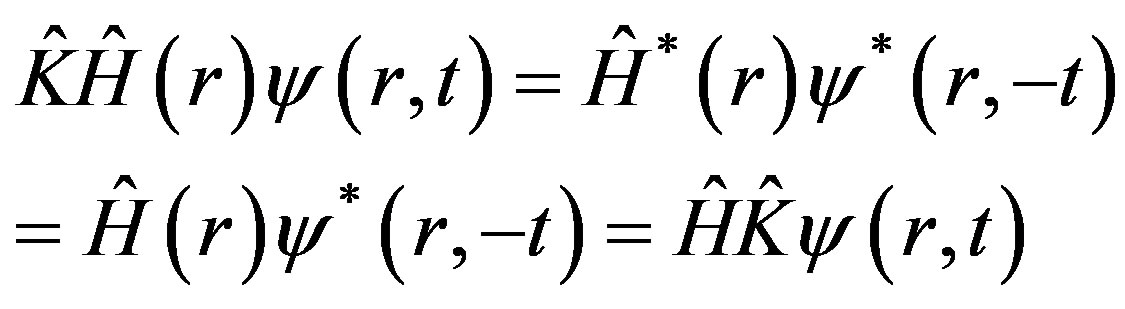 (2)
(2)
i.e.
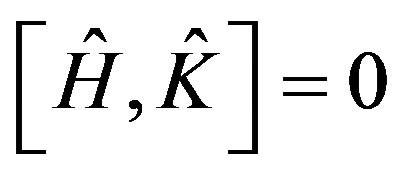 (3)
(3)
The commutator (3) is the necessary and sufficient condition for two operators 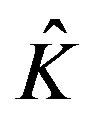 and
and 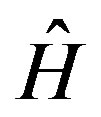 having the same set of eigenfunctions, that is ,the state is invariant to time reversal(motion reversal).
having the same set of eigenfunctions, that is ,the state is invariant to time reversal(motion reversal).
It is proved that time reversal operator is antiunitary [4], i.e.
 (4)
(4)
It is also anti-linear operator.
Kramer theorem [4,6]: It can be proved that 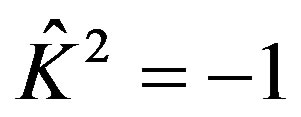 corresponding to J value of half odd integer, i.e. fermions, there will be the new double degeneracy by time reversal; and
corresponding to J value of half odd integer, i.e. fermions, there will be the new double degeneracy by time reversal; and  corresponding to J value of integer, i.e. bosons, with no double degeneracy.
corresponding to J value of integer, i.e. bosons, with no double degeneracy.
For the time-independent Dirac equation
 (5)
(5)
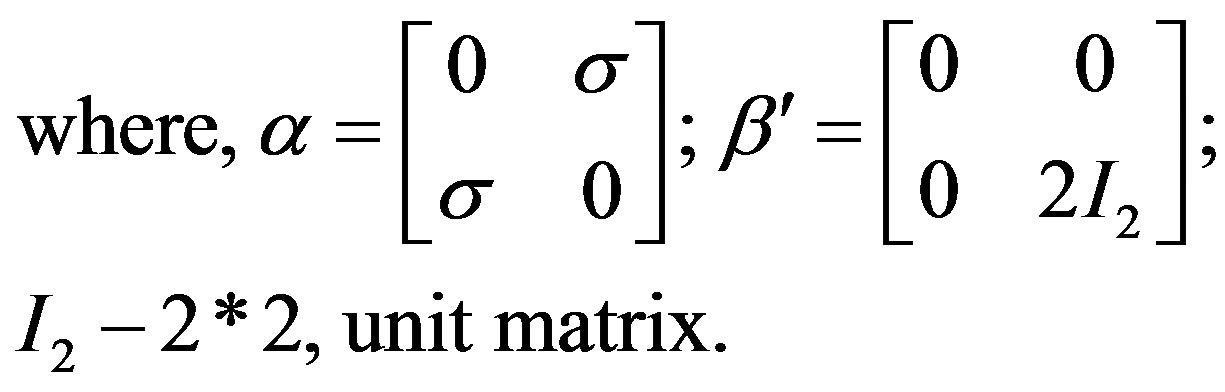 (6)
(6)
And Pauli spins matrices
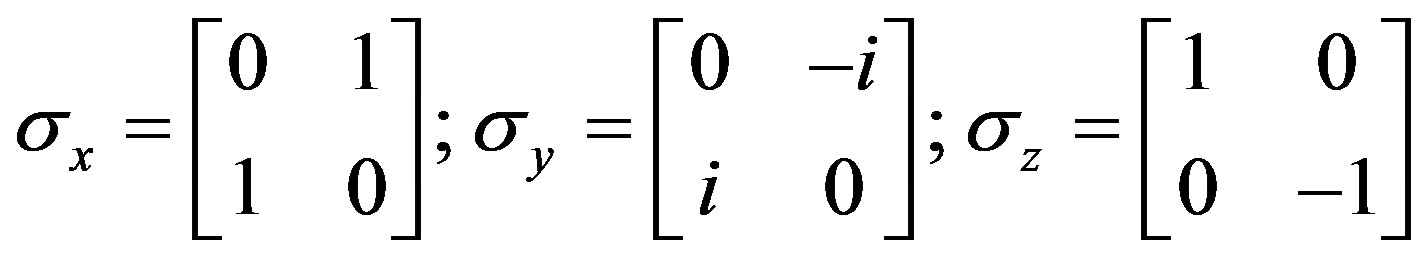 (7)
(7)
If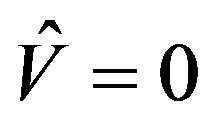 , It is the Dirac equation of free electrons.
, It is the Dirac equation of free electrons.
Now,time reversal operator is defined using another equivalent method, i.e. Kramer theorem [4,7], in which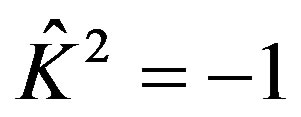 , that is
, that is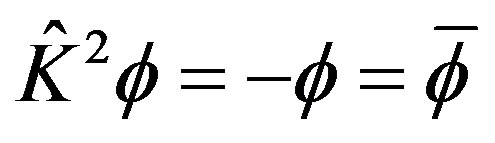 , in which the state are recovered by twice of time reversal, however, the wave function is changed to the negative; If
, in which the state are recovered by twice of time reversal, however, the wave function is changed to the negative; If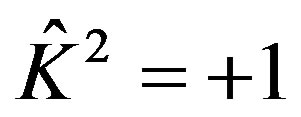 , that is
, that is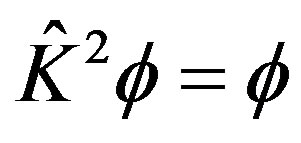 , in which the state are recovered by twice of time reversal, the wave function is unchanged. Then
, in which the state are recovered by twice of time reversal, the wave function is unchanged. Then  and
and 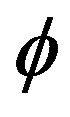 are said to form a Kramers pair .Therefore, the operator can be expanded in terms of Kramer’s partners
are said to form a Kramers pair .Therefore, the operator can be expanded in terms of Kramer’s partners 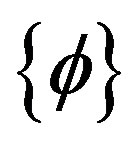 and
and . For example, Hermitian of one-electron operator [5,7] is defined as follows
. For example, Hermitian of one-electron operator [5,7] is defined as follows
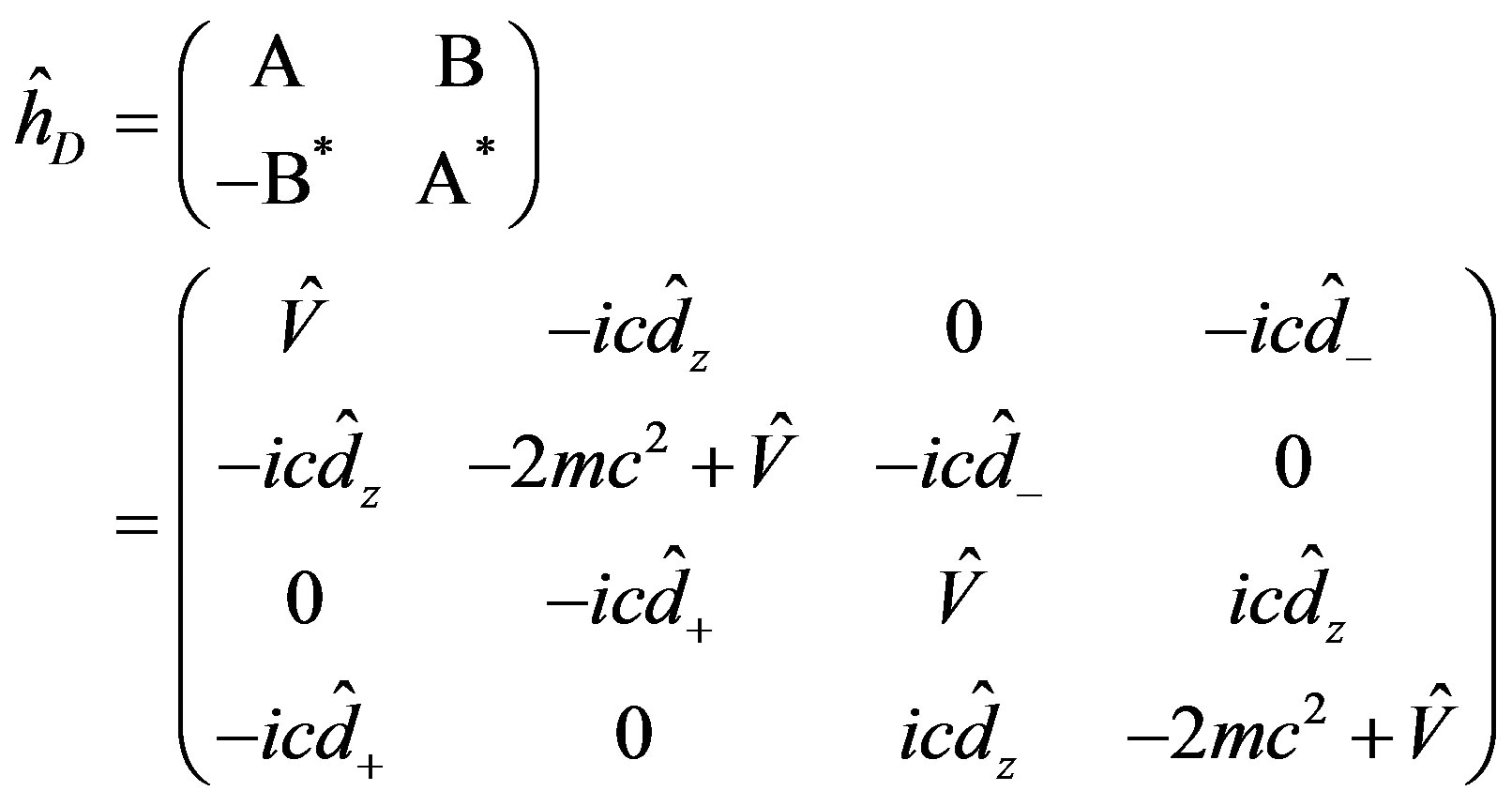 (8)
(8)
where
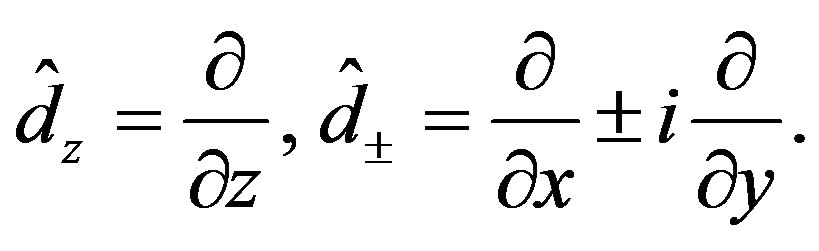 (9)
(9)
It is easy to know
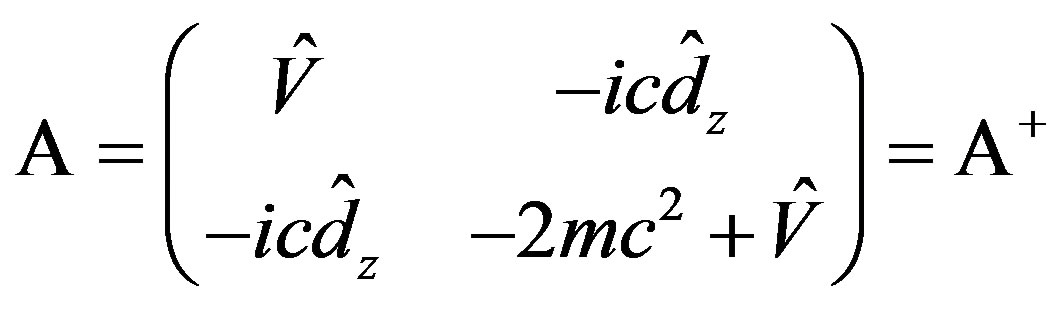 (10)
(10)
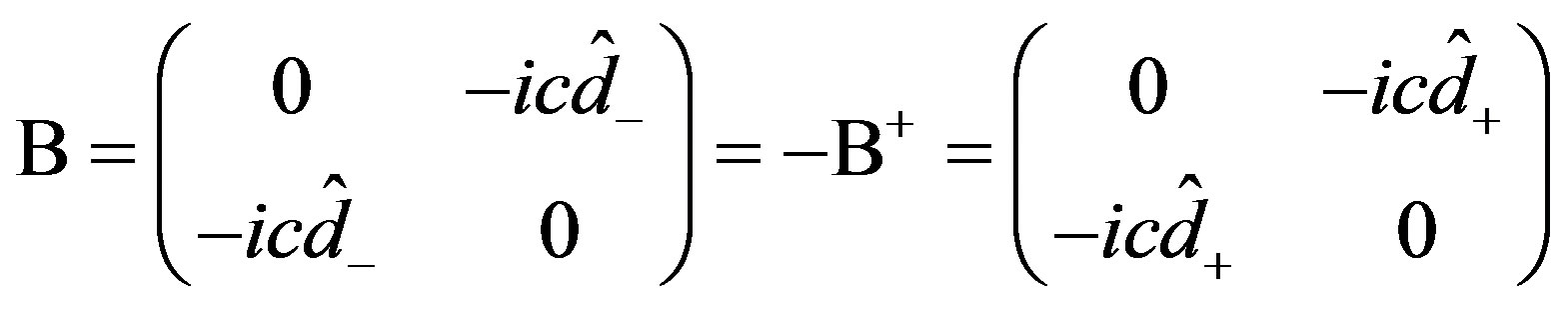 (11)
(11)
That is, A is a Hermitian and B is antihermitian. For Kramer’s partners, Dirac operator 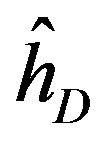 can be expressed as
can be expressed as
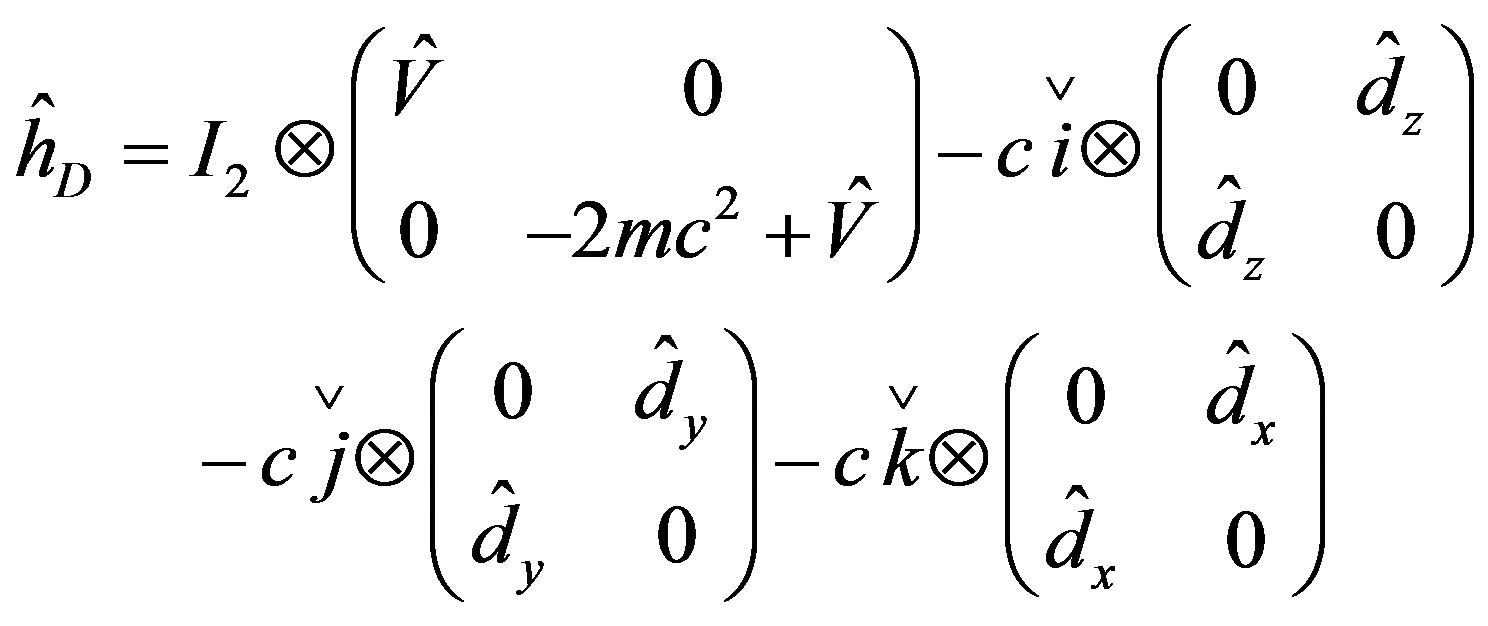 (12)
(12)
where, 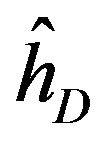 is expressed as the quaternion, which exhibits the time reversal symmetry.
is expressed as the quaternion, which exhibits the time reversal symmetry.
Quaternion algebra [8] was developed by Hamilton and Fresenius, however, limited applications of quarternion in quantum mechanics have been made in recent years.
Quaternion is expressed as
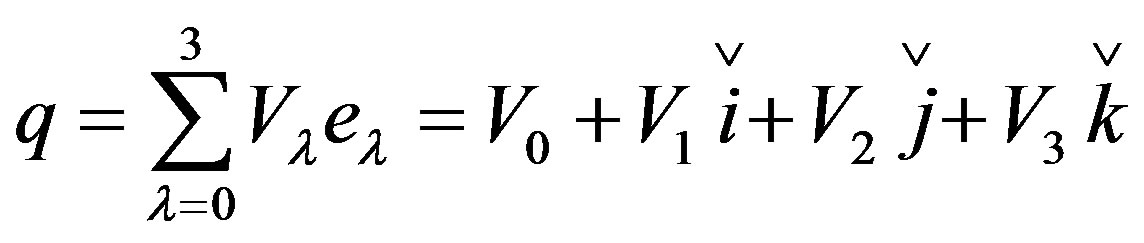 (13)
(13)
where
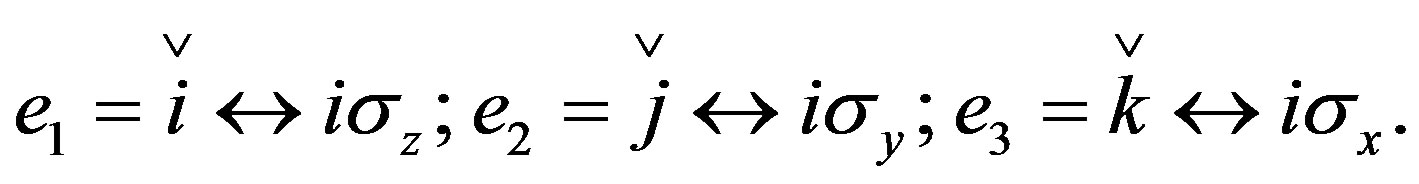 (14)
(14)
where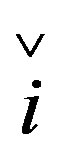 ,
, 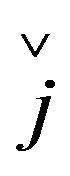 ,
,  are quaternion units, i-imaginary,
are quaternion units, i-imaginary,  ,
,  ,
, 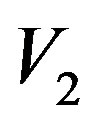 and
and 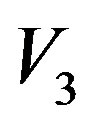 are real part,
are real part, 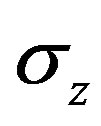 ,
, 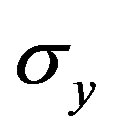 and
and 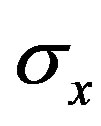 are Pauli spins matrices in (7). Quaternion includes 3-dimension complex space and one dimension real space. It is known from (7) to (11) that quaternion algebra includes both time and space reversal symmetry, then, it is called the full symmetry group, its matrix representation is called co-representation. The
are Pauli spins matrices in (7). Quaternion includes 3-dimension complex space and one dimension real space. It is known from (7) to (11) that quaternion algebra includes both time and space reversal symmetry, then, it is called the full symmetry group, its matrix representation is called co-representation. The 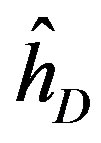 in (12) is the Dirac operator of full symmetry group. The Dirac equation can therefore be rewritten into quaternion algebra form
in (12) is the Dirac operator of full symmetry group. The Dirac equation can therefore be rewritten into quaternion algebra form
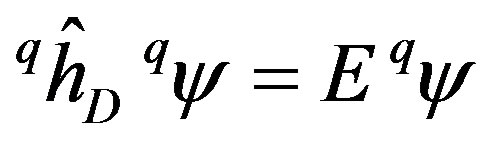 (15)
(15)
In this paper, the study of furan (C4H4O) and CHe2++ molecule are based on the full relativistic quantum mechanical theory for two-photon excitation, and the SACCI (The Symmetry Adapted Cluster/Configuration Interaction Method (SAC-CI) ) method [11] for single-photon excitation ,which would be preferable by comparison.
3. TWO PHOTON PROCESSES
The transition probability of the two photon and three photon processes are obtained from the second-order and three-order approximation coefficients of time-dependent perturbation theory [9], separately. Let us now write the Hamiltonian operator as
 (16)
(16)
where 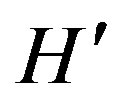 is the perturbation added on
is the perturbation added on . Following the electromagnetic theory, the x component of the perturbation
. Following the electromagnetic theory, the x component of the perturbation 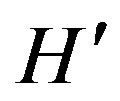 is expressed as
is expressed as
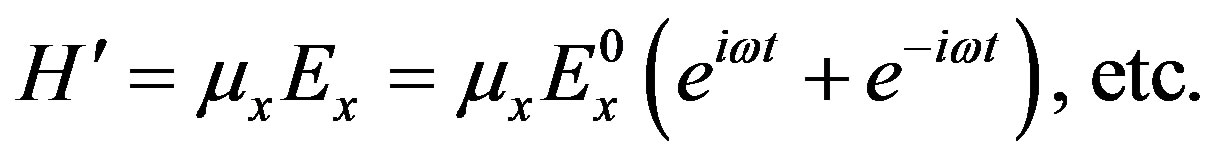 (17)
(17)
Substituting Eq.16 into the time-dependent Schrodinger equation, then
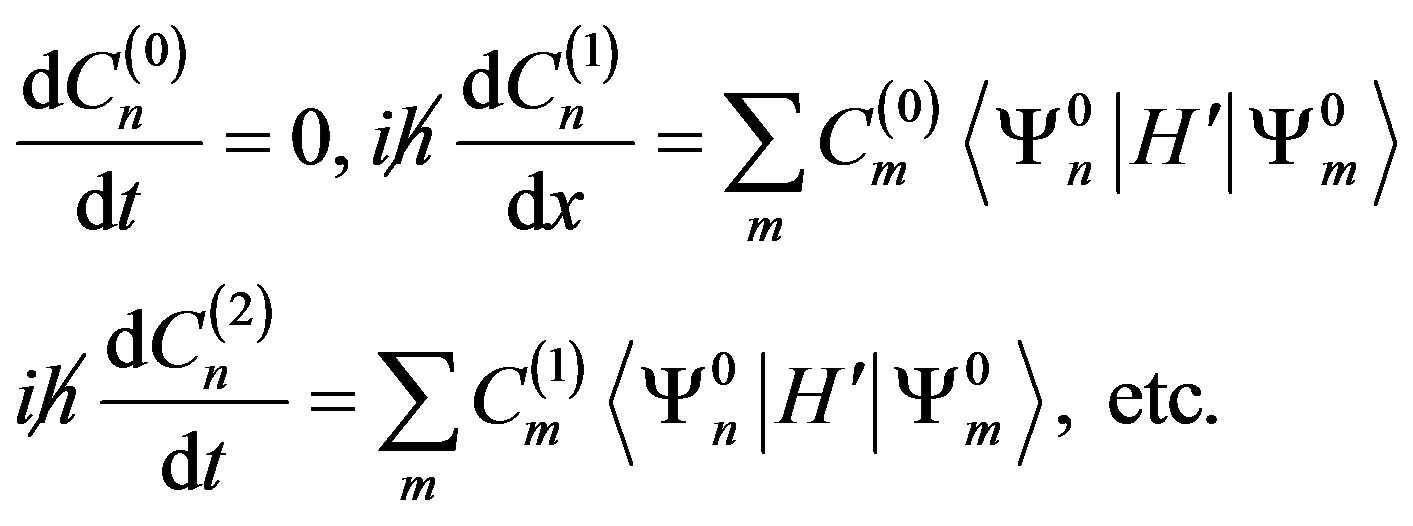 (18)
(18)
Carrying out the integration, we have the transition probabilities for the single photon and two photon processes
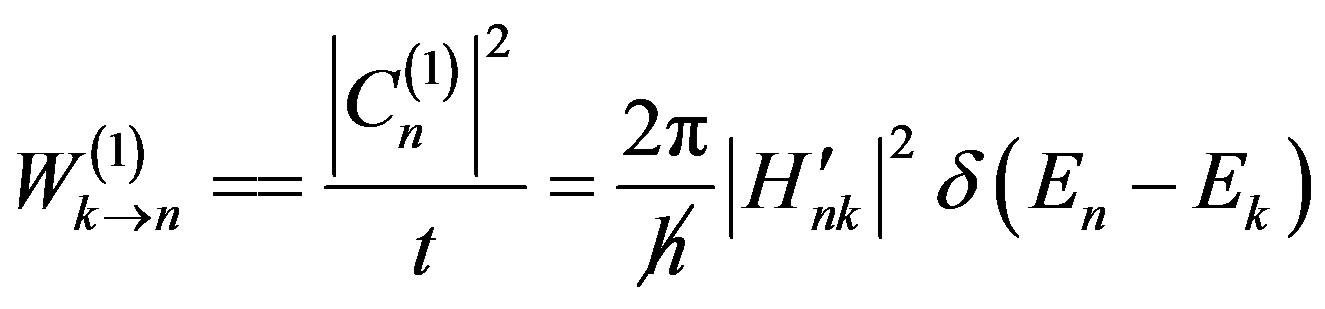 (19)
(19)
And
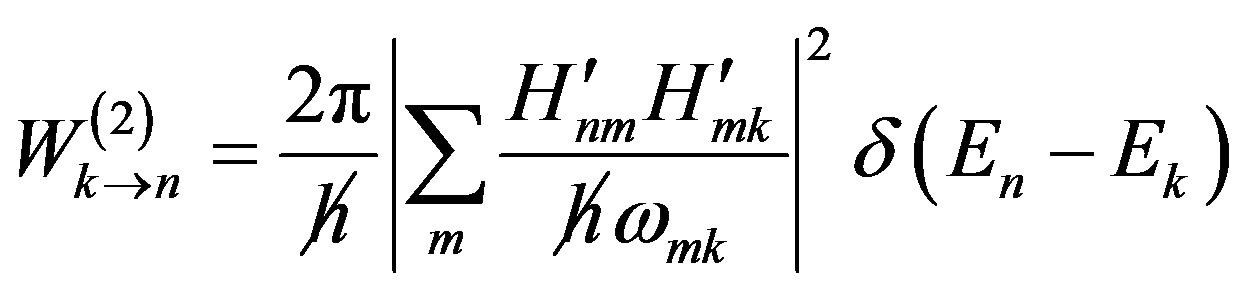 (20)
(20)
where 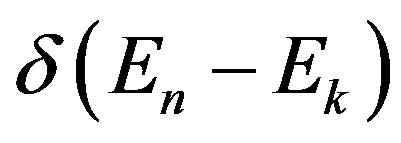 satisfies the resonance relation.
satisfies the resonance relation.
In Eq.18, the zeroth-oder coefficient, i.e. the zerothoder approximation representation is a constant, and the first and secondary approximations are also given. The transition probabilities are given in Eq.19 for singlephoton and in Eq.20 for two-photon absorptions. The use of two identical photon absorption is just a particular case of Eq.20.
The nth-order time-dependent perturbation theory is not only a mathematical method, but also with more physical significance. In fact, Göppert-Mayer noticed that the second-order perturbation theory is able to describe two-photon absorption. In the two-photon absorption, the two photons simultaneously transfer their energy to the atom. Furthermore, it became clear after Göppert-Mayer’s work that higher-order perturbation theory reveals multiphoton absorption processes.
The parity selection rules can be described as follows [10]. The Racah’s normalized electronic multipole moment is expressed as
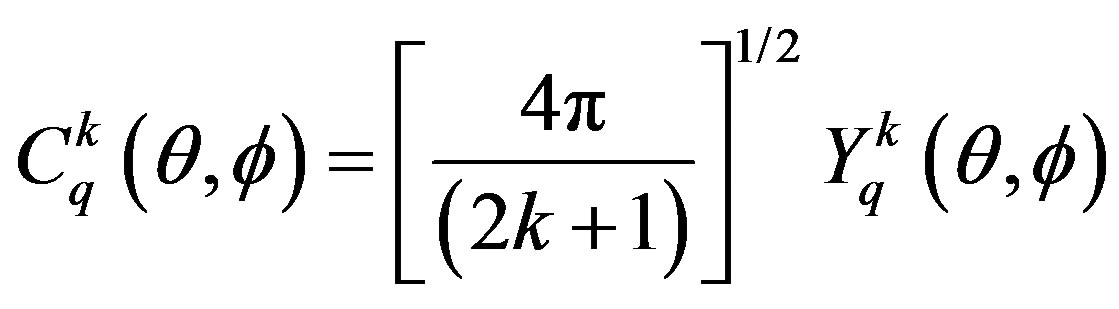 (21)
(21)
where, for k = 0, 1, 2, 3, ···, are called monopole, dipole, quadruple, octapole moments… The electronic dipole transitions of single photon processes connect two states with different parity, for operator  has an odd parity. However, for electronic dipole transitions of two photon processes, the connected states are with common parity due to the second-order approximation coefficients of Eq.18.
has an odd parity. However, for electronic dipole transitions of two photon processes, the connected states are with common parity due to the second-order approximation coefficients of Eq.18.
Symmetry selection rules based on the irreducible representation of group are the same for both single-photon and two-photon absorptions.
The transition probability is a key to apprehend the two photon processes [9]. The transition probability of single photon processes is proportional to the square of transition moment from Eq.19, i.e. to the square of electric vector which is proportional to irradiance, however, the transition probability of two photon processes is proportional to the product of two transition moment, therefore, proportional to its quadratic dependence on the irradiance. This is why the transition probability of two photon processes could be negligible at low irradiance; however, it will be increased rapidly with the irradiance.
4. TWO PHOTON EXCITATION OF C4H4O AND CHe2++
In order to review two photon excitation of furan and CHe2++, the energy, excitation energy and oscillator strength at light speed 137.036 au are listed in Table 1 and Table 2, which is compared with the results of single-photon excitation by SAC-CI method (The Symmetry Adapted Cluster/Configuration Interaction Method (SAC-CI)) [11].
For a given initial irreducible representation, the final irreducible representation is determined from the Table 3. For example, from the initial state A1 and its y components of transition moment, then, and the final state is B2.
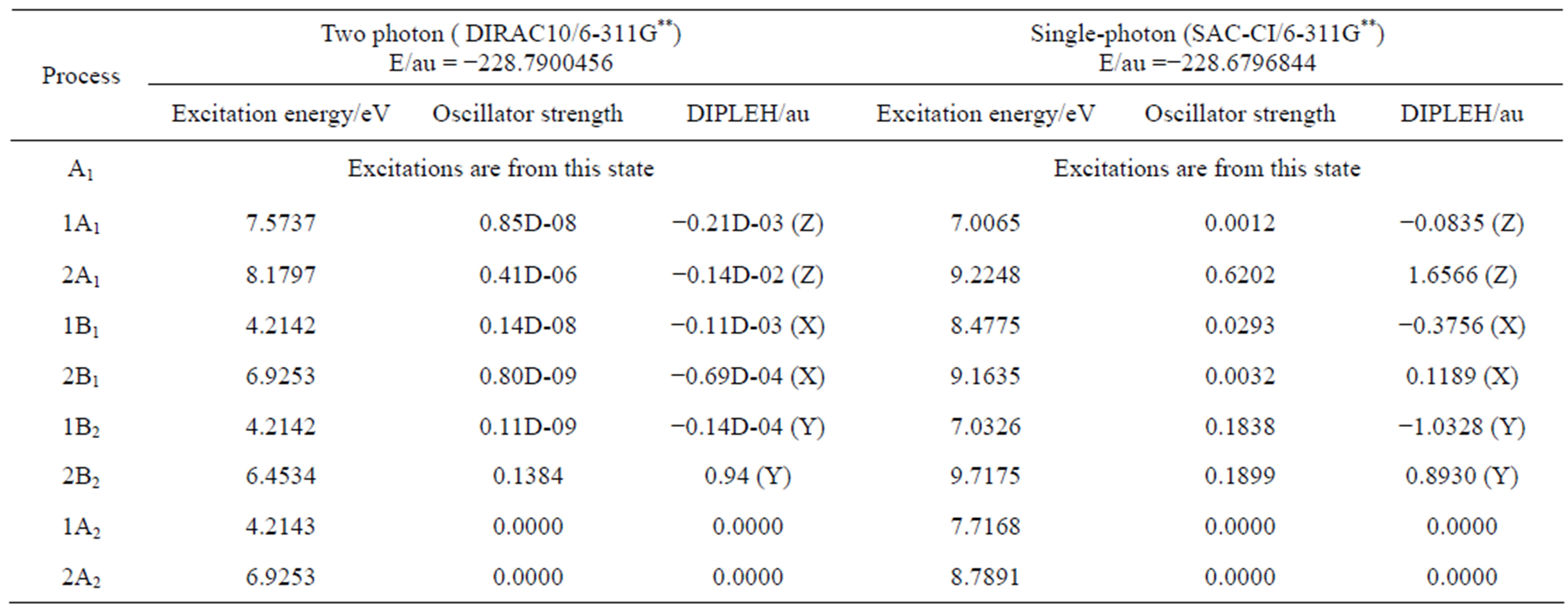
Table 1. The calculations of two photon excitation at light speed 137.036 au for furan (C4H4O), (Two photon and Single-photon both at the same geometry/Å, deg: CO = 1.3553; CH1 = 1.07693; CH = 1.07832; CC1 = 1.35563; CC = 1.4295; HCO = 115.81476; COC = 106.90016; CCO = 110.53531; HCC = 126.50286: Ground state ; DIPLEN: the component of dipole length integrals).
; DIPLEN: the component of dipole length integrals).
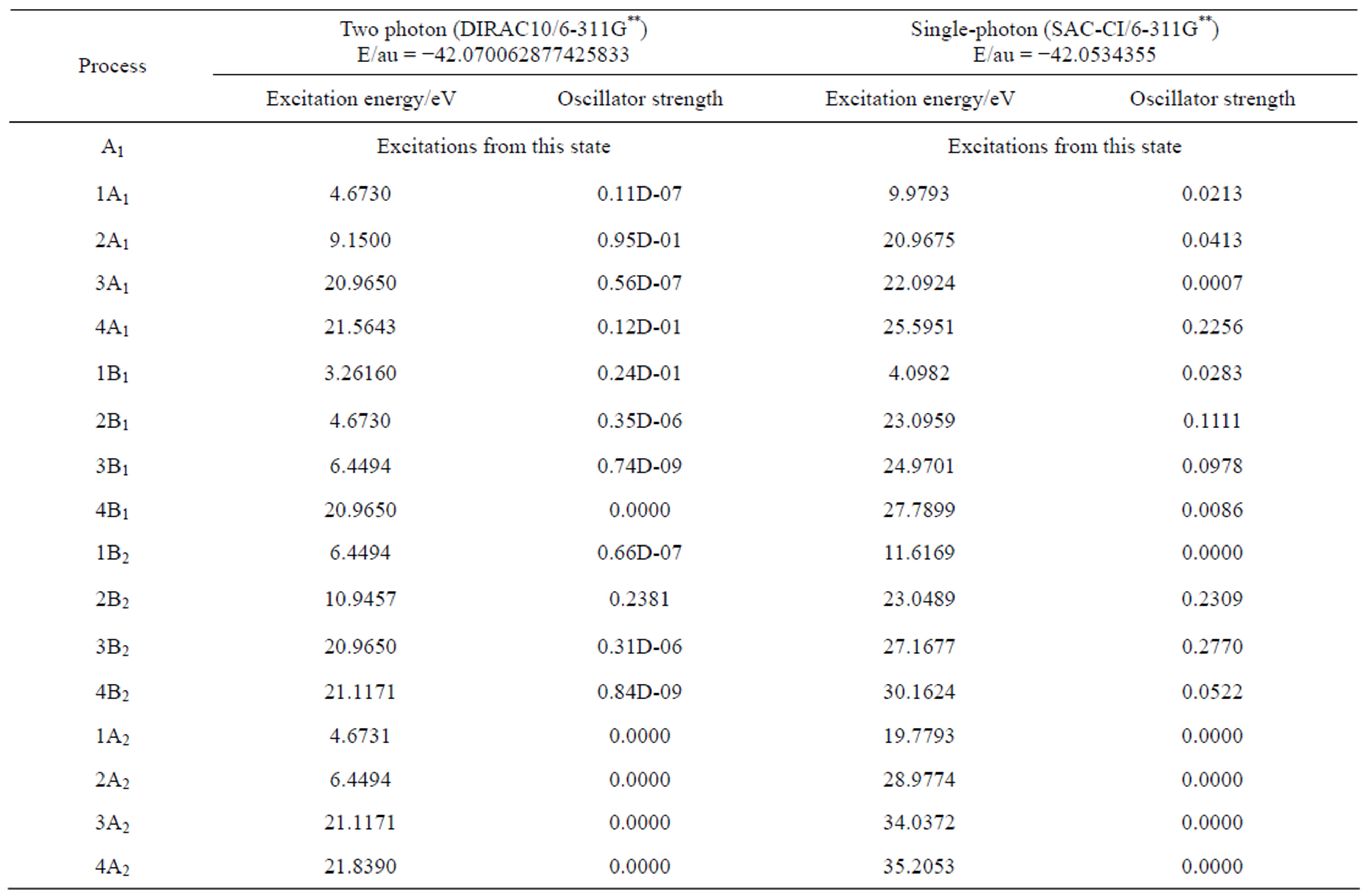
Table 2. The calculations of two photon excitation at light speed 137.036 au for CHe2++ (Two photon and Single-photon both at the same geometry/Å, deg: CHe = 1.1135; HeCHe = 102.0; Ground state ).
).
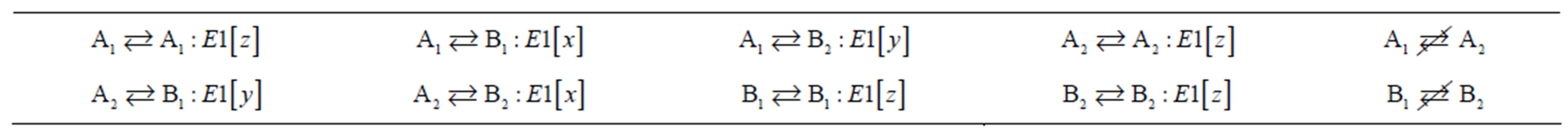
Table 3. The dipole transition moment E1 and components of transition moment for C2V.
5. CHARACTERISTIC SYMMETRY OF TWO PHOTON EXCITATION FOR C2V
In the general, people used to consider the transition probability negligible for two photon processes. From Tables 1 and 2, it is obvious that the oscillator strength of two-photon excitation is about 10−6 to 10−9 less than that of single-photon excitation. There is no much deviation in the oscillator strength of process A1 to 2B2 for both two-photon and single-photon. Therefore, we would come to the conclusion that not all the transition probability of two photon processes is negligible, it depends on the symmetry of group.
The (19) multiplied by delta function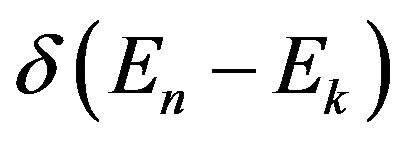 , then, it is the transition probability of single-photon absorption process with dipole integral element
, then, it is the transition probability of single-photon absorption process with dipole integral element 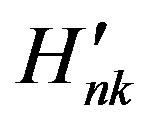 for k state to n state, which is determined by the resonance relation of single-photon process.
for k state to n state, which is determined by the resonance relation of single-photon process.
The (20) multiplied by delta function , then, it is the transition probability of two-photon absorption process with the product of dipole integral elements
, then, it is the transition probability of two-photon absorption process with the product of dipole integral elements  and
and 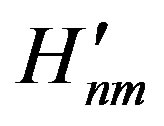 for k state to m state and m state to n state. The k state to n state is determined by the resonance relation of two-photon process, i.e.
for k state to m state and m state to n state. The k state to n state is determined by the resonance relation of two-photon process, i.e. 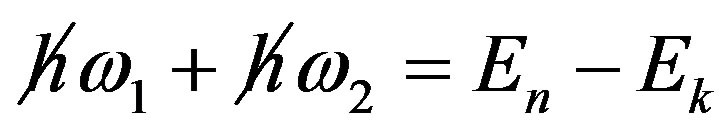 or
or  for two identical photons.
for two identical photons.
However, consider the characteristic symmetry of group C2V, both C4H4O and CHe2++ molecule are on the yz plane with the operation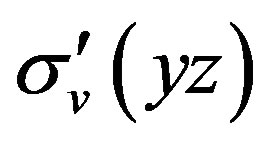 , not so as the operation
, not so as the operation 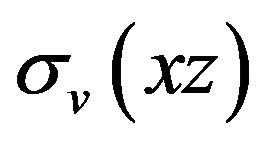 perpendicular to molecular plane, therefore, the contribution of y components of transition moment are rather significant. Therefore, the summation for all possible intermediate states m would lead to remarkable transition probability.
perpendicular to molecular plane, therefore, the contribution of y components of transition moment are rather significant. Therefore, the summation for all possible intermediate states m would lead to remarkable transition probability.
In this case, the will no much deviation for two photon and single-photon processes in the oscillator strength, such as, process A1 to 2B2. For the higher or lower excited states, at least one of intermediate transition moment elements will be quite small and its oscillator strengths negligible. The necessary and sufficient conditions are determined by the operation 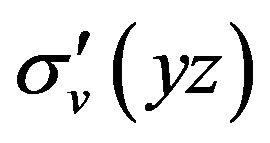 for group C2V.
for group C2V.
6. CONCLUSION
The relativistic quantum mechanical theory based on the full symmetry group or quaternion symmetry, i.e. inclusion both of space and time operations, is most suitable method for the calculation of two photon processes. Neither non-relativistic, such as DFT implemented [2] at the Gaussian 03 package, nor relativistic without time reversal would be suggested for the two photon processes.
It is found that not all the transition probability of two photon processes is negligible at low irradiance, which depends on the symmetry of group. The irreducible representation 2B2 of C2v is unexpected .There is no much deviation in the oscillator strength of process A1 to 2B2. This new phenomenon is only possible to be explored by the symmetrical consideration: the necessary and sufficient condition is molecular plane coincident with yz plane or the operation  for group C2V.
for group C2V.
If two photon process of A1 to 2B2 of furan is successfully used, it will produce much higher-contrast images for two-photon fluorescence microscopy.
REFERENCES
- Underwood, J. and Witig, C. (2004) Two-photon photodissociation of H2O via the
 state. Chemical Physics Letters, 386, 190-195. doi:10.1016/j.cplett.2004.01.030
state. Chemical Physics Letters, 386, 190-195. doi:10.1016/j.cplett.2004.01.030 - Gonc, M., Vivas, A., Luiz Silva, D., de Boni, L., Zalesny, R., Bartkowiak, W. and Mendon, C.R. (2011) Two-photon absorption spectra of carotenoids compounds. Journal of Applied Physics, 109, 103529-103537 doi:10.1063/1.3590157
- Zhu, Z.H. and Tang, Y.J. (2011) Spectral fine structure of the atomic ground states based on full relativistic theory. Chinese Optics Letters, 9, 010204-010208. doi:10.3788/COL201109.010204
- Zhu, Z.H. (1997; 2007) Atomic and molecular reaction statics. Science Press, Beijing.
- Saue, T. and Jensen, H.J.Aa (1999) Quaternion symmetry in relativistic molecular calculations. Journal of Chemical Physics, 111, 6211-6222. doi:10.1063/1.479958
- Zhu, Z.H. (2007) The atomic and molecular reaction statics. Science in China Series G: Physics Mechanics and Astronomy, 50, 581-590.
- Saue, T. and Jensen, H.J.Aa. (2003) Linear response at the 4-component relativistic level. Journal of Chemical Physics, 118, 522-536.
- Charlie, H. (1976) Introduction to mathematical physics. Prentice Hall, Inc., Engleewood Cliffs.
- Lin, S.H., Fujimura, Y., Neusser, H.J. and Sching, E.W. (1984) Multiphoton spectroscopy of molecules. Academic Press, Inc., New York, 7-69.
- Silver B.L. (1976) Irreducible tensor method. Academic Press, New York, 71.
- Nakatsuji, H. and Ehara, M. (1993) Symmetry-adapted cluster-configuration interaction method applied to highspin multiplicity. Journal of Chemical Physics, 98, 7179- 7184. doi:10.1063/1.464709

