Natural Science
Vol.4 No.1(2012), Article ID:17028,3 pages DOI:10.4236/ns.2012.41005
Water-shedding ability of waterfowl and the brachistochrone problem
![]()
Department of Chemical and Natural Gas Engineering, Texas A & M University-Kingsville, Kingsville, USA; kfdls00@tamuk.edu, dschrube@ksu.edu
Received 22 November 2011; revised 27 December 2011; accepted 7 January 2012
Keywords: Brachistochrone; Duck; Breast
ABSTRACT
The hypothesis is taken that the shape of a duck breast is as to shed water drops in minimum time. If a water drop is further assumed to be a frictionless bead, then analogy arises with the classic brachistochrone problem. Here a frictionless bead is one constrained to fall along a wire threading it so that it travels between two arbitrary points without friction. The brachistochrone problem is to specify the shape of that wire so that the bead completes its fall in minimum time. The shape of that wire is called a cycloid curve and it is the solution to the brachistochrone problem. Waterfowl might desire that water drops shed their breast region in minimum time and those drops resemble beads in the brachistochrone problem. Thus it might be expected that waterfowl breast profiles resemble the brachistochrone curve (cycloid), and strikingly they do. We find further this match is statistically significant compared to the general bird population, in support of the hypothesis.
1. INTRODUCTION
From Figure 1 it is immediately and strikingly apparent waterfowl breasts resemble the cycloid, the solution to the brachistochrone problem (the cycloid is sometimes called the brachistochrone).
The profile that waterfowl present in the wild may be related to their ability to shed water. It seems reasonable that if you were a duck and you found water, even drops of water, about the head and breast area in a non-submerged position, you would want to repel or shed that water in the best possible way. “Best” might be defined as “fastest.” If drops appear by some circumstance in the region of a duck’s head and breast, it might be desirable to slide it off the those areas in the fastest way, to a low point, minimum point, in the shortest time.
This problem is analogous to the classic brachistochrone problem. Here a frictionless bead on a wire has gravity operating on it to make the bead fall along the wire. The path the bead will take depends on the shape of the wire. The problem is to specify the shape of the path (which the bead will take) so that it reaches the bottom the fastest. If the bead falls the fastest (completes it’s flight path in minimum time) the path has the shape of the figure known as a cycloid (once again, sometimes called the brachistochrone). In other words, the brachistochrone problem is to specify the shape of the minimum time curve and the solution or answer to the brachistochrone problem is the cycloid curve (brachistochrone). This is the curve a piece of chalk would trace out on a wall if the chalk were attached to the rim of a wheel and the wheel were rolled near the wall. The first part of this paper develops the brachistochrone problem, noting particular relevance to water-shedding waterfowl. The second part compares the brachistochrone to the profile curve (geometric aspects) of waterfowl and shows the fit there is better (statistically significant) than with the general bird population. It may be that waterfowl have evolved to shed water droplets in minimum time. Evolution may have worked to solve the brachistochrone problem (We certainly do not intend here to make an evolutionary biology hypothesis, rather to merely communicate the waterfowl breast-brachistochrone congruence.)

Figure 1. Waterfowl breasts and the brachistochrone (blue line tangent to breast) show striking similarity.
2. WATER SHEDDING MECHANICS, AND THE BRACHISTOCHRONE
Again, in the brachistochrone problem, a frictionless bead on a wire slides down it by gravity [1]. Only gravity is acting, not friction, and we consider the problem with an arbitrary path. We seek the path that will connect two points displaced horizontally and vertically in gravity, in minimum time. Ordinarily that path might be a straight line. However, it works out that it is better to get the bead moving fast early, with a steep drop initially. This more than makes up for the longer path the bead must travel because of how that steep drop stretches the path. The problem is a classic and the name Bernoulli is associated with it. The word “brachistochrone” comes from the Greek for “shortest time”. The reader may be familiar with the English words chronometer and chronology, relating to time.
The “steep drop initially” referred to recalls our image of a duck breast. Random water drops thrown at the duck profile will often have a steeper initial segment of path as they fall in gravity than later portions of that fall path. This leads to the tautochrone (meaning “the same time”) property. Random water beads may form at any point along a brachistochrone like water shedding path. This is true regardless if path origins are on the bill, head (but not the flat top area), and upper neck regions, or if they fall on the breast and the lower neck regions. All drops on a given brachistochrone path will reach the bottom at this same time. Again, this is the tautochrone property. This is a property of the cycloid curve, the solution to the brachistochrone problem.
Brachistochrone analogy requires that the water drop be frictionless. The feathers are certainly oily. Feathers in their own right and because of the oil have low friction for water sliding across them. This is a qualification necessary to this analysis and water on waterfowl meet it. Further, the assumption has been taken as reasonable that the low friction of a water drop on waterfowl is approximated as being frictionless. Though the droplet mass, m, is not a point or even symmetric, it is still taken to be such that the classic brachistochrone analysis applies, briefly sketched as follows.
In the brachistochrone, the work done on the bead as it falls (by gravity, g) through distance y, mgy, must equal the gained kinetic energy of the bead at y, 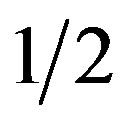 mv2:
mv2:
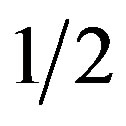 mv2 = mgy (1)
mv2 = mgy (1)
The velocity along the path, s, is v =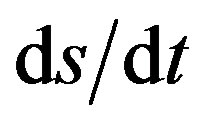 , where the differential in path length ds, is related to dx and dy as in the numerator of Eq.2. Thus
, where the differential in path length ds, is related to dx and dy as in the numerator of Eq.2. Thus 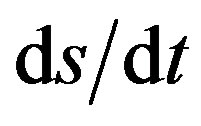 = (2gy)1/2 can be rearranged as
= (2gy)1/2 can be rearranged as
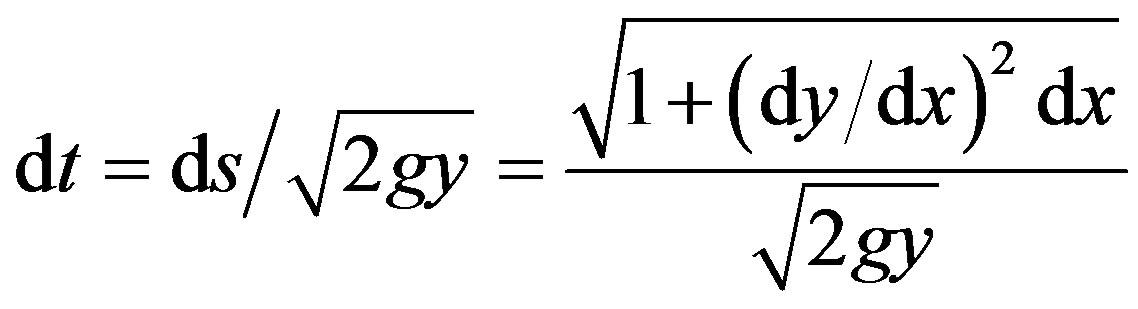 (2)
(2)
The time to fall (t is the total time of travel) is simply the integral of Eq.2 from 0 to t. The problem (again, the brachistochrone problem) is to find the function y = f(x) that will minimize bead travel time, t. To be sure, y = f(x) is a path, that is it gives the shape of the path that will connect the two given points in minimum time. Solution details are not given, but that function traces out the geometric figure know as the brachistochrone. The solution can be obtained by several methods, but one of the first methods came by the so-called calculus of variations. The cycloid (brachistochrone) is the most important special case of the class of trochoid figures, the figure traced on a wall by a point on a disk as the disk rolls along a straight line next to the wall. The brachistochrone occurs when the tracing point is on the disk perimeter. It remains to examine whether the duck breast profile resemblance to the brachistochrone is statistically distinct from the resemblance of the general bird breast to the brachistochrone. We will find that it is. The analysis could have been done at other places such as the duck bill but the breast was selected to give a specific example.
3. DUCK PROFILE COMPARISON
For our source of duck profiles we turn to a wellknown text. The Peterson Field Guide to the Birds [2] is considered by some to be the best and most authoritative such guide and good duck profiles reside in the respective section. In the frontise piece are “Roadside Silhouettes”. These are the only general collection of birds in the sitting position in this book. (Other sources [3] have waterfowl profiles but [2] has good representation of both populations). There are 28 such profiles here. As we consider these the need for a quantitative parameter indicating congruence of the brachistochrone solution curve to bird breasts is needed.
At first sight it appears obvious that ducks have a more brachistochrone like shape than the generic bird population. To get beyond appearances, however, a more quantitative indicator was sought. In that regard a deviation length and a congruence length will be defined and discussed. A deviation length from the brachistochrone curve can be identified for each attempted fit of that curve to a bird breast. The deviation length is defined here as the length of a line perpendicular from the brachistochrone curve to the bird’s breast. The congruence length is defined as a length along the brachistochrone. The steps to use these to find goodness of fit follow.
The first step in the determination of goodness of fit was to select profiles. Profiles that showed a good side view from the duck group and the general frontise group were numbered. By dividing by the respective maximums from these two groups, the profile identifications filled a unit interval for each group. A Brownian sampling was done from the unit intervals using a standard pair of dice. Possible outcomes for a throw of the dice have a maximum and a minimum. Division of a random throw number by the maximum minus minimum number gave a position on the unit interval. The profile nearest that position was selected. In this way five random profiles were selected from the duck group and the general bird group. Next those profiles were dilated to have a same length over all. Thus differences in bird size and illustration size were nullified. A brachistochrone that had a good fit to the duck group was selected (the duck group was highly uniform so the brachistochrone fit was not greatly dependent on which duck was selected). Each profile was fitted with the brachistochrone. When the deviation length over the congruence was ten percent, the congruence length was noted. The congruence length treated after this manner became the goodness of fit parameter for this study. (There are many mathematical methods of curve fitting that could have been used.) Next we will look at how the fit parameter was treated.
The comparison of means for the duck group with the general group at the 95-confidence level was used in a standard statistical treatment of the fit parameter. The average for the congruence lengths (5 for the ducks) can be compared to the average of the lengths (5 again in this group) of the general bird population. Comparison of means via the “t” test finally requires the standard deviation for the two groups besides the t values of course [4]. The congruence with the brachistochrone for the ducks compared to the general bird population is significant at better than the 95% confidence level.
We have been talking about the duck group versus the general bird group. To be sure we mean the duck group brachistochrone fit with the breast profile and the same for the general bird group. The fit is significantly better with the duck group (and we might believe that true for waterfowl in general). The brachistochrone is associated with faster water shedding. The significance to the bird groups is that waterfowl (or any animal group with similar brachistochrone shaped anatomy and qualifications) will have water-shedding ability for that anatomy according to this analysis. Note for example the bill area of waterfowl. By inspection it should fit the brachistochrone well, and hence shed water well. We have considered the duck to have water drops along the breast area. This could occur from sudden emergence and water formation into beads or rain falling on the area forming beads. We have not considered waterfowl in other positions such as when they take off, for example. There, other factors such as those similar to stagnation pressures act on the water bead [5]. Such issues, while important, are outside the point we wish to make.
4. ACKNOWLEDGEMENTS
Steve Smith (then at Texas A & M U-K) and Jack Cully (Kansas State U) contributions are gratefully acknowledged.
REFERENCES
- Thomas, G.B. Jr. (1960) Calculus and analytic geometry. 3rd Edition, Addison-Wesley, Reading, 565-571.
- Peterson, R.T. (1980) A field guide to the birds. 4th Edition, Houghton Mifflin Co., Boston.
- Kortright, F.J. (1967) The ducks, geese and swans of North America. The Stackpole Company, Harrisburg, Wildlilfe Management Institute, Washington, DC.
- Box, G.E.P., Hunter, W.G. and Hunter, J.S. (1978) Statistics for experimenters. John Wiley & Sons Ltd., Chichester, 203-207.
- Bejan, A. (2004) Convection heat transfer. 3rd Edition, Wiley, New York, 63-66.

