
Received 21 August 2014; revised 18 September 2014; accepted 6 October 2014
ABSTRACT
Two-phase fluid properties such as entropy, internal energy, and heat capacity are given by thermodynamically defined fit functions. Each fit function is expressed as a temperature function in terms of a power series expansion about the critical point. The leading term with the critical exponent dominates the temperature variation between the critical and triple points. With 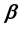 being introduced as the critical exponent for the difference between liquid and vapor densities, it is shown that the critical exponent of each fit function depends (if at all) on
being introduced as the critical exponent for the difference between liquid and vapor densities, it is shown that the critical exponent of each fit function depends (if at all) on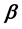 . In particular, the critical exponent of the reciprocal heat capacity
. In particular, the critical exponent of the reciprocal heat capacity 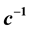 is
is 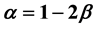 and those of the entropy
and those of the entropy  and internal energy
and internal energy 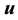 are
are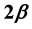 , while that of the reciprocal isothermal compressibility
, while that of the reciprocal isothermal compressibility 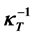 is
is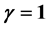 . It is thus found that in the case of the two-phase fluid the Rushbrooke equation conjectured
. It is thus found that in the case of the two-phase fluid the Rushbrooke equation conjectured  combines the scaling laws resulting from the two relations
combines the scaling laws resulting from the two relations 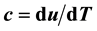 and
and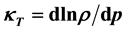 . In the context with
. In the context with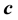 , the second temperature derivatives of the chemical potential
, the second temperature derivatives of the chemical potential 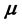 and vapor pressure
and vapor pressure  are investigated. As the critical point is approached,
are investigated. As the critical point is approached, 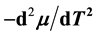 diverges as
diverges as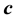 , while
, while ![]() converges to a finite limit. This is explicitly pointed out for the two- phase fluid, water (with
converges to a finite limit. This is explicitly pointed out for the two- phase fluid, water (with![]() ). The positive and almost vanishing internal energy of the one-phase fluid at temperatures above and close to the critical point causes conditions for large long-wavelength density fluctuations, which are observed as critical opalescence. For negative values of the internal energy, i.e. the two-phase fluid below the critical point, there are only microscopic density fluctuations. Similar critical phenomena occur when cooling a dilute gas to its Bose-Einstein condensate.
). The positive and almost vanishing internal energy of the one-phase fluid at temperatures above and close to the critical point causes conditions for large long-wavelength density fluctuations, which are observed as critical opalescence. For negative values of the internal energy, i.e. the two-phase fluid below the critical point, there are only microscopic density fluctuations. Similar critical phenomena occur when cooling a dilute gas to its Bose-Einstein condensate.
Keywords:
Critical Condition U = 0, Critical Opalescence, Rushbrooke Equation, Thermodynamic Fit Functions for Saturated Water, Vapor and Liquid Volumes, Vapor Pressure, Chemical Potential, Entropy, Internal Energy, Free Energy, Heat Capacity
![]()
1. Introduction
An essential property of matter is its structure, i.e. the distribution of its constituents in space and time as governed by inter-particle forces [1] . We are concerned here with the electrically and magnetically neutral single-component gas under steady-state conditions, which are thermodynamically defined in the immediate vicinity of the critical point and below it.
Andrews’s discovery of critical opalescence in carbon dioxide in 1869 stimulated numerous investigations of critical phenomena. The experimental observations on fluids show that a colorless gas in a narrow temperature range ![]() above its critical temperature
above its critical temperature ![]() suddenly becomes opaque and changes color and, at
suddenly becomes opaque and changes color and, at![]() , exists as a two-phase fluid of different densities in volumes that are sharply separated by an interface surface a few molecular layers thick. The endeavor to explain theoretically the observations constituted a huge challenge. The course of a century then saw the development of the familiar phenomenological theories of a van der Waals gas, of the stable and unstable thermodynamic equilibrium formulated by Gibbs, of the correlation of fluctuations, of the scaling laws, including the hierarchical reference theory (renormalization group techniques), and of the Monte Carlo computer methods (see [2] ).
, exists as a two-phase fluid of different densities in volumes that are sharply separated by an interface surface a few molecular layers thick. The endeavor to explain theoretically the observations constituted a huge challenge. The course of a century then saw the development of the familiar phenomenological theories of a van der Waals gas, of the stable and unstable thermodynamic equilibrium formulated by Gibbs, of the correlation of fluctuations, of the scaling laws, including the hierarchical reference theory (renormalization group techniques), and of the Monte Carlo computer methods (see [2] ).
An insight into the nature of a fluid in the critical region is afforded by Figure 1, which for water of mass ![]() [g] and critical density
[g] and critical density ![]() in the volume
in the volume ![]() [cm3] shows the different fluid states as a function of the temperature
[cm3] shows the different fluid states as a function of the temperature![]() . Below
. Below![]() ,
, ![]() is distributed as condensed mass
is distributed as condensed mass ![]() with the density
with the density ![]() in the sub-volume
in the sub-volume ![]() and as vapor mass
and as vapor mass ![]() with the density
with the density ![]() in the sub-volume
in the sub-volume![]() . This gas in thermodynamic equilibrium existing in two phases is called a saturated fluid. As thermodynamic theory teaches, as the only independent variable of the saturated fluid that can be chosen is the saturation temperature
. This gas in thermodynamic equilibrium existing in two phases is called a saturated fluid. As thermodynamic theory teaches, as the only independent variable of the saturated fluid that can be chosen is the saturation temperature![]() , since the other field variables possible, viz. vapor pressure
, since the other field variables possible, viz. vapor pressure ![]() and chemical potential
and chemical potential ![]() are unique functions of
are unique functions of![]() .
.
Every thermodynamic quantity of the saturated fluid, ![]() , can thus be represented as a function of
, can thus be represented as a function of![]() . The absolute values both of the fluid,
. The absolute values both of the fluid, ![]() , and of the fluid phases, vapor,
, and of the fluid phases, vapor, ![]() , and condensate (liquid, solid),
, and condensate (liquid, solid), ![]() , are proportional to the mass in the volume considered. As extensive quantities they have additive properties, i.e. they satisfy the equations
, are proportional to the mass in the volume considered. As extensive quantities they have additive properties, i.e. they satisfy the equations
![]() (1)
(1)
The mass-specific quantities ![]() and
and ![]() contain the complete thermodynamic information on the fluid state [3] . The difference
contain the complete thermodynamic information on the fluid state [3] . The difference ![]() gives the difference of the thermodynamic properties of
gives the difference of the thermodynamic properties of ![]() in the volumes
in the volumes ![]() and
and ![]() and is called an order parameter. The quantity
and is called an order parameter. The quantity ![]() can be expressed by the quantities
can be expressed by the quantities![]() ,
, ![]() , and
, and![]() :
:
![]() (2)
(2)
The quotient ![]() is a function of the vapor pressure
is a function of the vapor pressure![]() , and the quotient
, and the quotient ![]() a function of the chemical potential
a function of the chemical potential![]() :
:
![]() (3)
(3)
and
![]() (4)
(4)
The vapor pressure is a positive, convexly curved, monotonically increasing function of the temperature and the chemical potential a negative, concavely curved, monotonically decreasing function of the temperature. Open questions on the thermodynamic properties of ![]() and
and![]() , in particular in the critical region, are dealt with in Sections 3 and 7.
, in particular in the critical region, are dealt with in Sections 3 and 7.
Equation (2) can be transformed to
![]() (5)
(5)
Equation (5) yield, for example,![]() .
.
Relations (1)-(5) represent the Gibbs equations for calculating![]() ,
, ![]() , and
, and ![]() of the saturated fluid. One might think that the job of setting up generally valid fit formulae, i.e. applicable to every two-phase fluid has already been done. But this is not so. The literature yields, e.g. for water, only formulae for industrial use ([4] - [6] ) which do not correctly give the physical picture of the two-phase fluid in the critical region.
of the saturated fluid. One might think that the job of setting up generally valid fit formulae, i.e. applicable to every two-phase fluid has already been done. But this is not so. The literature yields, e.g. for water, only formulae for industrial use ([4] - [6] ) which do not correctly give the physical picture of the two-phase fluid in the critical region.
The objective of this study is to represent the quantities![]() ,
, ![]() , and
, and ![]() in the region between the triple point and the critical point as thermodynamic fit functions dependent on the temperature (Sections 4-9). The representation of a fit function by an order parameter expanded around the critical point is based on the knowledge of the behavior of the fluid in the critical region.
in the region between the triple point and the critical point as thermodynamic fit functions dependent on the temperature (Sections 4-9). The representation of a fit function by an order parameter expanded around the critical point is based on the knowledge of the behavior of the fluid in the critical region.
2. Thermodynamics of Critical Phenomena
The thermodynamical physics of critical phenomena above and below the critical point is extensively treated in the literature (e.g. [2] [7] -[10] ). Critical phenomena occur under the natural boundary condition of the vanishing value of the internal energy, ![]() [11] . In the immediate vicinity of the critical point the one-phase fluid is in unstable equilibrium on transition to the two-phase fluid, which is then in stable equilibrium.
[11] . In the immediate vicinity of the critical point the one-phase fluid is in unstable equilibrium on transition to the two-phase fluid, which is then in stable equilibrium.
Thermodynamics describes the macroscopic state of the fluid by means of the quantities![]() ,
, ![]() ,
, ![]() , and
, and ![]() and thus cannot delve into the microscopic processes actually occurring in the particle interactions taking place in the fluid. The effect of attractive and repulsive forces among interacting particles on the internal energy
and thus cannot delve into the microscopic processes actually occurring in the particle interactions taking place in the fluid. The effect of attractive and repulsive forces among interacting particles on the internal energy ![]() is that
is that ![]() has negative sign for fluid temperatures below
has negative sign for fluid temperatures below ![]() and positive sign above.
and positive sign above. ![]() can be treated as the sum of two energy contributions, viz. the potential energy
can be treated as the sum of two energy contributions, viz. the potential energy![]() , whose gradient yields the attractive forces, and the thermal energy
, whose gradient yields the attractive forces, and the thermal energy![]() , which is assigned to the sum of kinetic, vibrational and rotational particle energies. As the result, Figure 2 shows for saturated water (under the same conditions as in Figure 1) the internal energy
, which is assigned to the sum of kinetic, vibrational and rotational particle energies. As the result, Figure 2 shows for saturated water (under the same conditions as in Figure 1) the internal energy ![]() and the estimates
and the estimates ![]() and
and ![]() in liquid and vapor as functions of the mean particle separation, represented by
in liquid and vapor as functions of the mean particle separation, represented by
the normalized density values ![]() in the regions
in the regions ![]() with
with ![]() [K] and
[K] and![]() . For an estimation
. For an estimation
it is taken for granted that the thermal particle energy increases proportionally as the saturation temperature![]() ,
,![]() . The empirical value
. The empirical value ![]() is given by
is given by ![]() [J/g]/273.16 [K] = 1.26918 [J/(g
[J/g]/273.16 [K] = 1.26918 [J/(g![]() K)]. To calculate
K)]. To calculate![]() ,
, ![]() is multiplied by the mass
is multiplied by the mass![]() . This yields in the liquid phase an initially
. This yields in the liquid phase an initially
expected increase ![]() and on reaching the maximum value 668 [J] at about
and on reaching the maximum value 668 [J] at about![]() ,
, ![]() [K],
[K], ![]() [g] a continuous decrease to the critical value
[g] a continuous decrease to the critical value ![]() [J]. With
[J]. With ![]() the decrease is continued in the vapor phase. The product
the decrease is continued in the vapor phase. The product ![]() continuously decreases as the particle separation increases; at
continuously decreases as the particle separation increases; at ![]() the value
the value ![]() [J] is assumed. As
[J] is assumed. As
![]()
Figure 2. Internal energy![]() , estimated thermal energy
, estimated thermal energy ![]() and potential energy
and potential energy ![]() of water mass
of water mass ![]() in liquid and vapor as functions of the normalized particle separation
in liquid and vapor as functions of the normalized particle separation![]() . It is assumed that
. It is assumed that![]() , where
, where![]() ;
;![]() ;
; ![]() degrees of freedom of two H-bridged water molecules;
degrees of freedom of two H-bridged water molecules;![]() ,
, ![]() ,
, ![]() ,
,![]() ; critical values:
; critical values:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
![]() (with
(with ![]() [g]) can be calculated according to Equation (5), it is possible to estimate the potential
[g]) can be calculated according to Equation (5), it is possible to estimate the potential ![]() numerically.
numerically. ![]() is always negative. The resulting repulsion and attraction forces between the particles are equal and opposite at the critical point, which is expressed in Figure 2 by the fact that the curves
is always negative. The resulting repulsion and attraction forces between the particles are equal and opposite at the critical point, which is expressed in Figure 2 by the fact that the curves![]() ,
, ![]() , and
, and ![]() all are continuous there. Qualitative information about mean-field strength of forces in liquid and vapor can be obtained from
all are continuous there. Qualitative information about mean-field strength of forces in liquid and vapor can be obtained from ![]() and
and![]() .
.
The positive and negative regions of the fluid internal energy ![]() are shown in Figure 3 for water in the pressure vs volume diagram. They are separated by the isotherm
are shown in Figure 3 for water in the pressure vs volume diagram. They are separated by the isotherm ![]() above the critical pressure
above the critical pressure ![]() (dashed line) and the vapor pressure
(dashed line) and the vapor pressure ![]() below
below ![]() and
and ![]() (solid line). Along the dashed line there is a continuous change in the density passing through positive and negative regions of
(solid line). Along the dashed line there is a continuous change in the density passing through positive and negative regions of![]() . The solid lines represent the vapor pressure at temperature
. The solid lines represent the vapor pressure at temperature ![]() and are the loci of the first-order phase transition due to the jump between low-density vapor and high-density condensate. The jump is combined with a different fluid structure in each phase.
and are the loci of the first-order phase transition due to the jump between low-density vapor and high-density condensate. The jump is combined with a different fluid structure in each phase.
A fluid state of ![]() is characterized by an ensemble of particles freely moving in a structureless homogeneous phase. In contrast, a fluid state of
is characterized by an ensemble of particles freely moving in a structureless homogeneous phase. In contrast, a fluid state of ![]() is characterized by an ensemble of particles bound in a more or less structured form as a result of particle self-organization under certain constraints, e.g. liquid, solid, and Bose-Einstein condensate (BEC) [12] , each with its specific thermodynamic property. As an example, Figure 4 shows the variations in internal energy of vapor and condensates as functions of their phase-specific volumes and the saturation temperature, respectively, for the water mass of 1 [g].
is characterized by an ensemble of particles bound in a more or less structured form as a result of particle self-organization under certain constraints, e.g. liquid, solid, and Bose-Einstein condensate (BEC) [12] , each with its specific thermodynamic property. As an example, Figure 4 shows the variations in internal energy of vapor and condensates as functions of their phase-specific volumes and the saturation temperature, respectively, for the water mass of 1 [g].
The discontinuities of![]() , represented as circles in Figure 5, indicate the phase transitions of bulks of different structures. States of different aggregation exhibit qualitatively different properties. Adding energy
, represented as circles in Figure 5, indicate the phase transitions of bulks of different structures. States of different aggregation exhibit qualitatively different properties. Adding energy ![]() to the fluid at fixed temperature distributes a surplus of the one bulk phase at the expense of the other [1] . Local variations of internal energy couplings between particles change the bulk structures. A structural change is thermodynamically described by an increase in internal energy
to the fluid at fixed temperature distributes a surplus of the one bulk phase at the expense of the other [1] . Local variations of internal energy couplings between particles change the bulk structures. A structural change is thermodynamically described by an increase in internal energy ![]() as a result of increasing system entropy
as a result of increasing system entropy![]() , i.e. by
, i.e. by![]() . Changes in the bulk structure occur close to absolute zero, at the triple point and the critical point. The circles in Figure 1 and Figure 5 give the phase transitions for the functions
. Changes in the bulk structure occur close to absolute zero, at the triple point and the critical point. The circles in Figure 1 and Figure 5 give the phase transitions for the functions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . It is seen that the phase transition near absolute zero at the critical temperature of the BEC,
. It is seen that the phase transition near absolute zero at the critical temperature of the BEC, ![]() , refers to the mass
, refers to the mass![]() , at
, at ![]() to the mass
to the mass![]() , and at
, and at ![]() to the masses
to the masses ![]() and
and![]() , where it holds that
, where it holds that![]() . The discontinuous transition in the
. The discontinuous transition in the ![]() [K]
[K]
region from ![]() to
to ![]() is the consequence of the change from the condensed gas structure of the single quantum state of a BEC to the gaseous state of a collection of freely moving particles; this can only be treated with quantum mechanics (in a BEC experiment the energy
is the consequence of the change from the condensed gas structure of the single quantum state of a BEC to the gaseous state of a collection of freely moving particles; this can only be treated with quantum mechanics (in a BEC experiment the energy ![]() is extracted from the mass
is extracted from the mass![]() ). The continuous transition at fixed
). The continuous transition at fixed ![]() from
from ![]() to
to ![]() is thermodynamically treated as a phase transition of the first kind (the complete change from solid to liquid structures requires the energy
is thermodynamically treated as a phase transition of the first kind (the complete change from solid to liquid structures requires the energy ![]() that is called latent heat). The transition at
that is called latent heat). The transition at ![]() from
from ![]() and
and ![]() to
to ![]() is thermodynamically treated as a phase transition of the second kind (the energy to be imparted to the masses
is thermodynamically treated as a phase transition of the second kind (the energy to be imparted to the masses ![]() and
and ![]() vanishes in the limit
vanishes in the limit![]() :
:![]() , i.e. is not latent heat). The smooth and continuous regions
, i.e. is not latent heat). The smooth and continuous regions ![]() aside the circles mark phase transitions between the homogeneous bulks, condensate and vapor. A transition at
aside the circles mark phase transitions between the homogeneous bulks, condensate and vapor. A transition at ![]() from the condensed phase
from the condensed phase ![]() to the vapor phase
to the vapor phase ![]() is likewise classed as a phase transition of the first kind (the vaporization enthalpy
is likewise classed as a phase transition of the first kind (the vaporization enthalpy ![]() has to be provided).
has to be provided).
It is of interest to explain the occurrence of macroscopic fluctuations under the conditions ![]() close to the critical temperature,
close to the critical temperature, ![]() , and their reduction to microscopic fluctuations under the conditions
, and their reduction to microscopic fluctuations under the conditions ![]() for
for![]() . An unstable equilibrium position marks the beginning of decomposition of the mass
. An unstable equilibrium position marks the beginning of decomposition of the mass ![]() to
to ![]() under the condition
under the condition![]() . On a macroscopic scale the binding potential of all particles,
. On a macroscopic scale the binding potential of all particles, ![]() , restricts its averaged value to the averaged value
, restricts its averaged value to the averaged value ![]() at
at![]() . The condition
. The condition ![]() appears twice in the state diagram of a gas (Figure 5): both at high particle number
appears twice in the state diagram of a gas (Figure 5): both at high particle number ![]() and critical density
and critical density ![]() cm
cm![]() in the vicinity of the critical point,
in the vicinity of the critical point, ![]() , and also at low particle number of order
, and also at low particle number of order ![]() and particle densities
and particle densities ![]() cm
cm![]() in the vicinity of the absolute zero,
in the vicinity of the absolute zero,![]() . The state
. The state![]() , as in the case of critical opalescence, is macrocopically described by correlation functions, and the state
, as in the case of critical opalescence, is macrocopically described by correlation functions, and the state![]() , as in the case of a Bose-Einstein condensate, quantum mechanically by a
, as in the case of a Bose-Einstein condensate, quantum mechanically by a
condensate wave function. As already mentioned, correlation functions are a measure of the number of scattering centres for light in the fluid dielectric and hence of a mean value of structural density fluctuations. The strong increase and subsequent decrease of long-wavelength fluctuations in critical fluid regions cause the observed sharp increase and decrease of scattered light intensity (e.g. [13] ) and are thus experimental proof of the thermodynamic zero of the internal energy of, on the one hand, a dense gas in the critical temperature region and, on the other, a dilute-gas in the ![]() K region.
K region.
Evidently, nature associates the problem of changing the sign of ![]() at
at ![]() with the ability of self- organization of particles interacting in ensembles. For
with the ability of self- organization of particles interacting in ensembles. For![]() , the statistically distributed thermal energy of free-moving particles,
, the statistically distributed thermal energy of free-moving particles, ![]() , outweighs the mutual binding energy,
, outweighs the mutual binding energy, ![]() , yielding
, yielding![]() . With decreasing temperature,
. With decreasing temperature, ![]() decreases and
decreases and ![]() becomes more negative, as long as both terms cancel at
becomes more negative, as long as both terms cancel at
![]() , i.e.
, i.e.![]() . The deviation
. The deviation ![]() of the fluctuating energy variable
of the fluctuating energy variable ![]() from its average value
from its average value ![]() is itself a fluctuating variable and the mean square deviation
is itself a fluctuating variable and the mean square deviation ![]() is a convenient measure of the magnitude of the fluctuations [3] . The energy fluctuations become enormously close to the critical point since
is a convenient measure of the magnitude of the fluctuations [3] . The energy fluctuations become enormously close to the critical point since ![]() is equal to
is equal to![]() . Together with density fluctuations, this represents an unstable equilibrium
. Together with density fluctuations, this represents an unstable equilibrium
of the fluid state. One of the best ways of finding solutions for realistic particle interactions under the condition ![]() is to compute the order-parameter probability distribution functions by means of Monte Carlo computer methods [10] . Computer simulations under different thermodynamic conditions afford quite a good picture of the phase transition in the critical region, and in conjunction with the renormalization group techniques allow calculation of critical exponents.
is to compute the order-parameter probability distribution functions by means of Monte Carlo computer methods [10] . Computer simulations under different thermodynamic conditions afford quite a good picture of the phase transition in the critical region, and in conjunction with the renormalization group techniques allow calculation of critical exponents.
For ![]() the Gibbs applied theory, on the other hand, yields with Equations (1)-(5) universal order- parameter relations for calculating material-dependent critical exponents.
the Gibbs applied theory, on the other hand, yields with Equations (1)-(5) universal order- parameter relations for calculating material-dependent critical exponents.
Van der Waals was the first to show that the normalized difference in the phase densities ![]() is empirically very well described by a power law of the form
is empirically very well described by a power law of the form![]() , in which the normalized temperature difference
, in which the normalized temperature difference ![]() appears as a variable and the so-called critical exponent
appears as a variable and the so-called critical exponent ![]() characterizes the decrease of
characterizes the decrease of ![]() as
as ![]() approaches
approaches ![]() (Figure 1). Applied thermodynamics has to determine the particular critical exponent for every order parameter,
(Figure 1). Applied thermodynamics has to determine the particular critical exponent for every order parameter, ![]() and
and![]() , converging to zero. Here the value of the critical exponent depends on the choice of the variable of the order parameter. It is customary to choose the temperature as variable.
, converging to zero. Here the value of the critical exponent depends on the choice of the variable of the order parameter. It is customary to choose the temperature as variable.
When thermodynamic relations between various thermodynamic functions ![]() are known, these will reappear in corresponding relations between their critical exponents. A well-known exponent equation for the saturated fluid (e.g. [7] ) is
are known, these will reappear in corresponding relations between their critical exponents. A well-known exponent equation for the saturated fluid (e.g. [7] ) is
![]() (6)
(6)
(Rushbrooke equation), which describes the numerical relation between the exponents of the reciprocal heat capacity![]() , the difference in the phase-specific volumes
, the difference in the phase-specific volumes![]() , and the reciprocal isothermal compressibility
, and the reciprocal isothermal compressibility![]() . The temperature dependences of these functions in the immediate vicinity of the critical point are defined by
. The temperature dependences of these functions in the immediate vicinity of the critical point are defined by
![]() (7)
(7)
Consequently, the task here is to repeat the calculation of ![]() and
and ![]() and additionally of the exponent of every function, which according to Relations (3) to (5) is connected with the heat capacity. Since
and additionally of the exponent of every function, which according to Relations (3) to (5) is connected with the heat capacity. Since
![]() (8)
(8)
these are the functions![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . Obviously,
. Obviously, ![]() is an important measurable quantity that yields information on the phase transition at
is an important measurable quantity that yields information on the phase transition at![]() . The knowledge obtained about the temperature dependence of the functions mentioned then allows relations between critical exponents to be studied, e.g. between
. The knowledge obtained about the temperature dependence of the functions mentioned then allows relations between critical exponents to be studied, e.g. between![]() ,
, ![]() , and
, and ![]() (Sections 4-9). It is found that only a single independent critical exponent is needed to characterize all order parameters, e.g.
(Sections 4-9). It is found that only a single independent critical exponent is needed to characterize all order parameters, e.g. ![]() and the others can be expressed by it. Data for the fluid selected, saturated water, are given in the Appendix.
and the others can be expressed by it. Data for the fluid selected, saturated water, are given in the Appendix.
It remains to consider some essential properties of the above-mentioned free interface surface.
If the condition for forming a free surface between the liquid and vapor phases is given, then there is an interface particle layer, which represents a new equilibrium state described by a minimum internal energy ![]() and simultaneously a maximum entropy
and simultaneously a maximum entropy![]() . Hence formation of the free interface surface lowers the free energy
. Hence formation of the free interface surface lowers the free energy ![]() of the fluid. The relative energy contribution of an interface quantity to the respective system quantity depends on the ratio of the numbers of interacting particles in the interface volume (of the surface area
of the fluid. The relative energy contribution of an interface quantity to the respective system quantity depends on the ratio of the numbers of interacting particles in the interface volume (of the surface area ![]()
times the layer thickness![]() ) and system volume
) and system volume ![]() and is therefore extremely small. Despite the
and is therefore extremely small. Despite the
smallness of the order ![]() and less, surface effects play a role in nature and technology, e.g. the minimization of the free interface surface. The smallness of an interface quantity shows, on the other hand, that ignoring it when studying volume properties of the fluid is completely justified. As the existence of a surface
and less, surface effects play a role in nature and technology, e.g. the minimization of the free interface surface. The smallness of an interface quantity shows, on the other hand, that ignoring it when studying volume properties of the fluid is completely justified. As the existence of a surface ![]() does not change the mass
does not change the mass ![]() and volume
and volume![]() , the property of
, the property of![]() ,
, ![]() , and
, and ![]() being extensive quantities is maintained.
being extensive quantities is maintained.
If the area-specific difference of the internal energy ![]() is denoted by the temperature coefficient
is denoted by the temperature coefficient ![]() (surface energy), then the coefficient of the surface entropy increased at constant temperature,
(surface energy), then the coefficient of the surface entropy increased at constant temperature, ![]() , is assigned to the function
, is assigned to the function ![]() and that of the surface free energy decreased,
and that of the surface free energy decreased, ![]() , to
, to![]() , yielding the two-phase fluid-relations for
, yielding the two-phase fluid-relations for![]() :
:
![]() (9)
(9)
Equations (9) give![]() ,
, ![]() , and
, and ![]() as functions of the system variables
as functions of the system variables![]() ,
, ![]() , and
, and ![]() and their conjugate temperature variables
and their conjugate temperature variables![]() ,
, ![]() , and
, and![]() . In order to establish a relation between the unknown function
. In order to establish a relation between the unknown function ![]() and the measurable surface tension
and the measurable surface tension![]() , it is posssible simply to identify the negative values
, it is posssible simply to identify the negative values ![]() with the free energy,
with the free energy,
i.e.![]() . It is found that this choice gives the acceptable result of interface- specific coefficients, viz.
. It is found that this choice gives the acceptable result of interface- specific coefficients, viz.![]() ,
, ![]() , and concave curvature
, and concave curvature![]() , as shown in Figure 6 for water. The physical significance of
, as shown in Figure 6 for water. The physical significance of
the negativity of ![]() and
and ![]() and the positivity of
and the positivity of ![]() is readily apparent since these functions multiplied by
is readily apparent since these functions multiplied by ![]() represent area-contributions to the negative internal and free energies and positive entropy of the two-phase fluid.
represent area-contributions to the negative internal and free energies and positive entropy of the two-phase fluid.
3. Vapor Pressure
The experimental finding that the heat capacity diverges at the critical point calls for a statement on the critical behavior of the vapor pressure and chemical potential, since![]() . What was known about the properties of these two quantities at the time when systematic investigations of the critical behavior of fluids and magnets were initiated [14] -[17] is summarized by Stanley [7] in his book (1971), Introduction to phase transitions and critical phenomena, as follows: If
. What was known about the properties of these two quantities at the time when systematic investigations of the critical behavior of fluids and magnets were initiated [14] -[17] is summarized by Stanley [7] in his book (1971), Introduction to phase transitions and critical phenomena, as follows: If ![]() is divergent, then
is divergent, then ![]() or
or ![]() or both will be divergent. The exponent
or both will be divergent. The exponent ![]() is introduced as a measure of the degree of divergence (if any) of the curvature of the vapor pressure curve, i.e.
is introduced as a measure of the degree of divergence (if any) of the curvature of the vapor pressure curve, i.e.![]() . The lattice-gas model gives
. The lattice-gas model gives![]() . However, for the real gas the curvatures of
. However, for the real gas the curvatures of ![]() and
and ![]() might both indicate divergence, so that
might both indicate divergence, so that ![]() might differ from
might differ from![]() . In particular, the divergence of the heat capacity of helium-4 (
. In particular, the divergence of the heat capacity of helium-4 (![]() He) appears to be dominated by
He) appears to be dominated by
![]() rather than by
rather than by![]() .
.
Since then investigators have become resigned to not making any statement on ![]() and letting
and letting ![]() grow as
grow as ![]() (e.g. [18] -[22] ). This attitude, however, is not accepted by all. In general, the literature provides no uniform statement on the temperature dependence of
(e.g. [18] -[22] ). This attitude, however, is not accepted by all. In general, the literature provides no uniform statement on the temperature dependence of ![]() in the critical region. The findings range from the absence of divergence, e.g. in the case of helium-3, to explicit specification of the exponent, e.g.
in the critical region. The findings range from the absence of divergence, e.g. in the case of helium-3, to explicit specification of the exponent, e.g. ![]() in the case of water [4] [5] .
in the case of water [4] [5] .
We shall take up the problem and show that![]() . If, on the other hand, the exponent
. If, on the other hand, the exponent ![]() is introduced in order to describe by
is introduced in order to describe by ![]() the divergence of the curvature of the two-phase chemical potential, then
the divergence of the curvature of the two-phase chemical potential, then ![]() is valid, as shown in Section 7.
is valid, as shown in Section 7.
In the one-phase critical region ![]() a distinction must be made between conditions at constant volume, pressure, and chemical potential since
a distinction must be made between conditions at constant volume, pressure, and chemical potential since![]() ,
, ![]() , and
, and![]() . For example, the difference of the heat capacities is positive,
. For example, the difference of the heat capacities is positive, ![]() , while it vanishes in the case of the two-phase fluid
, while it vanishes in the case of the two-phase fluid ![]() [11] . To describe phase transitions under various conditions at
[11] . To describe phase transitions under various conditions at ![]() it is necessary to introduce some different independent critical exponents that are inter-related [10] [23] -[27] .
it is necessary to introduce some different independent critical exponents that are inter-related [10] [23] -[27] .
With respect to the vapor pressure, the necessary thermodynamic proof of the finiteness of ![]() in the critical region enlists the possibility of estimating the second temperature derivative by an expression containing as highest temperature derivative the first derivative
in the critical region enlists the possibility of estimating the second temperature derivative by an expression containing as highest temperature derivative the first derivative![]() , which itself is finite at the critical point. An estimate formula is obtained as follows. The vapor pressure can be expressed by the following relations:
, which itself is finite at the critical point. An estimate formula is obtained as follows. The vapor pressure can be expressed by the following relations:
![]() , (10)
, (10)
![]() .
.
The function ![]() is defined by the ratio of the evaporation energy
is defined by the ratio of the evaporation energy ![]() to the volume energy
to the volume energy ![]() at the phase transition. This ratio, which is always greater than 1, decreases monotonically as the temperature rises because the binding energy difference
at the phase transition. This ratio, which is always greater than 1, decreases monotonically as the temperature rises because the binding energy difference![]() , although its contribution to the heat of vaporization,
, although its contribution to the heat of vaporization, ![]() , always exceeds that of the free energy difference
, always exceeds that of the free energy difference![]() , continuously decreases with rising temperature in proportion to
, continuously decreases with rising temperature in proportion to![]() . In other words, the function
. In other words, the function ![]() decreases with increasing
decreases with increasing![]() :
:
![]()
Differentiating Equation (10) gives ![]() and
and ![]() . The term of interest here is
. The term of interest here is ![]() . In the critical region the quotient
. In the critical region the quotient ![]() has a well- defined value which does not essentially change in the limits
has a well- defined value which does not essentially change in the limits ![]() and
and ![]() and can thus already be determined at a great distance from the critical point. It is finite and almost constant in the entire critical region.
and can thus already be determined at a great distance from the critical point. It is finite and almost constant in the entire critical region.
From ![]() in the critical region it follows that
in the critical region it follows that ![]() and, because of
and, because of ![]() for
for![]() , the following etimate is generally valid:
, the following etimate is generally valid:
![]() (11)
(11)
The maximum value of ![]() is assumed at the critical point and is finite; it is thus shown that
is assumed at the critical point and is finite; it is thus shown that ![]() never diverges.
never diverges.
It will now be shown that no temperature derivative of the vapor pressure diverges at the critical point, where it holds that![]() ; this value can be calculated according to the scaling laws
; this value can be calculated according to the scaling laws ![]() and
and ![]() and with
and with ![]() is finite; the critical value
is finite; the critical value ![]() is likewise finite. Since
is likewise finite. Since ![]() scales as
scales as![]() , further differentiation of
, further differentiation of ![]() cannot generate a divergent term and always yields on the left-hand side a term with a derivative of
cannot generate a divergent term and always yields on the left-hand side a term with a derivative of ![]() one degree higher than on the right-hand side, which only contains terms whose values at the critical point are finite. Since, therefore, every derivative
one degree higher than on the right-hand side, which only contains terms whose values at the critical point are finite. Since, therefore, every derivative ![]() can be expressed by terms
can be expressed by terms ![]() with
with ![]() which do not diverge at
which do not diverge at![]() ,
, ![]() does not diverge either. From this it follows that
does not diverge either. From this it follows that ![]() can be expanded about the critical point as a Taylor series.
can be expanded about the critical point as a Taylor series.
Series expansion of ![]()
Since the derivatives ![]() exist for every integer
exist for every integer ![]() and do not diverge, the temperature expansion of
and do not diverge, the temperature expansion of ![]() around
around ![]() is possible, yielding
is possible, yielding
![]() . (12)
. (12)
The ![]() -expansion (where
-expansion (where ![]() and
and![]() ) reads
) reads
![]() . (13)
. (13)
The positive functions ![]() and
and ![]() increase monotonically as the temperature up to their finite critical values
increase monotonically as the temperature up to their finite critical values ![]() and
and![]() , i.e. it holds that
, i.e. it holds that ![]() and
and ![]() for
for![]() . The constants
. The constants ![]() in the
in the ![]() -expansion are found by fitting the given vapor pressure data
-expansion are found by fitting the given vapor pressure data![]() .
.
A fit formula of conceptually different form, based on the expression (10) for the vapor pressure, is
![]() , (14)
, (14)
where ![]() and
and ![]() are reference values, e.g. the boiling temperature
are reference values, e.g. the boiling temperature ![]() [K] at atmospheric pressure
[K] at atmospheric pressure ![]() [MPa].
[MPa].
The usual representation of measured vapor pressure data ![]() in the form
in the form ![]() versus
versus ![]() shows that
shows that
the data can be described in first approximation by the straight line through the boundary points ![]() and
and ![]() (see Figure 7). This linear function is
(see Figure 7). This linear function is
![]() . (15)
. (15)
If one introduces the dimensionless variable ![]() instead of the inverse temperature variable
instead of the inverse temperature variable![]() ,
, ![]() is represented as a function of
is represented as a function of ![]() as follows:
as follows:
![]() (16)
(16)
The essential property of the function ![]() is that the derivatives
is that the derivatives ![]() exist
exist
for arbitrary ![]() and remain finite for
and remain finite for![]() . This satisfies the above-stated thermodynamic requirements, viz. that
. This satisfies the above-stated thermodynamic requirements, viz. that ![]() may nowhere diverge in
may nowhere diverge in![]() . Fine fitting with measured vapor pressure data
. Fine fitting with measured vapor pressure data ![]() calls for a further function
calls for a further function![]() , which, of course, is likewise arbitrarily often differentiable and nowhere diverges, and which together with
, which, of course, is likewise arbitrarily often differentiable and nowhere diverges, and which together with ![]() as product function
as product function ![]() fits the values
fits the values![]() . As a function with
. As a function with ![]() fit constants
fit constants![]() , the finite power series
, the finite power series
![]() (17)
(17)
can perform the task required.
The first three derivatives of ![]() are
are![]() ,
, ![]() and
and![]() . The
. The ![]() -th derivative is
-th derivative is![]() .
.
If the ![]() -th derivatives of
-th derivatives of ![]() and
and ![]() are denoted for short by
are denoted for short by ![]() and
and![]() , the
, the ![]() -th derivative of
-th derivative of ![]() is
is
![]() (18)
(18)
With the binomial coefficients![]() , i.e. the figures in the Pascal triangle, one can calculate all
, i.e. the figures in the Pascal triangle, one can calculate all ![]() derivatives of the function
derivatives of the function ![]() and they are all finite in
and they are all finite in![]() .
.
The following fit formula for the vapor pressure is conceived such, with due allowance for Equation (10), that it does not yield any divergent higher-order temperature derivative:
![]() (19)
(19)
Each constant ![]() of the series
of the series ![]() (see Equation (17)) is multiplied by the prefactor
(see Equation (17)) is multiplied by the prefactor ![]()
of ![]() (see Equation (16)), yielding the constant
(see Equation (16)), yielding the constant![]() , which is again denoted by
, which is again denoted by ![]() in the fit formula (19). Equation (19) can be used for describing the vapor pressure of every fluid. In the literature, however, one finds fit equations (e.g. in [4] [5] [22] ) that are thermodynamically incorrect, because the corresponding function
in the fit formula (19). Equation (19) can be used for describing the vapor pressure of every fluid. In the literature, however, one finds fit equations (e.g. in [4] [5] [22] ) that are thermodynamically incorrect, because the corresponding function ![]() contains terms with non-integer exponents
contains terms with non-integer exponents ![]() (e.g. terms such as
(e.g. terms such as ![]() or
or![]() ) that lead to divergences of
) that lead to divergences of
![]() for.
for.
Formula (19) with the ten fit constants listed in the Appendix, Equation (A3), reproduces the measured data ![]() of water with the same accuracy as that given in [4] -[6] . The calculations of
of water with the same accuracy as that given in [4] -[6] . The calculations of ![]() in this study and, on the other hand, according to the equations published in [4] and [5] show that the differences expected occur exactly in the critical region, as seen in Figure 7. Results of calculating the water vapor pressure
in this study and, on the other hand, according to the equations published in [4] and [5] show that the differences expected occur exactly in the critical region, as seen in Figure 7. Results of calculating the water vapor pressure ![]() according to Equations (13), (14), and (19) are given in the Appendix (fit functions (1)-(3)).
according to Equations (13), (14), and (19) are given in the Appendix (fit functions (1)-(3)).
4. Coexistence Curve
Along the coexistence curve in the critical region, the scaling laws must of course obey each two-phase equilibrium relation, e.g.![]() , and at the critical temperature
, and at the critical temperature ![]() the limits [11] :
the limits [11] :
![]() (20)
(20)
In accordance with the defining Equation (7) for the exponent ![]() one obtains the scaling laws of the phase- specific volumes, internal energies and entropies in relation to their critical values as follows:
one obtains the scaling laws of the phase- specific volumes, internal energies and entropies in relation to their critical values as follows:
![]() (21)
(21)
In these formulae the plus sign refers to the vapor phase and the minus sign to the liquid phase. According to van der Waals the temperature dependences of the volumes ![]() and
and ![]() can be represented as series expansions about the critical value
can be represented as series expansions about the critical value![]() , where the temperature expansion variable
, where the temperature expansion variable ![]() gives the distance to the critical point and at the same time the decrease of the difference
gives the distance to the critical point and at the same time the decrease of the difference![]() , which both tend to zero on approaching the critical point:
, which both tend to zero on approaching the critical point:
![]() (22)
(22)
The expansion variable ![]() is then expressed by the power function
is then expressed by the power function
![]() (23)
(23)
The temperature dependence of ![]() is described by
is described by![]() ,
, ![]() is a positive constant, and
is a positive constant, and ![]() is the
is the
exponent defined by the function under consideration, for example, ![]() for the functions
for the functions![]() . The definition range
. The definition range ![]() for
for ![]() and
and ![]() restricts the range of values of
restricts the range of values of ![]() and
and![]() . For
. For
saturated fluids one has ![]() and
and ![]() can assume a positive or negative value. The smaller a positive exponent
can assume a positive or negative value. The smaller a positive exponent ![]() is, the deeper the approach of the function to zero. A negative
is, the deeper the approach of the function to zero. A negative ![]() corresponds to a function which diverges to infinity at the critical point. An exponent
corresponds to a function which diverges to infinity at the critical point. An exponent ![]() leads to a series expansion with no anomalous behavior as, for example, the vapor-pressure difference
leads to a series expansion with no anomalous behavior as, for example, the vapor-pressure difference ![]() in Equation (13). The properties stated are also exhibited according to Equation (21) by the functions
in Equation (13). The properties stated are also exhibited according to Equation (21) by the functions ![]() and
and![]() , where
, where![]() .
.
5. Critical Exponents of the Phase-Specific Quantities ![]() and
and ![]()
According to Equation (3) a quotient ![]() has a finite value
has a finite value ![]() at every temperature
at every temperature![]() . It thus follows that
. It thus follows that
![]() (24)
(24)
According to Landau every quantity ![]() between the stable phase-limiting values
between the stable phase-limiting values ![]() and
and![]() , whose difference, as described in Equation (24), tends to zero on approaching the critical state
, whose difference, as described in Equation (24), tends to zero on approaching the critical state![]() , is based on an order parameter [28] . In the case of the saturated fluid the natural order parameter is the difference of the
, is based on an order parameter [28] . In the case of the saturated fluid the natural order parameter is the difference of the
condensation and vapor masses in relation to the fluid mass,![]() . The ratios
. The ratios ![]() and
and ![]() can be expressed by the quotients
can be expressed by the quotients ![]() and
and![]() . If the value
. If the value ![]() in
in ![]() is expressed by
is expressed by![]() , which is justified in the critical region (see curves 1 and [1] in Figure 8), then
, which is justified in the critical region (see curves 1 and [1] in Figure 8), then ![]() is identical to
is identical to![]() .
.
The variable ![]() thus represents the order parameter of the mass splitting, which as natural order parameter of the two-phase fluid is also the basis of all other order parameters:
thus represents the order parameter of the mass splitting, which as natural order parameter of the two-phase fluid is also the basis of all other order parameters:
![]() (25)
(25)
For values![]() , the phase-specific volumes and internal energies on the coexistence curve conform to the scaling functions,
, the phase-specific volumes and internal energies on the coexistence curve conform to the scaling functions,
![]() (26)
(26)
The values of ![]() and
and ![]() can be determined empirically by varying them until the curves of the published data (curves 2 and 3) and the scaling laws (straight lines [2] [3] ) satisfactorily converge in the critical region as shown
can be determined empirically by varying them until the curves of the published data (curves 2 and 3) and the scaling laws (straight lines [2] [3] ) satisfactorily converge in the critical region as shown
for water in Figure 8. From Figure 9 it is seen that relations (26) are valid for ![]() and hence for
and hence for![]() . One obtains
. One obtains![]() ,
, ![]() ,
, ![]() ,
,![]() . With
. With ![]() one gets
one gets![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
It can now be stated that the phase-specific quantities ![]() and
and ![]() in relation to their critical value
in relation to their critical value ![]() scale as
scale as![]() :
:
![]() (27)
(27)
In contrast, the temperature derivatives ![]() scale as
scale as![]() ; they diverge at the critical point where
; they diverge at the critical point where ![]() because
because![]() :
:
![]() (28)
(28)
Calculation of ![]() and
and ![]() yields with
yields with ![]()
![]() (29)
(29)
The relation![]() , claimed by Ref. [11] , is wrong and must be replaced by Equation (29). The divergence
, claimed by Ref. [11] , is wrong and must be replaced by Equation (29). The divergence ![]() also follows from
also follows from
![]() and
and
![]() .
.
To get temperature-dependent quantities in the entire temperature range of the liquid![]() , the given data
, the given data ![]() and
and ![]() are fitted and represented as power series. Here
are fitted and represented as power series. Here ![]() is chosen as
is chosen as
independent variable with values between 0 and 1, and ![]() is replaced by
is replaced by![]() . A fit function expanded about the critical point with the exponent
. A fit function expanded about the critical point with the exponent ![]() is then
is then
![]() (30)
(30)
The sum contains ![]() constants
constants ![]() which are specific to the quantity to be fitted and are calculated by the mathematical method of conjugate gradients by fitting the given data. Quantities such as the vapor functions
which are specific to the quantity to be fitted and are calculated by the mathematical method of conjugate gradients by fitting the given data. Quantities such as the vapor functions
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and the corresponding liquid functions as well as the differences
and the corresponding liquid functions as well as the differences ![]() are expressed in terms of the fit function (30). It is found that
are expressed in terms of the fit function (30). It is found that ![]() constants is
constants is
sufficient to generate data with the numerical exactness usual in the literature. Results are stated in the Appendix, see fit functions (5)-(26).
6. Critical Exponent of the Fluid Energy
First it is shown that the internal energy is an order parameter:
![]()
At ![]() one has
one has ![]() and
and ![]() [11] , i.e.
[11] , i.e.![]() .
.
Each of the following functions has the property of an order parameter since it holds that![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
To obtain the fluid quantity ![]() as a function of
as a function of![]() , Relation (2) is transformed as follows:
, Relation (2) is transformed as follows:
![]() (31)
(31)
The fluid quantity ![]() in relation to its critical value
in relation to its critical value ![]() (which takes either the minimum or maximum of
(which takes either the minimum or maximum of![]() ) scales as
) scales as![]() :
:
![]() (32)
(32)
In the case ![]() one obtains with
one obtains with ![]()
![]() (33)
(33)
Below![]() ,
, ![]() is a negative function which tends to zero in the critical region as
is a negative function which tends to zero in the critical region as ![]() or
or![]() . The temperature derivative
. The temperature derivative ![]() is a positive function and scales as
is a positive function and scales as![]() :
:
![]() (34)
(34)
For![]() ,
, ![]() diverges as
diverges as![]() .
.
Quantities such as the fluid functions![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are fitted by the fit function
are fitted by the fit function
![]() (35)
(35)
See Appendix, fit functions (27)-(33). In particular, from ![]() one has, because of
one has, because of ![]() and
and ![]() [16] , the scaling
[16] , the scaling![]() .
.
7. Critical Exponents of the Heat Capacity and Chemical Potential Functions
The scaling of![]() , taking Relations (4) and (26) into account, is calculated as follows:
, taking Relations (4) and (26) into account, is calculated as follows:
![]() (36)
(36)
Thus, ![]() tends to the final value
tends to the final value![]() , while the difference
, while the difference ![]() converges to zero as
converges to zero as![]() :
:
![]() (37)
(37)
This agrees with Equation (5). Differentiation of ![]() yields
yields
![]() (38)
(38)
The scalings of ![]() and
and ![]() are with
are with ![]() described by Equation (34) and the scaling of
described by Equation (34) and the scaling of ![]() is calculated from the difference
is calculated from the difference![]() :
:
![]() (39)
(39)
The (positive) functions ![]() and
and ![]() diverge for
diverge for ![]() as
as![]() , while the (negative) function
, while the (negative) function ![]() converges as
converges as ![]() to 0. The exponent of
to 0. The exponent of ![]() is denoted in accordance with Equation (7) by
is denoted in accordance with Equation (7) by![]() ; is thus holds that
; is thus holds that![]() . The identity
. The identity
![]() (40)
(40)
thus states that the heat capacity function ![]() is the temperature derivative of the internal energy function
is the temperature derivative of the internal energy function![]() , whose exponent is
, whose exponent is![]() . From the scaling
. From the scaling ![]() it follows that the function
it follows that the function ![]() converges to zero as
converges to zero as ![]() and the function
and the function ![]() as
as![]() , where
, where ![]() are constants. See Appendix, fit functions (38) and (39).
are constants. See Appendix, fit functions (38) and (39).
8. Critical Exponent of the Reciprocal Isothermal Compressibility of the Two-Phase Fluid
The isothermal compressibility ![]() is measured as the relative change of the fluid volume when the pressure is increased, i.e. the reciprocal isothermal compressibility
is measured as the relative change of the fluid volume when the pressure is increased, i.e. the reciprocal isothermal compressibility ![]() is defined by the relations:
is defined by the relations:
![]() (41)
(41)
In the one-phase region the density ![]() and pressure
and pressure ![]() increase monotonically along an isotherm
increase monotonically along an isotherm ![]() and one gets the relations
and one gets the relations ![]() with the value
with the value ![]() at the critical point [14] . In the two-phase region, on the other hand, the vapor pressure
at the critical point [14] . In the two-phase region, on the other hand, the vapor pressure ![]() and densities
and densities ![]() remain constant at constant temperature, and one has to consider how a mechanical quantity such as the isothermal compressibility is to be interpreted here. Any attempt to compress the fluid of constant density
remain constant at constant temperature, and one has to consider how a mechanical quantity such as the isothermal compressibility is to be interpreted here. Any attempt to compress the fluid of constant density ![]() is accompanied by condensation of the vapor mass
is accompanied by condensation of the vapor mass ![]() and release of energy
and release of energy![]() , which results in a temperature increase by
, which results in a temperature increase by![]() , this in turn leading to the pressure increase
, this in turn leading to the pressure increase![]() . The isothermal compressibility is therefore infinite except on the coexistence boundary when the fluid becomes homogeneous on the liquid side. Representation of the connection between vapor pressure and phase densities along the coexistence curve allows the difference
. The isothermal compressibility is therefore infinite except on the coexistence boundary when the fluid becomes homogeneous on the liquid side. Representation of the connection between vapor pressure and phase densities along the coexistence curve allows the difference ![]() to be introduced as a density function
to be introduced as a density function![]() , whose pressure dependence
, whose pressure dependence ![]() is a well-defined negative quantity with the reciprocal value
is a well-defined negative quantity with the reciprocal value ![]() at the critical point.
at the critical point.
Justification for choosing ![]() and
and ![]() can be given by treating the isothermal compressibility
can be given by treating the isothermal compressibility ![]() according to the Le Ch
according to the Le Ch![]() telier-Braun princple [3] . The change of state
telier-Braun princple [3] . The change of state ![]() is described as the two infinitesimal changes of states, viz.
is described as the two infinitesimal changes of states, viz. ![]() and
and![]() , which process simultaneously and are indirectly induced since
, which process simultaneously and are indirectly induced since![]() . The change of state,
. The change of state, ![]() , is an isothermal variation of the entropy and volume,
, is an isothermal variation of the entropy and volume, ![]() , which according to Equation (3) is expressed by the isothermal phase transition
, which according to Equation (3) is expressed by the isothermal phase transition![]() . The isobaric volume compression,
. The isobaric volume compression, ![]() , is expressed by
, is expressed by![]() . The change
. The change ![]() is the result of the temperature increase
is the result of the temperature increase ![]() or the vapor pressure increase
or the vapor pressure increase ![]() since
since![]() . Hence the effect of the isothermal and isobaric infinitesimal changes on the two-phase fluid of constant density is
. Hence the effect of the isothermal and isobaric infinitesimal changes on the two-phase fluid of constant density is
![]() (42)
(42)
Calculating the scaling of ![]() gives
gives
![]() (43)
(43)
and yields the exponent ![]() of the two-phase fluid:
of the two-phase fluid:
![]() (44)
(44)
The function ![]() is represented in Figure 10 for the case of water; in the
is represented in Figure 10 for the case of water; in the
critical temperature region it goes asymptotically to zero with the proportionality factor![]() . Measurements of
. Measurements of ![]() under one-phase conditions for water liquid and gas about the critical region are performed by Ref. [29] , yielding
under one-phase conditions for water liquid and gas about the critical region are performed by Ref. [29] , yielding![]() .
.
9. Fit Functions for the Saturated Fluid
To describe important thermodynamic properties of the saturated fluid, fit functions of quantities are set up. A fit function presents an appropriate power series expanded about the critical point and affords the possibility of obtaining fairly reliable information concerning the thermodynamic function. Of course, the exponent of the series is defined by the thermodynamic function. Calculation of the fit constants is done by the least squares method, published and estimated data taken as a basis. Fit functions are evaluated for water data (see Appendix). The tables each (arbitrarily) list 10 fit constants, with the aid of which each temperature value of the
thermodynamic quantity in the region ![]() can then be calculated. As an example, some evaluated functions are represented in Figure 11, viz.
can then be calculated. As an example, some evaluated functions are represented in Figure 11, viz.![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
10. Results and Discussion
The Gibbs theory describes the macroscopic state of matter by means of the quantities![]() ,
, ![]() ,
, ![]() , and
, and ![]()
![]()
Figure 10. Calculation of the reciprocal compressibility of saturated water, ![]() (curve 1, Appendix fit function (4)). The straight line 2 represents the function
(curve 1, Appendix fit function (4)). The straight line 2 represents the function![]() .
.
![]()
Figure 11. Properties of water: Curves 1:![]() , curves 2:
, curves 2:![]() , curve 3:
, curve 3:![]() , curve 4:
, curve 4:![]() , curve 5:
, curve 5:![]() , curve 6:
, curve 6:![]() , curves 7:
, curves 7:![]() . At the critical point, the curves 1, 2, 3 and 4 assume the value 0 and the curves 5, 6 and 7 the value
. At the critical point, the curves 1, 2, 3 and 4 assume the value 0 and the curves 5, 6 and 7 the value![]() . One-phase
. One-phase ![]() above
above ![]() according to Ref. [30] .
according to Ref. [30] .
and thus cannot delve into the microscopic processes of interacting particles which give the structure of matter. Nevertheless, the theory treats the thermodynamic equilibrium of matter correctly, using interrelations between the entropy, internal energy, chemical potential, pressure, and temperature. If an additional parameter, ![]() , is introduced for characterizing the behavior of any thermodynamic quantity under the boundary condition of a reversible isobaric and isothermal transition from the condensate structure to vapor, it follows that this
, is introduced for characterizing the behavior of any thermodynamic quantity under the boundary condition of a reversible isobaric and isothermal transition from the condensate structure to vapor, it follows that this ![]() reveals in all thermodynamic relations relevant to these changes. For the two-phase fluid, the established Gibbs interrelations are summarized by Equations (1)-(5). Equations (8) explicitly show relations between the heat capacity, free energy, entropy, internal energy, vapor pressure plus chemical potential, and phase-specific heats and volumes as functions of the temperature and, consequently, the parameter
reveals in all thermodynamic relations relevant to these changes. For the two-phase fluid, the established Gibbs interrelations are summarized by Equations (1)-(5). Equations (8) explicitly show relations between the heat capacity, free energy, entropy, internal energy, vapor pressure plus chemical potential, and phase-specific heats and volumes as functions of the temperature and, consequently, the parameter![]() . Then a specific quantity is formulated, according to van der Waals, in terms of a power series expanded about the critical point as a function of
. Then a specific quantity is formulated, according to van der Waals, in terms of a power series expanded about the critical point as a function of ![]() and
and![]() , which is called a thermodynamic fit function. It is valid between the critical and triple points. Thermodynamic fit functions
, which is called a thermodynamic fit function. It is valid between the critical and triple points. Thermodynamic fit functions ![]() for 40 two-phases quantities are listed in the Appendix. They are given as functions of the temperature variable
for 40 two-phases quantities are listed in the Appendix. They are given as functions of the temperature variable ![]() and characterized by fit parameter arrays
and characterized by fit parameter arrays ![]() and
and![]() . The figures proposed here are specified for saturated water
. The figures proposed here are specified for saturated water![]() .
.
The critical point is thermodynamically defined by the vanishing value of the internal energy, and this ![]() and Nernst’s
and Nernst’s ![]() allow calculation of all thermodynamic functions with absolute figures and the unique transformation of one plotted projection plane into another.
allow calculation of all thermodynamic functions with absolute figures and the unique transformation of one plotted projection plane into another.
Regarding the scaling on approach to the critical point, it is found that the phase-specific volumes, entropies, and energies are dominated by the critical exponent![]() , and the fluid entropy and energy by
, and the fluid entropy and energy by![]() , while the second temperature derivative of the chemical potential by
, while the second temperature derivative of the chemical potential by![]() , thus determining the divergence of the heat capacity. The second temperature derivative of the vapor pressure converges to a finite value. The difference of phase-specific quantities likewise scales as
, thus determining the divergence of the heat capacity. The second temperature derivative of the vapor pressure converges to a finite value. The difference of phase-specific quantities likewise scales as ![]() and the sum scales as
and the sum scales as![]() .
.
The exponents of the reciprocal heat capacity, ![]() , and reciprocal isothermal compressibility,
, and reciprocal isothermal compressibility, ![]() , calculated for the two-phase fluid are not in conformity with those given in the literature for the one-phase fluid. The corresponding exponents differ since the thermodynamic behavior above and below
, calculated for the two-phase fluid are not in conformity with those given in the literature for the one-phase fluid. The corresponding exponents differ since the thermodynamic behavior above and below ![]() is described by different free energy functions [14] . There are large density fluctuations in the immediate vicinity of the critical point under the condition
is described by different free energy functions [14] . There are large density fluctuations in the immediate vicinity of the critical point under the condition![]() . These unstable fluctuations do not occur under the condition
. These unstable fluctuations do not occur under the condition ![]() and are not the subject of the Gibbs theory, which deduces the thermodynamic stable equilibrium of the macroscopic fluid from the statistics of microscopic fluctuations of its constituents at given total energy.
and are not the subject of the Gibbs theory, which deduces the thermodynamic stable equilibrium of the macroscopic fluid from the statistics of microscopic fluctuations of its constituents at given total energy.
The subject of quantum mechanics is to investigate in detail interactions between particles. There are statistical arguments about the relative likelihood of attractive and repulsive interactions. In particular, one has to consider the possible resonant scattering of particles with different internal degrees of freedom and spin- exchange and dipolar processes [12] . This is all very hard to do, but it may finally provide an explanation for large density and energy fluctuations in a fluid in the vicinity of![]() . On the other hand, atto- and femtosecond laser techniques have made it possible to follow the movements of atoms and study subpicosecond processes in solids and liquids as well as in gases (in and out of the direct light interaction region) [31] .
. On the other hand, atto- and femtosecond laser techniques have made it possible to follow the movements of atoms and study subpicosecond processes in solids and liquids as well as in gases (in and out of the direct light interaction region) [31] .
Almost all significant results produced in the years 1960-1980 were obtained at a time when non-classical thermodynamic behavior of the free energy of the one-phase fluid near the critical point is assumed. The efforts to obtain an equation of state that describes the singularities of the heat capacity and isothermal compressibility in the critical region are to be found in, for example, Refs. [14] -[16] , and [29] . As is shown in this study, however, the scaling laws of the two-phase fluid can be treated on the basis of the classical thermodynamic free energy function if the equilibrium relations between the phase-specific volumes, vapor pressure, chemical potential, and heat capacity are considered. A significant result is thus confirmation of the Rushbrooke equation ![]() for the two-phase fluid. It is satisfied by the van der Waals gas because
for the two-phase fluid. It is satisfied by the van der Waals gas because![]() ,
, ![]() , and
, and![]() , and for the real two-phase gas because
, and for the real two-phase gas because ![]() and
and![]() , with
, with ![]() having a value smaller than
having a value smaller than![]() . Since the exponent of the internal energy
. Since the exponent of the internal energy ![]() is
is![]() , the Rushbrooke equation can be interpreted as the sum of the exponents of the reciprocal heat capacity
, the Rushbrooke equation can be interpreted as the sum of the exponents of the reciprocal heat capacity![]() , internal energy
, internal energy![]() , and reciprocal isothermal compressibility
, and reciprocal isothermal compressibility![]() .
.
The appreciable deviations of the two-phase fluid values calculated here, ![]() and
and ![]() (in case of saturated water
(in case of saturated water![]() ,
,![]() ), in relation to those given for the real one-phase fluid in the literature, e.g. Ref. [23] ,
), in relation to those given for the real one-phase fluid in the literature, e.g. Ref. [23] , ![]() ,
, ![]() , and
, and![]() , are very surprising indeed. Such eminently different results can be explained, as mentioned above, by the statements that the scaling hypothesis, in particular the renormalization group techniques, is valid for one-phase fluids where
, are very surprising indeed. Such eminently different results can be explained, as mentioned above, by the statements that the scaling hypothesis, in particular the renormalization group techniques, is valid for one-phase fluids where ![]() and
and![]() , but is not suitable to represent the behavior of two-phase fluids where
, but is not suitable to represent the behavior of two-phase fluids where ![]() and
and ![]() [11] .
[11] .
Nature reveals the thermodynamic energy zero of a gas at the critical point through the sudden appearance of macroscopic fluctuations in a narrow temperature range ![]() above
above![]() . The critical behavior depends on particle interactions, thus the equilibrium conditions of fluid stability and instability and the size of fluctuations in the vicinity of
. The critical behavior depends on particle interactions, thus the equilibrium conditions of fluid stability and instability and the size of fluctuations in the vicinity of ![]() have to be regarded. The condition
have to be regarded. The condition ![]() means that the positive internal energy contribution of the thermal energy of all fluid particles,
means that the positive internal energy contribution of the thermal energy of all fluid particles, ![]() , balances the negative internal energy contribution of the binding energy of all particles,
, balances the negative internal energy contribution of the binding energy of all particles,![]() . Under the condition
. Under the condition ![]() the inter- particle forces of attraction and repulsion cancel. This leads to an unstable equilibrium of one-phase particles and hence local density fluctuations,
the inter- particle forces of attraction and repulsion cancel. This leads to an unstable equilibrium of one-phase particles and hence local density fluctuations, ![]() , of wavelengths of order
, of wavelengths of order ![]() Å [1] . If, however, the mass
Å [1] . If, however, the mass ![]() in
in ![]() is split up into the condensed mass
is split up into the condensed mass ![]() of overbalanced bound particles with
of overbalanced bound particles with ![]() and into the vapor mass
and into the vapor mass ![]() of overbalanced freely moving particles with
of overbalanced freely moving particles with![]() , then there is no eventuality of macroscopic fluctuations, i.e. the masses
, then there is no eventuality of macroscopic fluctuations, i.e. the masses ![]() and
and ![]() are in stable equilibrium within the subvolumes
are in stable equilibrium within the subvolumes ![]() and
and![]() , respectively. Conditions for macroscopic fluctuations and hence observation of critical opalescence exist near to the critical point where
, respectively. Conditions for macroscopic fluctuations and hence observation of critical opalescence exist near to the critical point where ![]() particles,
particles, ![]() , and
, and
![]() , and close to absolute zero where
, and close to absolute zero where ![]() particles,
particles, ![]() , and
, and ![]() (gaseous state). In the BEC state where macroscopic density fluctuations are suppressed and alone microscopic fluctuations occur,
(gaseous state). In the BEC state where macroscopic density fluctuations are suppressed and alone microscopic fluctuations occur, ![]() yields the condition precedent for the existence of coherent matter waves.
yields the condition precedent for the existence of coherent matter waves.
Changes in the fluid structure take place at phase transitions where the gradient ![]() is not
is not
continuous in the representation ![]() (Figure 5). This is the case at the critical point of the Bose- Einstein condensate when the BEC changes to the dilute gas, at the triple point when the solid continuously melts to liquid, and at the critical point of the fluid when the two phases disappear. The first two phase transitions mentioned are associated with heat input required to alter the fluid structure and are called phase transitions of the first kind, whereas the phase transition at the critical point occurs without additional energy and is called a phase transition of the second kind. Every isothermal transition at
(Figure 5). This is the case at the critical point of the Bose- Einstein condensate when the BEC changes to the dilute gas, at the triple point when the solid continuously melts to liquid, and at the critical point of the fluid when the two phases disappear. The first two phase transitions mentioned are associated with heat input required to alter the fluid structure and are called phase transitions of the first kind, whereas the phase transition at the critical point occurs without additional energy and is called a phase transition of the second kind. Every isothermal transition at ![]() from the condensate to the vapor state, which requires the energy input
from the condensate to the vapor state, which requires the energy input![]() , is a phase transition of the first kind.
, is a phase transition of the first kind.
Adding energy to the fluid increases its entropy and thus the mobility of particles, both being equivalent to a loss of matter structure. This feature can be described by the concept of an order parameter. The “natural” order
parameter of the two-phase fluid is ![]() (Equation (25)), but specific order parameters may be used to specify fit functions, e.g.
(Equation (25)), but specific order parameters may be used to specify fit functions, e.g.![]() ,
, ![]() , and
, and![]() , to describe entropic, energetic or volumetric first-kind phase transitions (see Appendix).
, to describe entropic, energetic or volumetric first-kind phase transitions (see Appendix).
Area-specific order parameters are the surface energy ![]() and surface tension
and surface tension![]() . They describe the effect of particle interactions in the highly inhomogeneous interface layer at the free area
. They describe the effect of particle interactions in the highly inhomogeneous interface layer at the free area ![]() between the homogeneous bulks, condensate and vapor. Since
between the homogeneous bulks, condensate and vapor. Since ![]() is part of the fluid internal energy
is part of the fluid internal energy![]() , which is negative below the critical point,
, which is negative below the critical point, ![]() must be negative and the temperature values can be determined according to Equation (9), if
must be negative and the temperature values can be determined according to Equation (9), if
![]() is set equal to the negative temperature values of
is set equal to the negative temperature values of![]() . As part of the fluid free energy
. As part of the fluid free energy![]() ,
, ![]() lowers the free system energy when the fluid proceeds to a new equilibrium state with an interface layer. Interesting enough, the zeros of the surface energy and surface tension, viz.
lowers the free system energy when the fluid proceeds to a new equilibrium state with an interface layer. Interesting enough, the zeros of the surface energy and surface tension, viz. ![]() and
and ![]() at
at ![]() on approaching the critical point from below, evidently display the disappearance of the free interface surface and through
on approaching the critical point from below, evidently display the disappearance of the free interface surface and through ![]() the occurrence of the thermodynamic internal energy zero of the high-density fluid, since
the occurrence of the thermodynamic internal energy zero of the high-density fluid, since![]() .
.
The thermodynamic internal energy zero of the low-density fluid is the vanishing value ![]() at the critical temperature of the BEC, i.e.
at the critical temperature of the BEC, i.e.![]() . The internal gas energy
. The internal gas energy ![]() is positive above
is positive above ![]() and negative below, when all gas particles suddenly condense into a quantum state (Figure 5, where
and negative below, when all gas particles suddenly condense into a quantum state (Figure 5, where![]() ). The lowest energy
). The lowest energy ![]() is assumed by the quantum state of zero momentum, zero entropy and zero temperature [3] .
is assumed by the quantum state of zero momentum, zero entropy and zero temperature [3] .
Acknowledgements
The author would like to thank the Max Planck Institute of Plasma Physics (IPP), Garching, for providing computing facilities. He is also grateful to K. Dodds-Eden, D. Düchs, S. Wipf, and H. P. Zehrfeld for helpful discussions and to A. M. Nicol for the English translation.
Cite this paper
AlbrechtElsner, (2014) Thermodynamic Fit Functions of the Two-Phase Fluid and Critical Exponents. Engineering,06,789-826. doi: 10.4236/eng.2014.612076
References
- 1. Stierstadt, K. (1989) Physik der Materie. VCH Verlag, Weilheim, Chapters 3.4, 10.2, 21.1
- 2. Domb, C. (1996) The Critical Point. Taylor & Francis Ltd, London, Chapters 1, 2, 6.2.4
- 3. Callen, H.B. (1960) Thermodynamics. John Wiley & Sons, Chapters 8.1-8.3, 10.4, 15, Equation (7.35).
- 4. Grigull, U. and Schmidt, E. (1989) Properties of Water and Steam in SI Units. Springer-Verlag, Berlin, T,s-Diagram, p. 205, Equation 1.
- 5. Wagner, W. and Pruss, A. (1993) International Equations for the Saturation Properties of Ordinary Water Substance. Revised According to the International Temperature Scale of 1990. Journal of Physical and Chemical Reference Data, 22, 783-787. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. Journal of Physical and Chemical Reference Data, 31 (2002), 387-535.
http://dx.doi.org/10.1063/1.555926
- 6. Kohlrausch, F. (1996) Praktische Physik. Band 3, Teubner Verlag Stuttgart, Tabelle 3.12.
- 7. Stanley, H.E. (1971) Introduction to Phase Transitions and Critical Phenomena. Clarendon Press, Oxford, Chapters 1.1.1, 3.1, 3.4.2, 7.2.
- 8. Liu, Y. and Suzuki, M. (1987) Some New Developments of the Scaling Theory of Transitient Phenomena. Phase Transitions, 10, 303-314.
http://dx.doi.org/10.1080/01411598708215447
- 9. Kadanoff, L.P. (2009) More Is the Same; Phase Transitions and Mean Field Theories. Journal of Statistical Physics, 137, 777-797.
http://dx.doi.org/10.1007/s10955-009-9814-1
- 10. Plascak, J.A. and Martins, P.H.L. (2013) Probability Distribution Function of the Order Parameter: Mixing Fields and Universality. Computer Physics Communications, 184, 259-269
http://dx.doi.org/10.1016/j.cpc.2012.09.014
- 11. Elsner, A. (2012) Applied Thermodynamics of the Real Gas with Respect to the Thermodynamic Zeros of the Entropy and Internal Energy. Physica B: Condensed Matter, 407, 1055-1067.
http://dx.doi.org/10.1016/j.physb.2011.12.118
- 12. Pethick, C.J. and Smith, H. (2004) Bose-Einstein Condensation in Dilute Gases. Cambridge University Press, Cambridge, Chapter 5, Cover Illustration.
- 13. White, J.A. and Maccabee, B.S. (1971) Temperature Dependence of Critical Opalescence in Carbon Dioxide. Physical Review Letters, 26, 1468-1471.
http://dx.doi.org/10.1103/PhysRevLett.26.1468
- 14. Widom, B. (1965) Equation of State in the Neighborhood of the Critical Point. Journal of Chemical Physics, 43, 3898-3905
http://dx.doi.org/10.1063/1.1696618
- 15. Fisher, M.E. (1967) The Theory of Equilibrium Critical Phenomena. Reports on Progress in Physics, 30, 615-730.
http://dx.doi.org/10.1088/0034-4885/30/2/306
- 16. Rehr, J.J. and Mermin, N.D. (1973) Revised Scaling Equation of State at the Liquid-Vapor Critical Point. Physical Review A, 8, 472, Equations 2.8 and 5.5.
- 17. Heller, P. (1967) Experimental Investigations of Critical Phenomena. Reports on Progress in Physics, 30, 731-826.
http://dx.doi.org/10.1088/0034-4885/30/2/307
- 18. Wagner, W. (1973) New Vapour Pressure Measurements for Argon and Nitrogen and a New Method for Establishing Rational Vapour Pressure Equations. Cryogenics, 13, 470-482.
http://dx.doi.org/10.1016/0011-2275(73)90003-9
- 19. Stewart, R.B. and Jacobsen, R.T. (1989) Thermodynamic Properties of Argon. Journal of Physical and Chemical Reference Data, 18.
- 20. Gilgen, R., Kleinrahm, R. and Wagner, W. (1994) Measurement and Correlation of the (Pressure, Density, Temperature) Relation of Argon, II. Saturated-Liquid and Saturated-Vapour Densities and Vapour Pressures Along the Entire Coexistence Curve. Journal of Chemical Thermodynamics, 26, 399-413.
http://dx.doi.org/10.1006/jcht.1994.1049
- 21. Tegeler, Ch., Span, R. and Wagner, W. (1999) A New Equation of State for Argon Covering the Fluid Region for Temperatures from the Melting Line to 700 K at Pressures up to 1000 MPa. Journal of Physical and Chemical Reference Data, 28, 779-850.
http://dx.doi.org/10.1063/1.556037
- 22. Span, R. and Wagner, W. (1996) A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple Point Temperature to 1100 K at Pressures up to 800 MPa. Journal of Physical and Chemical Reference Data, 25, 1509-1596.
http://dx.doi.org/10.1063/1.555991
- 23. Parola, A. and Reatto, L. (1995) Liquid State Theories and Critical Phenomena. Advances in Physics, 44, 211-298, Table 1, Chapter 5.5, Figure 15.
- 24. Zhong, F. and Meyer, H. (1995) Density Equilibration near the Liquid-Vapor Critical Point of a Pure Fluid: Single Phase T > Tc. Physical Review E, 51, 3223-3241.
http://dx.doi.org/10.1103/PhysRevE.51.3223
- 25. Rowlinson, J.S. (1959) Liquids and Liquid Mixtures. Butterworths Scientific Publications, London, Chapter 3.4.
- 26. Mouritsen, O.G. (1984) Computer Studies on Phase Transitions and Critical Phenomena. Springer-Verlag, Amsterdam.
http://dx.doi.org/10.1007/978-3-642-69709-8
- 27. Potton, J.A. and Lanchester, P.C. (1985) Analysis of Critical Specific Heat Data. Phase Transitions, 6, 43-57.
http://dx.doi.org/10.1080/01411598508219890
- 28. Landau, L.D. and Lifshitz, E.M. (1980) Statistical Physics. Part 1, Pergamon Press, Oxford, 449.
- 29. Levelt Sengers, J.M.H. and Greer, S.C. (1972) Thermodynamic Anomalies near the Critical Point of Steam. International Journal of Heat and Mass Transfer, 15, 1865-1886, Figure 4.
- 30. Schomacker, H. (1973) Messungen der inneren Energie und der spezifischen isochoren Warmekapazitat in der Umgebung des kritischen Zustands von Wasser. Thesis Ruhr-Universitat Bochum, Tabelle 1 und 2.
- 31. Milonni, P.W. and Eberly, J.H. (2010) Laser Physics. Wiley & Sons, Hoboken, Chapter 16.
http://dx.doi.org/10.1002/9780470409718
Appendix: Fit Functions for Thermodynamic Properties of a Saturated Fluid in Liquid-Vapor Equilibrium
Computer program for evaluating fit functions
Temperature values of a specific thermodynamic quantity are calculated by calling the IDL-FUNCTION evaluation in an IDL-source program:
![]()
The IDL-FUNCTION evaluation is specified by the label, e.g.![]() , that is relevant to the selected fit function
, that is relevant to the selected fit function![]() , the fit arrays
, the fit arrays ![]() and
and![]() , and the temperature variable
, and the temperature variable ![]() of
of![]() . The general structure of an IDL evaluation function is given below.
. The general structure of an IDL evaluation function is given below.
![]()
In this work the following values are fixed, valid for saturated water:
![]()
In addition, the values
![]()
are specific for calculating an individual thermodynamic fluid quantity. These are listed by![]() . A thermodynamic quantity is thus described by
. A thermodynamic quantity is thus described by![]() ,
, ![]() , and
, and ![]() as a function of the temperature variable
as a function of the temperature variable![]() , where for instance
, where for instance![]() ・findgen (1234)/(1234
・findgen (1234)/(1234![]() 1).
1).
FUNCTION evaluation, k, a, b, x
The fit function ![]() with label=1 evaluates the vapor pressure Equation (13)
with label=1 evaluates the vapor pressure Equation (13)
![]() (A1)
(A1)
![]()
The fit function ![]() with label = 2 evaluates the vapor pressure Equation (14)
with label = 2 evaluates the vapor pressure Equation (14)
![]() (A2)
(A2)
![]()
The fit function ![]() with label = 3 evaluates the vapor pressure Equation (19)
with label = 3 evaluates the vapor pressure Equation (19)
![]() (A3)
(A3)
![]()
Fit functions for saturated water
Each of the fit functions![]() ,
, ![]() ,
, ![]() yields the vapor pressure
yields the vapor pressure
![]()
![]()
![]()
(1-3) vapor pressure [J/cm3] ![]()
![]()
Fit function ![]() yields the reciprocal isothermal compressibility
yields the reciprocal isothermal compressibility
![]()
(4) reciprocal isothermal compressibility [J/cm3] ![]()
Fit function ![]() yields
yields ![]() for quantities (5)-(26).
for quantities (5)-(26).
According to Equation (30), this function calculates functions with exponents![]() .
.
![]() (A4)
(A4)
![]()
![]()
(5) order parameter ![]()
![]()
(6) relative liquid mass ![]()
![]()
(7) liquid volume [cm![]() /g]
/g] ![]()
![]()
(8) vapor volume [cm![]() /g]
/g] ![]()
![]()
(9) vapor volume-pressure energy [J/g] ![]()
![]()
(10) liquid volume-pressure energy [J/g] ![]()
![]()
(11) specific free energies difference [J/g] ![]()
![]()
(12) specific entropies difference [J/(g![]() K)]
K)] ![]()
![]()
(13) specific enthalpies difference [J/g] ![]()
![]()
(14) specific internal energies difference [J/g] ![]()
![]()
(15) specific heats difference [J/(g![]() K)]
K)] ![]()
![]()
(16) vapor density [g/cm![]() ]
] ![]()
![]()
(17) liquid density [g/cm![]() ]
] ![]()
![]()
(18) densities difference [g/cm![]() ]
] ![]()
![]()
(19) vapor internal energy [J/g] ![]()
![]()
(20) liquid internal energy [J/g] ![]()
![]()
(21) vapor enthalpy [J/g] ![]()
![]()
(22) liquid enthalpy [J/g] ![]()
![]()
(23) vapor entropy [J/(g![]() K)]
K)] ![]()
![]()
(24) liquid entropy [J/(g![]() K)]
K)] ![]()
![]()
(25) vapor free energy [J/g] ![]()
![]()
(26) liquid free energy [J/g] ![]()
Fit function ![]() yields
yields ![]() for quantities (27)-(33). According to Equation (35), this function calculates functions with lowest exponent
for quantities (27)-(33). According to Equation (35), this function calculates functions with lowest exponent![]() .
.
![]() (A5)
(A5)
![]()
![]()
(27) densities sum [g/cm![]() ]
] ![]()
![]()
(28) specific internal energies sum [J/g] ![]()
![]()
(29) specific entropies sum [J/(g![]() K)]
K)] ![]()
![]()
(30) entropy [J/(g![]() K)]
K)] ![]()
![]()
(31) internal energy [J/g] ![]()
![]()
(32) free energy [J/g] ![]()
![]()
(33) chemical potential function [J/g] ![]()
Fit function ![]() yields
yields ![]() for quantities (34)-(35). According to Equation (28), this function calculates functions with lowest exponent
for quantities (34)-(35). According to Equation (28), this function calculates functions with lowest exponent![]() .
.
![]() (A6)
(A6)
![]()
Fit function ![]() yields
yields ![]() for quantities (36)-(37). According to Equation (38), this function calculates functions with lowest exponent
for quantities (36)-(37). According to Equation (38), this function calculates functions with lowest exponent![]() .
.
![]() (A7)
(A7)
![]()
![]()
(34) specific heat of vapor [J/(g![]() K)]
K)] ![]()
![]()
(35) specific heat of liquid [J/(g![]() K)]
K)] ![]()
![]()
(36) heat capacity [J/(g![]() K)]
K)] ![]()
![]()
(37) chemical potential function [J/(g![]() K
K![]() )]
)] ![]()
Fit function ![]() yields
yields ![]() for the quantity (38). This function calculates the temperature derivative of the chemical potential
for the quantity (38). This function calculates the temperature derivative of the chemical potential
![]() (A8)
(A8)
![]()
![]()
(38) chemical potential function [J/(g![]() K)]
K)] ![]()
Fit function ![]() yields
yields ![]() for the quantity (39). This function calculates the chemical potential
for the quantity (39). This function calculates the chemical potential
![]() (A9)
(A9)
![]()
![]()
(39) chemical potential function [J/g] ![]()
Fit function ![]() yields
yields ![]() for the quantity (40). This function calculates the surface tension
for the quantity (40). This function calculates the surface tension
![]() (A10)
(A10)
![]()
![]()
(40) surface tension [dyne/cm] or [erg/cm![]() ]
] ![]()



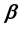 being introduced as the critical exponent for the difference between liquid and vapor densities, it is shown that the critical exponent of each fit function depends (if at all) on
being introduced as the critical exponent for the difference between liquid and vapor densities, it is shown that the critical exponent of each fit function depends (if at all) on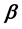 . In particular, the critical exponent of the reciprocal heat capacity
. In particular, the critical exponent of the reciprocal heat capacity 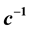 is
is 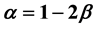 and those of the entropy
and those of the entropy  and internal energy
and internal energy 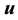 are
are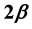 , while that of the reciprocal isothermal compressibility
, while that of the reciprocal isothermal compressibility 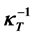 is
is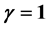 . It is thus found that in the case of the two-phase fluid the Rushbrooke equation conjectured
. It is thus found that in the case of the two-phase fluid the Rushbrooke equation conjectured  combines the scaling laws resulting from the two relations
combines the scaling laws resulting from the two relations 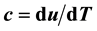 and
and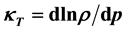 . In the context with
. In the context with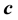 , the second temperature derivatives of the chemical potential
, the second temperature derivatives of the chemical potential 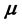 and vapor pressure
and vapor pressure  are investigated. As the critical point is approached,
are investigated. As the critical point is approached, 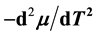 diverges as
diverges as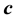 , while
, while 













































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































