Engineering
Vol.6 No.1(2014), Article ID:41892,7 pages DOI:10.4236/eng.2014.61005
Strip Thickness Control of Cold Rolling Mill with Roll Eccentricity Compensation by Using Fuzzy Neural Network
Department of Electrical Engineering, University of Basrah, Basrah, Iraq
Email: waleed_ishaq5@yahoo.com
Received November 12, 2013; revised December 12, 2013; accepted December 19, 2013
ABSTRACT
In rolling mill, the accuracy and quality of the strip exit thickness are very important factors. To realize high accuracy in the strip exit thickness, the Automatic Gauge Control (AGC) system is used. Because of roll eccentricity in backup rolls, the exit thickness deviates periodically. In this paper, we design PI controller in outer loop for the strip exit thickness while PD controller is used in inner loop for the work roll actuator position. Also, in order to reduce the periodic thickness deviation, we propose roll eccentricity compensation by using Fuzzy Neural Network with online tuning. Simulink model for the overall system has been implemented using MATLAB/SIMULINK software. The simulation results show the effectiveness of the proposed control.
Keywords:Cold Rolling Mill; Thickness Control; Roll Eccentricity; Fuzzy Neural Network; Eccentricity Compensation
1. Introduction
Rolling strip is widely used for automobile manufacturing, food packaging, household electric appliances, machinery, light industry, instruments, communications, military affairs and other fields [1]. The design of a controller in the cold rolling system that can improve the behavior and response of the plant to specific performance constraints can be a tedious and challenging problem in many control applications [2]. In order to meet increasing demand for the high precision of strip thickness, various types of Automatic Gauge Control (AGC) methods have been developed for hot or cold mill processes. The British Iron and Steel Research Association (B1SRA) AGC method based on the gauge meter principle and the feed forward AGC method using the delivery time of the strip have been widely utilized in steel rolling mills [3].
Strip products thickness precision is an important quality parameter. But the export thickness appears as the periodical fluctuation in the practical production because of the roll eccentricity thermal expansion of rolls and the fluctuation of the entrance thickness and material stiffness. The mill can be composed of either a single stand or a number of stands where each stand is made up of two back-up rolls and two work rolls. A common problem is the back-up and work rolls are not perfectly circular in shape. In other words, the rolls are eccentric. The roll eccentricity effect will, under normal constant operating forces, result in steel strip with undesirable thickness deviations [1]. Fuzzy logic provides an inference morphology that enables approximate human reasoning capability to be applied in a fuzzy inference system. In recent past, artificial neural network has also played an important role in solving many engineering problems. Neural network has advantages such as learning, adaption, and generalization. Fuzzy systems utilizing the learning capability of neural networks can successfully construct the input-output mapping for many applications [4]. The Fuzzy Neural Network is constructed to merge fuzzy inference mechanism and neural networks into an integrated system so that their individual weaknesses are overcome [5]. In this paper, PI and PD controller has been used to control the output thickness and hydraulic servo system respectively. Also we propose roll eccentricity compensation by using Fuzzy Neural Network. The paper is organized as follows: in Section 2, a brief description of the cold rolling process is presented. In Section 3, a mathematical model has been driven for single-stand cold rolling mill. In Section 4, architecture and learning algorithm of Fuzzy Neural Network have been presented. In Section 5, thickness control with roll eccentricity compensation has been proposed. In Section 6, simulation results have been presented. Finally, section 7 presents the conclusions.
2. Cold Rolling Process Overview
The tandem cold rolling of metal strip is one process in a sequence of processes performed to convert raw materials into a finished product [6]. It is a deformation process in which the thickness of the strip is reduced by compressive forces exerted by two opposing rolls (two or four-high arrangement of rolled products). The roll rotates as illustrated in Figure 1 to pull and simultaneously squeeze the strip between them [7].
The strip is passed through four pairs of independently driven work rolls, with each work roll supported by a backup roll of larger diameter. As the strip passes through the individual pairs of work rolls, the thickness is successively reduced. The reduction in thickness is caused by very high compression stress in a small region (denoted as the roll gap, or the roll bite) between the work rolls. In this region the metal is plastically deformed, and there is slipping between the strip and the work roll surface. The necessary compression force is applied by hydraulic rams, or in many older mills by a screw arrangement driven by an electric motor [6].
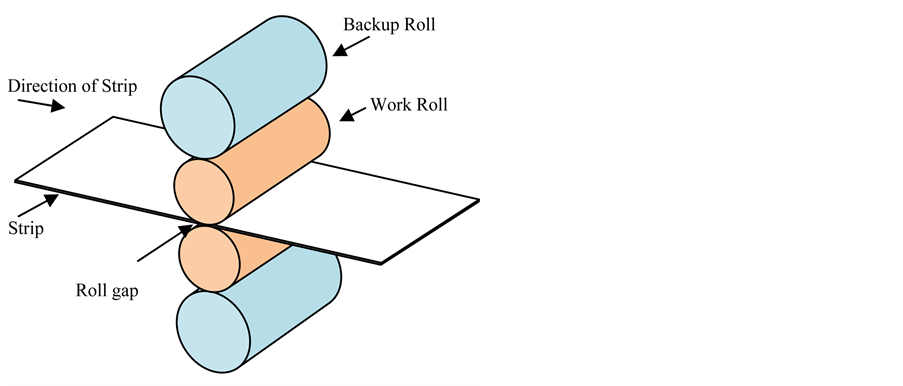
Figure 1. The rolling process (flat rolling).
3. Mathematical Model of Cold Rolling Process
3.1. Force Equation
Define the theory for prediction of specific roll force is central to the development of a model for tandem cold rolling. Referring to Figure 2, which approximately represents the strip in the roll bite area, the incoming strip is of thickness 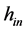 at its centerline and is moving toward the roll bite with speed
at its centerline and is moving toward the roll bite with speed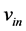 . The strip exits the roll bite with thickness
. The strip exits the roll bite with thickness 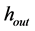 at its centerline and with speed
at its centerline and with speed 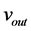 [6,7]. In flat rolling, the strip is squeezed between two rolls so that its thickness is reduced by an amount called the draft [7]:
[6,7]. In flat rolling, the strip is squeezed between two rolls so that its thickness is reduced by an amount called the draft [7]:
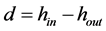 (1)
(1)
where d = draft, mm.
The rolling strip contact length can be approximated by [8]:
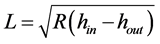 (2)
(2)
The true strain experienced by the strip in rolling is based on before and after stock thickness. In equation form:
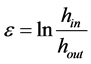 (3)
(3)
The true strain can be used to determine the average flow stress 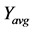 applied to the strip material in flat rolling:
applied to the strip material in flat rolling:
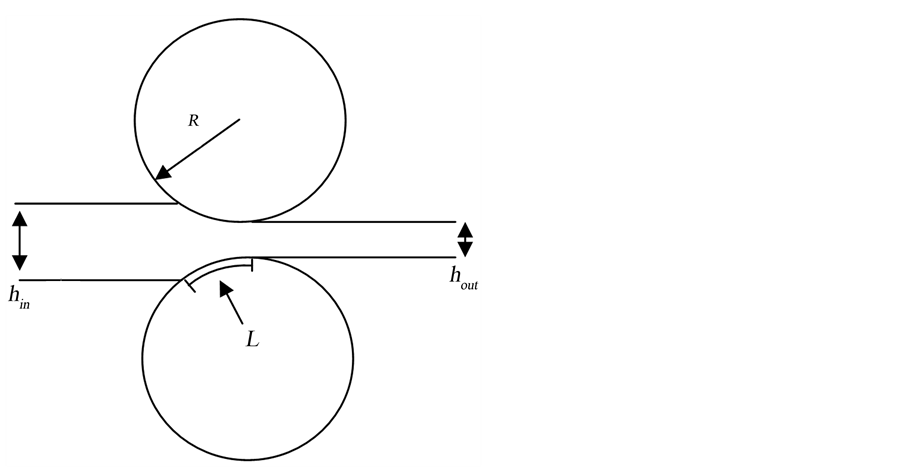
Figure 2. Roll bite area.
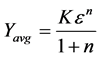 (4)
(4)
where K = the strength coefficient, MPa; and n is the strain hardening exponent.
The force F required to maintain separation between the two rolls can be calculated based on the average flow stress experienced by the strip material in the roll gap [7,8]. That is,
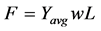 (5)
(5)
where w = width of the strip, R is radius of work roll.
3.2. Output Thickness Equation
In the cold rolling process and the precision is strip thickness of cold rolled strips of key quality products. Conventional Automatic roll gap Control (where Gauge, AGC) system used for Automatic correction strip thickness accuracy [9]. One of the conventional control strategy of strip thickness is using of BISRA measurements to infer strip thickness. This relationship (more often referred to as “gaugemeter” or “BISRA gaugemeter”) has been used to estimate the thickness of the strip exiting the roll bite without requiring a direct measurement. Reliable direct measurement of strip thickness at the exit of the roll bite requires expensive and complex equipment [6]. The relationship between the work roll gap(S), the exit strip thickness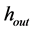 , and the roll force(F) generated at the roll stand is expressed as [3,10]:
, and the roll force(F) generated at the roll stand is expressed as [3,10]:
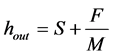 (5)
(5)
where M is mill modulus The BISRA relationship is used to develop a thickness feedback signal for closed-loop control. To control the output thickness, the motion of hydraulic cylinder controlling the roll gap position is such that produces the desired output thickness [6]. Roll eccentricities are caused by axial deviations between the roll barrel and the roll necks due to irregularities in the mill rolls and/or roll bearings [11]. These irregularities cause cyclic deviations in the strip thickness at the output of a mill stand. Figure 3 depicts the effects of eccentricity on the output strip thickness [6].
When the entry strip is passed through the roll stand with the velocity , the disturbance
, the disturbance 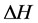 is expressed as:
is expressed as:
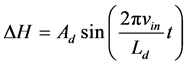 (6)
(6)
where  and
and 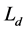 are the magnitude and period of thickness deviation respectively [3]. Roll eccentricity is not part of the controller but must be considered to be consistent with data reported from operating mills which
are the magnitude and period of thickness deviation respectively [3]. Roll eccentricity is not part of the controller but must be considered to be consistent with data reported from operating mills which

Figure 3. Effects of roll eccentricity on output strip thickness.
usually includes its effects. The eccentricity components remaining in the mill exit thickness after compensation. In the model, roll eccentricity modifies Equation (5) as [12]:
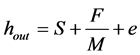 (7)
(7)
where e is the roll eccentricity.
4. Basic Principle of Fuzzy-Neural Network
A promising approach to obtaining the benefits of both fuzzy systems and neural networks and solving their respective problems is to combine them into an integrated system. The integrated system will possess the advantages of both neural networks (e.g., learning abilities, optimization abilities, and connectionist structures) and fuzzy systems (e.g., humanlike IF-THEN rules thinking and ease of incorporating expert knowledge). In this way, we can bring the low-level learning and computational power of neural networks into fuzzy systems and also high-level, humanlike IF-THEN rule thinking and reasoning of fuzzy systems into neural networks. Thus, neural networks can improve their transparency, making them closer to fuzzy systems, while fuzzy systems can self-adapt, making them closer to neural networks. Integrated systems can learn and adapt [13]. The different integrated neurofuzzy models make use of the complementarities of neural networks and fuzzy inference systems implementing a Mamdani or Takagi Sugeno fuzzy inference system [14].
4.1. Architecture of Fuzzy Neural Network (FNN)
The Architecture of FNN shown in Figure 4 [15,16]. FNN considered as a special type of neural network, this means special connection and node operation. Every layer and every node have its practical meaning because the FNN has the structure which is based on both the fuzzy rules and inference [17]. In the following items each layer shown in Figure 4 will be described:
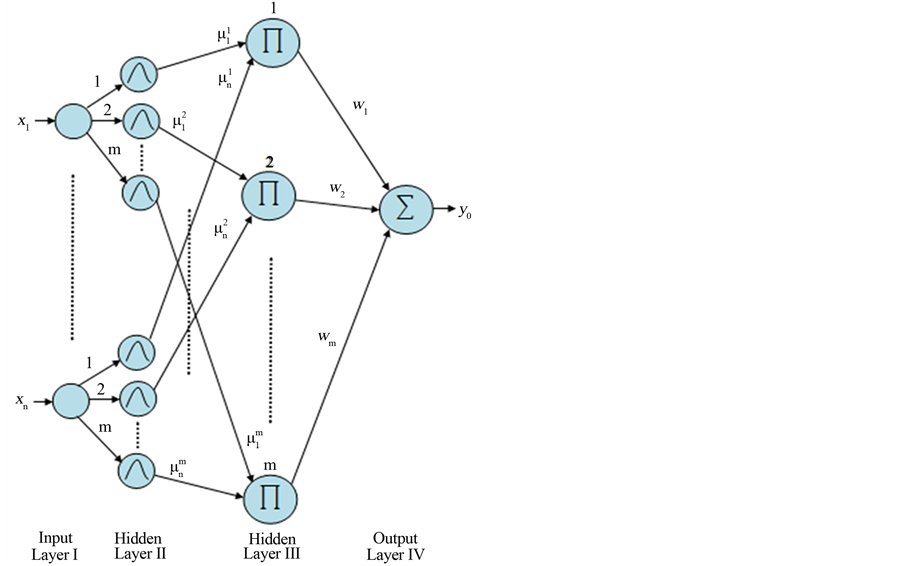
Figure 4. Architecture of FNN.
Input Layer I: Input layer transmits the input linguistic variables 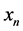 to the output without changed.
to the output without changed.
Hidden Layer II: Membership layer represents the input values with the following Gaussian membership functions [17]:
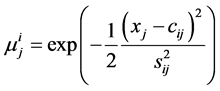 (8)
(8)
where  and
and 
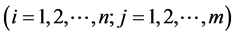 , respectively, are the mean and standard deviation of the Gaussian function in the
, respectively, are the mean and standard deviation of the Gaussian function in the 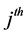 term of the
term of the 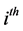 input linguistic variable
input linguistic variable  to the node of this layer.
to the node of this layer.
Hidden Layer III: Rule layer implements the fuzzy inference mechanism, and each node in this layer multiplies the input signals and outputs the result of the product. The output of this layer is given as [17]:
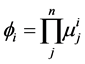 (9)
(9)
where  represent the
represent the 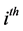 output of rule layer.
output of rule layer.
Output Layer IV: Layer four is the output layer, and nodes in this layer represent output linguistic variables. Each node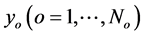 , which computes the output as:
, which computes the output as:
 (10)
(10)
where 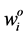 represent the
represent the 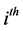 output weight of rule layer.
output weight of rule layer.
4.2. Learning Algorithm for FNN Controller
The parameter of the FNN controller presented in Figure 4 should be adjusted according to the following equations [18]:
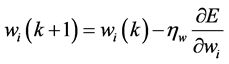 (11)
(11)
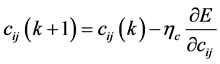 (12)
(12)
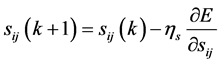 (13)
(13)
The goal of the learning algorithm is to minimize the error between the desired output thickness 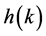 and the output thickness of the stand
and the output thickness of the stand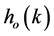 . In the present work the Least Mean Square (LMS) function will be used to define a criterion for the error E.
. In the present work the Least Mean Square (LMS) function will be used to define a criterion for the error E.
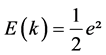 (14)
(14)
 (15)
(15)
where η is the learning rate for each parameter in the system,  and
and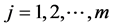 .
.
5. Design of Thickness Control with Roll Eccentricity Compensation
The block diagram of exit thickness control with roll eccentricity compensation is shown in Figure 5. As an inner loop of Hydraulic AGC System, the difference value between desired position roll gap and the real position measured by displacement sensor of hydraulic cylinder is input to APC controller. Automatic position control (APC) can affect the exit thickness by controlling the position of hydraulic cylinder [1]. The main components of hydraulic screw down servo system include controller, servo amplifier, servo valve, hydraulic cylinder, roller system and body of rolling mill, and some sensors [19]. In the outer loop, the difference between desired thickness and output thickness is fed to AGC to give the desired position roll gap. Fuzzy Neural Network system have been used with online training to compensation the effect of roll eccentricity. The first input of the Fuzzy Neural Network system is output thickness and the second input is change of output thickness. The output of the Fuzzy Neural Network system (c) added to the desired position to regulate the roll gap and then reducing the periodic thickness deviation. em is the error between desired output thickness and output thickness of the stand that used as trajectory in adaptive mechanism. SIMULINK model of thickness control have been implemented using MATLAB/SIMULINK software as shown in Figure 6. PI controller is used as AGC and PD controller is
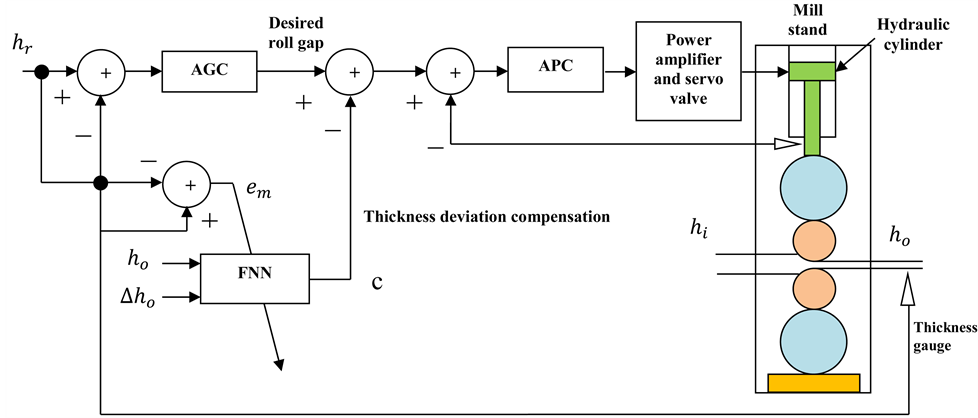
Figure 5. Block diagram of exit thickness control.
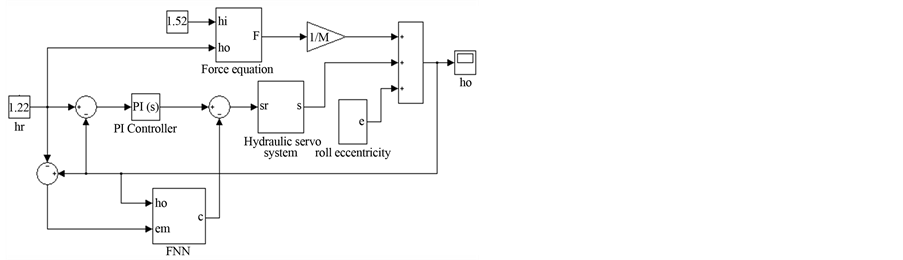
Figure 6. Simulink model of thickness control.
used as APC.
The simulink model of force equation is shown in Figure 7. Also the simulink model of hydraulic servo system is shown in Figure 8 [20].
6. Simulation Results
A program written in Matlab code is used to simulate FNN using Matlab S-function programming. In the primes part, the number of membership functions for each input are five. So, the number of weights in the consequence part is also five. The mill and strip properties is shown in Table1Without roll eccentricity effect, Figure 9 shows the exit thickness when the desired thickness is 1.22 mm. When roll eccentricity is taken into account, the exit thickness is shown in Figure 10. As shown in this figure, the disturbance (∆H) which has Amplitude  appear periodically in the exit thickness and this is drawback that effect on the accuracy and quality of the strip exit thickness. The compensation signal (c) which is produced by FNN added to the desired position roll gap to reduce the periodic deviation in the exit thickness. This is shown clearly in Figure 11 which
appear periodically in the exit thickness and this is drawback that effect on the accuracy and quality of the strip exit thickness. The compensation signal (c) which is produced by FNN added to the desired position roll gap to reduce the periodic deviation in the exit thickness. This is shown clearly in Figure 11 which
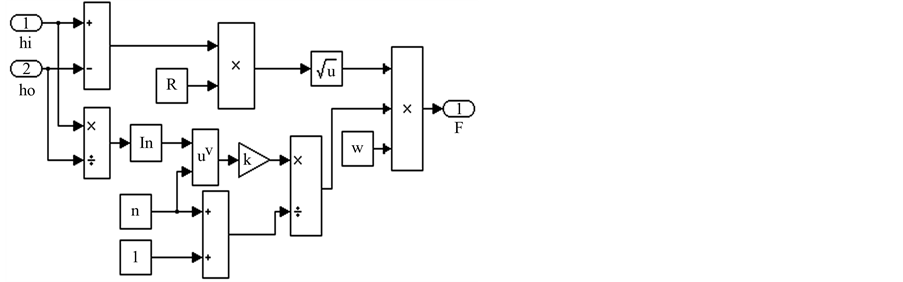
Figure 7. Simulink model of force equation.
shows the exit thickness after cancellation the effect of roll eccentricity. The exit thickness with and without compensation is shown in Figure 12. From simulation

Figure 8. Simulink model of hydraulic servo system.

Figure 9. Exit thickness without roll eccentricity effect.
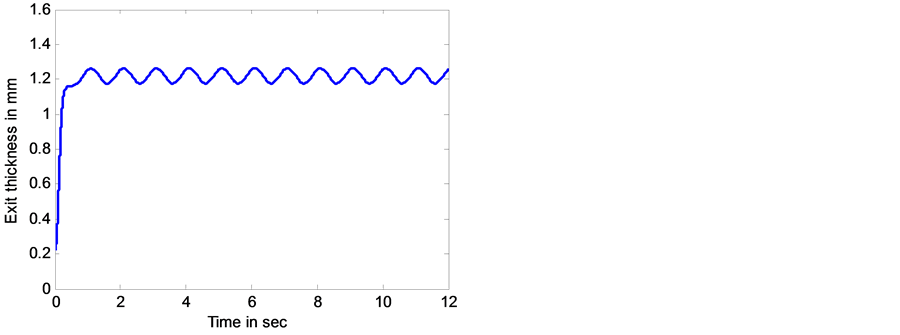
Figure 10. Exit thickness with roll eccentricity effect.
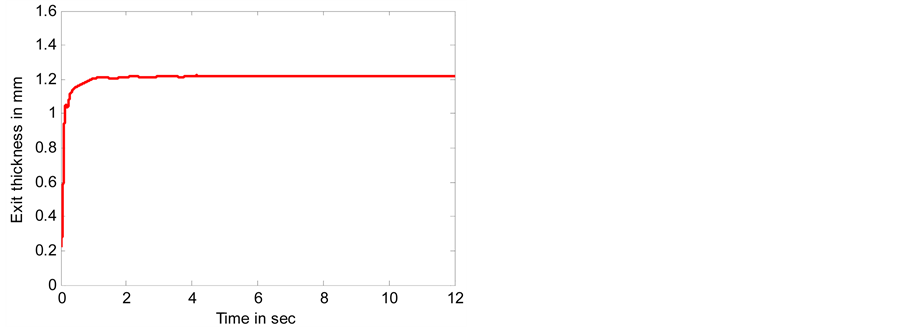
Figure 11. Exit thickness after compensation the effect of roll eccentricity.
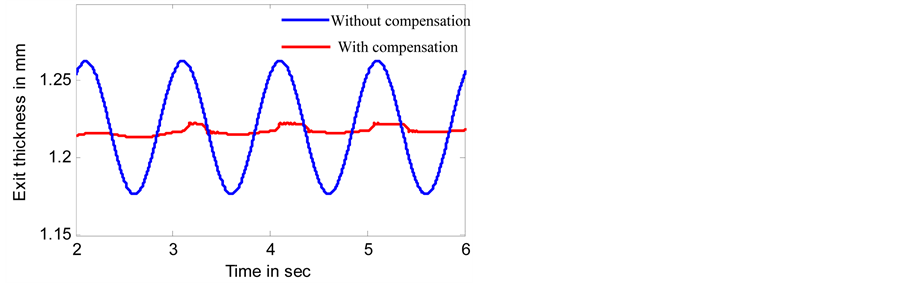
Figure 12. Exit thickness with and without compensation.
results, It is found that FNN is robust in that it eliminate the periodic thickness deviation considerably.
7. Conclusion
In this paper, the mathematical model of single-stand cold rolling mill is developed and PI controller has been used to control exit thickness of the strip. We propose FNN in order to reduce the effect of roll eccentricity. The error between the reference exit thickness and output thickness of stand is used as trajectory to adapt the primes part and the consequence part of the FNN so that the error goes toward zero. The output of FNN is added to the desired position roll gap to reduce periodic deviation in the output thickness. As we have shown in the simulation results, the performance of proposed method is good.
REFERENCES
- G. Zheng and Q.-Q. Qu, “Research on Periodical Fluctuations Identification and Compensation Control Method for Export Thickness in Rolling Mill,” IEEE Proceedings of the Eighth International Conference on Machine Learning and Cybernetics, Baoding, 12-15 July 2009, pp. 1972-1977.
- K. M. Takami, J. Mahmoudi and E. Dahlquist, “Adaptive Control of Cold Rolling System in Electrical Strips Production System with Online-Offline Predictors,” Springer International Journal of Advanced Manufacturing Technology, Vol. 50, No. 9, 2010, pp. 917-930. http://dx.doi.org/10.1007/s00170-010-2585-7
- G. Hwang, H.-S. Ahn, D.-H. Kim, T.-W. Yoon, S.-R. Oh and K.-B. Kim, “Design of a Robust Thickness Controller for a Single-Stand Cold Rolling Mill,” IEEE Proceedings of the International Conference on Control Applications, Dearborn, 15-18 September 1996, pp. 468-473.
- Mishra, et al., “Design of Hybrid Fuzzy Neural Network for Function Approximation,” Journal of Intelligent Learning Systems and Applications, Vol. 2, No. 2, 2010, pp. 97-109. http://dx.doi.org/10.4236/jilsa.2010.22013
- K. Naga Sujatha and K. Vaisakh, “Implementation of Adaptive Neuro Fuzzy Inference System in Speed Control of Induction Motor Drives,” Journal of Intelligent Learning Systems and Applications, Vol. 2, No. 2, 2010, pp. 110-118. http://dx.doi.org/10.4236/jilsa.2010.22014
- J. Pittner and M. A. Simaan, “Tandem Cold Metal Rolling Mill Control Using Practical Advanced Methods,” Springer-Verlag, New York, 2011. http://dx.doi.org/10.1007/978-0-85729-067-0
- Mikell P. Groover, “Fundamental of Modern Manufacturing,” John Wiley & Sons, Hoboken, 2007.
- M. Kutz, “Mechanical Engineers’ Handbook Manufacturingand Management,” John Wiley & Sons, Hoboken, 2006.
- B. Xu and P. Qian “Application of Adaptive Strategy Based on Model Prediction for the Stripe Thickness in Cold Rolling,” IEEE International Conference on Mechanic Automation and Control Engineering, 2010, pp. 3278-3281.
- S.-B. Tan and J.-C. Liu, “Research on Mill Modulus Control of Strip Rolling AGC Systems,” IEEE International Conference on Control and Automation, Guang zhou, May 30-June 1 2007, pp. 497-500.
- A. Kugi, W. Haas, K. Schlacher, K.Aistleitner, H. M. Frank and G. W. Rigler, “Active Compensation of Roll Eccentricity in Rolling Mills,” IEEE Transactions on Industry Applications, Vol. 36, No. 2, 2000, pp. 625-632. http://dx.doi.org/10.1109/28.833781
- J. Pittner and M. A. Simaan, “An Optimal Control Method for Improvement in Tandem Cold Metal Rolling,” IEEE Transactions on Industry Applications Annual Meeting, 2007, pp. 382-389.
- C.-T. Li and C. S. G. Lee, “Neural Fuzzy Systems: A Neuro-Fuzzy Synergism to Intelligen,” Prentice-Hall, New Jersey, 1996.
- A. Abraham, “Adaptation of Fuzzy Inference System Using Neural Learning,” Springer-Verlag, Berlin, Heidelberg, 2005.
- M. S. Mostafa, M. A. El-Bardini, S. M. Sharaf and M. M. Sharaf, “Fuzzy Neural Networks for Identification and Control of DC Drive Systems,” IEEE International Conference on Control Applications, Vol. 1, 2004, pp. 598- 603.
- A. ThamerRadhi, “Power System Protection Using Fuzzy Neural Petri Net,” Ph.D. Thesis, Basrah University, Iraq, 2012.
- S. A. H. A. Kareem, “Fuzzy Neural and Fuzzy Neural Petri Nets Control for Robot Arm,” MSc. Thesis, Basrah University, Iraq, 2010.
- Y. I. Al-Mashhadany, “Modeling and Simulation of Adaptive Neuro-Fuzzy Controller for Chopper-Fed DC Motor Drive,” IEEE Applied Power Electronics Colloquium (IAPEC), 2011, pp. 110-115.
- M. Dong, C. Liu and G. Y. Li, “Robust Fault Diagnosis Based on Nonlinear Model of Hydraulic Gauge Control System on Rolling Mill,” IEEE Transactions on Control Systems Technology, Vol. 18, No. 2, 2010, pp. 510-515. http://dx.doi.org/10.1109/TCST.2009.2019750
- L. E. Zarate and F. R. Bittencout, “Representation and Control of the Cold Rolling Process through Artificial Neural Networks via Sensitivity Factors,” Elsevier Journal of Materials Processing Technology, 2007, pp. 344- 362.


