Engineering
Vol.5 No.5A(2013), Article ID:31809,6 pages DOI:10.4236/eng.2013.55A005
Pitfalls and Remedies in DEA Applications: How to Handle an Occurrence of Zero in Multipliers by Strong Complementary Slackness Conditions
1New Mexico Institute of Mining and Technology, Department of Management, Socorro, USA
2Central Research Institute of Electric Power Industry, Tokyo, Japan
Email: toshi@nmt.edu, mika@criepi.denken.or.jp
Copyright © 2013 Toshiyuki Sueyoshi, Mika Goto. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 12, 2013; revised March 13, 2013; accepted March 22, 2013
Keywords: DEA; Strong Complementary Slackness Conditions; Linear Programming
ABSTRACT
This study discusses a guideline on a proper use of Data Envelopment Analysis (DEA) that has been widely used for performance analysis in public and private sectors. The use of DEA is equipped with Strong Complementary Slackness Conditions (SCSCs) in this study, but an application of DEA/SCSCs depends upon its careful use, as summarized in the guideline. The guideline consists of the five suggestions. First, a data set used in the DEA applications should not have a ratio variable (e.g., financial ratios) in an input(s) and/or an output(s). Second, radial DEA models under variable and constant Returns to Scale (RTS) need a special treatment on zero in a data set. Third, the DEA evaluation needs to drop an outlier. Fourth, an imprecise number (e.g., 1/3) may suffer from a round-off error because DEA needs to specify it in a precise expression to operate a computer code. Finally, when a large input or output variable may dominate other variables in DEA computation, it is necessary to normalize the data set or simply to divide each observation by its average. Such a simple treatment produces more reliable DEA results than the one without any data adjustment. This study also discusses how to handle an occurrence of zero in DEA multipliers by applying SCSCs. The DEA/SCSCs can serve for a multiplier restriction approach without any prior information. Thus, the propesed DEA/SCSCs can provide more reliable results than a straight use of DEA.
1. Introduction
Data Envelopment Analysis (DEA) has been long serving as a methodology to evaluate the performance of organizations in business, economics and other areas. The applicability of DEA is not limited in research areas in social science, rather extending to engineering and natural science. The father of DEA is Professor William W. Cooper (University of Texas at Austin) who worked on DEA from the beginning to 2012. The survey research [1] summarized his contributions in DEA from an academic perspective of management science and operation research, dating back to a linkage between DEA and L1 regression developed in 18th century and [2] documented his conceptual and philosophical contributions in accounting and economics, based upon which he developed DEA as a methodology of “social accounting” and “social economics”.
In the history of DEA, many DEA researchers (e.g., [3-5]) discussed the importance of incorporating SCSCs (Strong Complementary Slackness Conditions) into DEA. For example, the research of [4] documented what SCSCs were and then proposed a use of the primal-dual interior-point method that incorporated them into DEA algorithm. Acknowledging the importance of the interiorpoint method in solving DEA equipped with SCSCs, studies [6-8] have recently proposed a new use of SCSCs for DEA (hereafter, DEA/SCSCs) in primal-dual combined radial and non-radial models, so not the algorithmic perspective. Their original studies [6,7] applied DEA/ SCSCs for identifying a supporting hyperplane(s) on an efficiency frontier. Then, they determined the type and magnitude of RTS (Returns to Scale) based upon the upper and lower bounds of an intercept of a supporting hyperplane(s).
Acknowledging the contributions of many previous research efforts on DEA, this study recently finds that students, professors and individuals who are not familiar with DEA, attempt to use the methodology for their applications in which data sets have unexpected conditions. For example, a data set contains zero or negative. Another example is a data set that contains a ratio variable in an input(s) and/or an output(s). Furthermore, a data set whose observation has an outlier(s) and/or an imprecise number (i.e., 2/3) where 2/3 is mathematically precise, but the number becomes imprecise in operating a computer code. In these cases, DEA applications need to consider a special treatment for each case.
Besides such fundamental issues, this study discusses another problem, or an occurrence of zero in multipliers. This study knows that [9] first discussed the problem of zero in multipliers. To overcome the problem of zero in multipliers, DEA researchers have long discussed multiplier restriction methods such as assurance region analysis [10] and cone ratio [11]. Such approaches for multiplier restriction are very important in obtaining reliable results and related business/policy implications. However, the proposed approaches always need prior information (e.g., previous experience and scientific evidence). In many DEA applications, it is not easy for us to access such prior information. Moreover, the information contains a subjective decision by a user(s). The proposed use of SCSCs can omit the subjectivity in DEA assessment. No previous study has described such a use of SCSCs for multiplier restriction in DEA.
The remainder of this study is organized as follows: Section 2 provides an overview on an appropriate use of DEA. Section 3 describes mathematical formulations on DEA/SCSCs. Section 4 describes computational comments on DEA/SCSCs. Section 5 concludes this study along with future research directions of DEA.
2. Problems in DEA Applications
This section reviews a use of DEA and its fundamentals before describing DEA/SCSCs for multiplier restriction. The following concerns are important in applying DEA to various performance assessments. The violation needs a special treatment, depending upon each case and these combinations.
(a) Ratio Variable: A data set used in DEA applications should not have a ratio variable in an input(s) and/ or an output(s). To deal with the ratio variable, we need a series of modified DEA models. This study does not discuss the problem because [12] has provided a detailed description on the computational modification regarding DEA. A straightforward use of DEA does not properly function on the ratio variables. This concern is important because the original DEA model (i.e., CCR) has the mathematical structure of total weighted outputs divided by total weighted inputs. Thus, the structure of DEA has a ratio structure between inputs and outputs, so that these variables should not be ratio variables. In a similar manner, the proposed approach, or DEA/SCSCs, does not properly function on ratio variables, as well. This indicates that DEA/SCSCs need to develop a new approach to handle the ratio variable in an input(s) and/or an output(s). A future extension of DEA/SCSCs will explore the research task in another article.
(b) Zero or Negative in Data: Radial DEA models (i.e., CCR and BCC) need to treat zero in a data set, specially. As mentioned previously, [9] discussed about the special treatment in which a user needs to add a small number to zero. The treatment is practically acceptable, but mathematically problematic in DEA assessment, because the radial models produce different efficiency scores between with and without the treatment. Meanwhile, [8] has discussed a mathematical rationale regarding why the radial models cannot directly handle the occurrence of zero in a data set. According to [8], the radial models do not have the property of translation invariance so that they cannot directly handle an occurrence of zero in a data set. The property implies that an efficiency measure should not be influenced even if inputs and/or outputs shift toward a same direction by adding or subtracting a specific real number. Their study (in Table 1) indicates that RAM (Range-Adjusted Measure) has the property of “translation invariance” so that the non-radial model can handle an occurrence of zero in a data set. The property of the translation invariance is applicable to a negative value in data if a user depends upon the RAM. In contrast, it is impossible to apply radial models (i.e., BCC or CCR) and their related DEA/SCSCs to analyze a data set that contains zero or negative value in data.
(c) Outlier in Data: If an outlier exists in a data set examined by DEA, it is necessary to drop it from the data set because the outlier destroys the shape of an efficiency frontier so that DEA evaluation does not produce a reliable result. See, for example, [13] discussed how to handle the outlier issue in DEA.
(d) Imprecise Number: For example, an imprecise number (e.g., 1/3) may suffer from a round-off error because we need to specify the number by a precise expression to run a computer code. The number is mathematically acceptable, but not acceptable in the operation of a computer code for DEA. Some DEA investigator uses 0.3333 or the other may use 0.3334. To avoid the round-
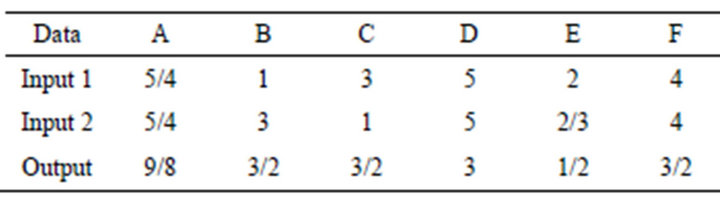
Table 1. An example.
off error, it is necessary to specify a data range between 0.3333 and 0.3334 in the example of 1/3. It is trivial that DEA may produce different solutions by depending upon the two round-off numbers. See, for example, [14] for a detailed description on how to handle such imprecise data in DEA. Thus, we need to depend upon a special treatment on the data set in DEA and DEA/SCSCs computations.
(e) Data Adjustment: When a large input or output variable dominates the other variables in terms of the magnitude, the large variable dominates the computation of DEA and DEA/SCSCs. In the case, it is necessary for users to normalize the data set or simply to divide each observation by its average. Such a simple data adjustment produces more reliable DEA results than the one without any data adjustment.
It is trivial to us that the problems discussed above originate from DEA itself, not SCSCs. The use of SCSCs depends upon only data sets that DEA can properly function. Otherwise, DEA/SCSCs may produce unacceptable results (e.g., a negative efficiency score, an unbounded solution, and an infeasible solution).
Finally, it is important to add that the use of DEA faces an occurrence of zero, but not a negative value, in data. However, when we apply DEA to a financial data set, the data usually contains financial ratios with negative variables. In the case, we need to depend upon a use of DEADiscriminant Analysis (DEA-DA) that has a special structure for analyzing various financial data sets, containing negative ratio variables. See, for instance, [15] for a description on DEA-DA and its related applications on financial performance assessments.
3. DEA/SCSCs
This study starts with reviewing a radial DEA model and then extends it to SCSCs. The model used in this section is a radial model (or so-called BCC: Banker-ChanersCooper) that is formulated under variable RTS. The DEA model has the following mathematical (input-based) structure to measure an efficiency score 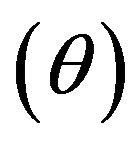 of the k-th DMU (Decision Making Unit,
of the k-th DMU (Decision Making Unit,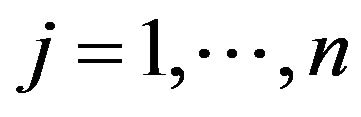 ) which uses an input vector
) which uses an input vector 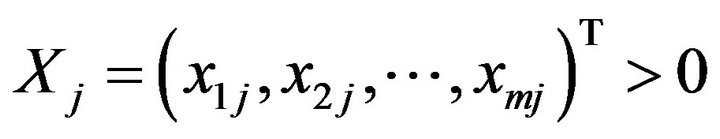 to produce an output vector
to produce an output vector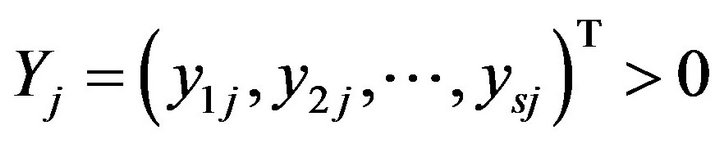 . The symbol
. The symbol
(T) indicates a vector transpose. It is important to note that a data set used for DEA performance evaluation should not violate the conditions summarized in Section 2.
The important feature of DEA is that it relatively determines the level of efficiency on the k-th DMU by comparing it with the other DMUs in terms of their multiple inputs and outputs. The following radial model may express the mathematical structure of DEA to measure the efficiency score of the k-th DMU:
 (1)
(1)
Here, the subscript 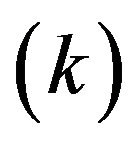 indicates the specific k-th DMU examined by Model (1). The scalar
indicates the specific k-th DMU examined by Model (1). The scalar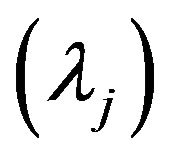 , often referred to as a “structural” or “intensity” variable, is used to make an analytical linkage among all DMUs in a data space. An efficiency score
, often referred to as a “structural” or “intensity” variable, is used to make an analytical linkage among all DMUs in a data space. An efficiency score 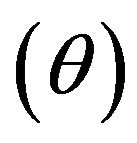 is unrestricted (URS) and it is often referred to as “technical efficiency” of the k-th DMU.
is unrestricted (URS) and it is often referred to as “technical efficiency” of the k-th DMU.
After incorporating slacks into Model (1), the formulation becomes as follows:
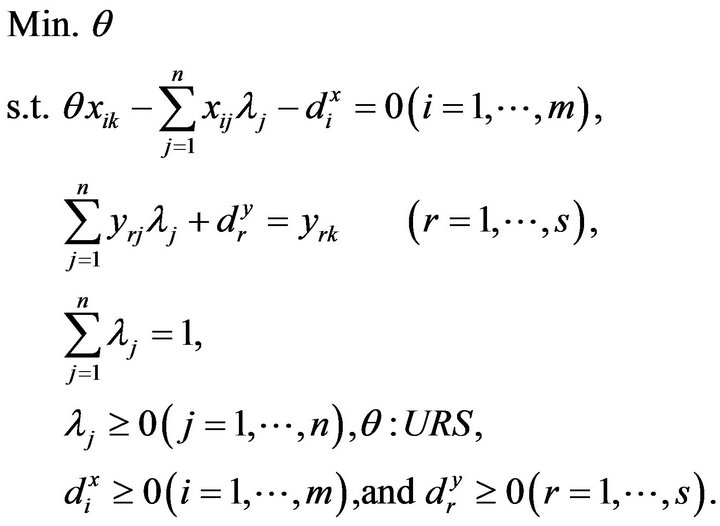 (2)
(2)
Here, 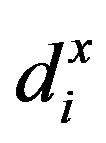 stands for the i-th input slack and
stands for the i-th input slack and 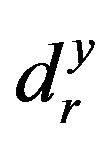 stands for the r-th output slack. Models (1) and (2) are mathematically same each other. However, there are two differences between them. One of the two differences is that Model (1) may consider the slacks (
stands for the r-th output slack. Models (1) and (2) are mathematically same each other. However, there are two differences between them. One of the two differences is that Model (1) may consider the slacks (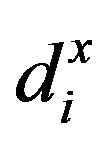 and
and ) as slack or surplus variables, but Model (2) considers them as decision variables in their computations. As a result, Model (2) can incorporate SCSCs more restrictively than Model (1). The other difference is that dual variables can be expressed by non-negative in Model (1) but they are unrestrictive (so, positive, zero and negative) in Model (2).
) as slack or surplus variables, but Model (2) considers them as decision variables in their computations. As a result, Model (2) can incorporate SCSCs more restrictively than Model (1). The other difference is that dual variables can be expressed by non-negative in Model (1) but they are unrestrictive (so, positive, zero and negative) in Model (2).
In addition to the two concerns, it is important to mention that the original radial formulation (e.g. BCC) maintains slack variables in the objective function so that it becomes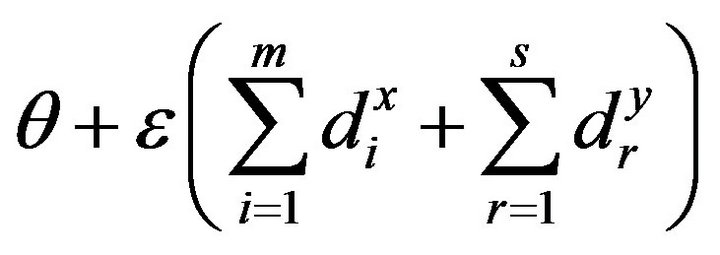 . An importance of the objective function is that the dual variables become always larger than or equal
. An importance of the objective function is that the dual variables become always larger than or equal![]() , so being always positive. In other words, a problem associated with Models (1) and (2) discussed in this study is that they may produce zero in their dual variables.
, so being always positive. In other words, a problem associated with Models (1) and (2) discussed in this study is that they may produce zero in their dual variables.
To describe the dual issue discussed above, this study returns to Model (1) and formulate its dual model in the following mathematical structure:
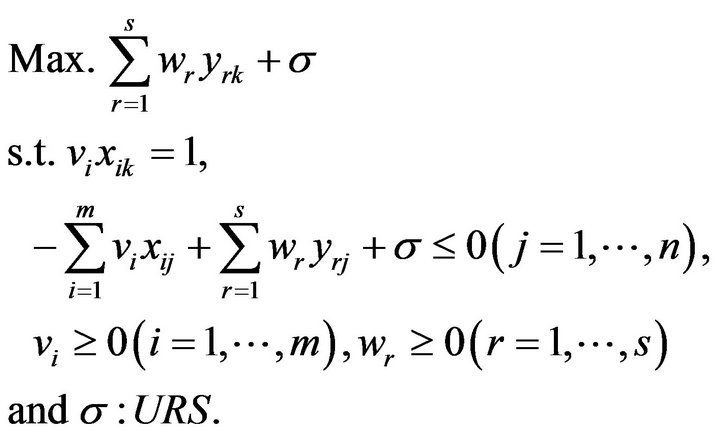 (3)
(3)
Here, 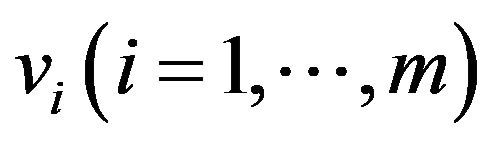 are the i-th dual variable related to the first set of constraints in Model (1) and
are the i-th dual variable related to the first set of constraints in Model (1) and 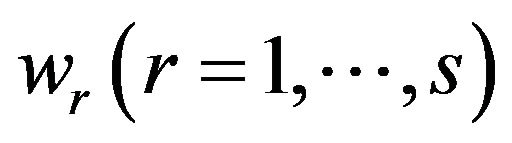 are the r-th dual variable related to the second set of constraints in Model (1), respectively. A dual variable
are the r-th dual variable related to the second set of constraints in Model (1), respectively. A dual variable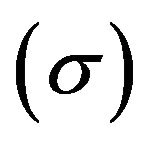 , being unrestricted (URS), is derived from the third constraint of Model (1). DEA researchers conventionally refer to each dual variable as a “multiplier”.
, being unrestricted (URS), is derived from the third constraint of Model (1). DEA researchers conventionally refer to each dual variable as a “multiplier”.
In the dual formulation of Model (2), all dual variables become unrestricted. To maintain the consistency between Models (1) and (2) in their dual formulations, this study incorporates the non-negativity on dual variables of Model (2), as formulated in Model (3).
SCSCs (Strong Complementary Slackness Conditions): The following Complementary Slackness Conditions (CSCs) exists between every optimal solution
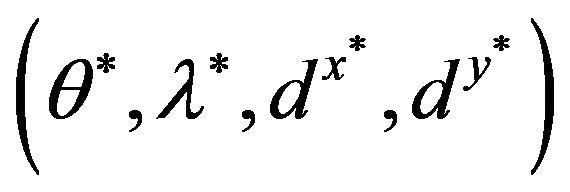 of Model (1) and every optimal solution
of Model (1) and every optimal solution 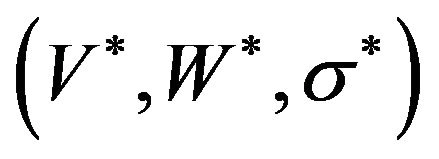 of Model (2):
of Model (2):
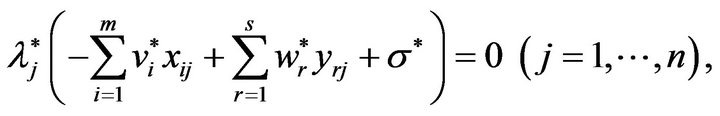 (4)
(4)
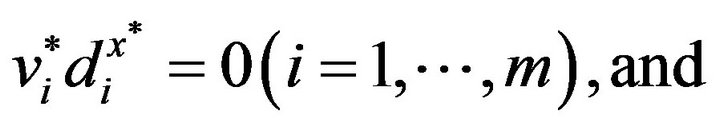 (5)
(5)
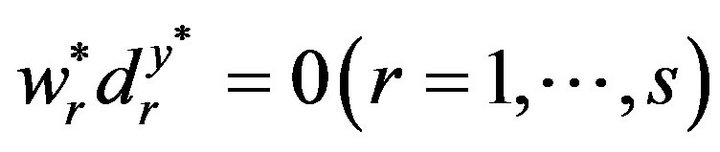 (6)
(6)
A pair of an optimal solution 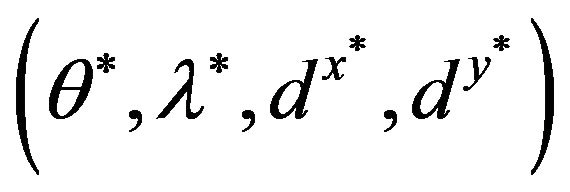 of Model (1) and an optimal solution
of Model (1) and an optimal solution 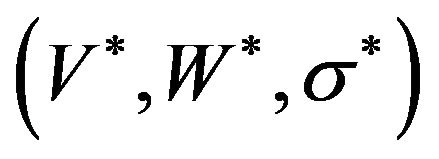 of Model (3) satisfies the following conditions:
of Model (3) satisfies the following conditions:
 (7)
(7)
 (8)
(8)
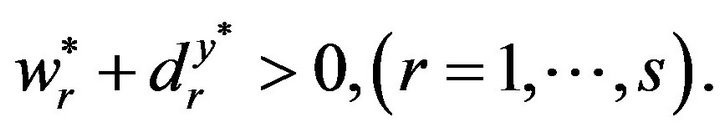 (9)
(9)
It is important to note that Model (3) has
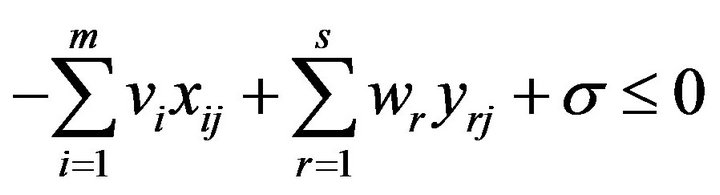
or

Therefore, this study incorporates
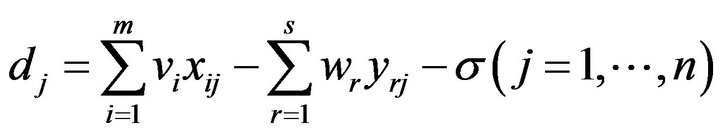
in Equation (7) in such a manner that
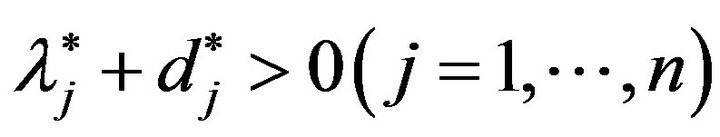 .
.
The satisfaction from Equations (7) to (9) is referred to as “Strong CSCs”, or SCSCs. See [7] for a discussion on SCSCs.
DEA/SCSCs between Models (1) and (3) combine all constraints in Models (1) and (3) along with SCSCs:
 (10)
(10)
where the equation 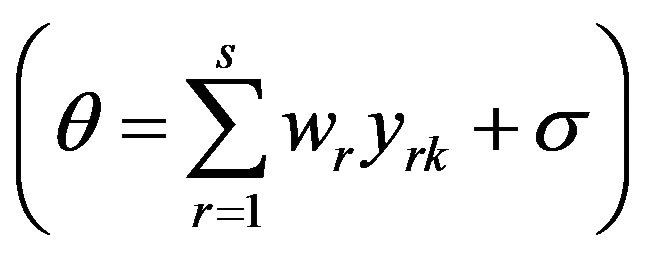 indicates that the objective of Model (1) is equivalent to that of Model (3). The last group of constraints indicates that an optimal solution obtained from Model (10) can satisfy SCSCs (7-9). An unknown decision variable
indicates that the objective of Model (1) is equivalent to that of Model (3). The last group of constraints indicates that an optimal solution obtained from Model (10) can satisfy SCSCs (7-9). An unknown decision variable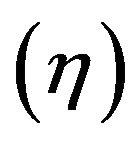 is incurporated into Model (10) in order to maintain SCSCs on optimality.
is incurporated into Model (10) in order to maintain SCSCs on optimality.
It is possible to replace Model (1) with Model (2) in Model (10) to incorporate the influence of slacks more clearly. Mathematically, the two models do not have any difference except the sign of dual variables. However, they are computationally different, as mentioned previously. Furthermore, the multiplier restriction by SCSCs functions on efficient DMUs, not inefficient DMUs. However, it is true that only efficient DMUs consist of an efficient frontier, based upon which DEA evaluates the performance of all DMUs.
4. Comments on Computation
The number of constraints determines the computational time of DEA because it determines the size of a basic matrix in linear programming. It is true that DEA/SCSCs has longer side constraints than original DEA. For example, the number of constraints in Model (1) has 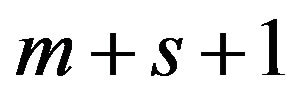 and that of Model (10) has
and that of Model (10) has 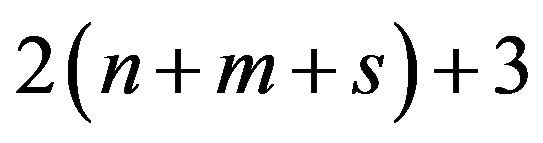 where n is usually larger than
where n is usually larger than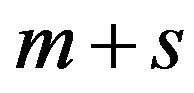 . The size of a basic matrix of DEA/SCSCs becomes much larger than that of DEA. In the case, as discussed in [16], a column reduction technique of linear programming becomes useful in the computation after changing Model (10) to a dual formulation. See, for example, [17,18] for a detailed discussion on DEA special algorithms.
. The size of a basic matrix of DEA/SCSCs becomes much larger than that of DEA. In the case, as discussed in [16], a column reduction technique of linear programming becomes useful in the computation after changing Model (10) to a dual formulation. See, for example, [17,18] for a detailed discussion on DEA special algorithms.
To overcome the computational problem of DEA/SCSCs, this study proposes two possible approaches. One of the two approaches is a use of the primal-dual interiorpoint method, proposed by [4], because the method can simultaneously solve the primal part and the dual part of Model (10) so that the computation time of Model (10) is almost same as that of Model (1). Second-Order Cone Programming (SOCP) is the most promising approach among primal-dual interior methods. See [19] for a description on how to use SOCP for DEA.
The other approach is that we can utilize network computing, proposed by [16], which connects multiple computers and synchronizes them as a single computing entity for DEA. See a large simulation study of the network computing in their study. If we apply the network computing to Model (10) and ordinal linear programming software to Model (1), then the former computational time is much faster than the latter. Thus, DEA/SCSCs has many computational options in dealing with a large data set (e.g., more than 100,000 DMUs). The combination between primal-dual interior point method (e.g., SOCP) and network computing equipped with column reduction technique can very effectively solve various large DEA/ SCSCs.
Finally, it is not necessary for us to use special computer schemes, as discussed above, because a modern computer is very efficient and fast. The computer developments are much faster than algorithmic developments in recent days. Thus, the computation of DEA/SCSCs can depend upon the modern computer in dealing with a small data set (e.g., less than 1,000 DMUs).
5. Conclusion and Future Extensions
This study provided a set of guidelines for a proper use of DEA and DEA/SCSCs. The DEA/SCSCs is mathematically correct, but its successful applications of SCSCs depend upon a careful use, as summarized in this study. All the guidelines discussed for DEA/SCSCs are applicable to a proper use of DEA, as well. Besides the guidelines, this study discussed implications of SCSCs from the primal and dual aspects of DEA/SCSCs. Such two aspects on SCSCs have been never explored in the previous DEA studies.
It is true that both DEA and DEA/SCSCs are not perfect. There are many problems associated with their uses in addition to the problems discussed in this study. For example, DEA assumes that all DMUs use same inputs and same outputs. The underlying assumption is often unrealistic in modern business. For example, a firm uses three inputs to produce two outputs. Meanwhile, another firm uses four inputs to three outputs. Thus, different firms use different combinations between inputs and outputs. The number of inputs and outputs are usually different among firms. In the case, it is impossible for us to apply DEA under such a business environment. That is a major problem associated with DEA, so becoming an important future research task for this study.
It is also true that managers of each firm have their own learning capabilities to adjust their strategic behaviors in a dynamic time horizon. The previous studies did not pay attention to the learning capabilities of managers. The observation on business reality suggests that DEA research needs to direct itself toward a combination between DEA and artificial intelligence (e.g., agent-based approach for complex analysis) in computer science. It can be easily envisioned that such a combined research effort will open up a new research area for DEA.
In conclusion, it is hoped that this study contributes in DEA. We look forward to seeing future research extensions, as suggested in this study.
REFERENCES
- F. Glover and T. Sueyoshi, “Contributions of Professor William W. Cooper in Operations Research and Management Science,” European Journal of Operational Research, Vol. 197, No. 1, 2009, pp. 1-16. doi:10.1016/j.ejor.2008.08.011
- Y. Ijiri and T. Sueyoshi, “Revisiting Accounting Essays by William W. Cooper: In Commemorating His 95th Birthday,” ABACUS: A Journal of Accounting, Finance and Business Studies, Vol. 46, No. 4, 2010, pp. 464-505.
- A. Charnes, W. W. Cooper and R. M. Thrall, “A Structure for Classifying and Charactering Efficiency and Inefficiency in Data Envelopment Analysis,” Journal of Productivity Analysis, Vol. 2, No. 2, 1991, pp. 197-237. doi:10.1007/BF00159732
- M. D. Gonzalez-Lima, R. A. Tapia and R. M. Thrall, “On the Construction of Strong Complementarity Slackness Solutions for DEA Linear Programming Problems Using a Primal-Dual Interior-point Method,” Annals of Operations Research, Vol. 66, No. 1, 1996, pp. 139-162. doi:10.1007/BF02187298
- W. W. Cooper, L. S. Seiford and K. Tone, “Introduction to Data Envelopment Analysis and Its Uses with DEASolver Software and References,” Springer, New York, 2006.
- T. Sueyoshi and K. Sekitani, “Measurement of Returns to Scale by a Non-Radial DEA Model: A Range-Adjusted Measure Model,” European Journal of Operational Research, Vol. 176, No. 3, 2007, pp. 1918-1946. doi:10.1016/j.ejor.2005.10.043
- T. Sueyoshi and K. Sekitani, “The Measurement of Returns to Scale under a Simultaneous Occurrence of Multiple Solutions in a Reference Set and a Supporting Hyperplane,” European Journal of Operational Research, Vol. 181, No. 2, 2007, pp. 549-570. doi:10.1016/j.ejor.2006.05.042
- T. Sueyoshi and K. Sekitani, “An Occurrence of Multiple Projections in DEA-Based Measurement of Technical Efficiency: Theoretical Comparison among DEA Models from Desirable Properties,” European Journal of Operational Research, Vol. 196, No. 2, 2009, pp. 764-794. doi:10.1016/j.ejor.2008.01.045
- R. G. Thompson, P. S. Dharmapala and R. M. Thrall, “Importance for DEA of Zero, Multipliers and Solutions,” Journal of Productivity Analysis, Vol. 4, No. 2, 1993, pp. 379-390. doi:10.1007/BF01073546
- R. G. Thompson, F. D. Singleton, R. M. Thrall and B. A. Smith, “Comparative Site Evaluation for Locating a HighEnergy Physics Lab in Texas,” Interface, Vol. 16, No. 6, 1986, pp. 35-49. doi:10.1287/inte.16.6.35
- A. Charnes, W. W. Cooper, Q. L. Wei and Z. M. Huang, “Cone Ratio Data Envelopment Analysis and Multi-Objective Programming,” International Journal of System Science, Vol. 20, No. 5, 1989, pp. 1099-1118. doi:10.1080/00207728908910197
- A. Emrouznejad and G. R. Amin, “DEA Models for a Ratio Data: Convexity Consideration,” Applied Mathematical Modelling, Vol. 33, No. 1, 2009, pp. 486-498. doi:10.1016/j.apm.2007.11.018
- N. A. Tran, G. Shively and P. Preckel, “A New Method for Detecting Outliers in Data Envelopment Analysis,” Applied Economics Letters, Vol. 15, No. 1, 2008, pp. 1-4.
- W. W. Cooper, K. S. Park and G. Yu, “IDEA and ARIDEA: Models for Dealing with Imprecise Data in DEA,” Management Science, Vol. 45, No. 4, 1999, pp. 597-607. doi:10.1287/mnsc.45.4.597
- T. Sueyoshi and M. Goto, “A Use of DEA-DA to Measure Importance of R&D Expenditure in Japanese Information Technology Industry,” Decision Support Systems, Vol. 54, No. 2, 2013, pp. 941-952. doi:10.1016/j.dss.2012.09.017
- T. Sueyoshi and T. Honda, “DEA Network Computing in Multi-Stage Parallel Processes,” International Transactions in Operational Research, Vol. 10, No. 3, 2003, pp. 217-244. doi:10.1111/1475-3995.00405
- T. Sueyoshi, “Algorithmic Strategy for Assurance Region Analysis in DEA,” Journal of the Operations Research Society of Japan, Vol. 35, No. 1, 1991, pp. 62-76.
- T. Sueyoshi, “Measuring Technical, Allocative and Overall Efficiencies Using DEA Algorithm,” Journal of the Operational Research Society, Vol. 43, No. 2, 1992, pp. 141-155.
- T. Sueyoshi and K. Sekitani, “Computational Strategy for Russell Measure in DEA: Second-Order Cone Programming,” European Journal of Operational Research, Vol. 180, No. 1, 2007, pp. 459-471. doi:10.1016/j.ejor.2006.02.042

