Engineering
Vol.4 No.12(2012), Article ID:25854,4 pages DOI:10.4236/eng.2012.412110
Dynamic Characteristics Evaluation of Innovative UHPC Pedestrian Cable Stayed Bridge
Structural Engineering Research Division, Korea Institute of Construction Technology, Goyang, South Korea
Email: wjchin@kict.re.kr, yjkim@kict.re.kr, chojr@kict.re.kr, jSpark1@kict.re.kr
Received September 3, 2012; revised October 5, 2012; accepted October 17, 2012
Keywords: UHPC; Pedestrian Cable Stayed Bridge; Dynamic Characteristics Test; TMD
ABSTRACT
KICT (Korea Institute of Construction Technology) is conducting a project called “SUPER BRIDGE 200—Development of Low Cost and Long Life Hybrid Cable Stayed Bridge”. This project aims to reduce the construction and maintenance costs of long-span bridges by 20% and double their lifetime through the exploitation of ultra-high performance concrete (UHPC). This paper presents the design and construction of the first pedestrian cable stayed bridge using UHPC developed by KICT. UHPC, compared to conventional concrete, has not only high compressive and tensile strengths but also high ductility. The UHPC developed at KICT is a steel fiber-reinforced cement compound presenting design compressive strength larger than 180 MPa and design tensile strength exceeding 10 MPa with water-to-binder ratio below 0.24 and admixing of 2 volume percentage of steel fiber. To show the applicability of UHPC to structures, a pedestrian cable stayed bridge (Super Bridge I) exploiting the characteristics of the developed UHPC has been planned, designed and erected at KICT. The dimension of UHPC deck is 2.7 m × 7 m as a precast segment with a typical thickness of deck of only 7 cm. However, harmful crack was observed in the deck at the time of the fabrication of the deck segments. Accordingly, new fabrication method was conceived and applied to prevent cracking of the UHPC slender deck. Four UHPC deck segments were fabricated successfully without any crack. After construction, the dynamic characteristics (natural frequencies and mode shapes) were evaluated through vibration tests since several users felt excess vibration. A vertical tuned mass damper (TMD) was proposed and installed on the parapet of the bridge. The TMD reduces the acceleration by about 30% from 0.0316 g to 0.0244 g when two pedestrians are crossing the bridge.
1. Introduction
In order to overcome the drawbacks of conventional concretes, Ultra High Performance Concrete (UHPC) is a material presenting high strength as well as tensile strength and flexural strength that was developed to secure the ductility and strength of the structural members by improving significantly resistance to cracking, shear resistance and resistance to impact through the introduction of steel fibers and admixtures. Development started with Ductal® of Lafarge in France [1]. To date, there are a very few examples of application of UHPC to bridges. The first application of UHPC to bridge dates back to 1997 in with Sherbrooke Bridge, a pedestrian bridge in Canada. Thereafter, the first road bridge applying UHPC appeared in 2004 in Australia with Shepherds Bridge. Further applications are Papatoetoe Station Viaduct in New Zealand, Chabotte Bridge in France, and Sakata Mirai pedestrian bridge in Japan. Recently, UHPC was also applied to railway bridge with Kayokawa Bridge completed in 2010 in Japan indicating the gradual expansion of the application of UHPC. In Korea, Ductal® found its first application to the construction of a pedestrian bridge, Seonyu Bridge, in 2002. Currently, KICT (Korea Institute of Construction Technology) is undertaking the “SUPER BRIDGE 200—Development of Low Cost and Long Life Hybrid Cable Stayed Bridge” project. This project aims to reduce the construction and maintenance costs of longspan bridges by 20% and double their lifetime through the exploitation of UHPC. KICT developed the KICTUHPC, a fiber-reinforced cement composite providing design compressive strength larger than 180 MPa and design direct tensile strength larger than 10 MPa with a water-to-binder ratio below 0.24 and volume percentage of fiber larger than 2 vol.%. As part of this project, KICT implemented the construction of a pedestrian cable stayed bridge, Super Bridge I, applying UHPC for the first time in the world (Figure 1). Super Bridge I has been built as a pathway linking the main building of KICT and the third floor of a nearby newbuilt building. The pedestrian cable stayed bridge is composed of a unique pylon on which 3 series of fan type cables are attached in three directions. The precast girder uses KICT-UHPC with design com-

Figure 1. Super Bridge I, the UHPC cable stayed bridge at KICT.
pressive strength of 180 MPa. The adoption of UHPC made it possible to realize a slim cross-section for the girder. The impossibility to install a bearing supporting the girder in the existing building constrained us to apply a cantilever structure for the girder [2]. This implies that the structure exhibits characteristics very vulnerable to vibration under the passage of pedestrians. Therefore, vibration test was conducted to measure the natural frequencies as well as the vibrational acceleration and displacement of the bridge, and to evaluate its dynamic characteristics. The results revealed the occurrence of excessive vertical vibrations that necessitate the design and installation of a vibration control device in order to improve the serviceability of the bridge and comfort of the users. This paper presents the characteristics of the developed KICT-UHPC and the construction process of a pedestrian bridge exploiting this material. The design, fabrication, installation and verification of the tuned mass damper (TMD) installed as vibration control device are also described.
2. Characteristics of KICT-UHPC
Since 2002, KICT started the development of UHPC targeting a characteristic strength of 200 MPa (design compressive strength of 180 MPa). In the present stage, KICT-UHPC exhibits remarkable ductile behavior and fracture energy absorption performance (Table 1), and is also securing a lifespan of 200 years. The developed material is a fiber-reinforced cement composite providing design compressive strength larger than 180 MPa (Figure 2) and design direct tensile strength larger than 10 MPa (Figure 3) with a water-to-binder ratio below 0.24 and volume percentage of fiber larger than 2 vol.% [3].
3. Design of the UHPC Pedestrian Cable Stayed Bridge, Super Bridge I
3.1. Summary
There is no specific design code for UHPC in Korea to date. In foreign countries, proposals of design specifica-
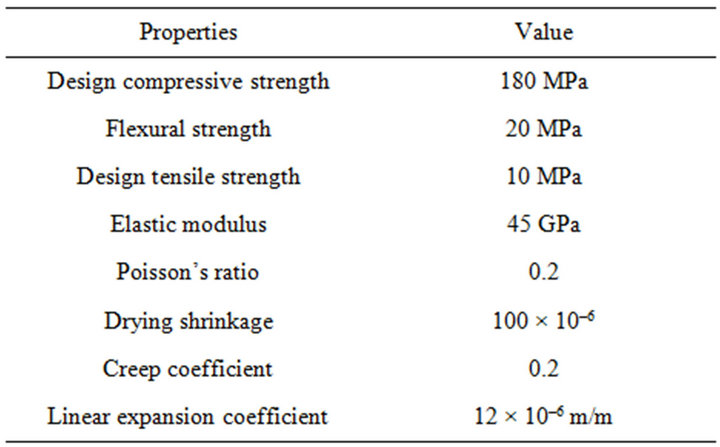
Table 1. Mechanical properties of KICT-UHPC (vf = 2%).
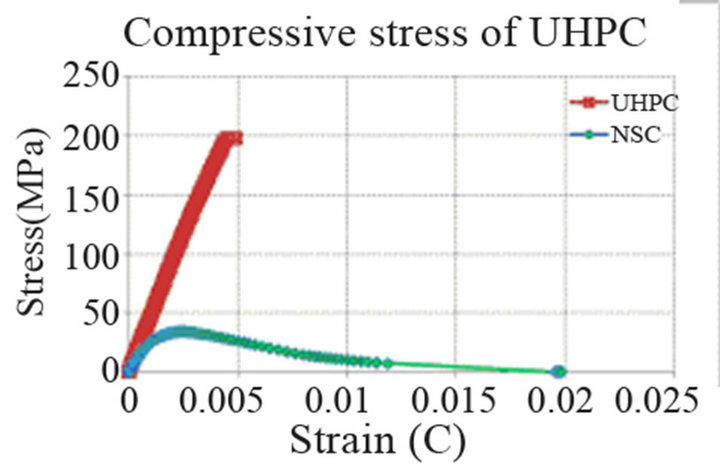

Figure 2. Compressive strength test of KICT-UHPC.
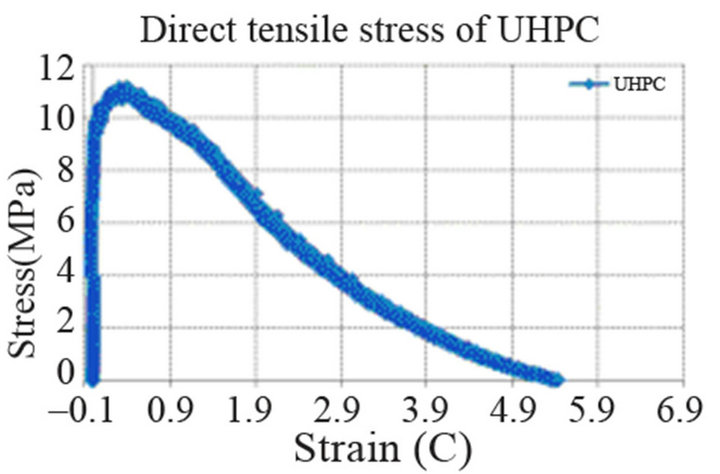

Figure 3. Direct tensile strength test of KICT-UHPC.
tions have been established but most of the specifications must be computed based on tests. For the design of UHPC cable stayed bridge, proposal of UHPC Standards and Structure Design Code based on the experimental studies performed in this project were applied and reference was done to foreign experimental research documents and proposals of UHPC design codes. Common features were dealt by applying the Korean Highway Bridge Design Code and Design Code for Concrete Structures. The following gives a list of the design codes and guidelines referred in this study [4,5].
- Proposal of UHPC Standards and Structure Design Code (KICT, 2009);
- Proposal of Guidelines for the Design and Construction of UHPC Fiber-Reinforced Concrete (JSCE, 2004);
- Ultra High Performance Fiber-Reinforced Concrete (SETRA-AFGC, 2002);
- Ductal Design Rules (LAFARGE, 2000);
- Highway Bridge Design Code (Ministry of Land, Transportation and Maritime Affairs, 2005);
- Design Code for Concrete Structures (Ministry of Land, Transportation and Maritime Affairs, 2003);
- Manual for the Design, Construction and Maintenance of Facilities (Pedestrian Bridges) (Seoul Metropolitan Government, 2001);
- Design Guidelines for Cable-Supported Steel Bridges (KSCE, 2006);
- AASHTO LRFD Bridge Design Specification (USA, 2004);
- PTI Recommendation for Stay Cable Design (USA, 2001).
3.2. Design Loads and Load Combination
The dead load of KICT-UHPC is 25.5 kN/m3 and the design live loads are as follows (Table 2).
As a special bridge applying stay cables, the adopted load combinations for the pedestrian bridge correspond to those of the Highway Bridge Design Code (2005), the Design Guidelines for Cable-Supported Steel Bridges (2006) and the Recommendations for Stay Cable Design (PTI, 2001). The combination relative to the replacement and breakage of cable complies with the Design Guidelines for Cable-Supported Steel Bridges (2006) for the allowable stress design method and the Recommendations for Stay Cable Design (2001) for the strength design method.
3.3. Design of Upper Girder
The common part of the girder was planned a precast girder using UHPC with design compressive strength of 180 MPa. Based on test results, a value of 0.4fck (72 MPa) was applied for the allowable compressive stress of KICT-UHPC. A value of 8 MPa was applied for the allowable tensile stress but was assumed to be zero at the connections. Edge girder was selected as cross-section of the girder to exploit at the most the compressive strength of UHPC (Figure 4). The deck was design with a thickness of about 70 mm to be very slim. The precast segments were planned to be fabricated by match cast. The connection was designed by pretensioning 7 steel strands (diameter = 12.7 mm, fpu = 1900 MPa) up to 0.75fpu disposed in the edge girder after application of epoxy, followed by the tensioning the Φ26 mm steel bars (fpu =1230 MPa) installed in the deck up to 0.7fpu. Considering the connection with the pylon, the portions contiguous to the pylon were designed to be cast-in-place concrete. The cables are Φ20.2 mm OSS (Pferifer) with tensile strength (fsu) of 1670 MPa and elastic modulus (Es) of 150 GPa. An allowable tensile stress of 0.45fsu was
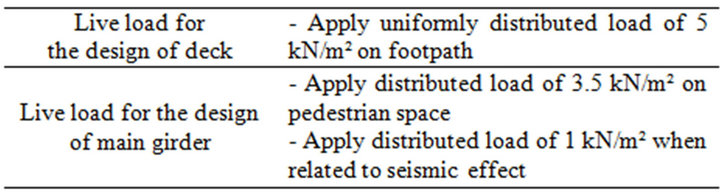
Table 2. Design live load.
applied (Figure 5).
4. Construction of the UHPC Pedestrian Cable Stayed Bridge, Super Bridge I
4.1. Fabrication of Precast Segments
KICT-UHPC is characterized by self-compacting properties with slump flow larger than 230 mm which render it unnecessary to conduct vibration compaction. Moreover, if placing is done in two steps with a definite interval between the two steps, the absence of steel fibers oriented vertically to the construction joint arises as a problem. However, a difference of level exists between the edge girder and deck in the precast segment. In order to avoid the problem of construction joint at the step connection, a steel cover was fabricated and placing of KICT-UHPC was conducted at once without time interval. The placing process started first at the center of the deck. Thereafter, the cover was installed and the part of the edge girder with the step was placed at the end of the process. Shrinkage reducing agent and expansion agent were admixed additionally at rate of 1% and 7.5%, respectively, on the side of the material to prevent cracking of the deck (Table 2). For the fabricated sides, shrinkage absorbing material (Styrofoam) with thickness of 5 mm was installed on the inner face inside the girder to prevent the effect
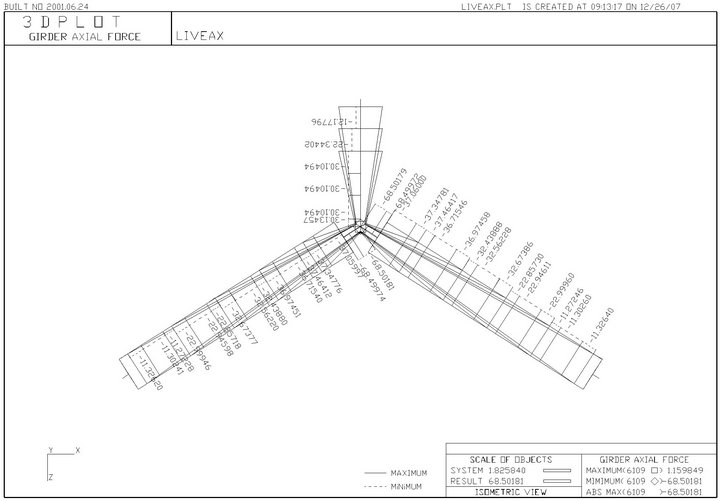
Figure 4. Structural analysis model and analysis results.
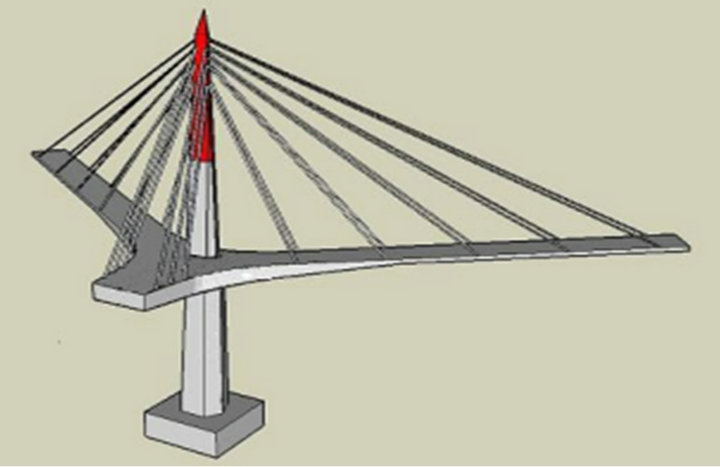
Figure 5. Drawing of the pedestrian bridge.
of autogenous shrinkage of UHPC, and a PE film was disposed on the bottom of the deck to reduce friction. Table 3 summarizes the mix proportions of KICT-UHPC. A pan type mixer with capacity of 1.5 m3 appropriate for the mixing of UHPC was used. Mixing proceeded first by dry mix of the mix composed of type 1 Portland cement, silica fume, filler and aggregates. After sufficient mixing, water, superplasticizer and admixtures were introduced and mixing continued until securing of the prescribed slump flow. Finally, the mix composition was completed by introducing 2 vol% steel fibers (φ0.2 – 13 mm) Placing of KICT-UHPC was conducted over the form using a hopper. Since UHPC contains relatively large quantities of silica fume, its initial hardening starts late. Therefore, the segments were moved to their curing site after having secured sufficient stiffness for their lifting and transport by conducting dry curing during 48 hours. Thereafter, steam curing was carried out during 48 hours at 90˚C. Since sudden elevation and drop of the temperature may generate thermal cracks in the segment, the upward and downward variations of temperature were executed gradually at a rate of 15˚C/h.
4.2. Erection
After erection of the pile foundation and installation of the steel pylon, a total of 4 precast segments were installed at a rate of 2 segments per one cantilevered girder (Figure 6). The precast segments were fastened by pretensioning the tendons in the edge girder and tensioning the steel bars of the deck. Thereafter, concrete was castin-placed at the connections with the pylon. After application of the secondary permanent loads such as the parapet, the tension of the cables was adjusted to secure the design camber of the upper girder [6].
5. Dynamic Characteristics of the UHPC Pedestrian Cable Stayed Bridge, Super Bridge I
5.1. Summary
Long-span structures exhibiting low natural frequency like the pedestrian bridge are prone to excessive vibrations caused by dynamic loading such as the pedestrian load applied by the users. Such vibrational phenomenon is not only provoking discomfort of the user but also raises problems of serviceability and safety due to excessive vibrations exceeding the limiting threshold of the bridge when the frequency of the pedestrians coincides with the natural frequency of the bridge. The UHPC pedestrian cable stayed bridge experimented in this study was constructed as a cantilevered structure following the impossibility to install bearings or anchoring systems in the existing buildings connected by the bridge. Such structural characteristics and the slim structure achieved through the application of UHPC render inevitably the bridge vulnerable to vibration. To confirm this fact, users complained of their discomfort and loss of convenience caused by the vibration of the pedestrian bridge and led to the consideration of vibration control. Comparative analysis of the dynamic behavior of the bridge was conducted through analytic and experimental methods to evaluate the vibrational serviceability of the bridge and establish a solution for vibration control [7].
5.2. Dynamic Characteristics under Pedestrian Loads
Pedestrian load is influenced by various factors including the weight of the pedestrian or his walking frequency, speed, walking form, and personal walking habit. Such

Table 3. Mix composition of KICT-UHPC.

Figure 6. Installation of UHPC deck.
load can be thus expressed by means of various load-time history models. In order to evaluate whether sufficiently large dynamic responses are generated by these pedestrian load models, free vibration analysis was conducted using the commercial program SAP2000 on the 3-dimensional model of the bridge. Frame elements were used for the edge girder, deck and pylon, and truss elements were adopted to provide simplified model of the cables.
The analysis results can be summarized as follows:
- Structural mass: 225.91 kN·sec2/m;
- 1st mode natural frequency: 2.05 Hz;
- 1st mode frequency: 0.49 sec;
- 1st mode mass participation ratio: 94.80 %;
- 1st modal mass: 214.16 kN·sec2/m.
The first natural frequency of 2.05 Hz predicted by the analysis results was very close to the frequency of the pedestrian load caused by users walking at regular step. Accordingly, high risk of resonance to occur for the pedestrian bridge could be forecast. Since the dynamic behavior of the actual pedestrian bridge depends on a larger set of factors including the tension of the cable, its real natural frequency may differ from the analytically obtained value. Therefore, test was performed to evaluate exactly the natural frequency and comparison with the analysis was done to evaluate the resonance frequency of the pedestrian cable stayed bridge. The natural frequency and maximum vibrational acceleration as well as the dynamic deflection at the end of the deck were measured through loading test (Figure 7). Being a pedestrian bridge, the natural frequency was estimated under loaded condition according to the walking and jumping of users. The testing method is described in Table 4. The natural frequency under running of two people was 1.91 Hz (Figure 8). Since the load frequency of a walking pedestrian runs around 2 Hz, it appeared that the installation of TMD was required to prevent resonance.
6. Solution for Vibration Control
6.1. Summary
The current UHPC cable stayed pedestrian bridge experienced excessive vertical vibrational accelerations larger than the limit value of 0.1 g (Manual for the De-
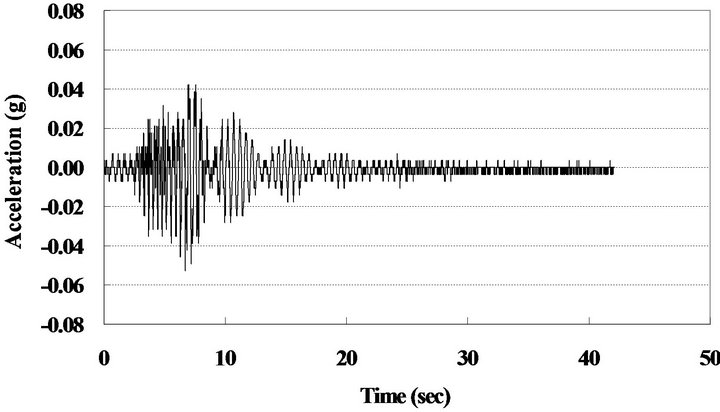
Figure 7. Acceleration response (2 pedestrians running).
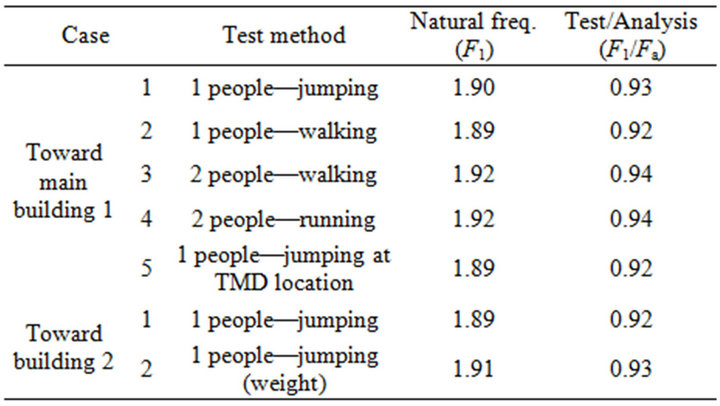
Table 4. Initial forced vibration test.
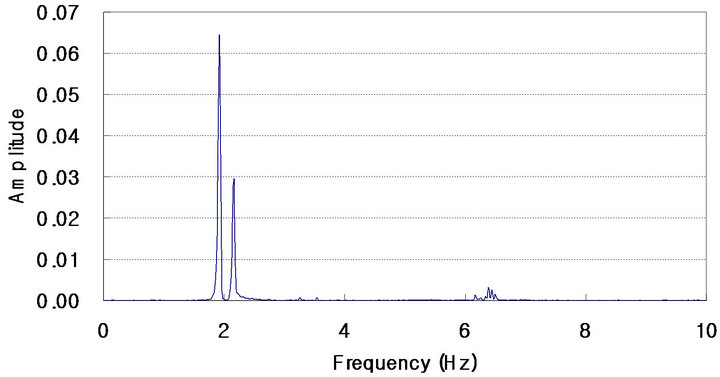
Figure 8. PSD (2 pedestrians running).
sign, Construction and Maintenance of Facilities). The measurement results of the initial forced vibration test revealed that the maximum vibrational acceleration reached about 0.11 g. Accordingly, Tuned Mass Dampers (TMDs) were installed on the parapet of the pedestrian bridge to improve its serviceability by reducing the vertical acceleration below 0.1 g. The installation process of the TMDs was conducted according to the following sequence.
1) Decision and fabrication of TMDs
- Design (dimensions) and fabrication conducted after 3-D structural analysis and initial forced vibration test
- Test of fabricated TMDs at factory;
- Selection of installation locations of TMDs;
2) Installation of TMDs on the pedestrian cable stayed bridge.
- A total of 4 units installed at a rate of 2 units per side at the parapet of the bridge.
3) Performance verification test.
6.2. Vertical Vibration Control Device (TMD)
TMD applies the principle of the dynamic vibration absorber traditionally applied in mechanical engineering to civil structures. This device absorbs the vibration of the bridge by tuning the natural frequencies of the bridge and device. The weight of the TMD is generally set to approximately 1% of that of the host structure. TMD as a passive vibration control device offers the advantages of not requiring separate supply of electric power and being semi-permanent. Examples of its application can be found among others in Millennium Bridge in London, UK, Bellagio Pedestrian Bridge in Las Vegas, Nevada USA, Yokohama Bay Bridge in Yokohama, Japan. The TMD for footbridge enhances the serviceability by reducing the vibration of the bridge through the efficient absorption of the energy transmitted by the external load (pedestrian load) to the bridge. TMD is a typical passive vibration control device, which exploits the inertial force and featured by the needlessness of electric power and stable behavior. TMS is essentially composed of masses, springs, damper, frame and various types of substructure. TMD should be installed at the location exhibiting the largest vibration in the host structure to develop maximum vibration control [8].
The movable mass of the TMD was computed to be 0.5% of the 1st modal effective mass.
- Movable mass of vibration reducing device: 214.16 × 0.005 = 1.0708 kN·sec2/m;
- 4 TMDs installed at a rate of 2 units at each end of the pedestrian bridge;
- Mass of each TMD: 1.0708/4 = 0.2677 kN·sec2/m;
- Movable mass of vertical TMD: 0.2677 × 9.806 = 263 kgf.
The design movable mass of TMD was determined to be 264 kgf per unit considering the workability of steel.
- Modified mass ratio (m) : m = 1.0708/214.16 = 0.005
- Frequency ratio of vertical TMD (fR):
fR = 1/(1 + μ) = 0.995;
- Optimal damping ratio of vertical TMD (zT): zT = 0.04 (Table 5 and Figure 9).
6.3. Analysis of Vibration Control Effect by Dynamic Loading Test
The forced vibration tests distinguished regular walking, fast walking, running and jumping considering 1, 2, 5 and 10 pedestrians so as to conduct the tests under diverse loading cases. By varying the speed, pace and load, each load case was performed twice and comparison was done of the measurements collected under operation and shut off of the TMDs. Walking tests were carried out at speeds of 2.16 km/h for regular walking, 5.4 km/h for fast walking, and 8.1 km/h for running while maintaining constant speed and spacing. Figures 10 and 11 illustrate the walking test and Figures 12-14 plot the dynamic responses.
Under operation of the TMDs, for Load Case 4 (2 people walking regularly), 2 people averaging a mass of 167 kg walked at slow speed of 2.16 km/h, i.e. pace of 60 cm/s, at spacing of 60 cm to each other through a course starting from the main building to the new building and returning to the main building. The corresponding maximum displacement and maximum acceleration reached respectively 1.97 mm and 0.0244 g at DT1. Under shut off of the TMDs, the maximum displacement and maximum acceleration increased slightly with respective values of 2.05 mm and 0.0316 g for LC4. Since LC4 repre-

Table 5. Characteristics of vertical TMD.

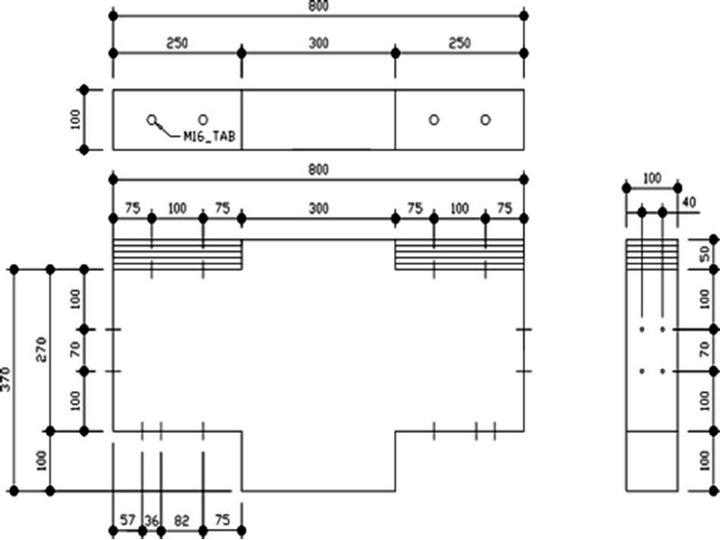
Figure 9. Dimension and view of TMD.

Figure 10. Walking test (numerous pedestrians running).

Figure 11. Walking test (2 pedestrians jumping).
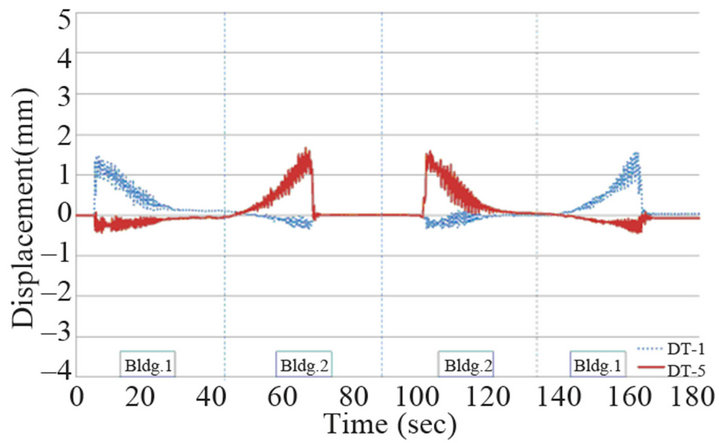 (a)
(a)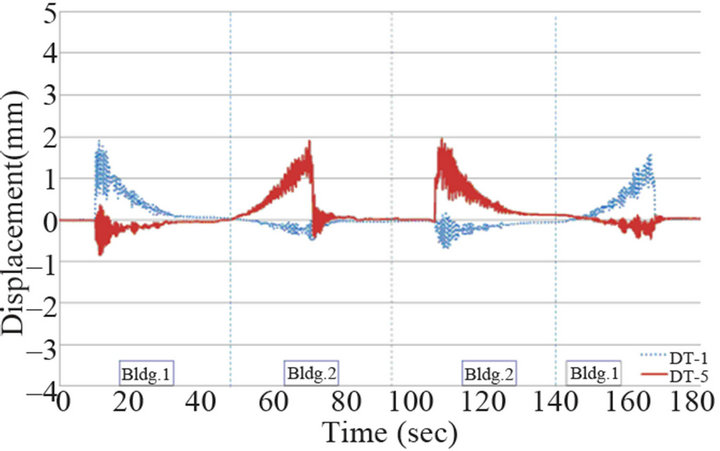 (b)
(b)
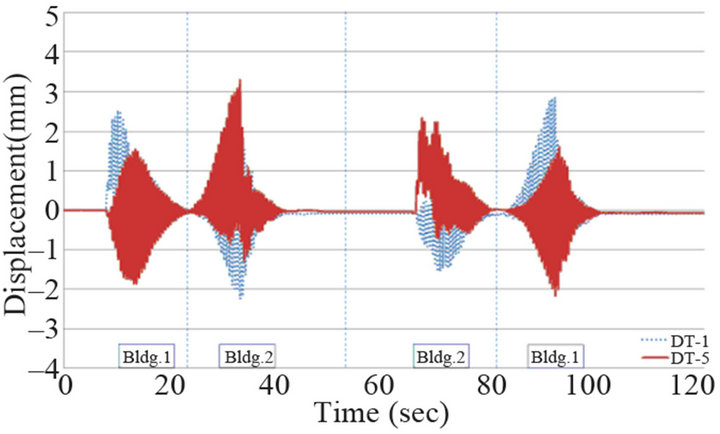
Figure 12. Displacement response (2 pedestrian walking): (a) TMD on; (b) TMD off.
 (a)
(a)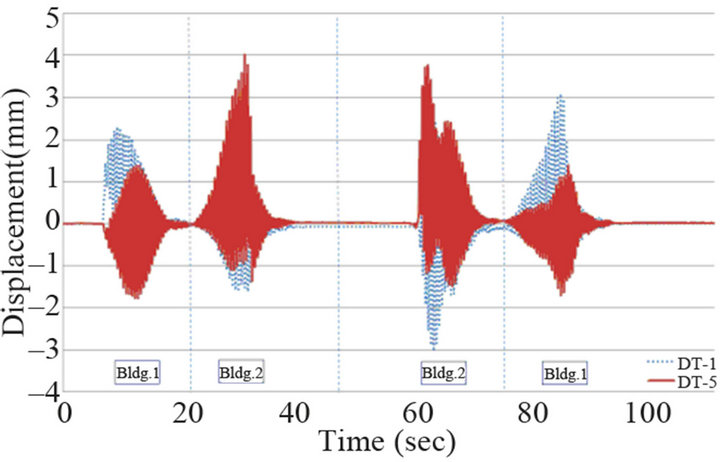 (b)
(b)
Figure 13. Displacement response (2 pedestrian walking rapidly): (a) TMD on; (b) TMD off.
 (a)
(a)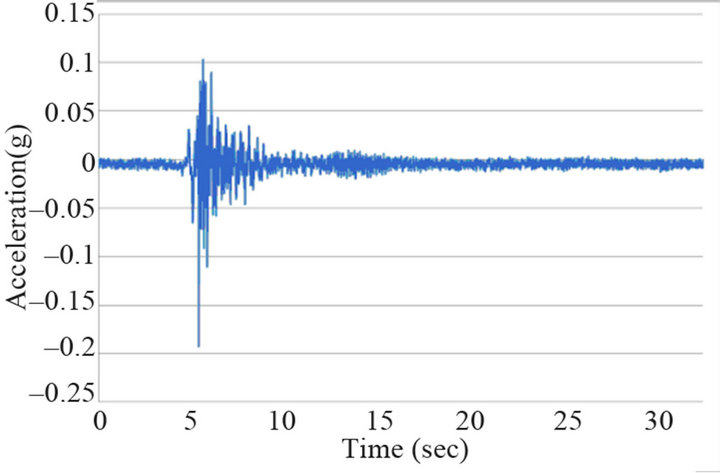 (b)
(b)
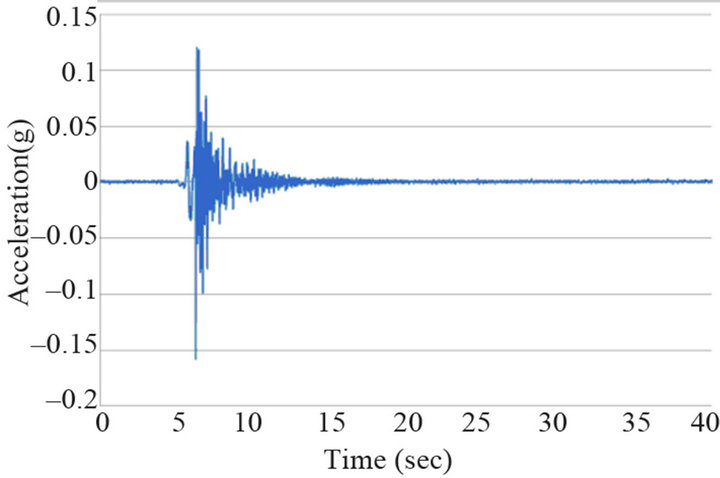
Figure 14. Acceleration response (2 pedestrian jumping): (a) TMD on; (b) TMD off.
sents the most common way of walking, the maximum acceleration can be said to be 0.0244 g falling below the limit value. In the future, more detailed analysis related to the serviceability of the UHPC pedestrian cable stayed bridge needs to be performed.
7. Conclusion
A pedestrian cable stayed bridge using 200 MPa class UHPC developed by KICT has been designed and erected for the first time in the world. KICT-UHPC with a design compressive strength larger than 180 MPa can resist to large compressive forces and is a material enabling to minimize the thickness of the cross-section owing to its large resistance to tension and shear. Besides, UHPC is also featured by large autogenous shrinkage which presents the risk of early cracking in the case of structures with complex shape. Considering these characteristics of UHPC, the pedestrian UHPC cable stayed bridge was constructed in the site of KICT. Measures to prevent the occurrence of early autogenous shrinkage cracks were derived through a trial construction and the dynamic characteristics of UHPC members were evaluated by means of static loading tests on full-scale specimens. These findings enabled to verify the applicability of UHPC not only to pedestrian cable stayed bridges but also to common highway cable stayed bridge structures. In-depth tasks for further studies were also derived. In addition, a first series of forced vibration tests made it possible to evaluate the dynamic characteristics of the pedestrian bridge through measurement of its natural frequency, vibrational acceleration and dynamic displacement responses. The test results revealed that the pedestrian bridge secures satisfactory dynamic characteristics for most of the load cases. However, responses appeared to exceed the limit values in the case of jumping impact by users. Accordingly, TMDs were installed on the parapet of the pedestrian bridge to reduce vibration. Verification tests showed that the maximum acceleration response of 0.186 g measured before the installation of the TMDs under standing jump of two people reduced effectively by more than 49% to drop down to 0.095 g after the installation of the TMDs and fell within the limit value of 0.1 g. Moreover, the vibration effect reducing effect of the TMDs could also be verified in the case of 2 people walking at regular pace by a decrease of 30% of the maximum acceleration response from 0.0316 g to 0.0244 g. Future studies will apply various test variables for diversified vibration tests and analyses to evaluate the vibrational characteristics of the pedestrian bridge such as the maximum acceleration, dynamic deflection and mode shapes. Furthermore, it is believed that reliable data related to the vibration serviceability of the pedestrian cable stayed bridge according to the installed TMDs could be secured through more precise verification tests, dynamic analyses and lateral vibration tests.
8. Acknowledgements
This research was supported by a grant from a Strategic Research Project (Development of design and construction system technology for hybrid cable stayed bridge) funded by the Korea Institute of Construction Technology.
REFERENCES
- Association Française de Génie Civil (AFGC), “Ultra High Performance Fibre-Reinforced Concretes—Interim Recommendations,” AFGC Scientific and Technical Documents, 2002.
- B. S. Kim, et al., “Design and Construction of Innovative UHPC Pedestrian Cable Stayed Bridge in Korea,” 33rd IABSE Symposium: Sustainable Infrastructure Environment Friendly, Safe and Resource Efficient, Bangkok, 9- 11 September 2009.
- H. Park, et al., “Model-Based Optimization of Ultra High Performance Concrete Highway Bridge Girders,” CEE Report R03-01, Cambridge, Massachusetts Institute of Technology, 2003.
- Federal Highway Association (FHWA), “High Performance Concrete Structural Designers’ Guide,” 2005.
- Japan Society of Civil Engineers (JSCE), “Tentative Guidelines for the Design and Construction of UHPC FiberReinforced Concrete,” 2004.
- Korea Institute of Construction Technology (KICT), “Report of R&D on the Design and Construction of Hybrid Cable Stayed Bridge,” 2009
- Y. J. Kim, et al., “A Study on Vibration Control of UHPC Pedestrian Cable Stayed Bridge,” 5th HPSM, Tallinn, 26-28 July 2010.
- J. I. Lee, “Efficient Vibration Control of Footbridge Using TMD,” Proceedings of KSCE Annual Conference, Pyeong-chang, 2002.

