Engineering
Vol. 3 No. 12 (2011) , Article ID: 9206 , 11 pages DOI:10.4236/eng.2011.312146
Investigation of Self Excited Torsional Vibrations of Different Configurations of Automatic Transmission Systems during Engagement
Faculty of Engineering, Helwan University, Cairo, Egypt
E-mail: eladlmr@yahoo.com
Received March 23, 2011; revised April 18, 2011; accepted May 10, 2011
Keywords: Self Excited, Torsional Vibration, Computer Simulation, Ravigneaux Planetary Gear Set, Compound Planetary Gear Set, Longitudinally Mounted Automatic Transmission
ABSTRACT
The vehicle drive line system is subjected to torsional vibration from different sources of the system such as, engine fluctuating torque, Hook’s joint and the final drive. However, the essential source is the friction torque induced in the friction elements, during their engagement. In the automatic transmission system, the planetary gear set includes several friction elements such as; clutch, band brakes, and one way clutch. During the engage-ment, severe torsional vibration is induced by friction which is noticeable by the passen-gers in the form of what so called vehicle shunt. In present paper, a torsional vibration model for Drive Line (DL) system includes three different configurations of automatic transmission is constructed. A computer program using MATLAB subroutines is impleme-nted to obtain the system response. Effect of system parameters on the dynamic behavior and stability has been investigated. The system damping and the trend of the friction coefficient have an essential effect on the dynamic behavior and stability of the system. The system response is now predictable with change of the system parameters which opens up the opportunity in future to control the vibration level.
1. Introduction
Vehicle transmission noise and vibration constitute a serious problem in the driveline system [1,2], which is concerned in the present study. Investigation of the torsional vibration characteristics of a transmission is simplified if the actual system is firstly replaced by a dynamically equivalent one. In the torsional vibration equivalent system, all shafts and masses (gears) rotate with the same mean angular velocity. It is usual to select one of the shafts of the original system as a reference shaft and to refer all quantities to the speed of this shaft. The kinetic and strain energies in every element in the equivalent system must be equal to that in the corresponding element in the original system. Certain parts in the transmission revolve without transmitting torque. These parts are not subjected to torsional load and considered as inertias only. The oscillating torque and torsional displacement of the system can be obtained by solving the governing equations of motion of the equivalent system. The overall equivalent torsional vibration model consists of idealizing the complete DL system as a set of inertia discs linked together by torsional, linear and massless, springs which reproduce the dynamic behavior of all constituent parts [3]. The interest of this paper is to model and investigate the main sources of excitation of the torsional vibrations of a DL system includes in an automatic transmission. Detection of the automatic transmission torsional vibration sources (clutches, band brakes, and one way clutches) during the gear change is considered for three different types of automatic transmission. Namely; Ravigneaux planetary gear set, compound planetary gears set, longitudinally mounted four speed planetary gear set. The effect of the system design parameters on its dynamic behavior and stability is concerned.
2. Ravigneaux-Planetary Gear Set Models
A Ravigneaux system consists of two planetary gear sets as; single-pinion simple planetary gear set and double pinion planetary gear set. The original system of Ravigneaux-planetary gear system is shown in Figure 1. In the first set, the sun gear is located in the centre meshing with two or more long planet-pinion gears. The planetary gears are pivoted to the planetary carrier plate. The carrier shaft rotates carrying the planet pinions around in a circle. An internal gear or a ring gear is also meshed with the planetary gears pinion. Therefore, the first set has three members. The three members are; the sun gear, the planet-pinion carrier and the ring gear. The Second set consists of a small sun gear, several short planet-pinion gears, the ring gear, the long planet-pinion gears and the planetary carrier which are shared with the first set [4].
2.1. Equivalent System
Ravigneaux original system has been converted to an equivalent one as shown in Figure 2. The equivalent system represents; the engine and pump mass moment of inertia  exposed to the engine fluctuating torque
exposed to the engine fluctuating torque , turbine mass moment of inertia
, turbine mass moment of inertia , exposed to the turbine excitation torque
, exposed to the turbine excitation torque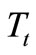 , mass moment of inertia of planetary gear set
, mass moment of inertia of planetary gear set 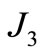 excited by clutch or brake torque
excited by clutch or brake torque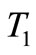 , torsional stiffness of the input shaft
, torsional stiffness of the input shaft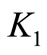 , and torsional stiffness of the output shaft
, and torsional stiffness of the output shaft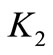 . The fixed end represents the inertia of the vehicle body. The torsional spring
. The fixed end represents the inertia of the vehicle body. The torsional spring 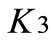 represents the stiffness of the rest of the DL.
represents the stiffness of the rest of the DL.
2.2. Equation of Motion of Torsional Vibration Model
The torsional vibration equation of motion of the model, Figure 2, is derived in the matrix form [1] as;
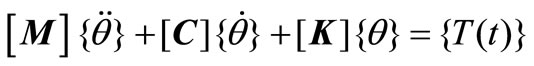
where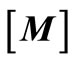 ,
,  , and
, and 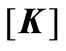 are system mass, damping, and stiffness matrices respectively.
are system mass, damping, and stiffness matrices respectively.
The equivalent system matrices obtained using Lagrange’s equation
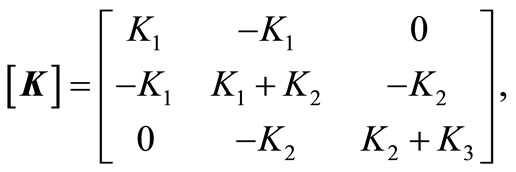
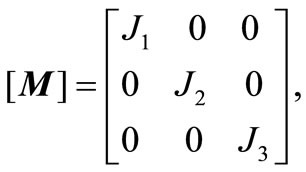
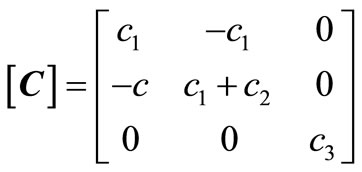
The form of the excitation torque vector 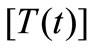 and the equivalent moment of inertia
and the equivalent moment of inertia  depend on the gear shift.
depend on the gear shift.
2.3. First Gear Shift
In the first gear shift, the clutch cl2, Figure 1, is applied to transmit the engine torque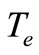 , and consequently the turbine torque
, and consequently the turbine torque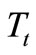 , are transmitted to the forward sun gear (
, are transmitted to the forward sun gear (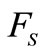 ) through the clutch cl2. The forward sun gear direction (
) through the clutch cl2. The forward sun gear direction ( ) rotates in clockwise causing counterclockwise rotation of the short pinion (
) rotates in clockwise causing counterclockwise rotation of the short pinion (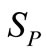 ). The carrier (
). The carrier (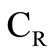 ) is held by the 1-2 one way clutch (1-2 OWC), which makes the ring gear (
) is held by the 1-2 one way clutch (1-2 OWC), which makes the ring gear (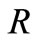 ) rotates around its axis in clockwise direction. Torque is transmitted from the forward sun gear to the output shaft; then to the ring gear. The system excitation torque vector becomes [5-7];
) rotates around its axis in clockwise direction. Torque is transmitted from the forward sun gear to the output shaft; then to the ring gear. The system excitation torque vector becomes [5-7];

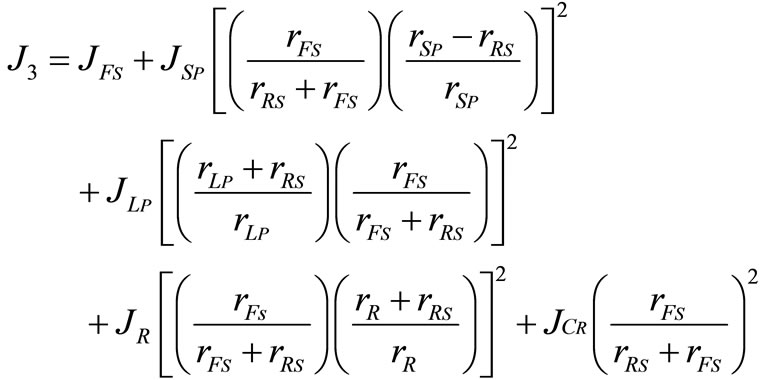
2.4. Equivalent Inertia of Planetary Gear Set
The equivalent inertia of the planetary gear set (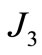 ) can be obtained by equating the kinetic energies of the original gear set and the equivalent one. The kinetic energy of the gear set of the original system is:
) can be obtained by equating the kinetic energies of the original gear set and the equivalent one. The kinetic energy of the gear set of the original system is:
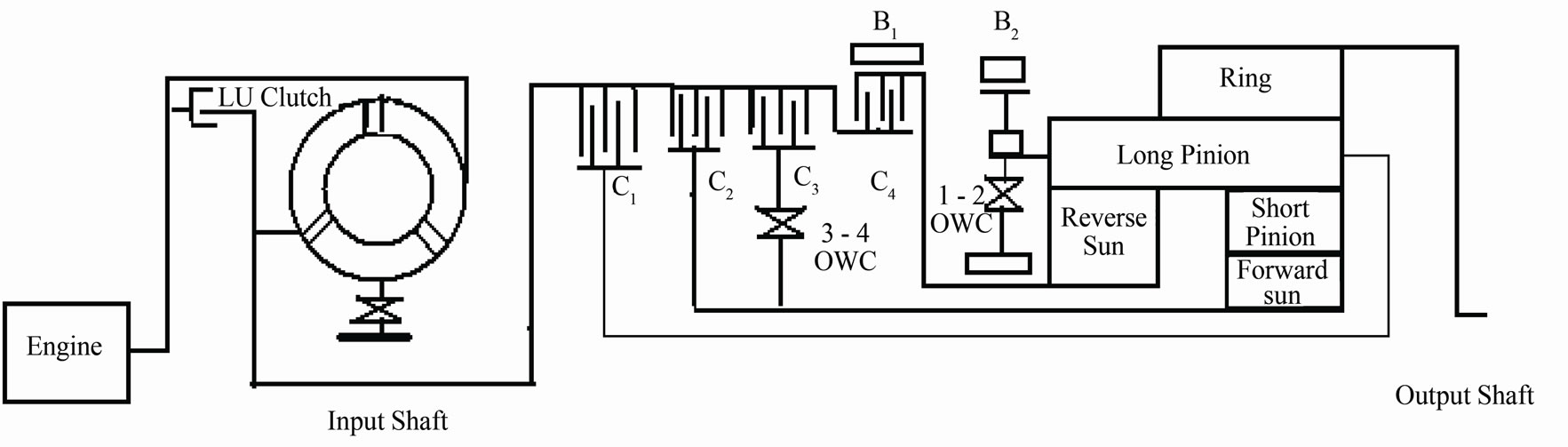
Figure 1. Original system of ravigneaux.

Figure 2. Equivalent system.
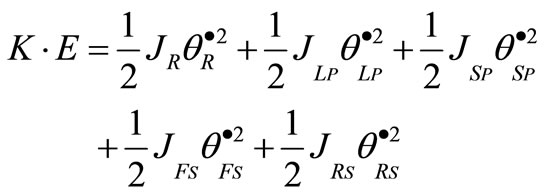
where the subscripts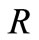 ,
, ,
,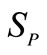 ,
,  and
and  denote ring gear, long pinion, short pinion, forward sun gear, and reverse sun respectively. Putting the kinetic energy in terms of
denote ring gear, long pinion, short pinion, forward sun gear, and reverse sun respectively. Putting the kinetic energy in terms of 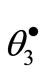 and equating the kinetic energy of original and equivalent systems, the equivalent mass moment of inertia of the gear set is obtained as follows,
and equating the kinetic energy of original and equivalent systems, the equivalent mass moment of inertia of the gear set is obtained as follows,
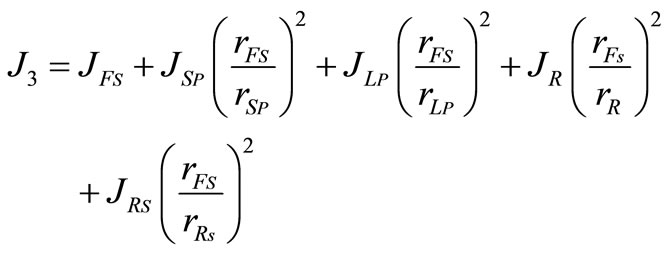
The clutch torque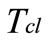 , assuming uniform wear [8]; The friction clutch torque in terms of angular perturbbation is;
, assuming uniform wear [8]; The friction clutch torque in terms of angular perturbbation is;
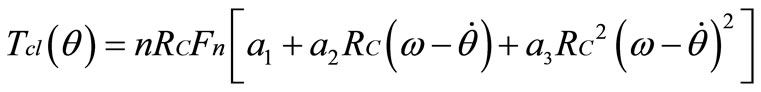
The Reaction torque of the one-way clutch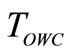 , [7]; The reaction torque of the one-way clutch decreases as the band brake torque increases because the constants
, [7]; The reaction torque of the one-way clutch decreases as the band brake torque increases because the constants  and
and 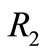 are negative and positive values respectively.
are negative and positive values respectively.
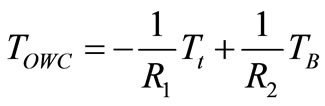
Turbine torque of the torque converter 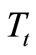 [8]; The torque ratio of the torque converter is considered a basic parameter to define the torque converter performance. The following equations represent these relationships with and without lock-up clutch.
[8]; The torque ratio of the torque converter is considered a basic parameter to define the torque converter performance. The following equations represent these relationships with and without lock-up clutch.
without lock-up clutch, 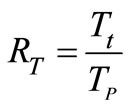
with lock-up clutch, 
where 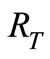 = Torque ratio.
= Torque ratio. 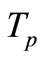 = Pump torque.
= Pump torque.  = Engine torque.
= Engine torque.
The band brake torque 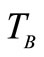 [8]; There are two expressions of the band brake friction torque according to engagement mode as;
[8]; There are two expressions of the band brake friction torque according to engagement mode as;
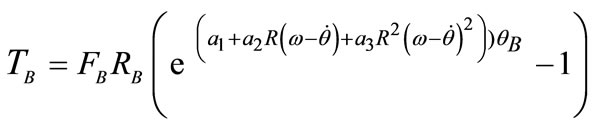
In the de-energized mode:
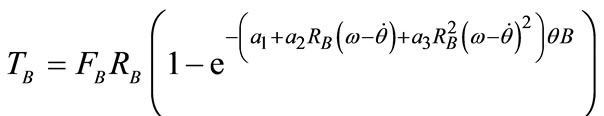
2.5. Second Gear Shift
In the second gear shift, the clutch cl2, Figure 1, is applied to transmit the engine torque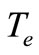 , and consequently the turbine torque
, and consequently the turbine torque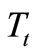 , is transmitted to the forward sun gear (
, is transmitted to the forward sun gear ( ) through the clutch cl2. The clockwise rotation of
) through the clutch cl2. The clockwise rotation of  causes counter clockwise rotation of the short pinion (
causes counter clockwise rotation of the short pinion (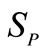 ) around the carrier. The reverse sun gear (
) around the carrier. The reverse sun gear (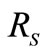 ) is held by the band brake (B1), which makes the long pinion (
) is held by the band brake (B1), which makes the long pinion (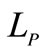 ) rotates clockwise around reverse sun gear and ring gear (
) rotates clockwise around reverse sun gear and ring gear (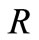 ) rotates around its axis in clockwise direction. Torque is transmitted from
) rotates around its axis in clockwise direction. Torque is transmitted from 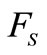 to the output shaft which splinted in the ring gear. The system excitation torque vector becomes [5,6];
to the output shaft which splinted in the ring gear. The system excitation torque vector becomes [5,6];
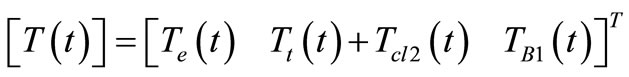
As the first gear shift, the equivalent mass moment of inertia of the gear set ( ) is obtained from equating the kinetic energy of the original and equivalent systems as;
) is obtained from equating the kinetic energy of the original and equivalent systems as;
3. Compound Planetary Gears Set
A compound system consists of two simple planetary gear sets is considered in this section. The original system of the compound planetary gear system is shown in Figure 3. Each set has three members as an input and
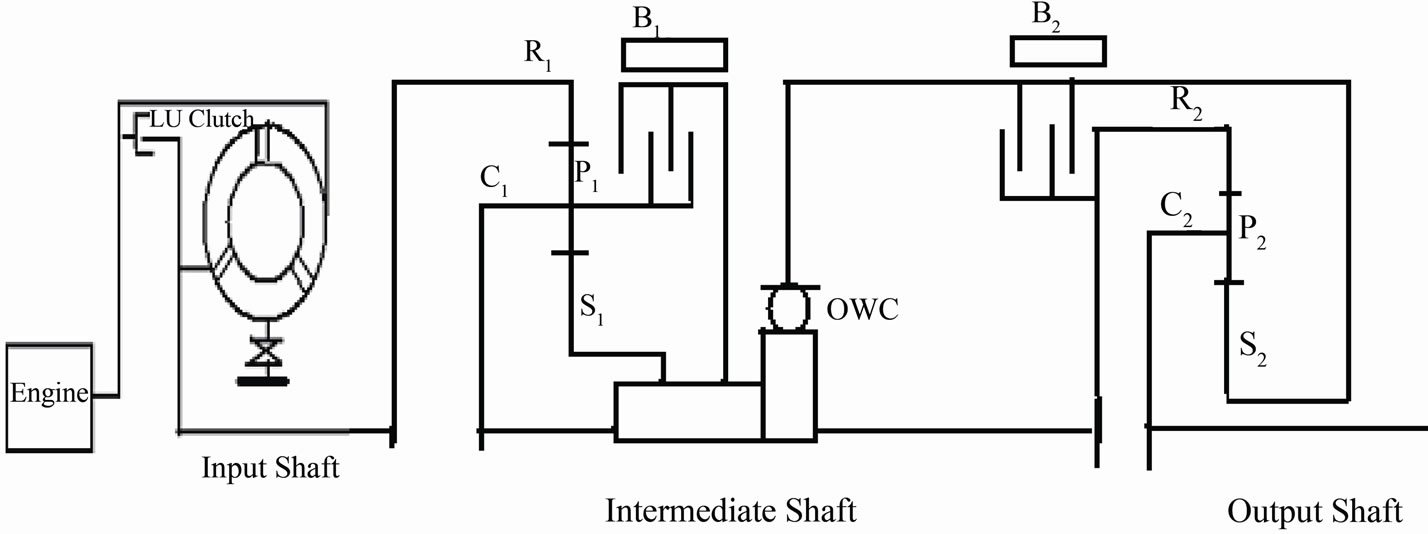
Figure 3. Original system of compound planetary gears set.
output for the system power. The first set has the sun gear (S1), the planet-pinion carrier (CR1) and the ring gear (R1), while the second set has the sun gear (S2), the planet-pinion carrier (CR2) and the ring gear (R2). In this compound system the transmission input shaft is the ring gear (R1) shaft, and the output shaft is the planet-pinion carrier (CR2) shaft [9,10].
3.1. Equivalent System
Original system of the compound planetary gear system has been converted to an equivalent one shown in Figure 4. The torsional vibration parameters for the equivalent system of the compound planetary gear system are the same as the torsional vibration parameters for the equivalent system of Ravigneaux planetary gear system except the mass moment of inertia of second planetary gear set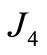 , with clutch or brake excitation torque
, with clutch or brake excitation torque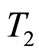 , torsional stiffness of the intermediate shaft
, torsional stiffness of the intermediate shaft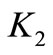 , and torsional stiffness of the output shaft
, and torsional stiffness of the output shaft .
.
The equivalent system matrices obtained using Lagrange’s equation are;

The excitation torque vector and equivalent mass moment of inertia 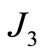 and
and 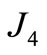 depend on the gear shift.
depend on the gear shift.
3.2. First Gear Shift
In the first gear shift, both band brakes (B1) and (B2) are applied, which hold the first sun gear (S1) and second sun gear (S2). The turbine torque 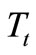 is transmitted to the first ring gear (R1). The clockwise rotation of the first ring gear causes clockwise rotation of the first pinion (P1) which causes clockwise rotation of the carrier (CR1). The torque is transmitted from carrier (CR1) to second gear set input shaft through the second ring gear (R2). Then the torque is transmitted to the pinion gear (P2), causing clockwise rotation of the carrier (CR2) which is connected to the output shaft. The excitation torque vector source is [5,6];
is transmitted to the first ring gear (R1). The clockwise rotation of the first ring gear causes clockwise rotation of the first pinion (P1) which causes clockwise rotation of the carrier (CR1). The torque is transmitted from carrier (CR1) to second gear set input shaft through the second ring gear (R2). Then the torque is transmitted to the pinion gear (P2), causing clockwise rotation of the carrier (CR2) which is connected to the output shaft. The excitation torque vector source is [5,6];

From equating the kinetic energy of the original gear set and the equivalent one, the equivalent mass moment of inertia of the first gear and second sets are obtained as,
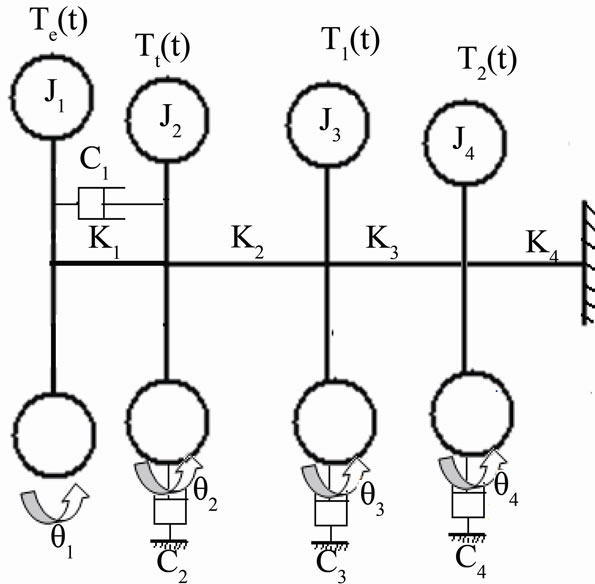
Figure 4. Equivalent system.
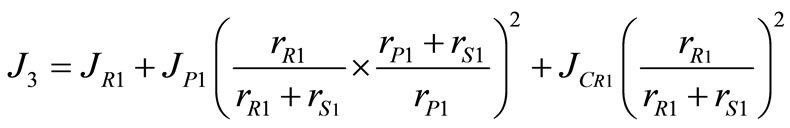
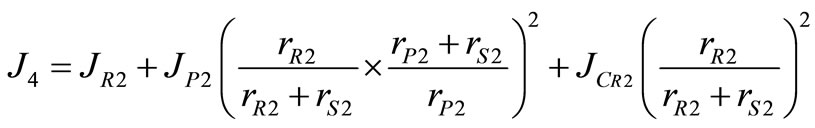
3.3. Second Gear Shift
In the second gear shift, the clutch (cl1) is applied and the first gear set rotates as one part then the output torque is transmitted to the second gear set with speed ratio (1:1). The second sun gear is held by band brake (B2); the torque is transmitted to the second ring gear (R2). The clockwise rotation of the second ring gear causes clockwise rotation of the second pinion (P2) around the carrier causes a clockwise rotation the carrier (CR2) and then the torque is transmitted to the output shaft. The system excitation vector is [5,6];
The equivalent mass moment of inertia of the first and second gear sets are obtained as;
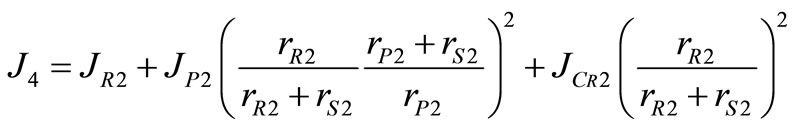
4. A Longitudinally Mounted Four Speed Automatic Transmission
This system consists of thee planetary gears sets. Each set has three members as the input and output for the system power. The first and second sets have the same components as in the compound system. The third set has the sun gear (S3), the planet-pinion carrier (CR3) and the ring gear (R3). The original system of the longitudinally mounted four speed automatic transmission system is shown in Figure 5 [11].
4.1. Equivalent System
The original system of this system was converted to an equivalent one as shown in Figure 6. The torsional vibration parameters for the equivalent system of the longitudinally mounted four speed automatic transmission system are the same as the torsional vibration parameters for the equivalent system of the compound planetary gear system except the mass moment of inertia of the third planetary gear set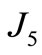 , with clutch or brake excitation torque
, with clutch or brake excitation torque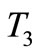 .
.
The equivalent system matrices obtained using Lagrange’s Equation are;

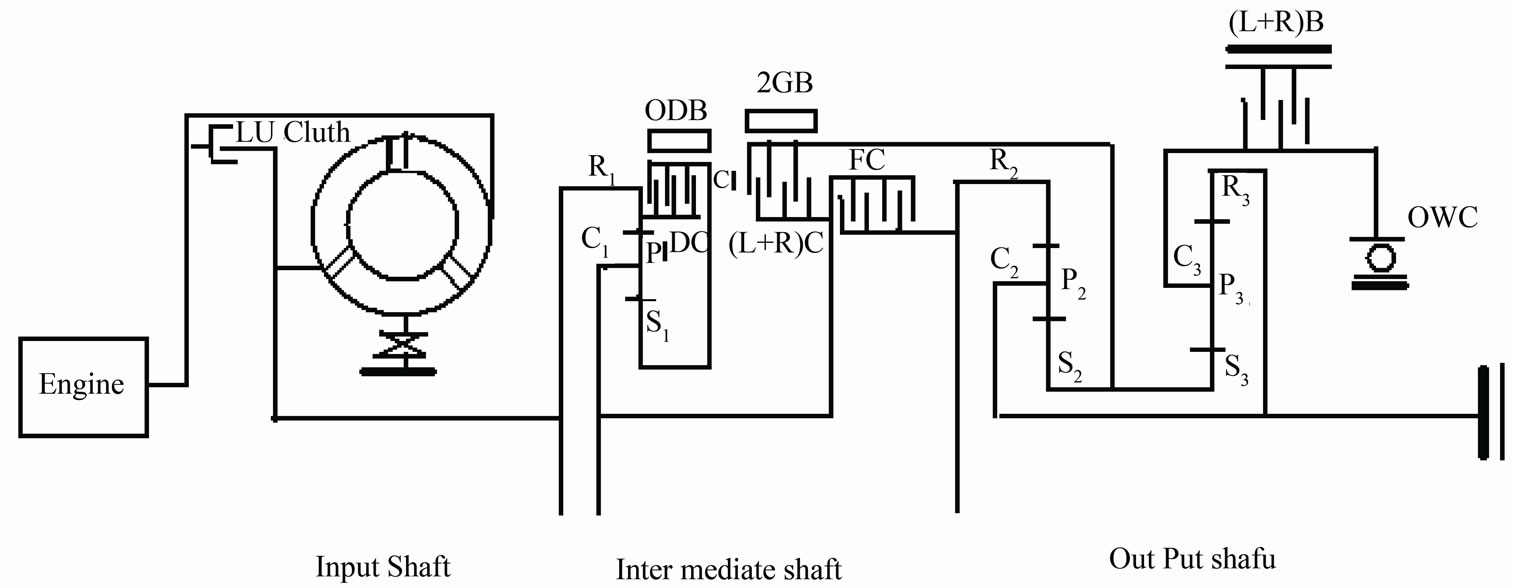
Figure 5. Original system of a longitudinally mounted.
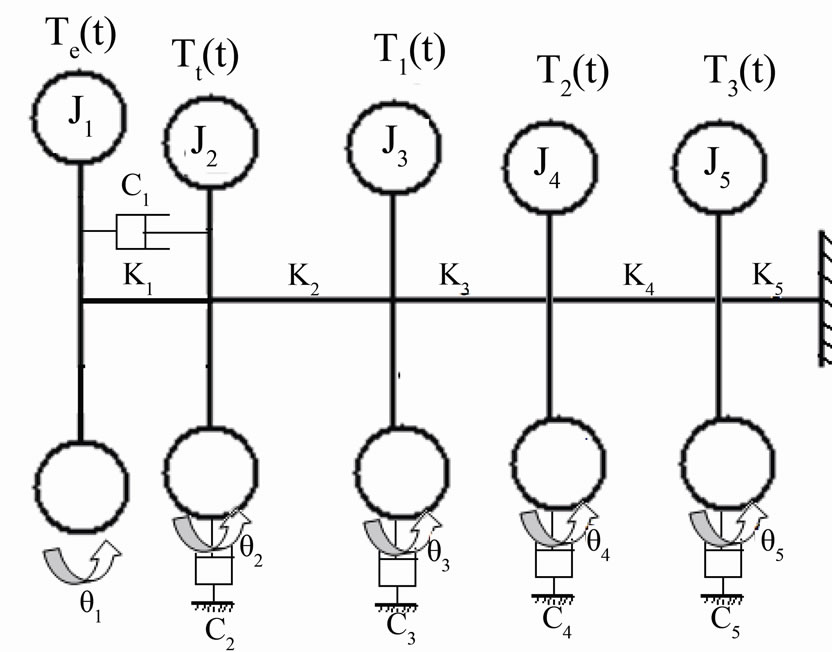
Figure 6. Equivalent system.
4.2. First Gear Shift
The engine torque is transmitted to the overdrive pinion gears via the output shaft and the pinion carrier. Torque is then splitted between the overdrive annular gear and sun gear, both paths merging due to the engaged direct clutch (cl1). Therefore the overdrive pinion gears are prevented from rotating on their axes, causing the overdrive gear set reduction ratio at this stage. The torque is then conveyed from the overdrive annular gear to the intermediate shaft where it passes through the applied forward clutch plates (cl3) to the annular gear of the forward gear set. The clockwise rotation of the forward annular gear causes the forward planet gears to rotate clockwise, driving the double sun gear counter clockwise. the forward planetary carrier attached to the output shaft so that the planet gears drive the sun gear instead of walking around the sun gear. This anticlockwise rotation of the sun gear causes the reverse planet gears to rotate clockwise. With the One Way roller Clutch (OWC) holding the reverse planet carrier, the reverse planetary gears turn the reverse annular gear and the output shaft clockwise in low speed ratio. The system excitation torque vector is [5-7];
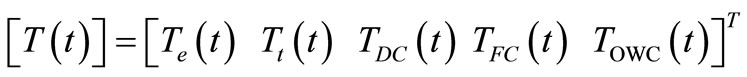
As the previous system, the equivalent mass moment of inertia of the over drive, the forward planetary and the reverse planetary gear sets are;
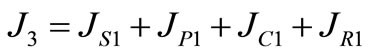
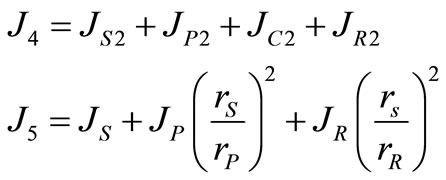
4.3. Second Gear Shift
The engine torque is transmitted through the locked overdrive gear set similarly to first gear. It is then conveyed through the applied forward clutch (cl3) via intermediate shaft to the forward annular gear. With the double sun gear held by applied second gear band brake (B2), the clockwise rotation of the forward annular gear compels the pinion gears to rotate on their own axes and roll around the stationary sun gear in a clockwise direction. Because the forward pinion gear pins are mounted on the pinion carrier, which is itself attached to the output shaft, the output shaft will be driven clockwise at a reduced speed ratio. The system excitation torque vector is [5,6];
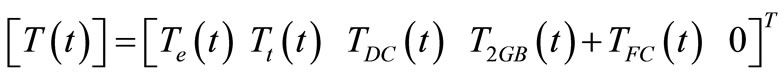
The equivalent mass moment of inertia of the over drive, the forward planetary and the reverse planetary gear sets are;
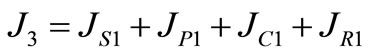

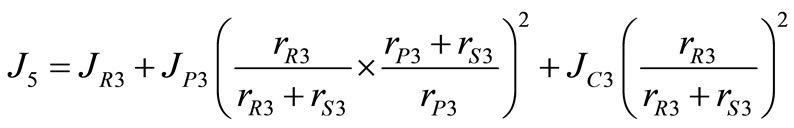
4.4. Results and Discussion
In this section, the fluctuating angular velocity of the gearbox output shaft for the three considered configuretions has been obtained. A computer program using MATLAB package has been implemented to solve the system equation of motion using Rung-Kotta method [8]. The program contains the torque of one-way clutch modeled as shown in Figure 7. Also, it includes the calculations of the coefficient of friction of the clutch and band brake, the described values of the axial force for the clutch engagement, and the accurate values of band brake. Consequently, clutch and band brake excitation torques are included.
4.5. A Ravigneaux-Planetary Gear Set
The model of this system has three degrees of freedom and all torsional vibration sources have been considered, Figure 2. The angular velocity perturbation of the output gearbox shaft due to the excitation torque induced by the friction during gear shift in the elements clutch cl2 and the OWC (in first shift) or in clutch cl2 and the band brake (in second shift). Typical results for the first shift are shown in Figure 8.
Increasing the gradient of friction coefficient of the friction elements causes instability of the system, as shown in Figure 9. This instability occurred because the energy dissipated by the damping system was less than the energy added to the system by the friction induced in the friction elements (clutch cl2 and OWC or band brakes B1).
Figure 10 shows the system fluctuation when increasing the system damping for the first gear shift; comparing the fluctuation level in Figures 8 and 10, the system fluctuation level is highly affected by the system damping.
The excessive decrease of the system damping causes higher fluctuation level in the system response, as shown in Figure 11.
Decreasing the damping and increasing the gradient of friction coefficient at the same time causes the system to start with small fluctuation level at the beginning of the engagement then becomes unstable, as shown in Figure 12.
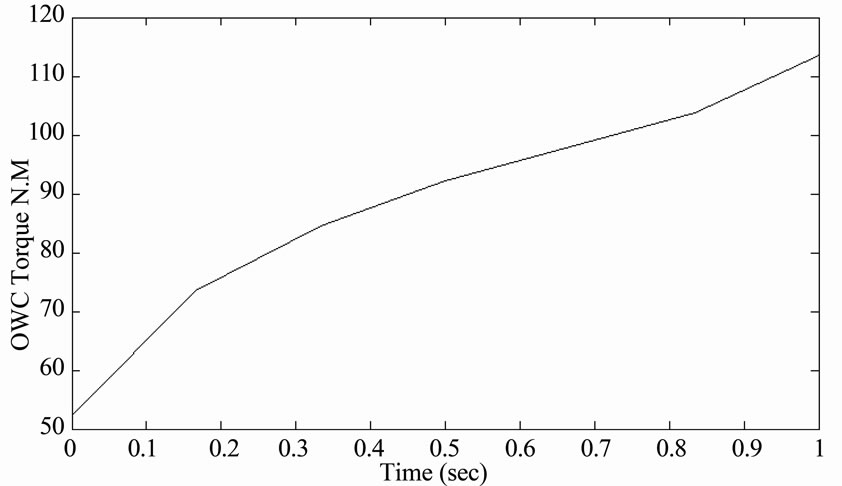
Figure 7. Torque of one-way clutch against engagement time.
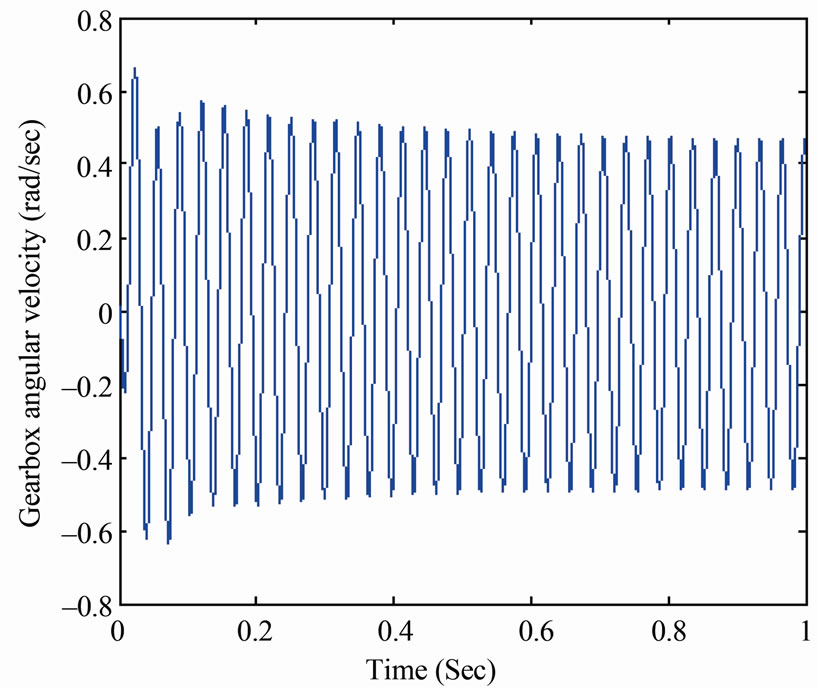
Figure 8. Gearbox output shaft response at the first gear shif.
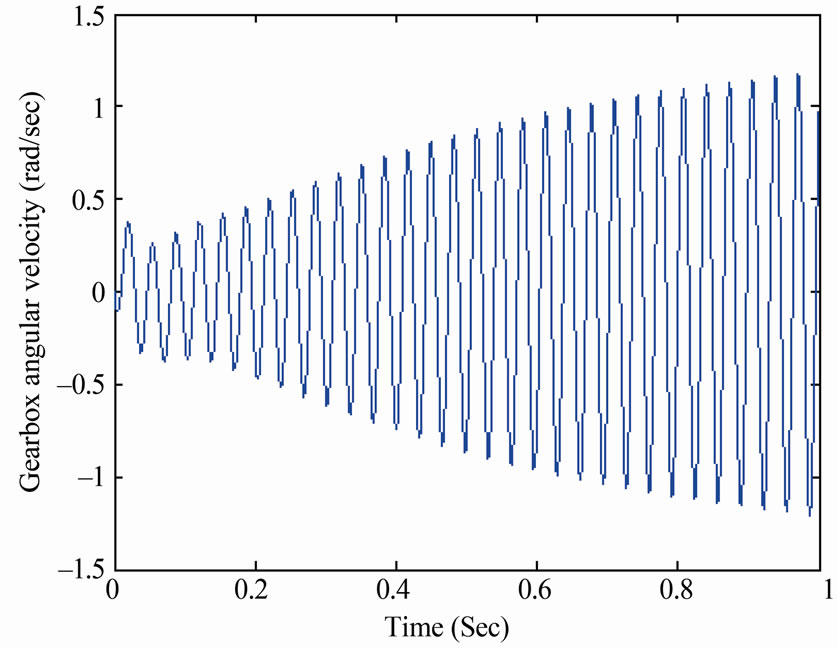
Figure 9. System response when increasing the gradient of friction coefficient at the first gear shift.

Figure 10. System response when increasing the damping at the first gear shift.
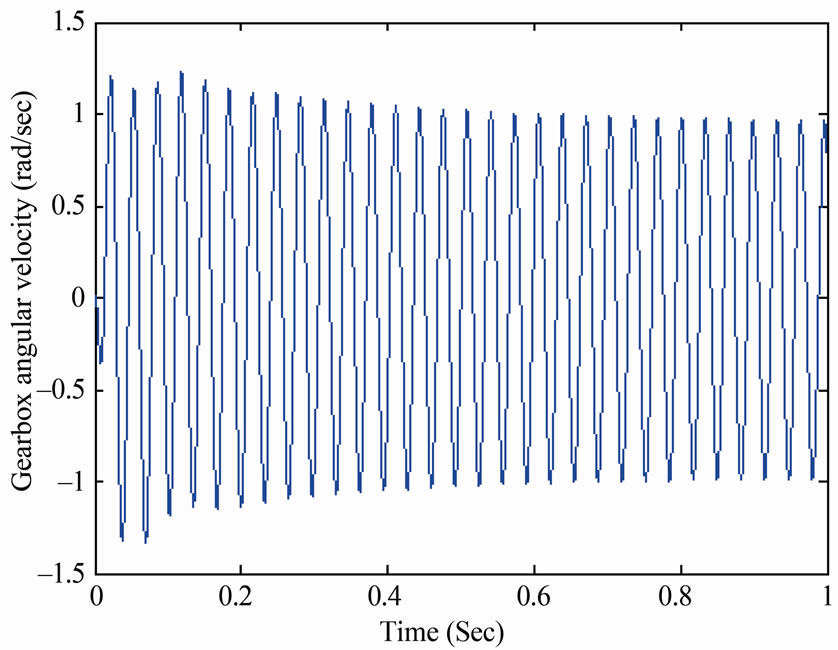
Figure 11. System response when decreasing the damping at the first gear shift.
Figure 12 System response when decreasing the system damping and gradient of friction coefficient at the first gear shift.
4.6. Compound Planetary Gears Set and Longitudinally Mount Four Speeds
The angular velocity perturbation of the output shafts of the compound and the longitudinally gearboxes are obtained as the system response due to the excitation torque induced in the friction elements during gear shift. The system response of the compound gearbox is nearly twice the longitudinally mounted one during both first and second shifts. Figures 13 and 14 show the system response during the first shifts for both configurations.

Figure 12. System response when decreasing the system damping and gradient of friction coefficient at the first gear shift.
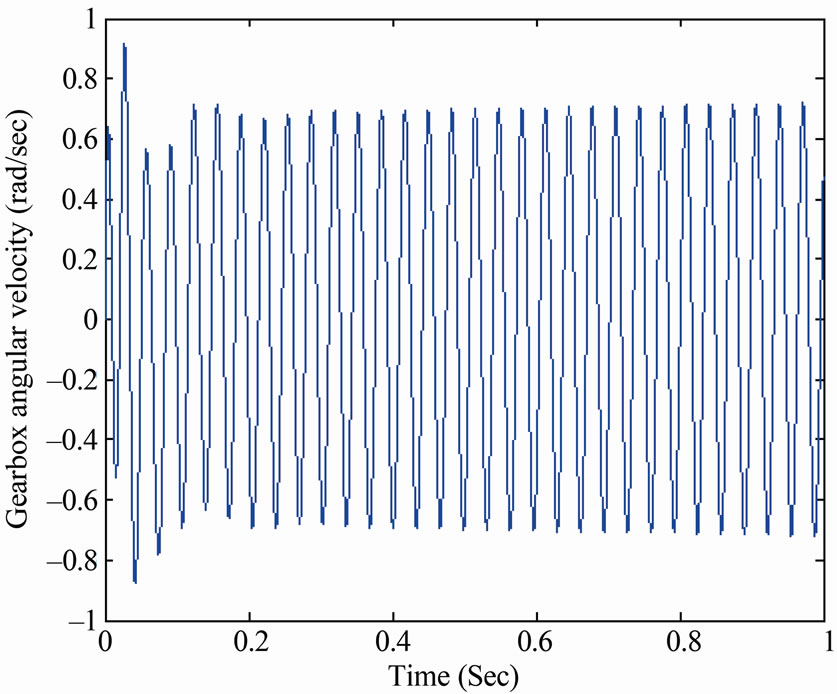
Figure 13. Compound Gearbox output shaft response at the first gear shift.
The system may become unstable at certain values of its parameters such as increasing gradient of friction coefficient and or decreasing damping. This flutter instability occurred because the energy dissipated by the damping system is less than the energy added to the system induced in the friction elements (band brakes or clutch or one way clutch). The compound gearbox is more sensitive to instability than the longitudinally mounted one at the first shift as shown in Figures 15 and 16 respectively.
The system fluctuation level is highly affected by the system damping. This is clear from comparing the fluctuation level in Figures 17 and 18 by the corresponding one in Figures 13 and 14.
Excessive decrease the damping causes higher fluctuation levels in the system response, Figures 19 and 20.
Decreasing the damping and/or increasing the gradient of friction coefficient at the same time causes low fluctuating in the system response at the beginning of engagement time then high fluctuation and instability occurs for

Figure 14. Longitudinally mounted four speed system response at the first gear shift.
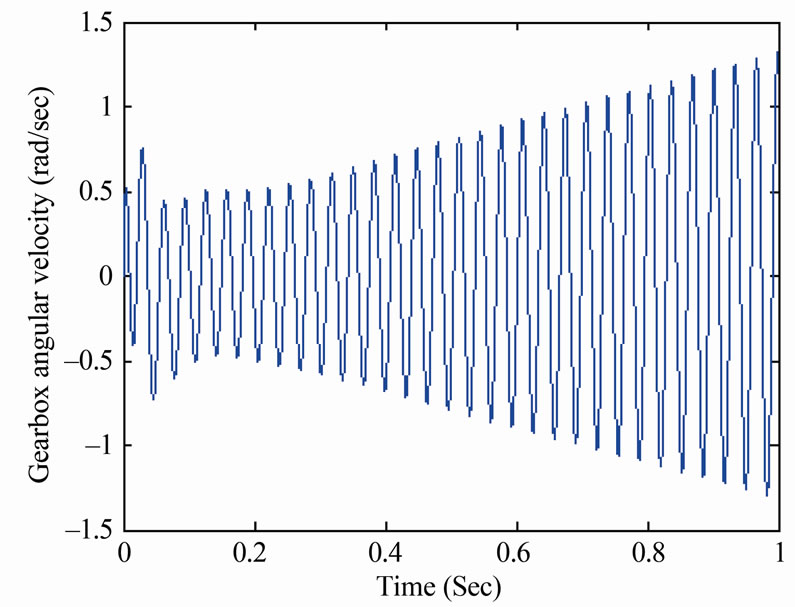
Figure 15. Compound gearbox system response when increaseing the gradient of friction coefficient at the first gear shift.
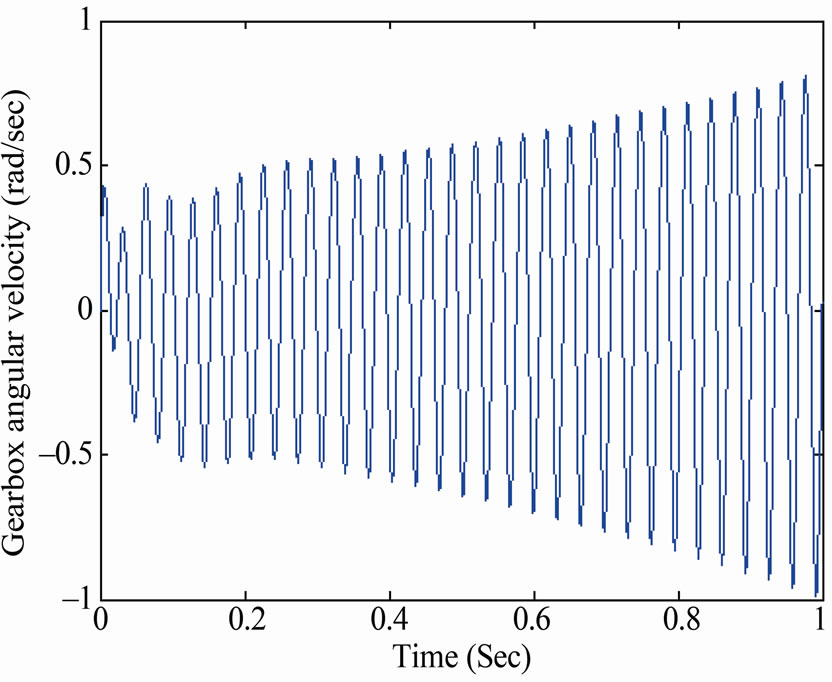
Figure 16. Longitudinally mounted four speed response when increasing the gradient of friction coefficient.
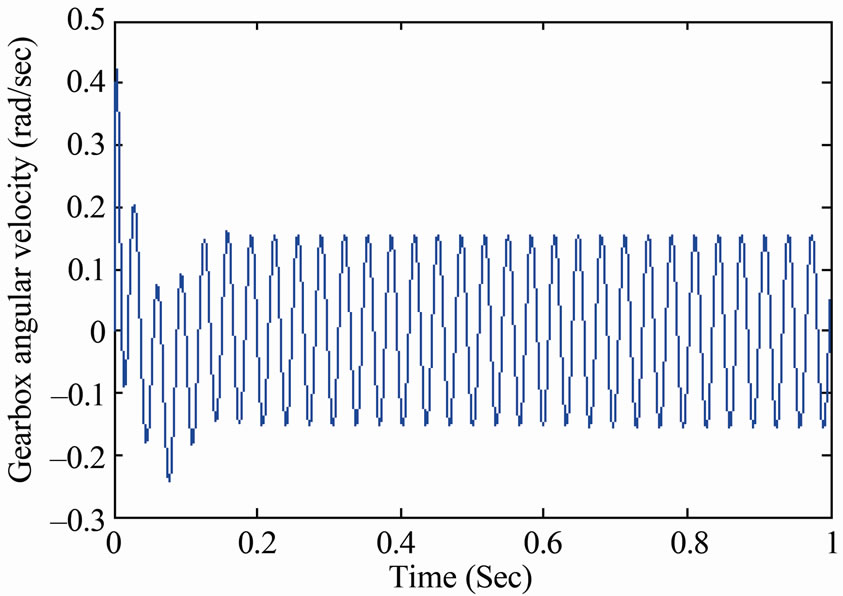
Figure 17. Compound gearbox system response when increasing the damping at the first gear shift.
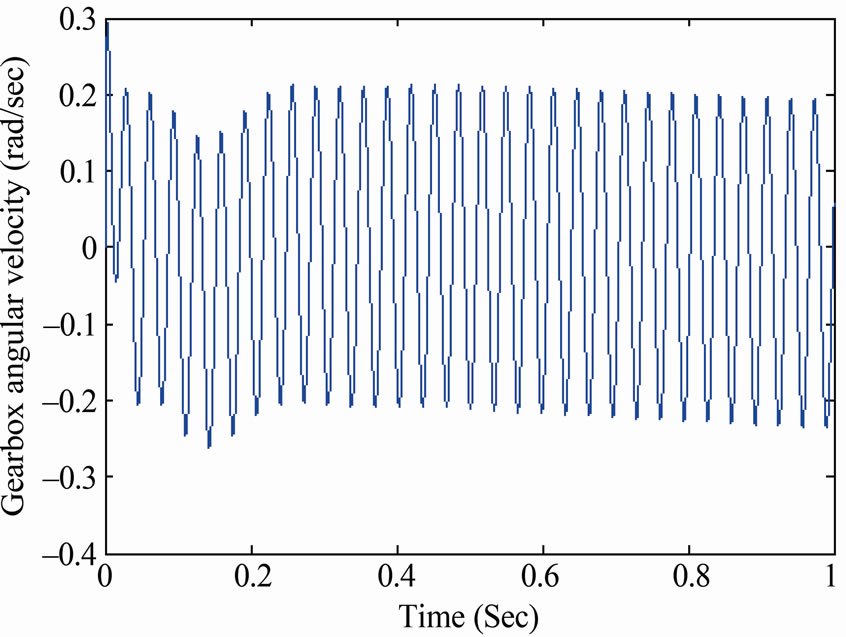
Figure 18. Longitudinally mounted four speed system response when increasing the damping at the first gear shift.
the two shifts and the two considered gearbox configuretions (compound and Longitudinal); as shown in Figures 21-24.
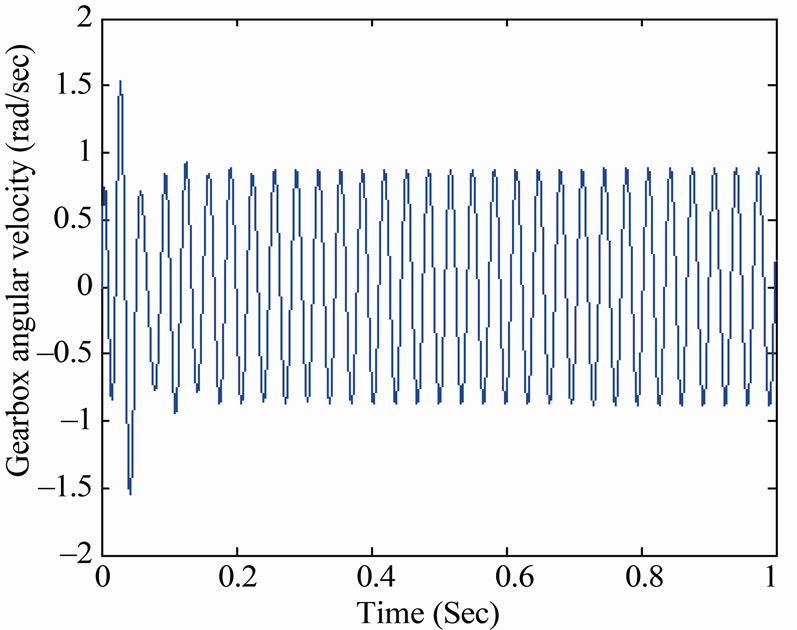
Figure 19. Compound gearbox system response when decreasing the damping at the first gear shift.
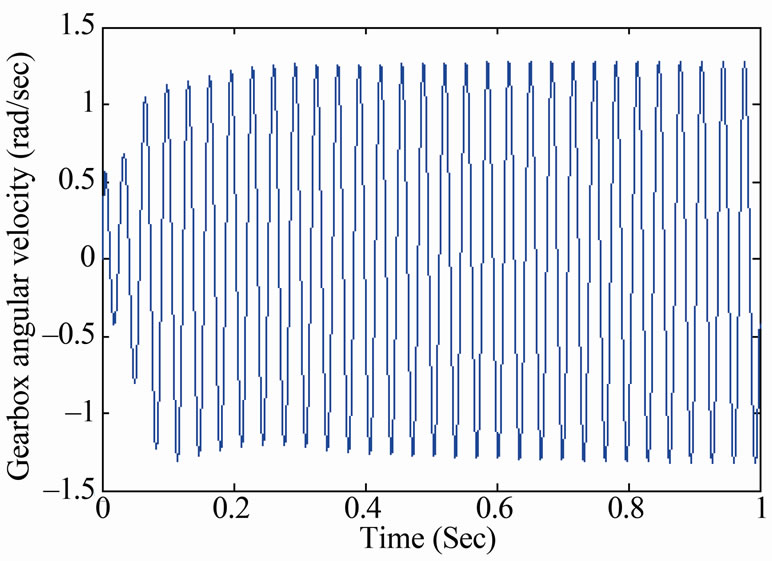
Figure 20. Longitudinally mounted four speed system response when decreasing the damping at the first gear shift.
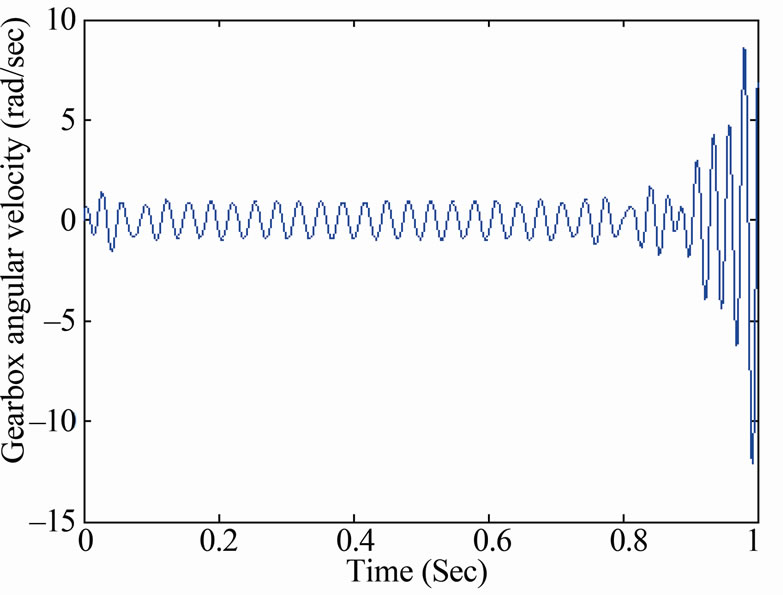
Figure 21. Compound gearbox system response when decreasing the damping and/or increasing gradient of the friction.
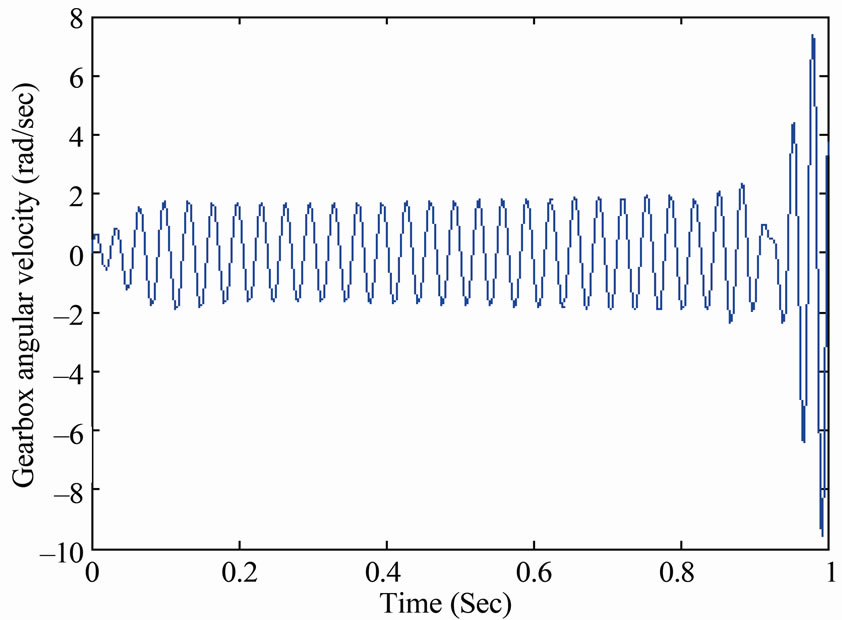
Figure 22. Longitudinally mounted four speed system response when decreasing the damping and/or increasing gradient of the friction coefficient at the first gear shift.
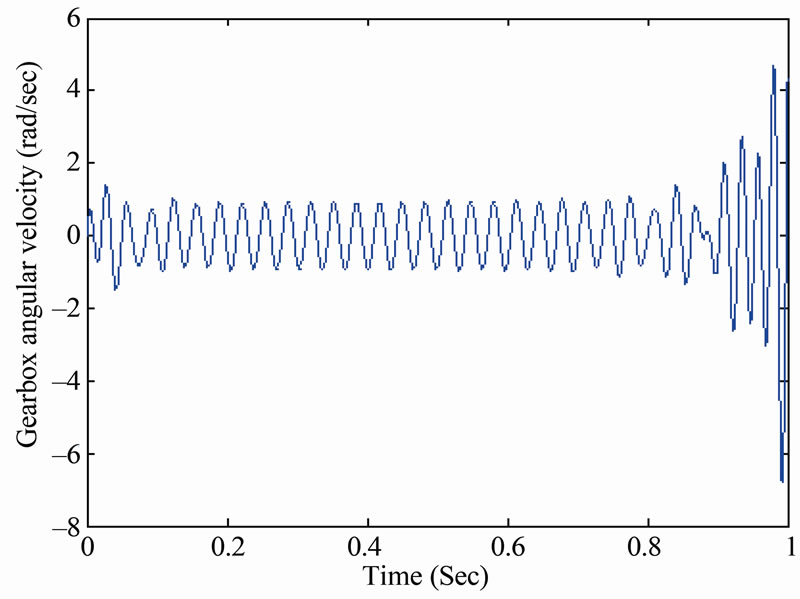
Figure 23. Compound gearbox system response when decreasing the damping and increasing gradient of the friction coefficient at the second gear shift.
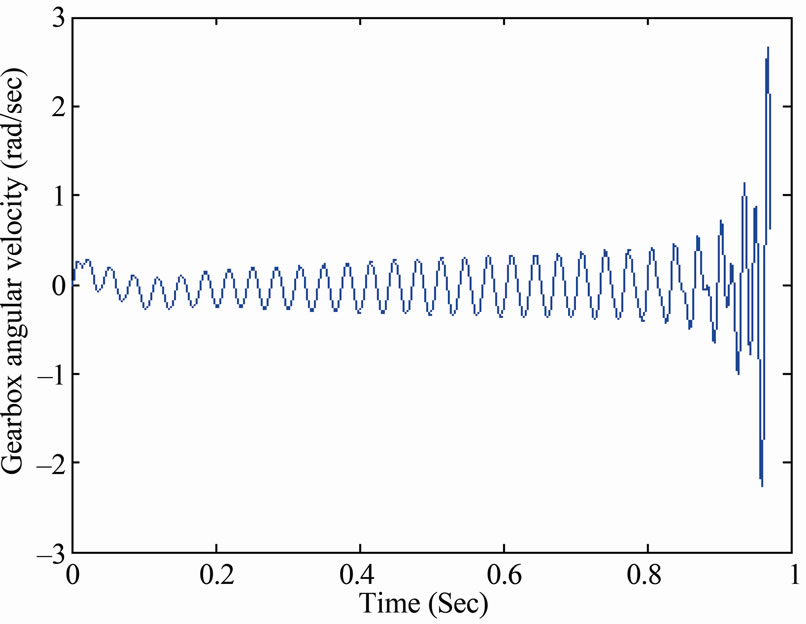
Figure 24. Longitudinally mounted four speed system response when decreasing the damping and/or increasing gradient of the friction coefficient at the second gear shift.
5. Conclusions
Mathematical models of torsional vibration of a vehicle drive line includes different configurations of automatic transmission systems have been constructed. The models include the excitation torque induced by the friction elements during engagement. Results confirmed that the system fluctuations during the engagement occur due to the excitation induced by the friction elements. The sys tem instability referred to the shunt phenomena could occur when increasing the gradient of friction coefficient and/or decreasing the system damping. High value of system damping tends to discourage self excitation vibration and increasing system stability.
The system response is now predictable with change of the system parameters which opens up the opportunity in future to control the vibration level
6. REFERENCES
- E. M. Rabeih, “Torsional Vibration Analysis of Automotive Drivelines,” Ph.D. Thesis, Leeds University, Leeds, 1997.
- J. Persson, “Integrated Powertrain Control—A Literature Survey on Longitudinal Vibrations, Drivability Aspects and Future Challenges,” MSc. Thesis, Control and Automation Laboratory, Department of Signal and Systems, Chalmers University, Chalmers, 2004.
- L. Coudrec, J. Callenaere, J. Der Hagopian and G. Ferraris, “Vehicle Driveline Dynamics Behavior: Experimentation and Simulation,” Journal of Sound and Vibration, Vol. 218, 1998, pp. 133-157. doi:10.1006/jsvi.1998.1808
- N. Zhang, D. Liu, J. Jeyakumaran and L. Villanueva, “Modeling of Dynamic Characteristics of an Automatic Transmission during Shift Changes,” Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, Vol. 216, No. 4, 2002, pp. 331-341.
- W. Han and S. Yi, “A Study of Shift Control Using the Clutch Pressure Pattern in Automatic Transmission,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 217, No. 4, 2003, pp. 289-298. doi:10.1243/09544070360613246
- A. Haj-Fraj and F. Pfeiffer, “Optimal Control of Gear Shift Operations in Automatic Transmissions,” Journal of The Franklin Institute, Vol. 338, No. 2-3, 2001, pp. 371- 390. doi:10.1016/S0016-0032(00)00091-0
- H. Mikael, “Apparatus for Measurement of Engagement Characteristics of a Wet Clutch,” Wear, Vol. 213, No. 1, 1997, pp. 140-147. doi:10.1016/S0043-1648(97)00202-0
- E. O. A. Abd Elmaksoud, E. M. Rabeih, N. A. Abdel-halim and S. M. El Demerdash, “Investigation of the Torsional Vibration of Automatic Transmission System with Simple Planetary Gear Set during the Engagement,” Engineering Research Journal, Vol. 127, 2010, pp. AT1- AT14
- J.-M. Seo and S.-J. Yi, “Design of an Automatic Transmission System Having an Arbitrary Power Flow Using the Automatic Power Flow Generation Algorithm,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 219, No. 9, 2005, pp. 1085-1097. doi:10.1243/095440705X34766
- S. Hwang, J. Chen, L. Liu and C. Ling, “Modeling and Simulation of a Powertrain Vehicle System with Automatic Transmission,” International Journal of Vehicle Design, Vol. 23, No. 1-2, 2000, pp. 145-160. doi:10.1504/IJVD.2000.001888
- H. Heisler, “Advanced Vehicle Technology,” 2nd Edition, Butterworth-Heinemann, Oxford, 2002.


