Engineering
Vol. 3 No. 3 (2011) , Article ID: 4144 , 4 pages DOI:10.4236/eng.2011.33027
Analysis of the Spectral Resolution of a TeO2 Based Noncollinear Acousto-Optic Tunable Filter*
Key Laboratory of OptoElectronic Science and Technology for Medicine of Ministry of Education, Fujian Provincial Key Laboratory for Photonics Technology, School of Physics and OptoElectronics Technology, Fujian Normal University, Fuzhou, China
E-mail: cgzhang@fjnu.edu.cn
Received December 23, 2010; revised January 11, 2011; accepted January 14, 2011
Keywords: Spectral Resolution, AOTF, Spectral Bandwidth, TeO2
ABSTRACT
The spectral resolution is a main index of evaluating the performance of the designed acousto-optic tunable filter (AOTF). In this letter, an accurate expression of the spectral resolution is presented by considering both the birefringence and the rotatory property of TeO2 crystal. The deduced expression is significant in improving the accuracy of the design of an AOTF and pushing the development of the high-performance AOTF.
1. Introduction
AOTF has been used in a wide range of applications, such as laser wavelength tuning, spectral analysis, spectral imaging [1-3], and etc. TeO2 is a kind of A-O crystal with many applications in the large angular aperture noncollinear AOTF. Light diffraction by acoustic wave propagating in the A-O crystal is the foundation of the operation of an AOTF. During the A-O interaction, the filtered optical wavelength of AOTF is changed with the frequency of the acoustic wave, and the diffracted light has a narrow spectral band centered on a chosen wavelength. The acoustic wave can be generated when a radio frequency signal (rf) is applied to a piezoelectric transducer bonded on the birefringent material, so a change in the applied rf produces a variation in the acoustic wave frequency. Previous studies had confirmed that considering the birefringence of the interaction material and its rotatory property was an effective method of increasing the accuracy of the design obviously [4,5]. The spectral resolution is a key index of evaluating the performance of an AOTF for the actual applications. However, the previous expression of the spectral resolution which had been widely used is inaccurate for the neglect of the rotatory property [4-7]. Thus, in this letter, we give an exact expression of the spectral resolution in order to keep up the higher demand for the accurate evaluation of the performance of AOTF.
2. Theory of Acousto-Optic Interaction in AOTF
A design of noncollinear AOTF with TeO2 is based on A-O interaction in [1-10] plane. Both the birefringence and the rotatory property of the interaction materials should be considered in the design of AOTF, in order to ensure the accuracy of the design of AOTF. Two eigen wave modes can propagate in TeO2 crystal. They are right-handed elliptical polarized mode and left-handed elliptical polarized one, and the direction of the ellipse’ long axes on these two modes are parallel with the main plane and perpendicular to the main plane, respectively. If the incident beam is right-handed elliptical polarized, the diffracted one will be left-handed elliptical polarized. Accordingly, the diffracted beam will be left-handed elliptical polarized when the incident one is right-handed elliptical polarized. The wave vector diagram of A-O interaction is drawn in Figure 1. ki, kd and Ka indicate the incident optical wave vector, the diffracted optical wave vector and the acoustic wave vector, respectively. ki + Ka = kd, and the direction of the acoustic wave propagation satisfies the parallel tangents momentummatching condition. In the following discussions of this letter, the incident beam is assumed to be right-handed elliptical polarized, the diffracted one is left-handed elliptical polarized.
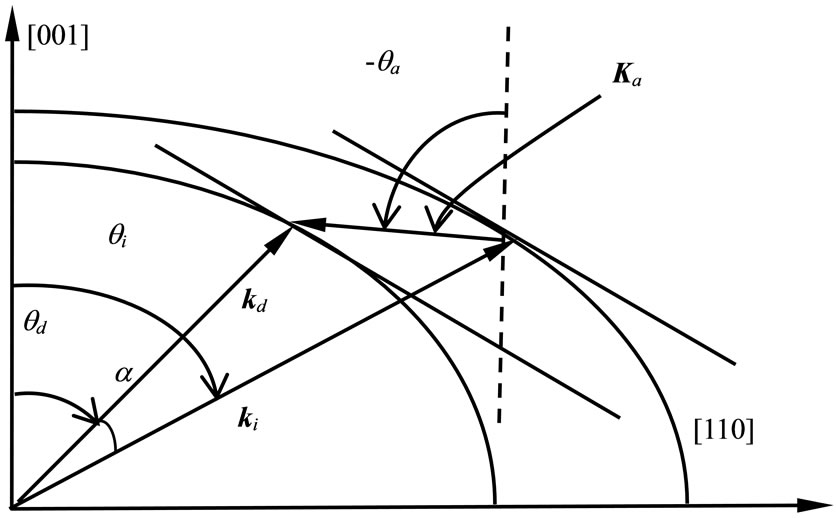
Figure 1. The wave vector diagram of a noncollinear AOTF. [001] axis is the optic axis.
The refractive indices of the incident beam (ni) and the diffracted beam (nd) can be expressed as,
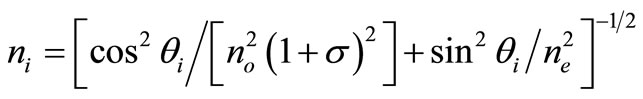 (1)
(1)
 (2)
(2)
where θi and θd are the polar angle for the incident and the diffracted beams. σ is relevant with specific rotation ρ by σ = λρ/2πno. σ and ρ have wavelength dependence [4]. no and ne are the ordinary and extraordinary refractive indices in the direction perpendicularly to the optical axis, respectively. They are the function of the optical wavelength λ0 in free space [8],
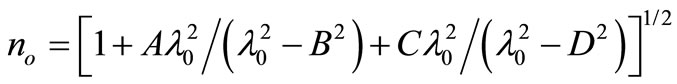 (3)
(3)
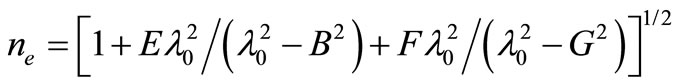 (4)
(4)
where A = 2.5844, B = 0.1342, C = 1.1557, D = 0.2638, E = 2.8525, F = 1.5141 and G = 0.2631. The unit of λ0 is micron in (3) and (4). Under the momentum-matching condition, the wave-vector propagation polar angles are,
 (5)
(5)
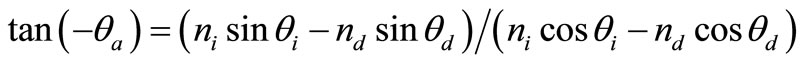 (6)
(6)
θa is the acoustic wave angle. The relationship between θa and θi is
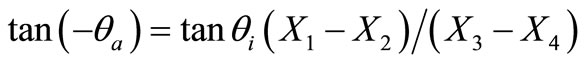 (7)
(7)
With,
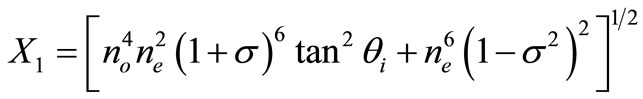
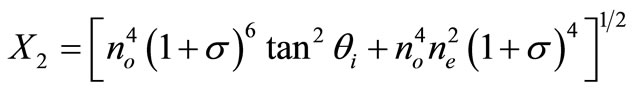

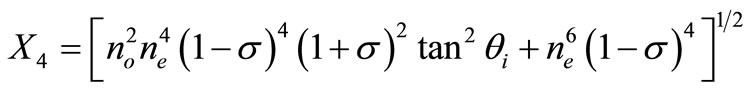
3. Analysis of Spectral Resolution of AOTF
The optical bandpass characteristics of AOTF are determined by the momentum mismatch caused by the deviation of wavelength from the exact momentummatching condition. If the rotatory property is out of consideration, the common equation of the spectral bandwidth was 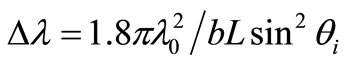 [8-10]. Here, the dispersion constant b is expressed as:
[8-10]. Here, the dispersion constant b is expressed as:
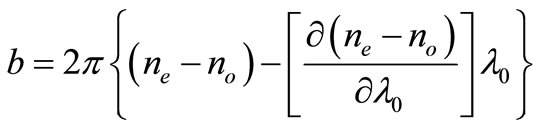 (8)
(8)
In this section, an exact expression of the spectral bandwidth  will be deduced with considering both the birefringence and the rotatory property of TeO2.
will be deduced with considering both the birefringence and the rotatory property of TeO2.
Commonly, the diffraction efficiency  is expressed as,
is expressed as,
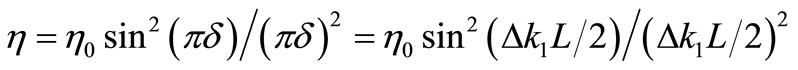 (9)
(9)
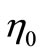 is the peak diffraction efficiency.
is the peak diffraction efficiency.  is relevant with the power of the rf signal and the geometry of A-O crystal.
is relevant with the power of the rf signal and the geometry of A-O crystal. 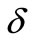 is the mismatch factor.
is the mismatch factor.  indicates the momentum mismatch. Generally, the input surface of the AOTF is manufactured perpendicular to the incident light. So we can give the expression of the momentum mismatch
indicates the momentum mismatch. Generally, the input surface of the AOTF is manufactured perpendicular to the incident light. So we can give the expression of the momentum mismatch 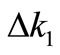 from Figure 1,
from Figure 1,
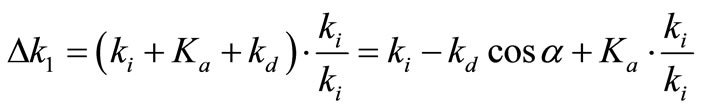 (10)
(10)
Here cos α = 1 when α is small enough. We define 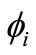 and
and 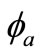 as the azimuth angle of the incident optical wave vector and the acoustic wave vector, respectively. The direction cosine of Ka and ki can be derived by (
as the azimuth angle of the incident optical wave vector and the acoustic wave vector, respectively. The direction cosine of Ka and ki can be derived by (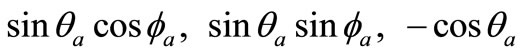 ) and (
) and (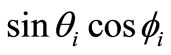 ,
,  ,
,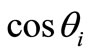 ) respectively. Thus,
) respectively. Thus,
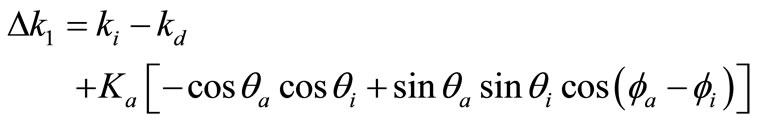 (11)
(11)
For the large angular aperture AOTF, it requires that the 1st-order derivative of  with respect to angular deviations
with respect to angular deviations 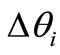 and
and 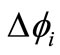 be zero. From (11),
be zero. From (11), 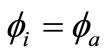 is satisfied. We assume Ka/kd = a. Then,
is satisfied. We assume Ka/kd = a. Then,
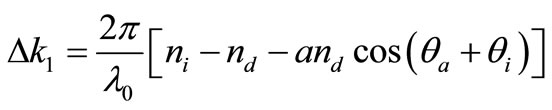 (12)
(12)
The Taylor series expansion of momentum mismatch
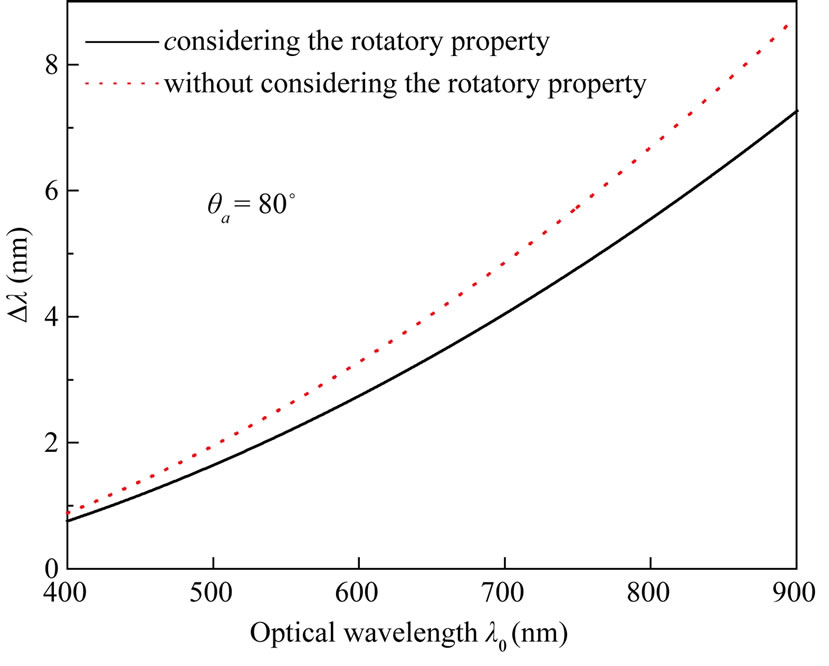
Figure 2. The spectral bandwidth versus the optical wavelength. The acoustic angle is fixed at 80˚ and L = 4 mm.
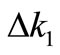 near
near 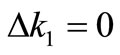 is, θ
is, θ
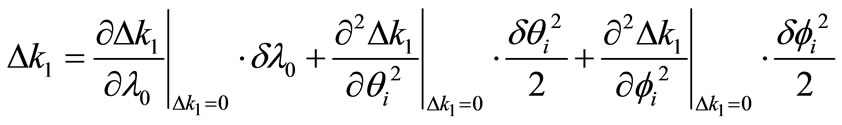 (13)
(13)
It can be got from (12) that,
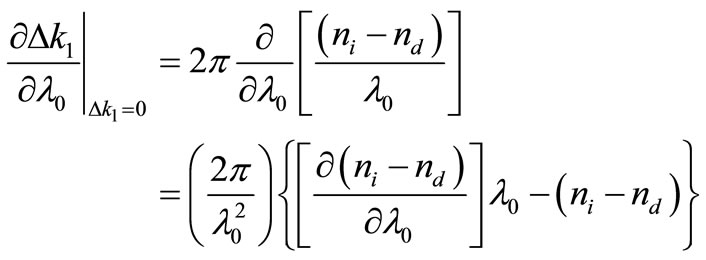 (14)
(14)
We define b′ as the dispersive constant,
 (15)
(15)
b′ can be calculated by the differentiation of (1)-(4). Then,
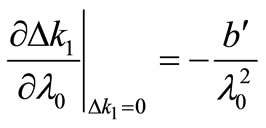 (16)
(16)
The condition of half-peak diffraction efficiency (η = η0/2) occurs when 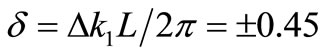 from (9). Thus, the full spectral bandwidth can be expressed as,
from (9). Thus, the full spectral bandwidth can be expressed as,
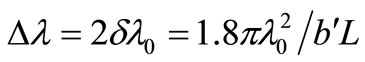 (17)
(17)
Figure 2 gives the comparison of the optical wavelength dependence of the spectral bandwidth 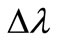 between our exact expression with that commonly used one.
between our exact expression with that commonly used one.
It shows that the difference between our exact expression and previous expression is obvious, which indicates the necessity of this accurate expression of the spectral resolution of an AOTF in this letter.
4. Conclusions
For a designed AOTF, the spectral resolution is a main index to be considered in the evaluation of its performance. In this letter, we have deduced an accurate expression to describe the spectral bandwidth by considering both the birefringence and the rotatory property of the interaction materials. By comparison, we have found that, the difference between our expression of the spectral bandwidth and previously used expression is obvious. Our study can be significant for the design of modern AOTF with excellent performance.
5. REFERENCES
- N. Gupta and R. Dahmani, “Acousto-Optic Tunable Filter Based Visible-to near-Infraed Spectropolarimetric Imager,” Optical Engineering, Vol. 41, No. 5, 2002, pp. 1033-1038. doi:10.1117/1.1467936
- N. Gupta and V. B. Voloshinov, “Development and Characterization of Two-transducer Imaging Acousto-Optic Tunable Filters with Extended Tuning Range,” Applied Optics, Vol. 46, No. 7, 2007, pp. 1081-1088. doi:10.1364/AO.46.001081
- V. B. Voloshinov, et al., “Improvement in Performance of a TeO2 Acousto-Optic Imaging Spectrometer,” Journal of Optics A, Vol. 9, No. 4, 2007, pp. 341-347.
- C. G. Zhang, Z. H. Zhang, Y. Yang and H. Wang, “Design and Analysis of a Noncollinear Acousto-Optic Tunable Filter,” Optics Letters, Vol. 32, No. 16, 2007, pp. 2417-2419. doi:10.1364/OL.32.002417
- C. G. Zhang, Z. H. Zhang, H. Wang and Y. Yang, “Analysis of the Optimum Optical Incident Angle for an Imaging Acousto-Optic Tunable Filter,” Optics Express, Vol. 15, No. 19, 2007, pp. 11883-11888. doi:10.1364/OE.15.011883
- I. C. Chang, “Noncollinear Acousto-Optic Filter with Large Angular Aperture,” Applied Physics Letters, Vol. 25, No. 7, 1974, pp. 370-372. doi:10.1063/1.1655512
- P. A. Gass and J. R. Sambles, “Accurate Design of Noncollinear Acousto-Optic Tunable Filter,” Optics Letters, Vol. 16, No. 6, 1991, pp. 429-431. doi:10.1364/OL.16.000429
- D. R. Suhre and J. G. Throdore, “White-Light Imaging by Use of a Multiple Passband Acousto-Optic Tunable Filter,” Applied Optics, Vol. 35, No. 22, 1996, pp. 4494- 4501. doi:10.1364/AO.35.004494
- I. C. Chang, “Analysis of the Noncollinear Acousto-Optic Filter,” Electronics Letters, Vol. 11, No. 25, 1975, pp. 617- 618. doi:10.1049/el:19750470
- I. C. Chang and P. Katzka, “Enhancement of AcoustoOptic Filter Resolution using Birefringence Dispersion in CdS,” Optics Letters, Vol. 7, No. 11, 1982, pp. 535-536. doi:10.1364/OL.7.000535
NOTES
*Natural Science Foundation of Fujian Province of China (2010J05131 and 2010J05129).

