Engineering
Vol. 3 No. 2 (2011) , Article ID: 4285 , 4 pages DOI:10.4236/eng.2011.32016
Modeling and Adaptive Self-Tuning MVC Control of PAM Manipulator Using Online Observer Optimized with Modified Genetic Algorithm
1Faculty of Electrical and Electronic Engineering, HCM City University of Technology,
Ho Chi Minh City, Viet Nam
2DCSELAB, HCM City University of Technology, Ho Chi Minh City, Viet Nam
Email: hphanh@hcmut.edu.vn, thanhnam@vnuhcm.edu.vn
Received August 15, 2010; revised September 3, 2010; accepted January 4, 2011
Keywords: Modified Genetic Algorithm (MGA), Online System Identification, ARX Model, Pneumatic Artificial Muscle (PAM), PAM Manipulator, Minimum Variance Controller (MVC)
ABSTRACT
In this paper, the application of modified genetic algorithms (MGA) in the optimization of the ARX Model-based observer of the Pneumatic Artificial Muscle (PAM) manipulator is investigated. The new MGA algorithm is proposed from the genetic algorithm with important additional strategies, and consequently yields a faster convergence and a more accurate search. Firstly, MGA-based identification method is used to identify the parameters of the nonlinear PAM manipulator described by an ARX model in the presence of white noise and this result will be validated by MGA and compared with the simple genetic algorithm (GA) and LMS (Least mean-squares) method. Secondly, the intrinsic features of the hysteresis as well as other nonlinear disturbances existing intuitively in the PAM system are estimated online by a Modified Recursive Least Square (MRLS) method in identification experiment. Finally, a highly efficient self-tuning control algorithm Minimum Variance Control (MVC) is taken for tracking the joint angle position trajectory of this PAM manipulator. Experiment results are included to demonstrate the excellent performance of the MGA algorithm in the NARX model-based MVC control system of the PAM system. These results can be applied to model, identify and control other highly nonlinear systems as well.
1. Introduction
Nowadays, the new type of pneumatic actuator, McKibben artificial muscle or pneumatic artificial muscle (PAM), possessed all the advantages of traditional pneumatic actuators (i.e., light weight, low cost) without the main drawback (i.e., low power-to-weight ratio) is becoming increasingly popular. PAM actuators have the highest power/weight and power/volume ratios as well in comparison with other actuators [1,2](2005). Many potential applications involve some type of exo-skeletal or link segment configuration that attaches to existing anatomical body-segments [3-6]. Research into the control and the physical and modeling properties of PAM has been undertaken at the INSA (Toulouse, France) [7], the Bio-Robotics Lab at the University of Washington, Seattle, [8], Human Sensory Feedback (HSF) Laboratory at Wright Patterson Air Force Base [9], and Fluid Power and Machine Intelligence Laboratory (FPMI) at Ulsan University [10-12] and so on.
This paper addresses the modeling, identification and control of a PAM manipulator actuated by a group of antagonistic PAM pair. Due to their highly nonlinear and time-varying parameter nature, PAM manipulator control presents a challenging nonlinear control problem that has been approached via many methodologies. Related literature has appeared lots of ways for modeling and control the PAM actuator. In [13], a direct continuous-time adaptive control technique is applied to control joint angle in a single-joint robot arm. The simulation considers PAM individually in both bicep and tricep positions. In [14], an indirect discrete adaptive controller is used to control an antagonistic PAM pair actuating an actual ro-botic arm. In [15], an antagonistic PAM pair actuates a leg-like swinging pendulum in the lab. The PAM is actuated in periodic fashion to mimic walking movements, and the action is controlled by a digital pole-placement controller. In [16], PAM is used in the actuation of a hand-like manipulator in the lab. A linear discrete model of the process is identified offline via least mean squares (LMS), and a discrete pole-placement controller with in-tegral action is designed. In [17], a five-link robot in the laboratory is controlled by a neural network using back propagation to learn the correct control over a period of time. In [18], a gain scheduling controller is designed for a single PAM hanging vertically in the lab actuating a mass. Both force as well as position control are considered. In [19], a fuzzy model reference learning controller is designed for a single PAM hanging vertically actuating a mass in the lab. Tracking results are obtained, and these are shown to agree well with simulated results. In [20], a fuzzy P + ID controller is designed for the same previous system. The novel feature is a new method of identifying fuzzy systems from experimental data using evolutionary techniques. The experimental results are shown to be superior to those in [19], i.e., tracking error is less while using less control effort. In [21], a back-stepping controller using fuzzy techniques to determine valve status is designed for a simulation of a PAM hanging vertically in the lab. In [22], sliding-mode control is applied to a three degree-of-freedom (DOF) PAM-actuated anthropomorphic manipulator in the lab. Sliding mode control is also used in [23-24]. In [25], Hinf method is used for PAM control. Recently, in [11], it applied thoroughly Modified GA (MGA) for optimizing parameters of pseudo-linear ARX model of the PAM manipulator. In [12], authors identified successfully PAM manipulator based on nonlinear fuzzy NARX mo-del. All these results prove that up to now, it is still lack of a simple and quite efficient model for the PAM manipulator which will be utilized efficiently in adaptive & self-tuning control such highly nonlinear system like the PAM manipulator system.
The contributions of this paper include firstly modeling, identifying and controlling of the PAM manipulator using novel proposed MGA-based optimized ARX mo-del; secondly formulating a simple but highly efficient novel Modified RLS (MRLS) observer so that it is suitable for online parameter self-tuning; finally applying MVC controller based on MRLS observer for position control the highly nonlinear PAM manipulator and obtaining from experiment out-performing results.
The rest of this paper is arranged as follows. Section 2 introduces modified genetic algorithm (MGA) used in PAM manipulator modeling and identification. Section 3 presents and analyses the results of MGA-based PAM manipulator identification process. Section 4 introduces the novel proposed Modified Recursive Least Square (MRLS) observer for online updating parameters of PAM manipulator system. Section 5 introduces the proposed MVC control algorithm based on online updating ARX model parameter using MRLS observer to adaptive control the PAM manipulator. Section 6 presents the hardware configuration of the PAM manipulator system used in process of modeling, identification and control. Section 7 presents experiment results of the joint angle trajectory tracking of the PAM manipulator using MVC controller. Finally, Section 8 contains conclusion.
2. Modified Genetic Algorithm (MGA) for Optimizing the ARX Model Parameters
2.1. Introduction
A general nonlinear model is considered:
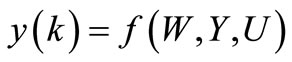 (1)
(1)
with f( ) is a nonlinear function such that (1) is stable in the sense of Lyapunov; 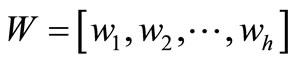 is a set of h fixed parameters;
is a set of h fixed parameters; 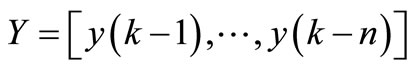 is a set of n autoregressive output terms and
is a set of n autoregressive output terms and
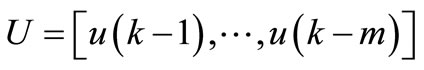 is a set of m past input values.
is a set of m past input values.
In case the structure of f( ) assumed to be known, (1) can be estimated as
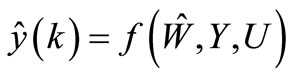 (2)
(2)
with 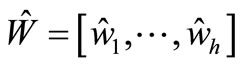 is a set of h parameters estimated,
is a set of h parameters estimated, 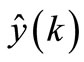 is estimated output and U,Y is defined as above.
is estimated output and U,Y is defined as above.
In order to apply Modified Genetic Algorithm (MGA), each estimated parameter 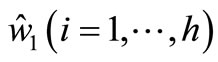 will be enco-ded as a binary string called a gene. All genes are cascaded for forming a longer string
will be enco-ded as a binary string called a gene. All genes are cascaded for forming a longer string 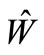 called a chromosome. This novel identification strategy is to apply MGA to search for the best chromosome
called a chromosome. This novel identification strategy is to apply MGA to search for the best chromosome 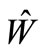 so that
so that
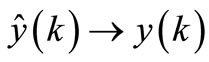 from the testing input-output data range. Each generation will explore a collection of N chromosomes of estimated parameters.
from the testing input-output data range. Each generation will explore a collection of N chromosomes of estimated parameters.
Consider fitness value associated with the jth chromosome in a population which is defined as
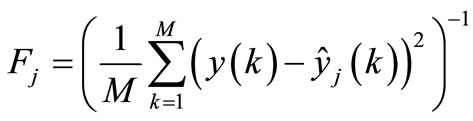 (3)
(3)
in which k is the discrete time index in identification process; M is the window size through which errors will be accumulated and 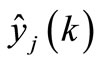 is the estimated kth output belong to the jth chromosome of estimated parameters. In each generation, MGA will search for the maximum fitness value over the entire space of parameters. Experimentally, a larger M value gets, a slower down execution of the MGA becomes. Unfortunately, a small M va-lue makes the estimation tend to oscillate. Consequently, a trade-off should be considered for choosing an available M value.
is the estimated kth output belong to the jth chromosome of estimated parameters. In each generation, MGA will search for the maximum fitness value over the entire space of parameters. Experimentally, a larger M value gets, a slower down execution of the MGA becomes. Unfortunately, a small M va-lue makes the estimation tend to oscillate. Consequently, a trade-off should be considered for choosing an available M value.
2.2. MGA Algorithm Procedure
It needs to tune following parameters before running the MGA algorithm:
D: number of chromosomes chosen for mating as parents
N: number of chromosomes in each generation
Lt: number of generations tolerated for no improvement on the value of the fitness before MGA terminated
Le: number of generations tolerated for no improvement on the value of the fitness before the operator extinction is applied. It need to pay attention that .
.
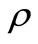 : portion of chosen parents permitted to be survived into the next generation
: portion of chosen parents permitted to be survived into the next generation
q: percentage of chromosomes are survived according to their fitness values in the extinction strategy
The steps of MGA-based model identification procedure are summarized as follows:
Implement tuning parameters described as above. Encode estimated parameters into genes and chromosomes as a string of binary digits. Considering that parameters lie in several bounded region hk
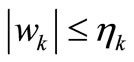 for
for . (4)
. (4)
The length of chromosome needed to encode wk is ba-sed on hk and the desired accuracy dk. Set 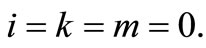
Generate randomly the initial generation of N chromosomes. Set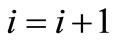 .
.
Decode the chromosomes then calculate the fitness value for every chromosome of population in the generation. Consider 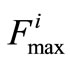 the maximum fitness value in the ith generation.
the maximum fitness value in the ith generation.
Apply the Elitist strategies to guarantee the survival of the best chromosome in each generation. Then apply the G-bit strategy to this chromosome for improving the efficiency of MGA in local search.
1) Reproduction:
In this paper, reproduction is set as a linear search through roulette wheel values weighted proportional to the fitness value of the individual chromosome. Each chromosome is reproduced with the probability of
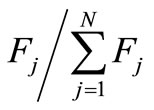 with j being the index of the chromosome
with j being the index of the chromosome 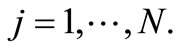 Furthermore, in order to prevent some str-ings possess relatively high fitness values would lead to premature parameter convergence, in practice, linear fit-ness scaling will be applied.
Furthermore, in order to prevent some str-ings possess relatively high fitness values would lead to premature parameter convergence, in practice, linear fit-ness scaling will be applied.
2) Crossover:
Choose D chromosomes possessing maximum fitness value among N chromosomes of the present gene pool for mating and then some of them, called 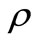 best chromosomes, are allowed to survive into the next generation. The process of mating D parents with the crossover rate pc will generate
best chromosomes, are allowed to survive into the next generation. The process of mating D parents with the crossover rate pc will generate 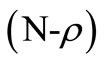 children. Pay attention that, in the identification process, it is focused the mating on parameter level rather than on chromosome level.
children. Pay attention that, in the identification process, it is focused the mating on parameter level rather than on chromosome level.
3) Mutation:
Mutate a bit of string (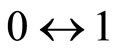 ) with the mutation rate Pm.
) with the mutation rate Pm.
Compare if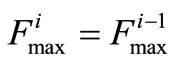 , then
, then 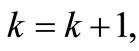
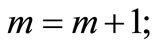 otherwise,
otherwise, 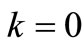 and
and 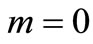 .
.
Compare if 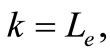 then apply the extinction strategy with
then apply the extinction strategy with 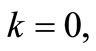
Compare if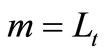 , then terminate the MGA algorithm; otherwise go to Step 3.
, then terminate the MGA algorithm; otherwise go to Step 3.
The flow chart of proposed MGA-based PAM manipulator Identification process is given in Figure 1.
3. Results of MGA-based PAM Manipulator Identification Method
MGA-based 2-axes PAM manipulator Identification re-sults are presented by comparing between Least Mean Square (LMS) and Modified Genetic Algorithm (MGA) methods for the PAM manipulator identification.
Parameter estimation process can be viewed like a searching problem for suitable values in the parameter space. The purpose aim to minimize the error function relating the simulated output and the measurement from a real plant with both get the same excitation signal input. From related literature, it has been applied a few me-thods available for solving such optimization problems. With identification process in which the performance surface isn’t complicated, conventional linear or nonlinear optimization may be suitable. However, the PAM manipulator possesses performance surface being a very nonlinear and noisy disturbances of intrinsic control. Conventional methods may not work well.
With a typical parameter estimation process, parameters of the time delay and the order of the model are assumed to be known. Thus estimated parameters are the other coefficients in the model. In this paper, by using MGA not only these coefficients but also time delay, where difficulties arise, are estimated.
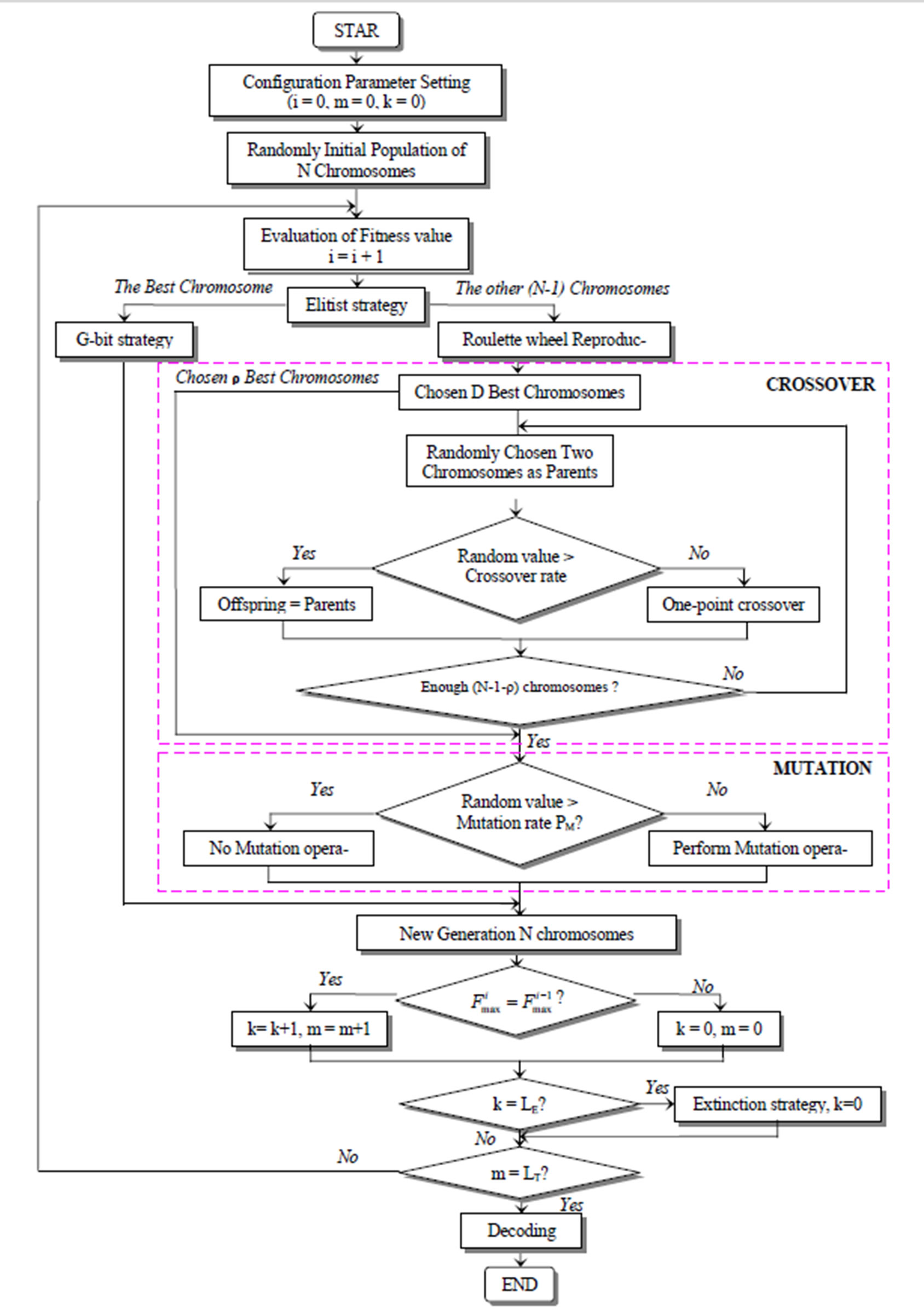
Figure 1. Flow chart of MGA-based optimal Identification Process.
Considering an ARX model with noisy input which can be described as
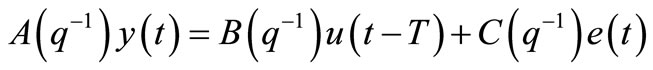 (5)
(5)
with
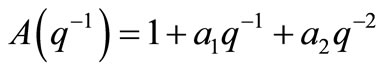
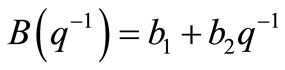
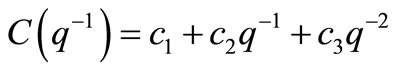
e(t) is the white noise sequence with zero mean and unit variance; u(t) and y(t) are input and output of system respectively; q is the forward shift operator and T is the time delay.
The purpose here is to compare between MGA with simple GA (GA) and LMS methods for identifying a1, a 2, b1 and b2 parameters in present of the noise. The excitation input u(t) to be used is chosen as pseudo random binary sequence (PRBS). Figure 2 presents the PRBS input applied to the real PAM manipulator and the corresponding output.
The fitness function calculated in this case is given as
 (6)
(6)
with e(k) represents the error between the actual PAM manipulator joint angle output and estimated joint angle output values derived from a1, a 2, b1 and b2 parameters of PAM manipulator ARX model.
For MGA-based estimated parameter optimization, the tuning parameters of the MGA are implemented as follows:
a) Number of chromosomes in each generation N = 100;
b) Number of chromosomes chosen as parents for mating D = 25;
c) Number of generations tolerated for no improvement on the value of the fitness value before the MGA is terminated Lt = 50;
d) Number of generations tolerated for no improve-ment on the value of the fitness value before the extinction strategy is applied Le = 5;
e) String length of each parameter: 12 bits (resolution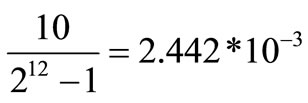 )
)
f) String length of time delay: 3 bits (resolution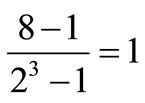 )
)
g) Crossover probability Pc = 0.85
h) Mutation probability Pm = 0.05
i) Search range of the parameters : [–2, 2]
j) The portion of chosen parents allowed to survive into next generation r = 25.
k) The best q% of chromosomes are survived according to their fitness values in the extinction strategy q% = 15%.
In the optimization process, LMS, GA as well as MGA algorithms are programmed in M-file running off-line in MATLAB. The conventional GA is tested for 100 generations, equal to MGA generations. The population of GA and MGA are 300 and 50 respectively. Initial po-pulations are created randomly, i.e., no a priori knowledge is needed. Both fitness values converge toward the global optimum, as shown in Figure 3.
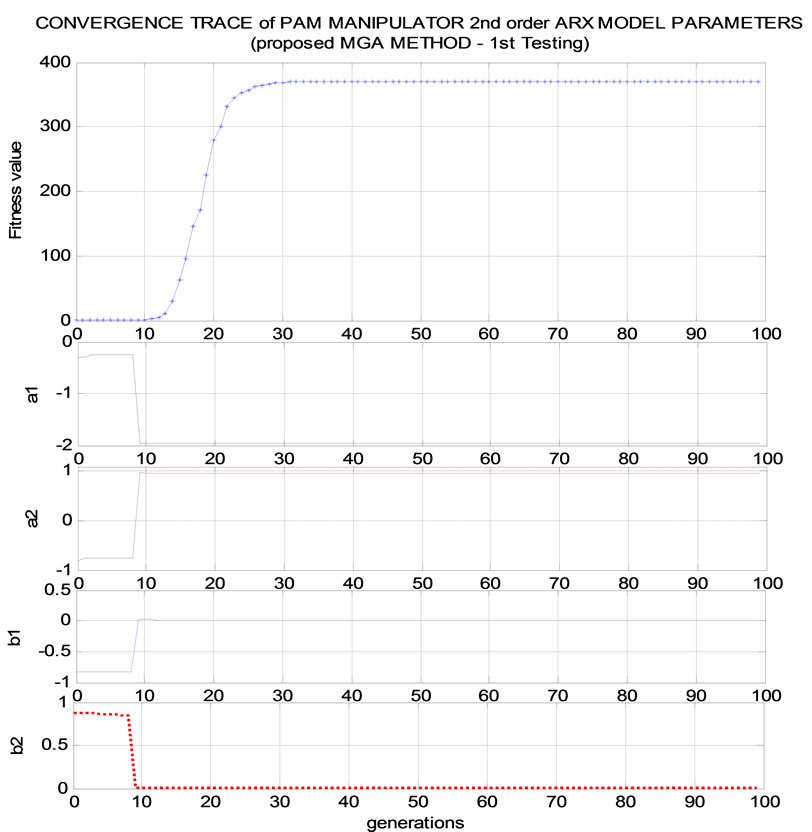
The convergence plot of the identified parameters by the MGA is shown in Figure 4(a) and Figure 4(b).
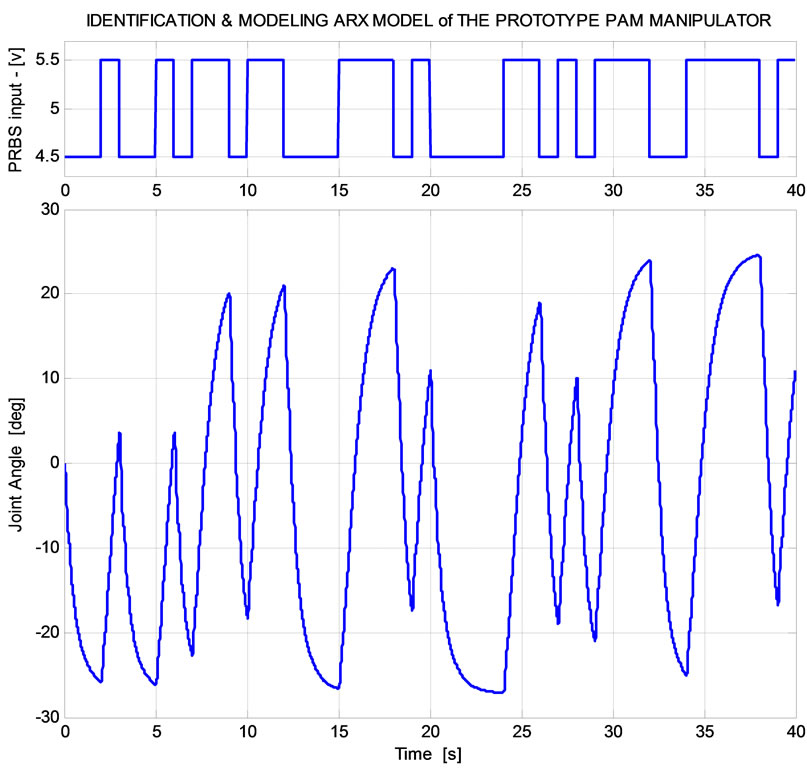
Figure 2. Input signal and output response of the PAM manipulator.
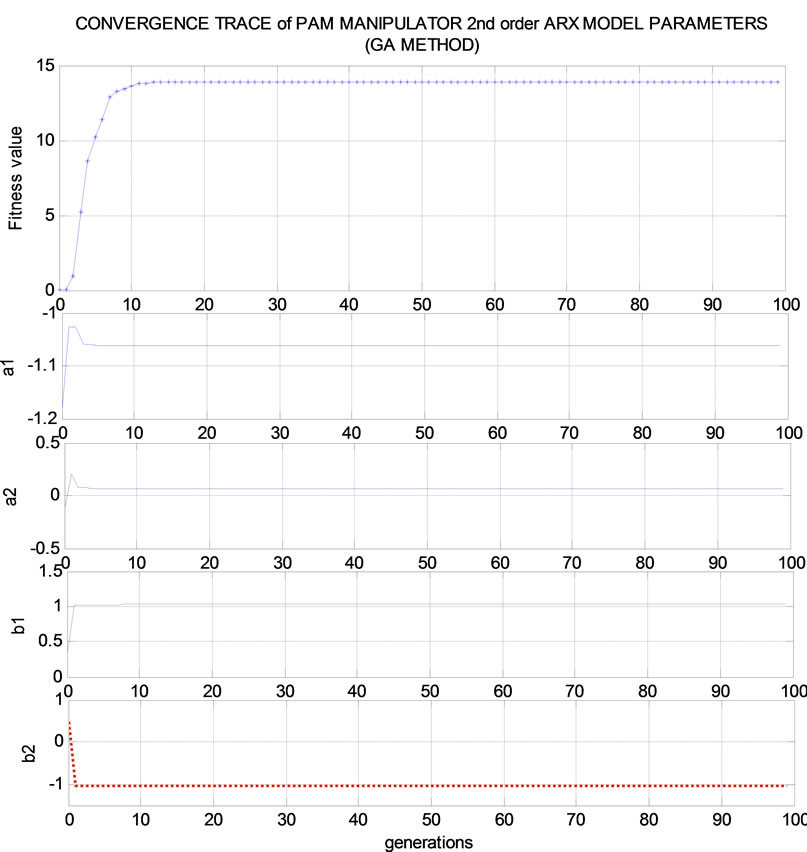
Figure 3. Convergence trace of the fitness value and the identified parameters (GA method).
From these figures, it can be seen that, even with the present of noise, the identification parameter value converges rapidly from a random set of parameters with best obtained fitness value. These results prove the superior of MGA identification method over classic GA method. Fitness value from MGA method is more twice than fitness value obtained from GA. The optimized identified parameters obtained from GA and MGA as well at the
 (a)
(a)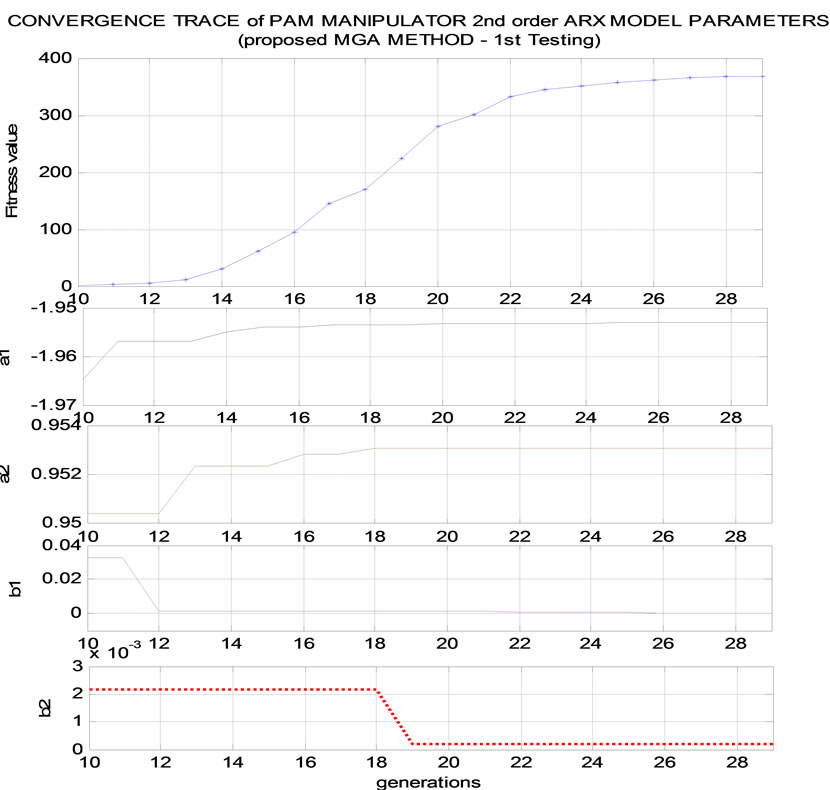 (b)
(b)
Figure 4. (a) Convergence trace of PAM manipulator 2nd order ARX model parameters and fitness value (MGA algorithm); (b) Convergence trace of the 2-axes PAM manipulator 2nd order ARX model (MGA algorithm)-zoom out the 10th to 29th generations.
end of 100th generation are tabulated in Table 1.
For comparison, a conventional least mean square (LMS) identification technique is used to identify the pa-rameters of A(q-1) and B(q-1). The obtained parameters from LMS identification technique are shown below: a1 = –1.9115; a2 = 0.91264; b1 = –0.002212; b2 = 0.05933. In comparison with the conventional LMS as well as GA methods, the identified ARX model obtained from the MGA is shown to outperform with high accuracy. Figure 5 presents the output of the MGA and LMS identified models against the actual output response without the present of the white noise when the same input PRBS data set is used.
Figure 6 shows the frequency response between them. This figure also demonstrates the excellent result of the identified model obtained from MGA in comparison with GA and LMS identification methods.
From the results presented in previous figures, it proves conclusion that the MGA-based system identification has obtained an unbiased estimation not only of the PAM manipulator but also of the other dynamic nonlinear system possessed noise input.
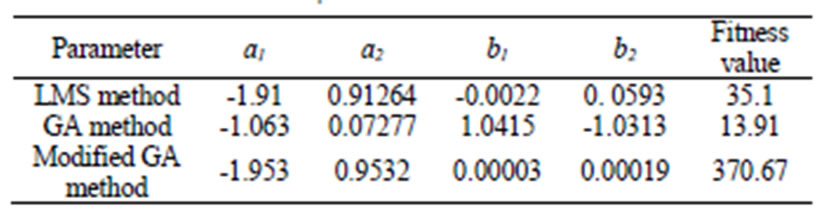
Table 1. PAM manipulator ARX model parameters (LMS, GA and MGA method).
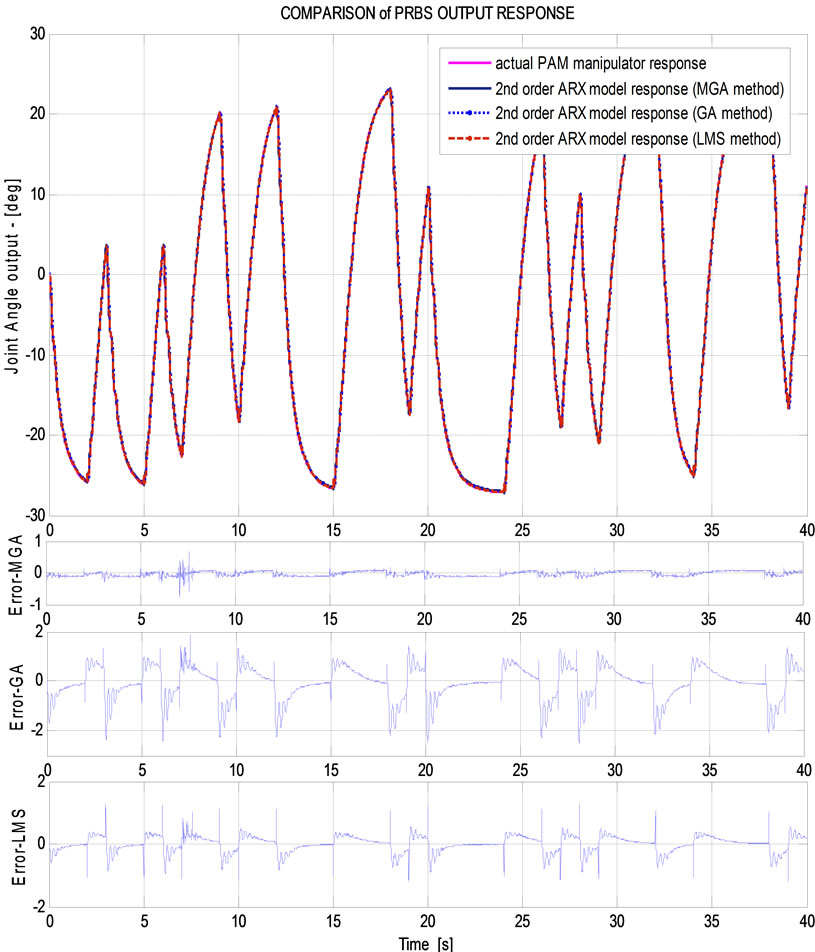
Figure 5. Output of MGA and LMS identification methods against actual response.
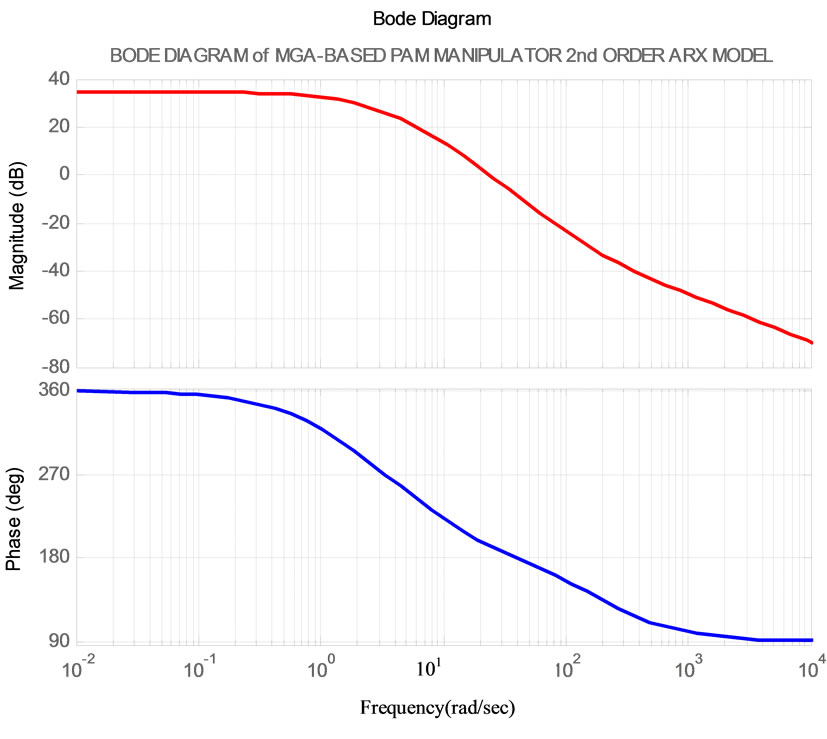
Figure 6. Frequency response of MGA identification model.
4. Modified Recursive Least Square (MRLS) Observer
This section describes MRLS method used in the paper for the online process identification. The novel proposed Modified RLS (MRLS) method is improved from the conventional Least squares method (LSM). This method can be used for the discrete online identification of pro-cesses that are described by the following transfer function.
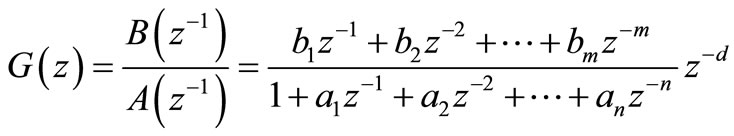 (7)
(7)
The estimated output of the process in step k (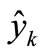 ) is computed on base of the previous process inputs u and outputs y according to the equation:
) is computed on base of the previous process inputs u and outputs y according to the equation:
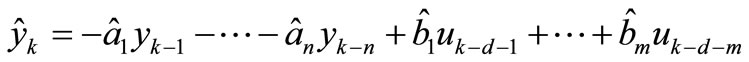 (8)
(8)
where 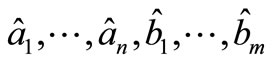 are the current estimations of process parameters. This equation can be also written in vector form, which is more suitable for further work - see equation:
are the current estimations of process parameters. This equation can be also written in vector form, which is more suitable for further work - see equation:
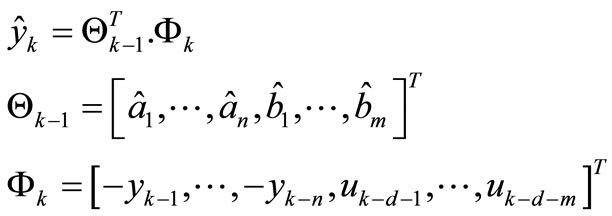 (9)
(9)
The vector 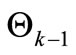 contains the process parameter estimations computed in previous step and the vector
contains the process parameter estimations computed in previous step and the vector 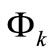 contains output and input values for computation of cur-rent output yk. This vectors record is used in description of individual identification method in further sections. Least square method (LSM) is based on minimization of the sum of prediction errors squares:
contains output and input values for computation of cur-rent output yk. This vectors record is used in description of individual identification method in further sections. Least square method (LSM) is based on minimization of the sum of prediction errors squares:
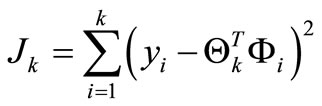 (10)
(10)
where yi is process output in ith step and the product represents predicted process output. Solving this equation leads to the recursive version of least square method (LSM) where vector of parameters estimations is updated in each step according to equation:
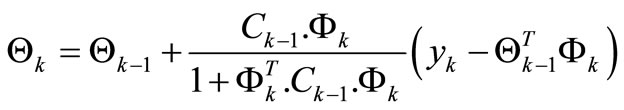 (11)
(11)
The covariance matrix C is then updated in each step as defined by the equation:
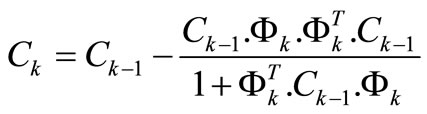 (12)
(12)
Initial value of matrix C determines influence of initial parameter estimations to the identification process.
The MRLS method can be further improved by adaptive directional forgetting which changes forge-tting co-efficient with respect to changes of input and output sig-nal. Process parameters are updated using recursive equation:
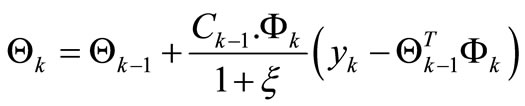 (13)
(13)
where
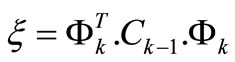 (14)
(14)
Matrix C is updated in each step according to equation:
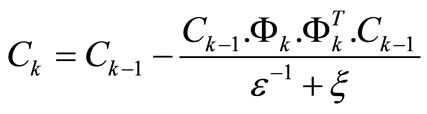 (15)
(15)
where
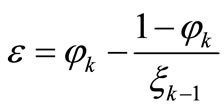 (16)
(16)
Forgetting coefficient 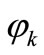 is updated as follows:
is updated as follows:
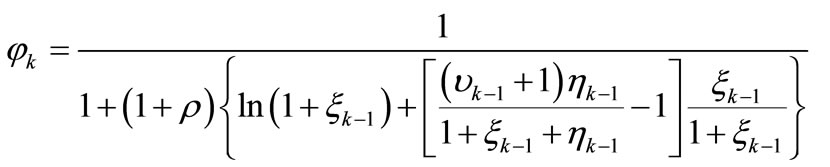 (17)
(17)
with
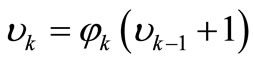 (18)
(18)
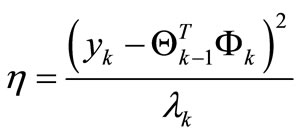 (19)
(19)
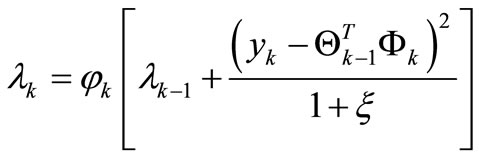 (20)
(20)
5. Minimum Variance Controller (MVC) for 2-Axes PAM Manipulator
Consider the plant described by:
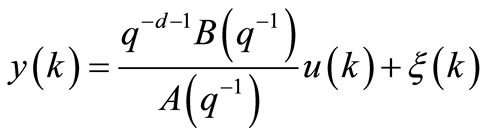 (21)
(21)
where y(k) is the output of the plant, u(k) represents the input of the process, ξ(k) is the disturbance acting on the plant output, d is the time delay of the plant in samples (d 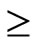 0) and the polynomials A & B are given by:
0) and the polynomials A & B are given by:
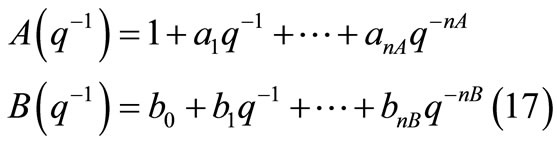
where nA and nB are the degrees of the polynomials A and B.
The controller output is assumed to be calculated using the following equation:
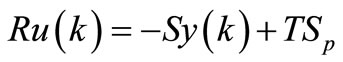 (22)
(22)
with R, S and T are polynomials in q-1, R is monotonic and Sp is the set-point. The closed-loop system presents (21) and (22) results as depicted in Figure 7.
From this diagram follows that:
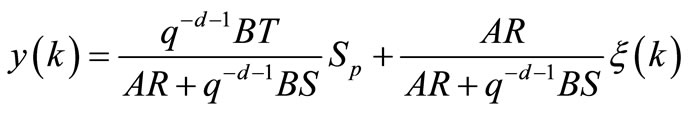 (23)
(23)
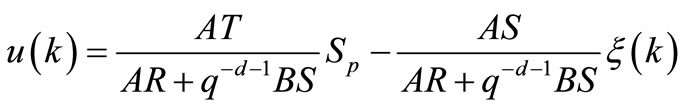 (24)
(24)
In pole-placement design the controller polynomials R and S are calculated such that the closed-loop poles appear at the desired locations. These locations are often specified by the polynomials Pd and C; R and S are then solved from:
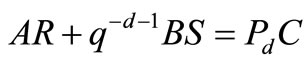 (25)
(25)
The polynomial C is called the observer polynomial (whose roots must be inside the unit circle) and (25) is called the Diophantine equation. In order to solve R and S from (25), it can often use the Euclid’s algorithm. Fur
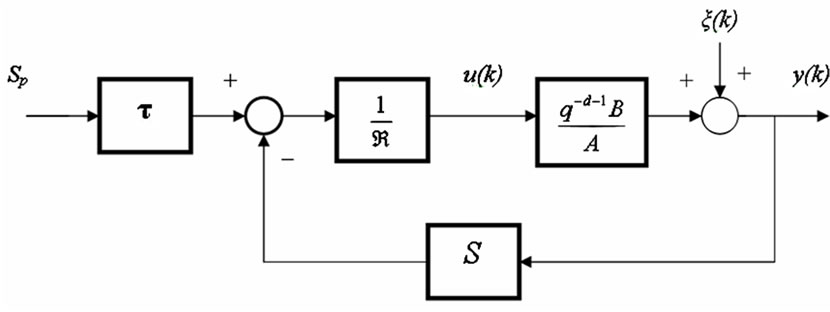
Figure 7. The discrete closed-loop system of PAM manipulator applied MVC.
thermore, T is selected such that the system behavior is as desired. Generally, T is selected as:
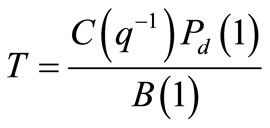 (26)
(26)
When using MVC, Pd = B/b0 and T = C/b0. From (25) it follows, using the assumption d = 0, that R and S must satisfy the following equation:
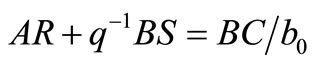 (27)
(27)
It can be verified that the minimum-degree solution of (27) will be given by:
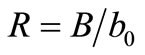 (28)
(28)
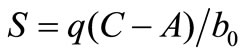 (29)
(29)
The closed-loop transfer functions (23) and (24) then become:
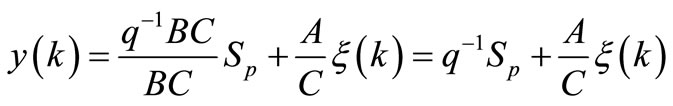 (30)
(30)
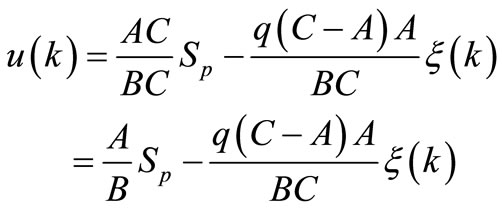 (31)
(31)
and if the process is an ARX process, i.e.
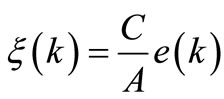 , then (23) and (24) become:
, then (23) and (24) become:
 (32)
(32)
6. Configuration of the PAM Manipulator
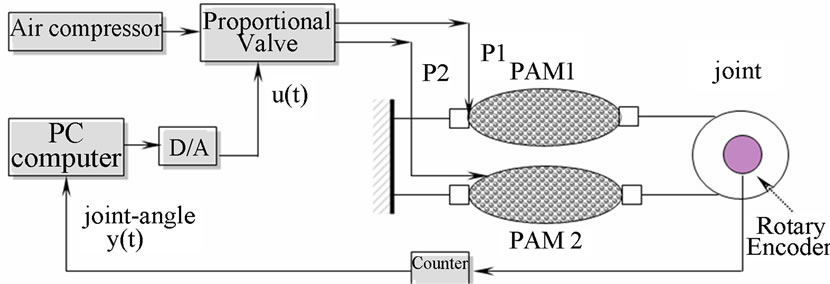
A general configuration of PAM manipulator, the schematic diagram of the PAM manipulator and the photograph of the experimental apparatus are shown in Figure 8(a), Figure 8(b) and Figure 9(a), respectively.
The aim of this paper is multi-purposed. Firstly, the proposed MGA algorithm will be applied for identify the 2nd order ARX model of the PAM manipulator. The se-cond purpose from this resulting ARX model is to compare the performance between MGA with the simple GA algorithm and the conventional LMS method for identifying a1, a2, b1 and b2 parameters of the 2nd order ARX model. The excitation input u(t) to be used is chosen as pseudo random binary sequence (PRBS). The PRBS signal proves the best efficiency signal for identifying a highly nonlinear system. Finally applying MVC controller based on MRLS observer for position control the highly nonlinear PAM manipulator and obtaining
 (a)
(a)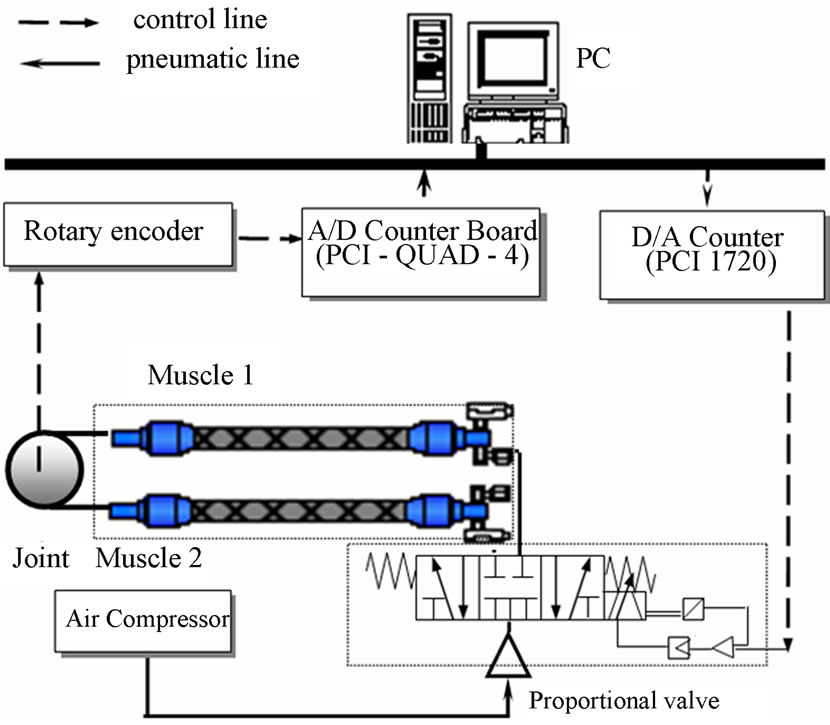 (b)
(b)
Figure 8. (a) Block diagram for obtaining PRBS input-output data of the PAM manipulator; (b) Experimental system of the prototype PAM ma-nipulator.
from simulation and experiment outperforming results in comparison with other control algorithms.
The prototype PAM manipulator is chosen for modeling and identification. Figure 5 presents the block diag-ram for obtaining PRBS training and validating data from the joint of the PAM manipulator. Table 2 presents the configuration of the hardware set-up installed from Figure 5 as to model, identify the 2nd order ARX model of the PAM manipulator and control the PAM manipulator based on adaptive MVC controller. The hardware includes an IBM compatible PC (Pentium 1.7 GHz) which sends the voltage signal to control the proportional valves (FESTO, MPYE-5-1/8HF-710B), through a D/A board (ADVANTECH, PCI 1720 card) which changes digital signals from PC to analog voltage. The rotating torque is generated by the pneumatic pressure difference supplied from air-compressor between the antagonistic artificial muscles. Consequently, the joint of PAM manipulator will be rotated to follow the desired joint angle reference r(t). The joint angle q [deg] is detected by ro-tary encoders (METRONIX, H40-8-3600ZO) and fed back to the computer through a 32-bit counter board
 (a)
(a)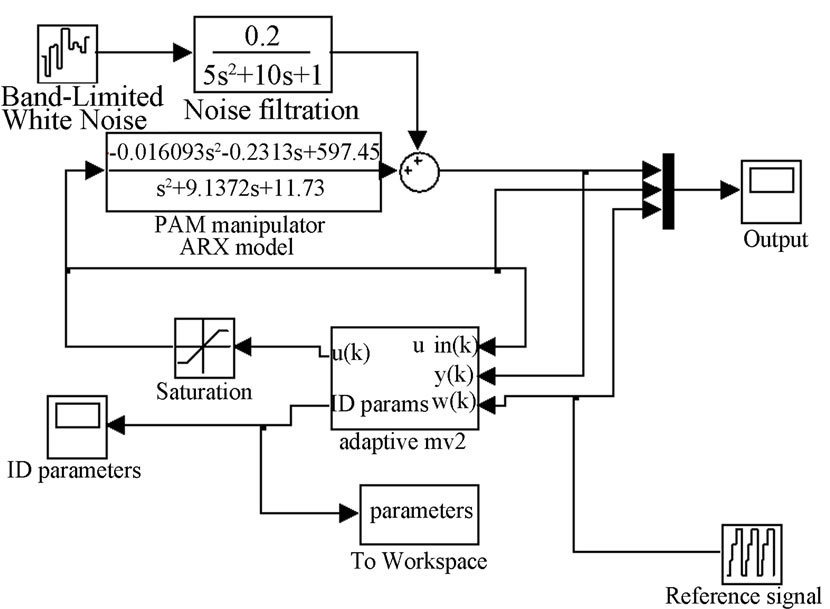 (b)
(b)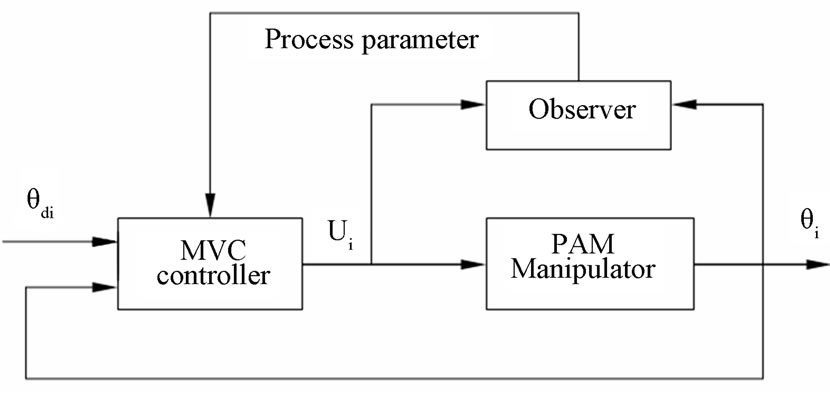 (c)
(c)
Figure 9. (a) Photograph of the experimental 2-Axes PAM manipulator; (b) SIMULINK diagram of the PAM manipulator trajectory tracking using MVC controller; (c) PAM manipulator MVC position control.
(COMPUTING MEASUREMENT, PCI QUAD-4 card) which changes digital pulse signals to joint angle values. The pneumatic line is conducted under the pressure of 5 [bar] and the software control algorithm of the closed-loop system is coded in C-mex program language run in Real-Time Windows Target of MATLAB-SIMULINK
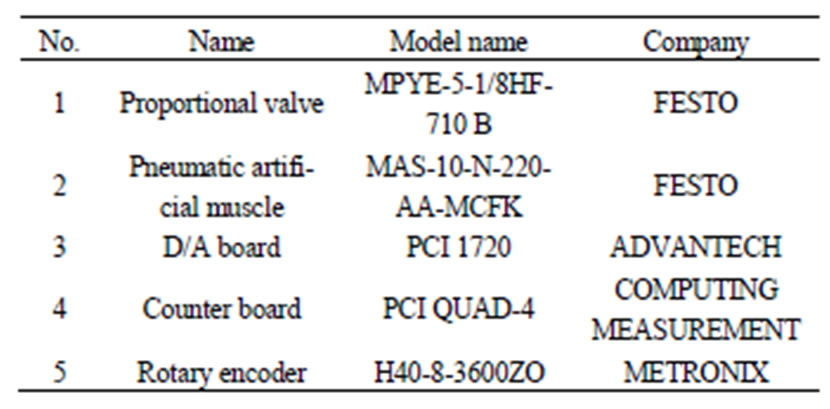
Table 2. The lists of experimental hardware
environment. A schematic diagram of the experimental apparatus is shown in Figure 9(b). Table 2 presents the configuration of the hardware set-up installed from Figure 8 and Figure 9 as to control of the 2nd Joint of the PAM system using the proposed MVC control algorithm.
7. Experiment Results Using MVC Control
In this section, a MVC controller (Minimum Variance Controller) [26] based on the MRLS observer is taken in order to verify the accuracy of the PAM manipulate or model using MGA-based identification method. The performance of MVC controller bases on the model of the process. ARX model’s parameters are explicitly used to design the controller. The outperforming performance of MVC control on the PAM manipulator will be proved in the position tracking the PAM manipulator. Figure 8 and Figure 9 show the investigated PAM manipulator system.
The conception of the MVC control is very subtle and efficient. The control input value is decided from the current joint angle value and the desired joint angle value in the next sampling interval. The SIMULINK block diagram of the MVC controller is shown in Fig.9b and Figure 9(c).
The experimental results will be carried out as follows. A variety of reference joint angle trajectory is added to the joint of the PAM manipulator. In this paper, the joint angle values for position tracking of the joint of the PAM manipulator compose both of ladder trajectory as shown in Figure 10 and sinusoidal trajectory as shown in Figure 11. Each experiment is executed for 20 seconds.
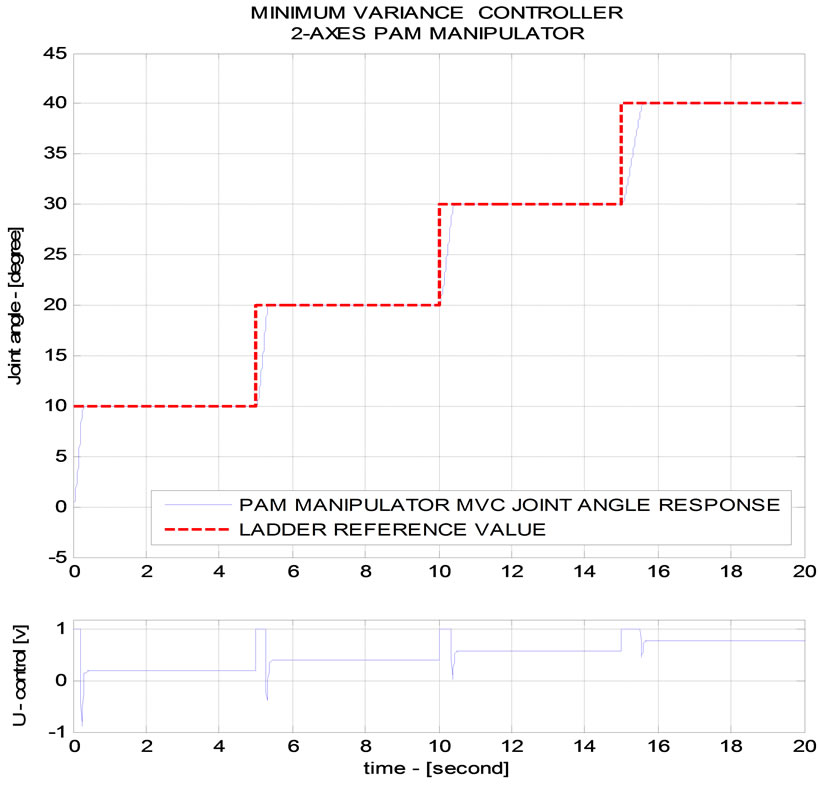
Figures 10 (a) and 10(b) show that a1, a2, b1 and b2 parameters of PAM manipulator ARX model adapt online self-tuning very well at every time appears rising step re-ference (at t = 5 s, 10 s, 15 s respectively). Consequently, MVC in modifying U control flexibly tracks well joint angle ladder trajectory response.
Figure 11(a) and 11(b) prove that MVC controller obtains superb performance. With external disturbance is injected at time t = 11[s], a1, a2, b1 and b2 parameters of ARX model perform online self-tuning well. Conse-
 (a)
(a)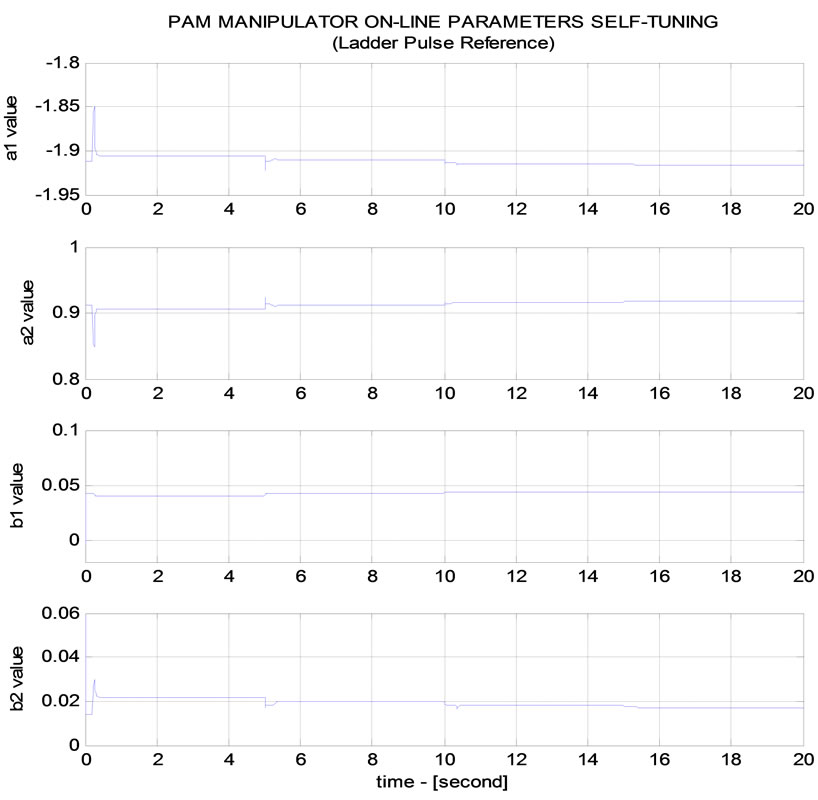 (b)
(b)
Figure 10 (a) PAM manipulator MVC CONTROLLER (Online parameter self-tuning-ladder step trajectory); (b) PAM manipulator MVC CONTROLLER (Online parameter self-tuning-ladder step trajectory tracking).
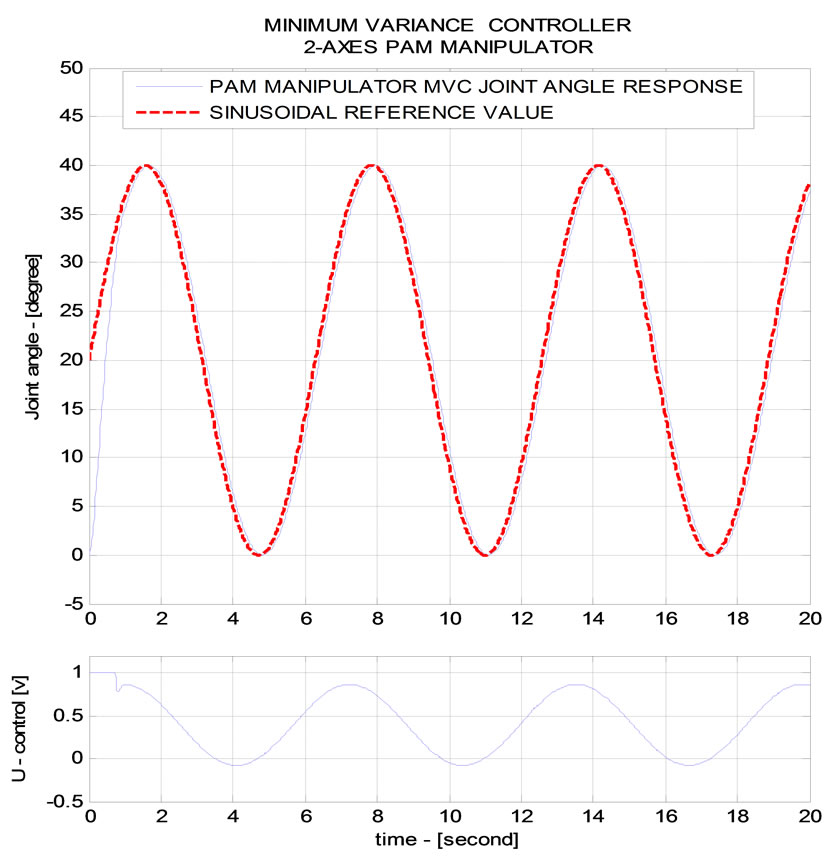
quently, sinusoidal trajectory tracking result is still gua-ranteed excellently.
Forwardly, Figure 12 proves that MVC controller well performs in case of ladder trajectory tracking. With external disturbance is injected at time t = 15 [s], a1, a2, b1 and b2 parameters of ARX model well perform online self-tuning. Consequently, ladder trajectory tracking re-sult is still guaranteed excellently.
Continually, Figure 13(a) and 13(b) prove that MVC
 (a)
(a)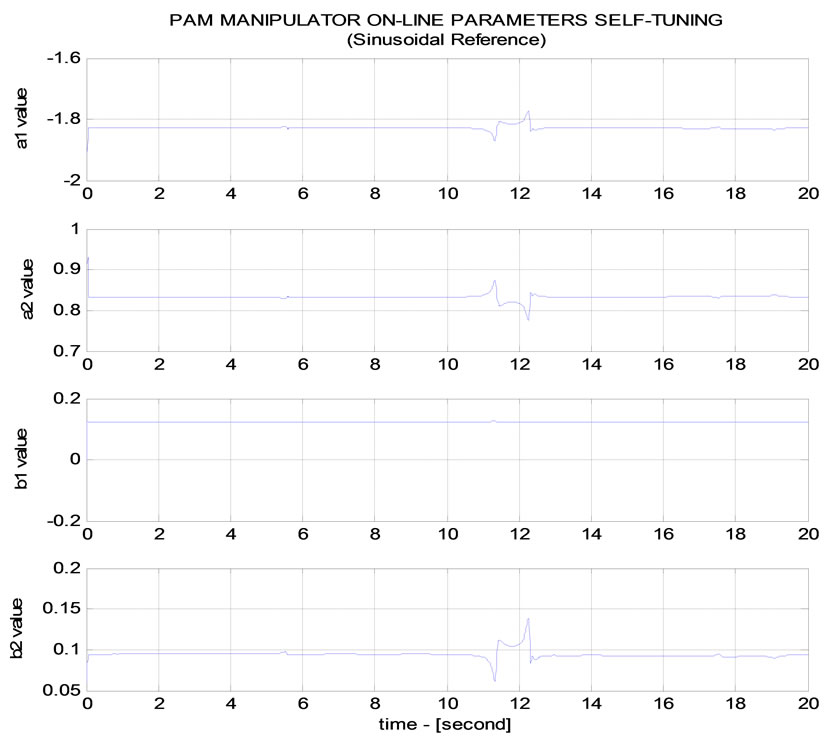 (b)
(b)
Figure 11. (a) PAM manipulator MVC CONTROLLER (Online parameter self-tuning-sinusoidal trajectory); (b) PAM Manipulator MVC CONTROLLER (Online parameter self-tuning-sinusoidal trajectory).
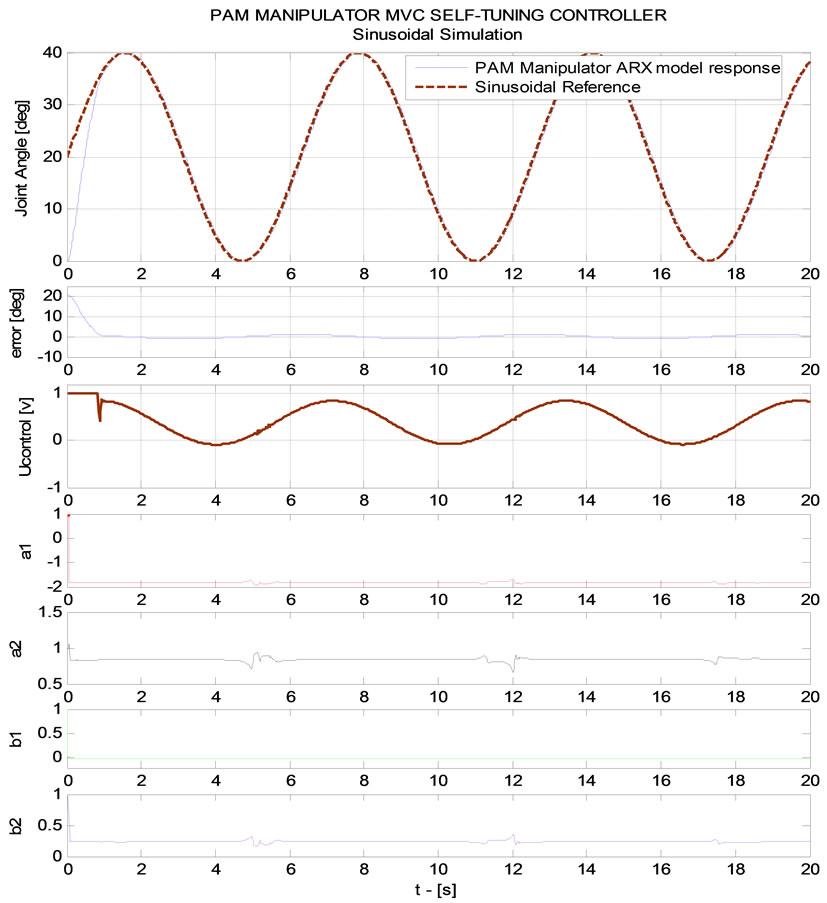
controller obtains outstanding performance in case of si-nusoidal trajectory tracking. With external disturbance is injected at time t = 5 [s] and t = 11 [s], a1, a2, b1 and b2 parameters of ARX model perform good online self-tuning capacity. Consequently, sinusoidal trajectory tra-cking result is still excellently ensured.
Forwardly, Figure 14 continues to prove that MVC controller obtains perfect performance in case of sinusoidal trajectory tracking. With permanent high load and
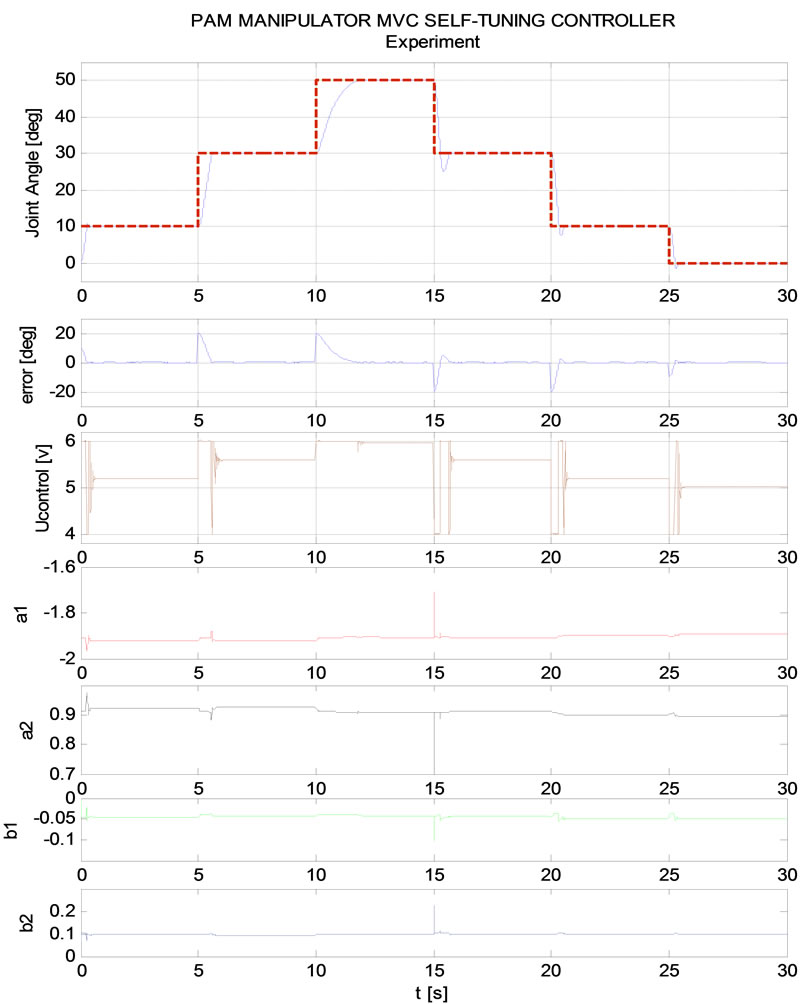
Figure 12. PAM manipulator MVC control –λ = 0.97 (Online parameter self-tuning-ladder trajectory).
external disturbance injected at time t = 11 [s], a1, a2, b1 and b2 parameters of ARX model perform perfectly online self-tuning. Consequently, sinusoidal trajectory tra-cking result is still well guaran-teed.
Finally, Figure 15 assures that MVC controller obtains good performance in case of ladder trajectory during time t = 25 [s] to t = 30 [s], a1, a2, b1 and b2 parameters of ARX model realize their perfect online self-tu-ning capacity. Consequently, ladder trajectory tracking result is always well guaranteed.
Most important remarks are derived from the experiment results. Firstly, the adaptive MVC controller pro-ves superb performance on joint angle position tracking a highly nonlinear PAM manipulator due to perfect online self-tuning capacity of ARX model a1, a2, b1 and b2 b2 parameters. Secondly, the joint angle response with the MVC controller obtains really satisfied settling time and rise time as well. Thirdly, joint angle tracking error of the MVC controller shows an outperforming way with zero steady state error. Finally, the proposed MGA-based identified model as well as MVC controller derived from resulting proposed model has been applied successfully to the joint angle position control over a highly nonlinear system like the PAM manipulator in this study.
8. Conclusions
This paper provides a simple and effective method,
 (a)
(a)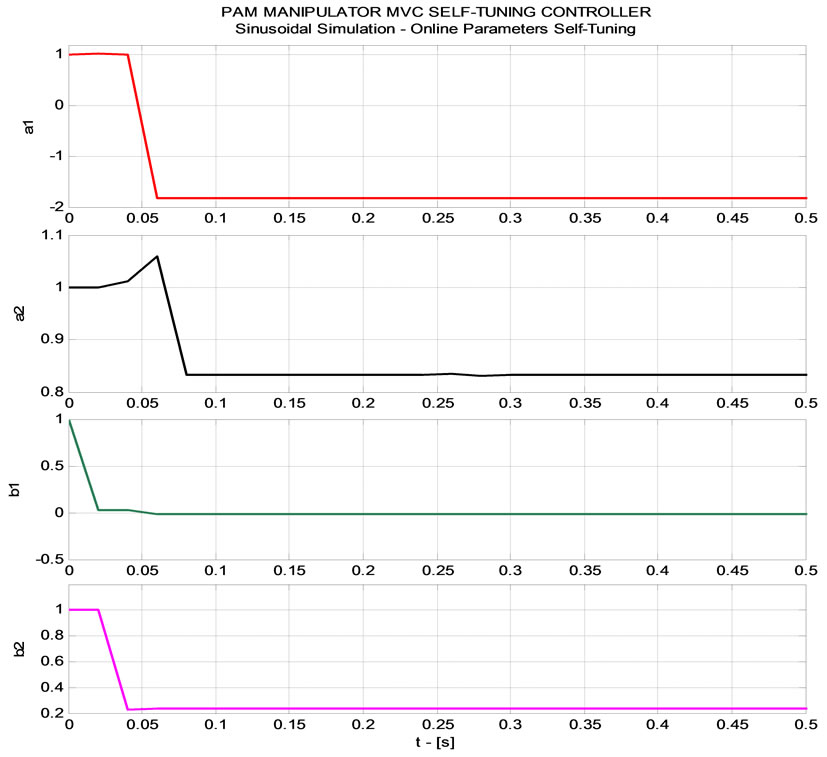 (b)
(b)
Figure 13. (a) PAM manipulator MVC control –λ = 0.99 (Online parameter self-tuning-ladder trajectory); (b) PAM manipulator MVC control –λ = 0.99 (Online parameter self-tuning-sinusoidal trajectory tracking-zooming [0-0.5] (s)).
namely MGA-based system identification, for identifying and controlling a highly nonlinear PAM manipulator. Through experimental investigation, the proposed MGAbased identification algorithm achieves excellent perfor-mance. Online tuning ARX model-based observer can be used to describe the dynamics of the system very well. In addition, the proposed MVC controller is applied ba-
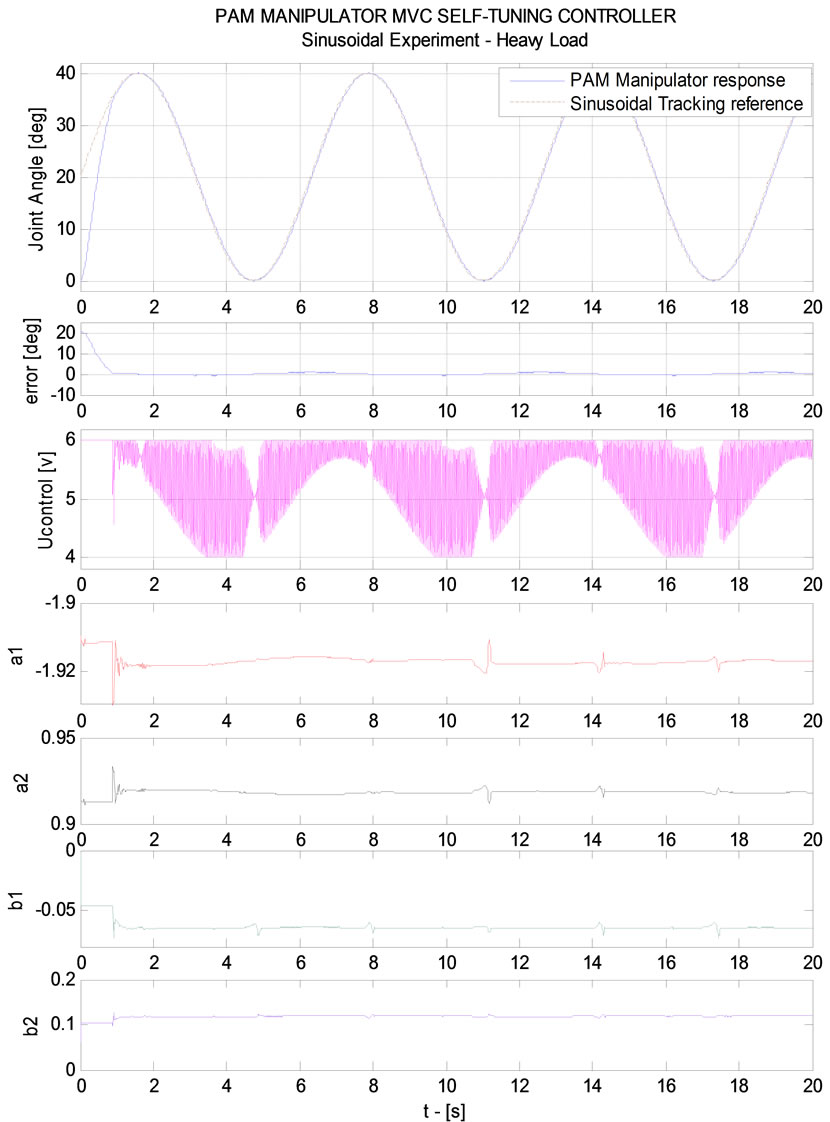
Figure 14. PAM manipulator MVC control –λ = 0.99 (Online parameter self-tuning-sinusoidal trajectory).
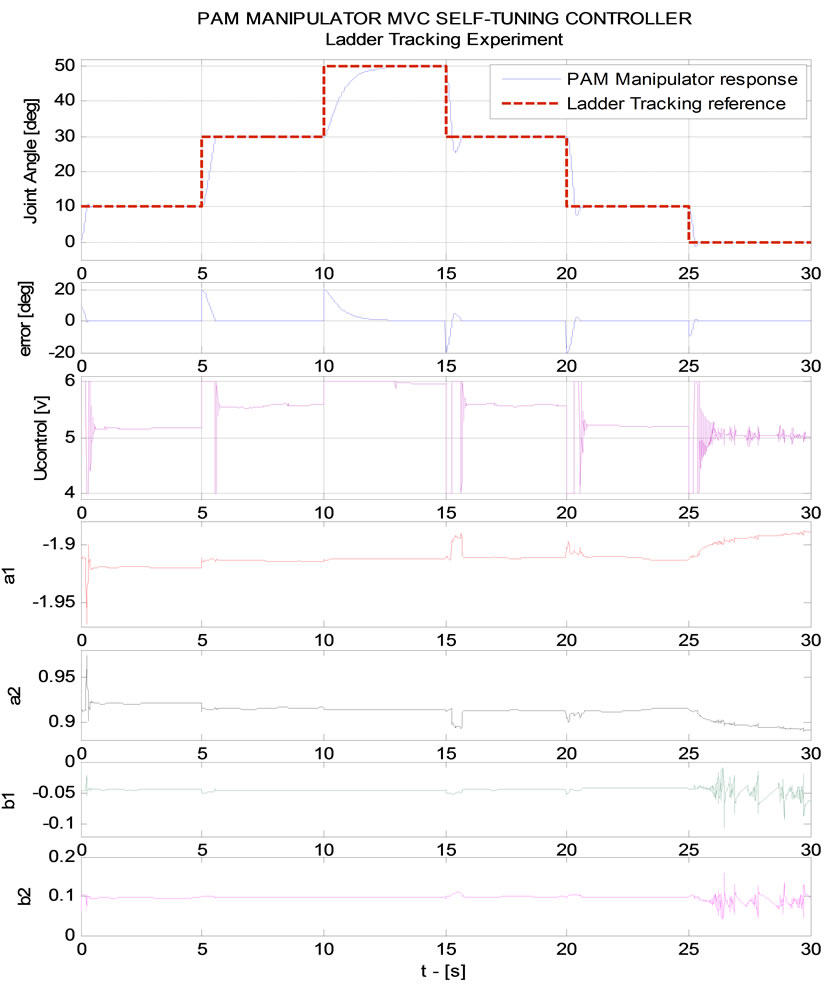
Figure 15. PAM Manipulator MVC Control –λ = 0.99 (Online parameter self-tuning-ladder trajectory).
sed on online tuning ARX model-based observer. Experiment results prove that MVC controller possesses less settling time, zero overshoot, small rise time as well as quite accurate joint angle trajectory tracking. Consequen-tly, novel proposed identification and control method has overcome successfully such intrinsic nonlinear features (like hysteresis, friction,…) of PAM system and thus has excellently improved the performance of the PAM manipulator. These results can be applied to model, identify and control not only the PAM manipulator but also other nonlinear and time-varying industrial systems.
9. Acknowledgements
This paper was supported by DCSELAB, HCM City University of Technology, Ho Chi Minh City, Viet Nam.
10. REFERENCES
- D. G. Caldwell, G. A. Medrano-Cerda and M. Goodwin, “Control of Pneumatic Muscle Actuators,” IEEE Control Systems Magazine, Vol. 1, No. 1, 1995, pp. 40-48. doi:10. 1109/37.341863
- D. W. Repperger, C. A. Phillips, et al., “Power/Energy Metrics for Controller Evaluation of Actuators Similar to Biological Systems,” Mechatronics, Vol. 15, No. 4, May 2005, pp. 459-469. doi:10.1016/j.mechatronics.2004.10. 002
- D. W. Repperger, C. A. Phillips, D. C. Johnson, R. D. Harmon and K. Johnson, “A Study of Pneumatic Muscle Technology for Possible Assistance in Mobility,” Proceedings of 19th Annual International Conference IEEE Engineering in Medicine and Biology Society, Chicago, 1997, pp. 1884-1887.
- B. J. Ruthenberg, N. A. Wasylewski and J. E. Beard, “An Experimental Device for Investigating the Force and Power Requirements of a Powered Gait Orthosis,” Journal of Rehabilitation Research & Development, Vol. 34, No. 2, 1997, pp. 203-213.
- G. R. Johnson and M. A. Buckley, “Development of a New Motorized Upper Limb Orthotic System (MULOS),” Proceedings of Rehabilitation Engineering Society North America, Pittsburgh, 1997, pp. 399-401.
- G. Colombo, M. Joerg, R. Schreier and V. Dietz, “Treadmill Training of Paraplegic Patients Using a Robotic Orthosis,” Journal of Rehabilitation Research & Development, Vol. 37, No. 6, 2000, pp. 693-700.
- B. Tondu and P. Lopez, “Modeling and Control of McKibben Pneumatic Artificial Muscle Robot Actuators,” IEEE Control Systems Magazine, Vol. 20, No. 2, 2000, pp. 15-38. doi:10.1109/37.833638
- C. P. Chou and B. Hannaford, “Measurement and Modeling of McKibben Pneumatic Artificial Muscles,” IEEE Transaction on Robotics and Automation, Vol. 12, No. 1, 1996, pp. 90-102. doi:10.1109/70.481753
- D. B. Reynolds, D. W. Repperger, C. A. Phillips and G. Bandry, “Modeling the Dynamic Characteristics of Pneumatic Muscle,” Annals of Biomedical Engineering, Vol. 31, 2003, pp. 310-317. doi:10.1114/1.1554921
- K. K. Ahn and T. D. C. Thanh, “Intelligent Phase Plane Switching Control of Pneumatic Artificial Muscle (PAM) Manipulators with Magneto-Rheological Brake,” Mechatronics, Vol. 16, No. 2, March 2006, pp. 85-95. doi: 10.1016/j.mechatronics.2005.10.001
- K. K. Ahn and H. P. H. Anh, “System Modeling and Identification of the Two-Link Pneumatic Artificial Muscle (PAM) Manipulator Optimized with Genetic Algorithm,” Proceedings 2006 of IEEE-ICASE International Conference, Busan, 2006, pp. 4744-4749.
- K. K. Ahn and H. P. H. Anh, “Identification of the Pneumatic Artificial Muscle Manipulators by MGA-Based Nonlinear NARX Fuzzy Model,” International Journal of Mechatronics, Vol. 19, No. 1, February 2009, pp. 106-133. doi:10.1016/j.mechatronics.2008.06. 004
- J. Lilly, “Adaptive Tracking for Pneumatic Muscle Actuators in Bicep and Tricep Configurations,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, Vol. 11, No. 3, 2003, pp. 56-63. doi:10.1109/ TNSRE.2003.816870
- G. A. Cerda, C. J. Bowler and D. G. Caldwell, “Adaptive Position Control of Antagonistic Pneumatic Muscle Actuators,” Proceedings of IEEE International Conference on Intelligent Robots and Systems, Pittsburgh, Vol. 1, 5-9 August 1995, pp. 378-383.
- R. Q. van der Linde, “Design, Analysis, and Control of a Low Power Joint for Walking Robot by Phasic Activation of McKibben Muscle,” IEEE Transactions on Robotics and Automation, Vol. 15, No. 4, 1999, pp. 599-604. doi:10.1109/70.781963
- D. G. Caldwell, G. A. Medrano-Cerda and M. Goodwin, “Braided Pneumatic Muscle Actuator Control of a Multi-Jointed Manipulator,” Proceedings of IEEE Systems, Man, and Cybernetics Conference, Le Touquet, Vol. 1, 17-20 October 1993.
- T. Hesselroth, K. Sarkar, P. Van der Smagt and K. Schulten, “Neural Network Control of a Pneumatic Robot Arm,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 24, No. 1, 1994, pp. 28-38. doi:10.1109/21. 259683
- D. W. Repperger, C. A. Phillips and M. Krier, “Controller Design Involving Gain Scheduling for a Large Scale Pneumatic Muscle Actuator,” Proceedings of IEEE Conference on Control Applications, Kohala Coast, 22-27 August 1999, pp. 234-241.
- S. W. Chan, J. Lilly, D. W. Repperger and J. E. Berlin, “Fuzzy PD+I Learning Control for a Pneumatic Muscle,” Proceedings of 2003 IEEE International Conference on Fuzzy Systems, St. Louis, 9 July 2003, pp. 278-283.
- X. Chang and J. H. Lilly, “Tracking Control of a Pneumatic Muscle by an Evolutionary Fuzzy Controller,” Intelligent Automation and Soft Computing, Vol. 9, No. 3, 2003, pp. 227-244.
- P. Carbonell, Z. P. Jiang and D. W. Repperger, “A Fuzzy Back-Stepping Controller for a Pneumatic Muscle Actuator System,” Proceedings of IEEE International Symposium on Intelligent Control, Mexico City, 5-7 September 2001, pp. 353-358.
- M. Hamerlain, “An Anthropomorphic Robot Arm Driven by Artificial Muscles Using a Variable Structure Control,” Proceedings of IEEE International Conference Intelligent Robots Systems, Pittsburgh, Vol. 1, 5-9 August 1995, pp. 550-555.
- D. W. Repperger, K. R. Johnson and C. A. Phillips, “A VSC Position Tracking System Involving a Large Scale Pneumatic Muscle Actuator,” Proceedings of IEEE 37th Conference Decision Control, Tampa, Vol. 4, 16-18 December 1998, pp. 4302-4307.
- J. J. Slotine and S. Sastry, “Tracking Control of Nonlinear System Using Sliding Surface with Application to Robot Manipulators,” International Journal of Control, Vol. 38, No. 2, 1993, pp. 465-492. doi:10.1080/0020717 8308933088
- K. Osuka, T. Kimura and T. Ono, “Ha Control of a Certain Nonlinear Actuator,” Proceedings of IEEE Conference on Decision Control, Honolulu, 5-7 December 1990, pp. 370-371.
- Z. Li, B. Wittenmark and R. J. Evans, “Minimum Variance Prediction for Linear Time-Varying Systems,” Automatica, Vol. 33, No. 4, 1998, pp. 607-618. doi:10. 1016/S0005-1098(96)00210-5

