Intelligent Control and Automation
Vol.06 No.01(2015), Article ID:53285,6 pages
10.4236/ica.2015.61005
No-Wait Flowshops to Minimize Total Tardiness with Setup Times
Tariq Aldowaisan, Ali Allahverdi
Department of Industrial and Management Systems Engineering, Kuwait University, Kuwait City, Kuwait
Email: tariq.aldowaisan@ku.edu.kw, ali.allahverdi@ku.edu.kw
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 December 2014; accepted 5 January 2015; published 15 January 2015
ABSTRACT
The m-machine no-wait flowshop scheduling problem is addressed where setup times are treated as separate from processing times. The objective is to minimize total tardiness. Different dispatching rules have been investigated and three were found to be superior. Two heuristics, a simulated annealing (SA) and a genetic algorithm (GA), have been proposed by using the best performing dispatching rule as the initial solution for SA, and the three superior dispatching rules as part of the initial population for GA. Moreover, improved versions of SA and GA are proposed using an insertion algorithm. Extensive computational experiments reveal that the improved versions of SA and GA perform about 95% better than SA and GA. The improved version of GA outperforms the improved version of SA by about 3.5%.
Keywords:
No-Wait Flowshop, Scheduling, Setup Times, Total Tardiness, Simulated Annealing, Genetic Algorithm

1. Introduction
In a no-wait flowshop environment, jobs are processed continuously from start to end without interruptions either on or between machines. Therefore, the start of a job on a given machine may be delayed to ensure that its operation completion coincides with the start of its subsequent operation on the next machine. Applications of such an environment are found in several industries; e.g., metal, plastic, chemical, and semiconductor. Ref. [1] surveyed the applications and research on the no-wait flowshop environment.
The m-machine no-wait flowshop problem has been addressed with respect to several performance measures including makespan and total completion time. For the makespan, examples of research are Refs. [2] - [9] . For separate setup times and makespan performance measure, see Ref. [10] . As for the total completion time, some of the works include Refs. [5] [11] - [13] . Ref. [14] proposed a constructive heuristic for minimizing total flowtime where setup times were considered as separate.
While makespan and total completion time are directly related to job completion times, other measures such as number of tardy jobs, maximum tardiness, and total tardiness are more focused on job due dates. Recent research on the latter type of measures includes Refs. [15] - [17] . Ref. [17] proposed six different heuristics for minimizing total tardiness. Ref. [16] considered both makespan and maximum tardiness where the objective is to find approximations of Pareto front by using simulating annealing. Ref. [15] proposed several heuristics for the m-machine no-wait flowshop problem with respect to the number of tardy jobs. It is important to note that the minimization of the number of tardy jobs directly affects costs associated with late delivery as well as the percentage of on-time shipments, which is often used to appraise managers’ performance. Unlike the number of tardy jobs, the total tardiness measure accounts for the duration of delay which has financial as well as reputation and good will impacts. In many practical situations, the cost increases with the delay duration. This increase may take the form of financial penalties corresponding to different time period delays. Therefore, total tardiness is a more appropriate measure for such situations.
Ref. [18] addressed the m-machine no-wait scheduling problem with respect to the total tardiness performance measure, where they proposed several efficient heuristics. However, they did not consider setup time which was relevant in some industries. Ref. [19] pointed out the significance of considering setup times and Refs. [20] and [21] provided a survey of the research on scheduling with setup times.
2. Notation
For the m-machine no-wait flowshop, we assume that the set of n jobs are ready for processing at time zero. Each job 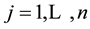 has to be processed continuously in the same order on a set of
has to be processed continuously in the same order on a set of 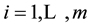 machines without interruptions either on or between machines. The following notation will be used.
machines without interruptions either on or between machines. The following notation will be used.
E: tardiness factor.
R: due date range factor.
dj: due date of job j; which is generated using the E and R factors.
Cj: completion time of job j on the last machine.
Tj: tardiness of job j; where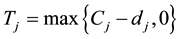 .
.
Pij: processing time of job j on machine i.
Sij: setup time of job j on machine i.
The objective is to sequence all jobs to minimize the total tardiness.
3. Dispatching Rules
Dispatching rules are simple heuristics for building a schedule. Their popularity is due to their ability to rapidly provide good solution in practical production settings. They are also used as initial sequences for the proposed heuristics in the next section. A number of well-known dispatching rules have been initially investigated with regard to the considered criterion. Three of the considered dispatching rules outperformed the others. The following is an explanation of the three.
Let s denote the sequence of jobs which are scheduled so far and t denote the time at which jobs need to be selected. Moreover, let Cj(s) denote the completion time of job j considered for scheduling (not in s yet) if it is scheduled as the last job in the sequence s.
1. Earliest due date with processing and setup times (EDDP); where jobs are sequenced in non-decreasing order of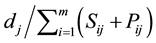 .
.
2. Modified due date (MDD); where jobs are sequenced in non-decreasing order of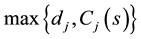 .
.
A third dispatching rule is proposed as follows:
Sequence the jobs with the minimum total tardiness of jobs based on averaging the setup and processing time for each job across all machines (TOTA), reducing it to a single machine problem. The average of the setup and processing time of each job across all machines is first determined, then the sequence is obtained by finding the optimal sequence based on the average setup and processing time for each job. The due date for TOTA is calculated by dividing the due dates associated with the m-machine by the number of machines.
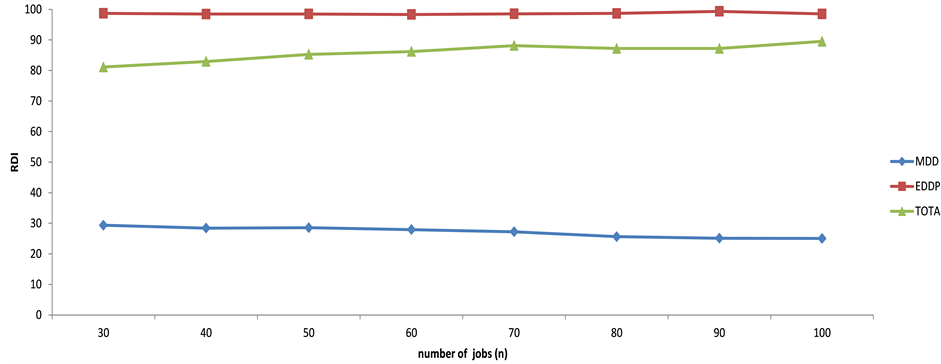
When comparing the three rules of MDD, EDDP, and TOTA, it was found that (see Figure 1) MDD performed best followed by TOTA. For all the considered experimental cases, which will be detailed later, MDD performed about 60% better than TOTA; while TOTA outperformed EDDP by about 15%.
In the next section, we use the MDD as an initial sequence to develop an improved simulated annealing heuristic; and use the three dispatching rules MDD, TOTA, and EDDP as part of the initial generation population to develop an improved genetic algorithm heuristic.
4. Proposed Heuristics FISA2 and FIGA2
[18] proposed a simulated annealing algorithm, called ISA, and a genetic algorithm, called IGA. The same algorithms ISA and IGA of [18] are used here after modifying the various input parameters, including initial sequences, to account for the setup time.
The parameters of ISA and IGA have also been investigated for the separate setup time environment. Experimentations revealed that the parameter values of ISA and IGA which were found to do well in Ref. [18] were also found to perform well in the separate setup environment. Table 1 and Table 2 summarize the tested and selected parameters’ values for the two heuristics.
Figure 1. Comparison of dispatching rules.
Table 1. Selected parameters’ values for ISA.
Table 2. Selected parameters’ values for IGA.
Ref. [18] applied an insertion and exchange procedures to ISA and IGA and obtained better heuristics called FISA and FIGA with about 90% improvement over ISA and IGA.
In this paper, in addition to the one-block procedure used by [18] , we propose a two-block insertion procedure. The following are the steps of the two-block insertion procedure.
Step 1: Use ISA as initial sequence s.
Step 2: Set k = 1.
Step 3: Pick the first two jobs from s and select the better with regard to total tardiness of the two permutations as the current solution.
Step 4: Set k = k + 1.
Step 5: Generate candidate sequences by selecting the next two jobs from s and inserting the two permutations of these two jobs into each position of the current solution. Among the generated candidates, the sequence with the least total tardiness value becomes the current solution.
Step 6: Go to Step 4 until all jobs in s have been considered.
For a problem with odd number of jobs, the last job to be selected will be inserted as a single job in all possible positions in the current solution.
We have investigated the one-block and two-block insertion procedures for the considered problem, the results indicated that the one-block outperforms the two-block one. The resulting two heuristics of applying the one-block insertion and exchange procedures are denoted as FISA2 and FIGA2. The same insertion is used for the FIGA2 by replacing ISA with IGA in Step 1.
5. Computational Analysis
In this section we conduct experiments to first study the effect of the various parameters such as E and R, and evaluate the performances of the proposed heuristics against each other. The experiments were performed on a PC running Windows 7 32-bits, with an Intel Dual Core CPU 2.26 GHz and 3 GB RAM. The data generation and testing application were developed using the C# programming language which runs on the top of Microsoft’s NET Framework 3.5. Table 3 describes the experiment parameters and their values.
The considered values E, R, pij, and sij are commonly used in the scheduling literature; e.g. [22] . The due dates
of jobs are generated using the parameters E and R with a uniform distribution between 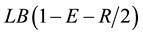 and
and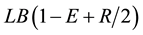 , where LB is a tight lower bound on the makespan.
, where LB is a tight lower bound on the makespan.
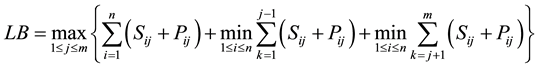
where, 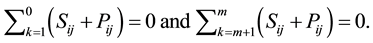
The total number of all possible combinations is 1296 based on the considered values of n, m, E, R, and k; where each combination is replicated 30 times.
The performance measure used for evaluating the heuristics is the relative deviation index (RDI); calculated as follows:
Table 3. Experiment parameters.
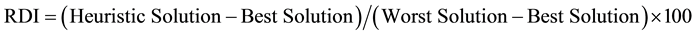
where the Heuristic Solution is the solution obtained by a given heuristic, Best Solution and Worst Solution are the best and worst solutions obtained from among the compared heuristics. The RDI produces a result between 0 and 100; where the best solution will have RDI values closest to 0.
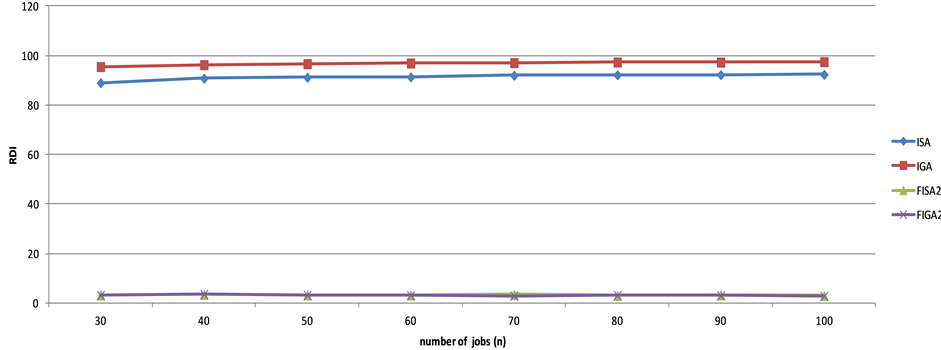
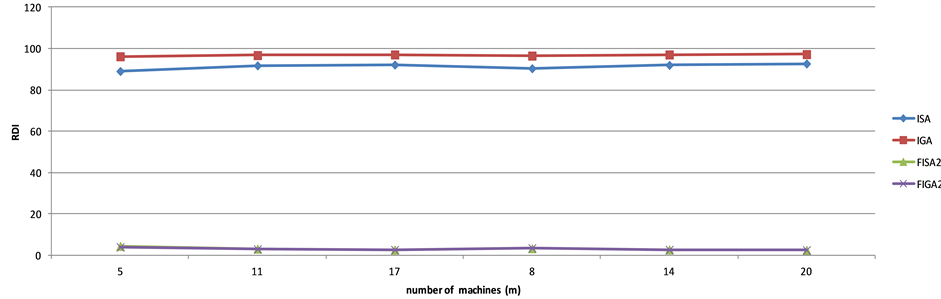
Figure 2 shows the results of the RDI comparison for different number of jobs. The ISA heuristic performed better than IGA by about 6%; however both of them are significantly outperformed by FIGA2 and FISA2 by over 95%. The difference between FIGA2 and FISA2 is not significant; though FIGA2 slightly outperforms FISA2 by less than 3.5%. Figure 3, which shows the performance for different number of machines, yielded similar results. In both Figure 3 and Figure 4, the increase in number of jobs and machines did not show any significant impact on the RDI performance.
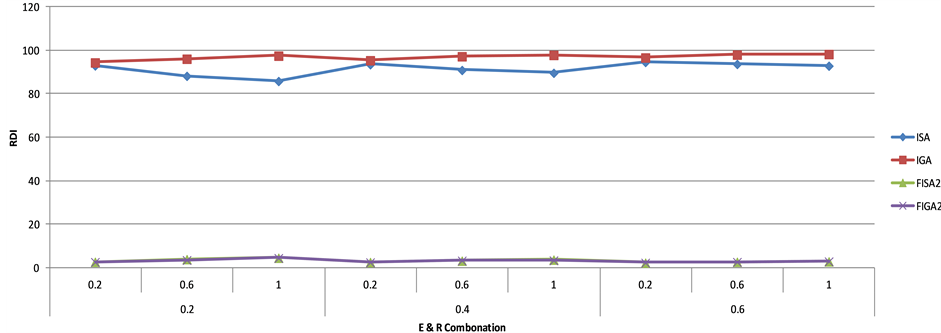
Figure 4 shows that using various E/R combinations has generally low impact on RDI; except for a slight improvement in ISA performance for high E values. With respect to varying the k value to control the setup time duration, it didn’t generally have a significant impact.
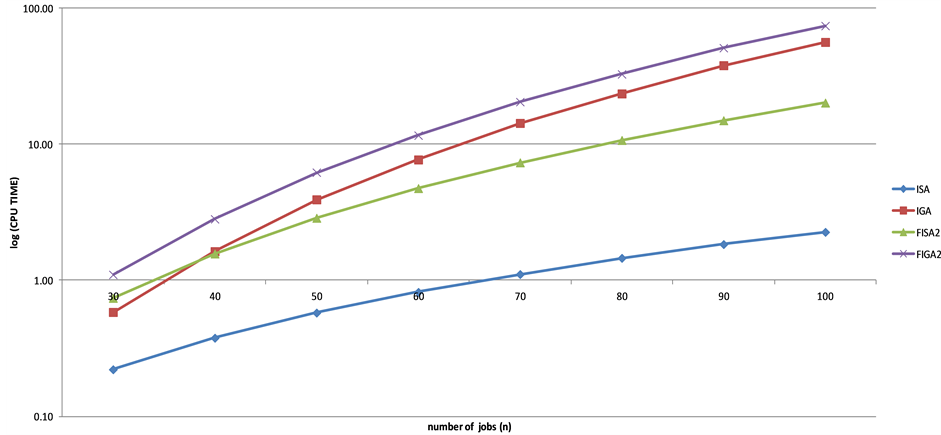
As shown from Figure 5, the computational time for IGA and FIGA2 are higher than the ISA and FISA2 with FIGA2 being the highest and ISA the lowest. For the largest number of jobs n = 100, the computational time for all heuristics is less than 2 seconds. Therefore, computational time is considered negligible.
6. Conclusion
The m-machine no-wait flowshop scheduling problem, where setup times are considered as separate from pro- cessing times, with the objective of minimizing total tardiness has been considered. Different dispatching rules
Figure 2. Comparison of heuristics for RDI criterion vs. n; for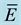 ,
, 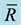
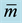
Figure 3. Comparison of heuristics for RDI criterion vs. m; for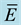
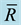
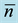
Figure 4. Comparison of heuristics for RDI criterion for different E/R combinations.
Figure 5. The computational time of heuristics for different number of jobs.
have been proposed and three of which, MDD, EDDP, TOTA, have been found performing well. The dispatching rule MDD outperforms TOTA about 60%, which outperforms EDDP about 15%. Furthermore, a simulated annealing algorithm (ISA) and a genetic algorithm (IGA) have been proposed. It has been found that IGA outperforms ISA about 6%. Moreover, improved versions of ISA and IGA have been proposed and it has been found that improved versions outperform ISA and IGA about 95%. Of the improved versions, FIGA2 outperforms FISA2 about 3.5%.
Acknowledgements
This research was supported by Kuwait University Research Administration project number Grant No. EI01/12.
References
- Hall, N.G. and Sriskandarajah, C. (1996) A Survey of Machine Scheduling Problems with Blocking and No-Wait in Process. Operations Research, 44, 510-525. http://dx.doi.org/10.1287/opre.44.3.510
- Aldowaisan, T. and Allahverdi, A. (2003) New Heuristics for No-Wait Flowshops to Minimize Makespan. Computers & Operations Research, 30, 1219-1231. http://dx.doi.org/10.1016/S0305-0548(02)00068-0
- Allahverdi, A. and Aldowaisan, T. (2004) No-Wait Flowshops with Bicriteria of Makespan and Maximum Lateness. European Journal of Operational Research, 152, 132-147. http://dx.doi.org/10.1016/S0377-2217(02)00646-X
- Framinan, J.M. and Nagano, M.S. (2008) Evaluating the Performance for Makespan Minimisation in No-Wait Flowshop Sequencing. Journal of Materials Processing Technology, 197, 1-9. http://dx.doi.org/10.1016/j.jmatprotec.2007.07.039
- Pan, Q.K., Fatih Tasgetiren, M. and Liang, Y.C. (2008) A Discrete Particle Swarm Optimization Algorithm for the No-Wait Flowshop Scheduling Problem. Computers & Operations Research, 35, 2807-2839. http://dx.doi.org/10.1016/j.cor.2006.12.030
- Kalczynski, P.J. and Kamburowski, J. (2007) On No-Wait and No-Idle Flow Shops with Makespan Criterion. European Journal of Operational Research, 178, 677-685. http://dx.doi.org/10.1016/j.ejor.2006.01.036
- Davendra, D., Zelinka, I., Bialic-Davendra, M., Senkerik, R. and Jasek, R. (2013) Discrete Self-Organising Migrating Algorithm for Flow-Shop Scheduling with No-Wait Makespan. Mathematical and Computer Modelling, 57, 100-110. http://dx.doi.org/10.1016/j.mcm.2011.05.029
- Zhu, J., Li, X. and Wang, Q. (2009) Complete Local Search with Limited Memory Algorithm for No-Wait Job Shops to Minimize Makespan. European Journal of Operational Research, 198, 378-386. http://dx.doi.org/10.1016/j.ejor.2008.09.015
- Tseng, L.Y. and Lin, Y.T. (2010) A Hybrid Genetic Algorithm for No-Wait Flowshop Scheduling Problem. International Journal of Production Economics, 128, 144-152. http://dx.doi.org/10.1016/j.ijpe.2010.06.006
- Nagano, M.S., Da Silva, A.A. and Nogueira Lorena, L.A. (2014) An Evolutionary Clustering Search for the No-Wait Flow Shop Problem with Sequence Dependent Setup Times. Expert Systems with Applications, 41, 3628-3633. http://dx.doi.org/10.1016/j.eswa.2013.12.013
- Chen, C.L., Neppalli, R.V. and Aljaber, N. (1996) Genetic Algorithms Applied to the Continuous Flow Shop Problem. Computers & Industrial Engineering, 30, 919-929. http://dx.doi.org/10.1016/0360-8352(96)00042-3
- Aldowaisan, T. and Allahverdi, A. (2004) New Heuristics for m-Machine No-Wait Flowshop to Minimize Total Completion Time. Omega, 32, 345-352. http://dx.doi.org/10.1016/j.omega.2004.01.004
- Chang, J.L., Gong, D.W. and Ma, X.P. (2007) A Heuristic Genetic Algorithm for No-Wait Flowshop Scheduling Problem. Journal of China University of Mining and Technology, 17, 582-586. http://dx.doi.org/10.1016/S1006-1266(07)60150-3
- Nagano, M.S., Miyata, H.H. and Araújo, D.C. (2014) A Constructive Heuristic for Total Flowtime Minimization in a No-Wait Flowshop with Sequence-Dependent Setup Times. Journal of Manufacturing Systems. http://dx.doi.org/10.1016/j.jmsy.2014.06.007
- Aldowaisan, T.A. and Allahverdi, A. (2012) No-Wait Flowshop Scheduling Problem to Minimize the Number of Tardy Jobs. The International Journal of Advanced Manufacturing Technology, 61, 311-323. http://dx.doi.org/10.1007/s00170-011-3659-x
- Jolai, F., Asefi, H., Rabiee, M. and Ramezani, P. (2013) Bi-Objective Simulated Annealing Approaches for No-Wait Two-Stage Flexible Flow Shop Scheduling Problem. Scientia Iranica, 20, 861-872.
- Liu, G., Song, S. and Wu, C. (2013) Some Heuristics for No-Wait Flowshops with Total Tardiness Criterion. Computers & Operations Research, 40, 521-525. http://dx.doi.org/10.1016/j.cor.2012.07.019
- Aldowaisan, T. and Allahverdi, A. (2012) Minimizing Total Tardiness in No-Wait Flowshops. Foundations of Computing and Decision Sciences, 37, 149-162. http://dx.doi.org/10.2478/v10209-011-0009-6
- Allahverdi, A. and Soroush, H.M. (2008) The Significance of Reducing Setup Times/Setup Costs. European Journal of Operational Research, 187, 978-984. http://dx.doi.org/10.1016/j.ejor.2006.09.010
- Allahverdi, A., Gupta, J.N. and Aldowaisan, T. (1999) A Review of Scheduling Research Involving Setup Considerations. Omega, 27, 219-239. http://dx.doi.org/10.1016/S0305-0483(98)00042-5
- Allahverdi, A., Ng, C.T., Cheng, T.E. and Kovalyov, M.Y. (2008) A Survey of Scheduling Problems with Setup Times or Costs. European Journal of Operational Research, 187, 985-1032. http://dx.doi.org/10.1016/j.ejor.2006.06.060
- Vallada, E., Ruiz, R. and Minella, G. (2008) Minimising Total Tardiness in the m-Machine Flowshop Problem: A Review and Evaluation of Heuristics and Metaheuristics. Computers & Operations Research, 35, 1350-1373. http://dx.doi.org/10.1016/j.cor.2006.08.016