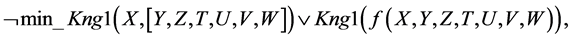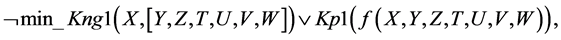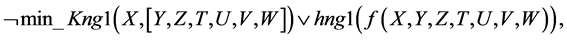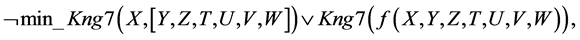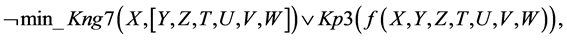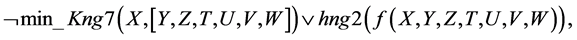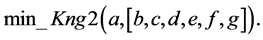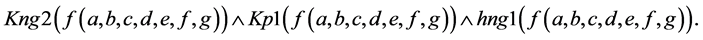Intelligent Control and Automation
Vol.05 No.04(2014), Article ID:51350,8 pages
10.4236/ica.2014.54024
Integrated Expert Analytical System for Assessment of Oil-and-Gas Saturation of Strata
O. G. Nusratov, G. G. Abdullayeva, I. A. Ismayilov
Institute of Cybernetics of the Azerbaijan National Academy of Sciences, Baku, Azerbaijan
Email: ag_gulchin@rambler.ru, r_h_a_i_i@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 September 2014; revised 28 September 2014; accepted 12 October 2014
ABSTRACT
The present research deals with the problem of development of an integrated expert-analytical system for optimum selection of calculated oil-field-geophysical parameters of oil and gas deposits with the purpose of increasing the accuracy of assessment of the reserves of oil and gas deposits. The purpose of the system is to make current adequate decisions on determining of oil-and-gas saturation of strata and future identification of the most significant methods for that, with these methods forming the foundation of knowledge bases for oil-and-gas deposits of the Apsheron pe- ninsula of Azerbaijan. The system architecture allows for expanding the system with its subse- quent transformation into a cluster of expert-analytical systems. A logical model of the proposed system is presented. The paper contains a detailed description of the mechanism of operation of the system as a whole and of its individual blocks. Mathematical and formal-logical bases of the intelligent system are explained. The system is equipped with a tool for dynamic statistical analy- sis of decisions made by it, with representation of the results in real-time mode. The results of the system testing on specific oil-and-gas deposit of the Apsheron peninsula of Azerbaijan in 2013 are given.
Keywords:
Expert System, Knowledge Base, Decision-Making Block, Integrated System, Database, Statistical Analysis Block, Concordance Coefficient, First Order Predicates

1. Introduction
Oil-field-geophysical explorations of wells (GEN) began with the development of resistivity and induced pola- rization methods (developed by C. Schlumberger), which have been in practice since the beginning of the 20th century. Methods and means for determining oil-bearing capacity of strata have been further improved since then, but it was not always possible to get an exact prediction. For instance, 15 commercially sensitive oil- bearing strata were discovered in the South Caspian field at the end of the 20th century. Deep-water drilling op- erations were launched. As a result, rich deposits of gas and condensate were found only in one—Shahdeniz. Other 14 wells and 7 out of 16 wells drilled at the depth between 3840 and 7087 m turned out to be economical- ly ineffective. In 9 wells, no hydrocarbons whatsoever were found [1] . Therefore, development and improvement of methods for determination of oil-and-gas-bearing capacity of strata clearly remain a topical problem.
Expert systems (ES) based on the principles of artificial intelligence (AI) and modern information technolo- gies are among the most developed methods for solving problems of this kind.
Most modern intelligent information and expert systems, e.g. Micromine, Isoline GIS, INGEF, MFS VIKIZ system, EMP Pro, ES “GEOFBI”, GIS-“PRAIM” etc. [2] [3] tend to versatility, which contradicts the basic con- cept of expert system stating the well-known rule: the narrower is the application domain of an expert system, the more precise are its decisions.
In most modern ES, special tools are used, such as expert shells (ES with empty knowledge base), which of- ten causes the opposite effect and only complicates the process of ES development [4] [5] .
2. Problem Statement
This research deals with the problem of development of an integrated expert-analytical system (IEAS) for opti- mum selection of calculated oil-field-geophysical parameters of oil and gas deposits with the purpose of in- creasing the accuracy of assessment of the reserves of oil and gas deposits. In calculating oil and gas reserves, parameters obtained as a result of oil-field-geophysical exploration of wells are used as the principal ones among other initial data.
At gas and oil deposits of Azerbaijan, spontaneous polarization and resistivity logging methods are most often employed at the beginning of the mining. The lithological peculiarities of productive width section (using a par- ticular deposit of the Apsheron peninsula as an example) were taken into consideration in this research when se- lecting the method of determining the effective oil-and-gas saturated thickness of collectors hog. These deposits correspond to the so-called layered model for which hog is determined from the overall thickness of collector 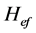 minus the total thickness of argillaceous and non-productive interlayers composing these strata.
minus the total thickness of argillaceous and non-productive interlayers composing these strata.
 (1)
(1)
The total thickness of the argillaceous interlayers 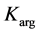 was determined by two methods for the purpose of control:
was determined by two methods for the purpose of control:
by “anisotropy” method
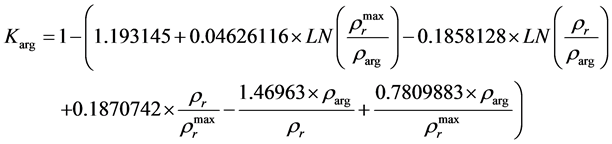 (2)
(2)
where 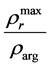 is the ratio of maximum specific electrical resistance of “pure” (clay-free) oil-and-gas bearing
is the ratio of maximum specific electrical resistance of “pure” (clay-free) oil-and-gas bearing
stratum to resistance of clays;
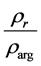 is the ratio of true stratum resistance to resistance of clays;
is the ratio of true stratum resistance to resistance of clays;
by using relative amplitude of natural polarization in a well
 (3)
(3)
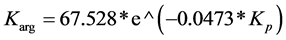 (4)
(4)
where 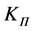 is porosity determined by the following formula:
is porosity determined by the following formula:
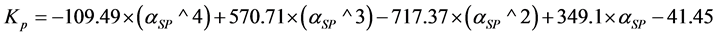 (5)
(5)
The porosity of collectors was determined with consideration for the argillic nature and heterogeneity of silt and sand rocks of productive width of the deposit by two ways:
ü from the curve of porosity-relative amplitude  dependence obtained by means of core data according to Formula (5);
dependence obtained by means of core data according to Formula (5);
ü through computations according to S. G. Komarov’s universal formula. In doing so, it was assumed that po- rosity of a heterogeneous rock is constituted by open porosity and penetrability of silt and sand component of the rock plus porosity of its argillaceous ingredients contained in rocks both in the form of interlayers and in scattered state
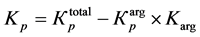 (6)
(6)
where 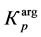 is porosity of clays taken from the cores;
is porosity of clays taken from the cores;
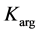 isargillic content determined from
isargillic content determined from 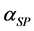 or by “anisotropy” method;
or by “anisotropy” method;
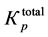 is the total porosity determined from the core data.
is the total porosity determined from the core data.
The oil-and-gas saturation coefficient of rocks was determined by three methods:
1. According to S. G. Komarov’s formula
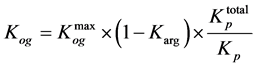
where 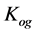
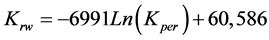
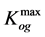
2. By 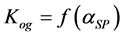
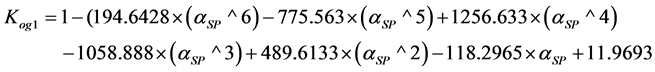
3. Based on Archy’s Formula
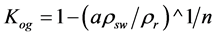
where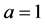
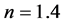
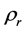
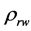
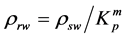
where 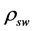
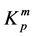
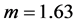
The purpose of the developed IEAS is to make current adequate decisions on determining of oil-and-gas sa- turation of strata and future identification of the most significant methods for that, with these methods forming the foundation of knowledge bases for oil-and-gas deposits. Thus, the system architecture allows for expanding the system through its integration with additional expert systems with subsequent transformation into a cluster of integrated expert-analytical systems (BIEAS) for the most extensive coverage of oil-and-gas deposits of the Ap- sheron peninsula of Azerbaijan.
3. Problem Solving
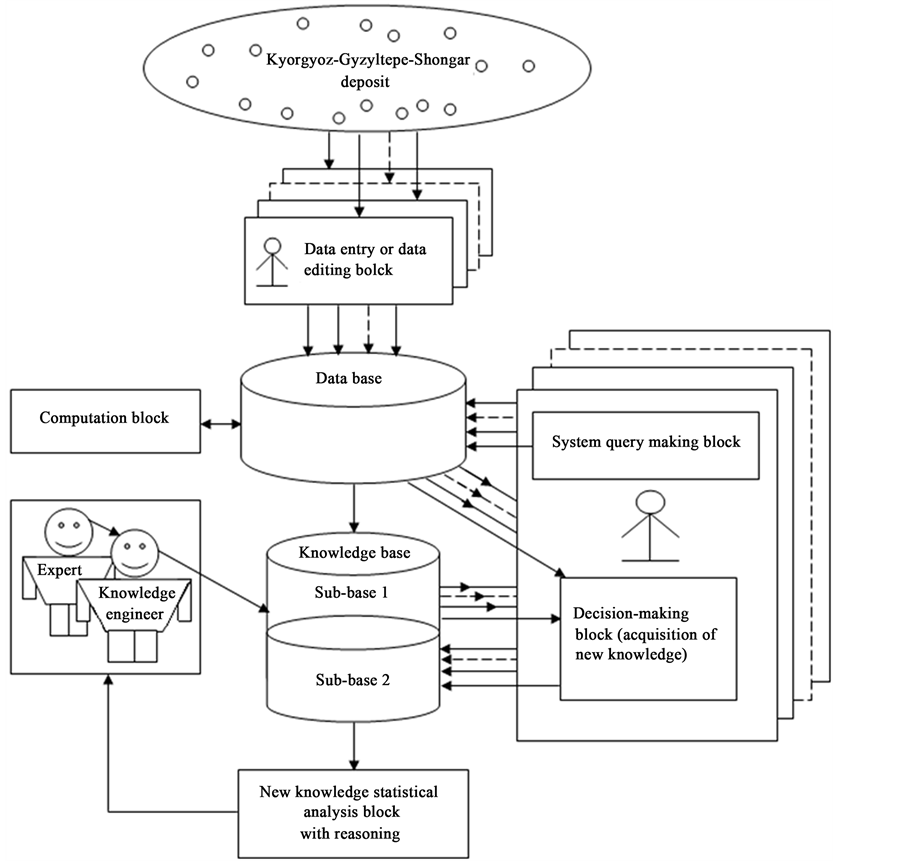
A logical model of IEAS is shown in Figure 1.
Figure 1. Logical model of IEAS.
The proposed IEAS is planned to be used in the Intranet network. Let us trace the operation of the system in Intranet environment. The initial geophysical information from client computers can be entered in the system both for an individual well and in batch mode for a group of wells simultaneously in “input and well editing blocks”. The initial data is subjected to information processing in relational database [6] [7] and prepared for entering the knowledge base (KB) of the system, which we have created in the form of two sub-bases: sub-base 1 and sub-base 2.
A logical model is employed in the system with the purpose of representing expert knowledge generating sub-base 1 of KB together with current facts from the database. Among the ways of application of expert rules, a reverse logical conclusion [8] is used due to its higher efficiency. Presented below is the application domain knowledge in the form of the first-order predicates with the object of subsequent automation of logical conclu- sion. Let us introduce unary predicates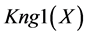
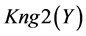
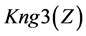
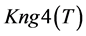
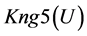
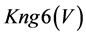
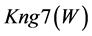
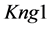
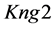
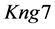
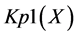
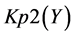
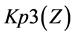
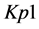
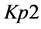
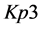
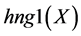
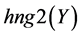
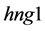
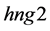
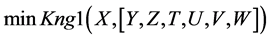
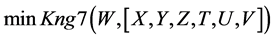
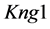
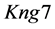
So, in predicate form, logical premises can be represented as follows:
Premise of Rule 1:
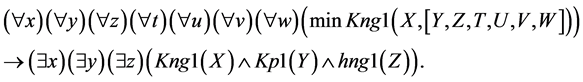
Premise of Rule 2:
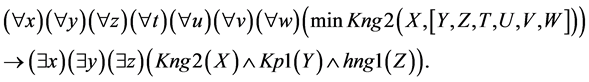
Premises of Rule 3-7 are constructed similarly.
Premise of fact 8:
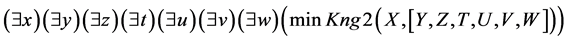
Then logical conclusion can be represented in the following way:
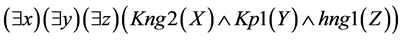
Let us prove by Robinson’s resolution method that a conclusion formula logically follows from a set of pre- mise formulas (See Appendix).
For developing IEAS program, the environment of logical programming Visual Prolog (computer realization of resolution method) was selected.
The making of preferential decisions, which represent vectors (VPD) consisting of three components: oil-and- gas saturation coefficients, porosity coefficients and effective oil-and-gas saturated stratum thickness for an ob- ject of a deposit, takes place at the first stage in the “decision-making” block with the help of logical conclusion mechanism that uses rules and facts of database on the strength of logic of the first-order predicates. A horizon, a block or a well can serve as an object of a deposit.
At the second stage, the adoption of finite decision vectors (FDV) with the participation experts takes place. These vectors can coincide with the said VPD or differ from them in some or other aspects. FDV are accompa- nied by explanations which among other factors may also imply intuition. “Decision making” blocks play a role of blocks of new knowledge acquisition as well. The adopted finite-decision vectors, being essentially new knowledge (facts), constitute the content of KB (knowledge base) sub-base 2.
When developing this IEAS it is also intended to reveal the most significant subset of database rules or, in the final analysis, the most significant subset of alternative methods for the determination of required coefficients. To accomplish this task, the frequency of use of specific FDV is formulated. During each process of making fi- nite decision the statistical frequencies of calls to deposit objects of the following types: a horizon, a block or a well are computed in the “decision-making” block (“new knowledge acquisition”) in real-time mode as the ratio between the quantity of calls to the given object and the total quantity of calls to objects of the given type.
Figure 2 demonstrates the results of calls to specific deposit objects with the use of hierarchical tree.
Figure 2. Hierarchical tree’s fragment of frequency of use of objects.
As seen from Figure 2:
ü hierarchy of tree nodes determines the type of deposit objects selected by user, in the capacity of which can be a horizon, a block or an individual well;
ü horizon IV with frequency of 0.58 turned out to be most frequently selected object of the objects belonging to “horizon” type.
FDVs from each user of IEAS are accumulated in “sub-base 2” of knowledge base, forming new knowledge. This knowledge is analyzed in the statistical analysis of new knowledge with conclusions block in real-time mode to identify the most frequently used rules of knowledge base—the most significant subset of methods for determining the coefficients that can be useful for refining expert knowledge and during the expansion of the system for subsequent deposit (in the course of generation of knowledge base rules for additional ES).
So, the knowledge base of the system is a dynamically updated or variable knowledge base in which know- ledge is continuously corrected as the system is used. In the process of IEAS testing at the deposit objects throughout 2013, the statistical frequencies of FDV [10] [11] were obtained. They are given in Table 1.
FDV 1 in this table stands for decision vector based on rule 1, …, FDV 7-means decision vector based on rule 7. The consistency of the results of experts’ work is assessed by the program using concordance coefficient W, which is calculated according to Kendal’s formula [12] :
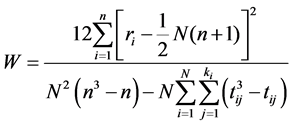
where: n is the number of FDV (n = 7);
N is the number of experts (in IES prototype − N = 5);
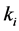
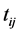
Table 1. Statistical frequencies of decision vectors.
4. Conclusion
Euristic rules have been formed, which comprise the core of a two-component knowledge base consisting of sub-base 1—the totality of rules (backward chaining) and current facts from the database, and sub-base 2 built from new knowledge formed on the basis of the mechanism of Robinson’s resolution first-order predicate logic from the knowledge of sub-base 1. The developed system is a network program using client/server architecture, which reduced the impact of the human factor on the end result. The results of implementation of the prototype system at the Research and Design Institute of SOCAR have proved the serviceability and demonstrated suffi- cient efficiency of the system.
Acknowledgements
This knowledge is analyzed in the Statistical analysis of new knowledge with conclusions block in real-time mode to identify the most frequently used rules of knowledge base—the most significant subset of methods for determining the coefficients that can be useful for refining expert knowledge and during the expansion of the system for subsequent deposit (in the course of generation of knowledge base rules for additional ES).
References
- Mamedov, A.U. and Nagiyev, V.A. (2008) Method of Prediction of Strata Oil-Bearing Capacity. Azerbaijani Oil Facilities, 6, 6-9.
- Nesterova, G.V. and Surodina, I.V. (2008) Interpretation of Charts of Probes of VIKIZ and BKZ on the Basis of Two- Dimensional Mathematical Modeling. http://geology.org.by
- Jakovlev, V.M. http://www.isolne-gis.ru
- Belov, D.L., Chastikov, A.P. and Gavrilova, T.A. (2003) Development of Expert Systems. CLIPS Environment. BHV, Peterburg, 608 p.
- Gavrilova, T.A. and Khoroshevsky, V.F. (2001) Knowledge Bases of Intelligent Systems. SPb: Piter, 384 p.
- Abdullayeva, G.G. and Ismayilov, I.A. (2009) Expert System of the Choice and Decision-Making in Geophysical Re- searches. Transactions of Azerbaijan National Academy of Sciences. Series of Physical-Technical and Mathematical Sciences. Informatics and Control Problems, 24, 134-140.
- Ismayilov, I.A. (2011) Integrated Expert System of Decision-Making on the Example of the Oil and Gas Field. Trans- actions of Azerbaijan National Academy of Sciences. Series of Physical-Technical and Mathematical Sciences. Infor- matics and Control Problems, 26, 154-163.
- Jackson, P. (2001) Introduction to Expert Systems. West Group, Addison-Wesley, Rochester.
- Russel, S.J. and Norvig, P. (1995) Artificial Intelligence: A Modern Approach. Prentice-Hall, Upper Saddle River.
- Nusratov, O.G., Abdullayeva, G.G. and Ismayilov, I.A. (2011) Development of the Integrated Expert Systems of Deci- sion-Making for Tasks of Oil and Gas Fields. Transactions of Azerbaijan National Academy of Sciences. Series of Physical-Technical and Mathematical Sciences. Informatics and Control Problems, 26, 99-105.
- Nusratov, O.G., Abdullayeva, G.G. and Ismayilov, I.A. (2012) Integrated Expert System of Decision Making for Esti- mating Collector Properties and Oil-and-Gas Saturation of Strata. 4th International Conference “Problems of Cybernetics and Informatics”, Baku, 12-14 September 2012, 157-160.
- Kendall, M.G. and Babington Smith, B. (1939) The Problem of m Rankings. The Annals of Mathematical Statistics, 10, 275-287. http://dx.doi.org/10.1214/aoms/1177732186
Appendix
To this end, we shall add “conclusion negation” to a set of premise formulas, then, having excluded an implica- tion sign we shall have the following:
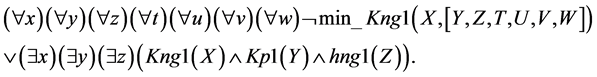
Let us rename the bound variables so that each variable bound by this quantifier would get a unique name in the domain of action of each quantifier and move all quantifiers to the beginning of the formula:
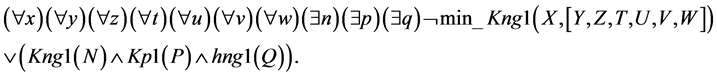
Let us apply the distributive law to the obtained formula
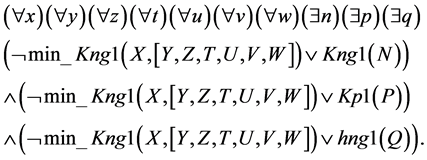
Let us exclude all quantifiers of existence with the help of Skolemization process [9] and omit all quantifiers of generality.
As a result, we have obtained the following conjunctive normal form (CNF) of the initial first premise of ex- perts:
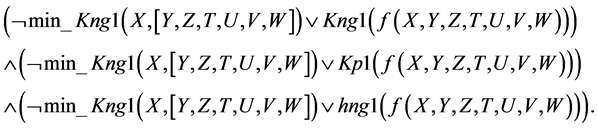
Similar transformations are made to obtain CNF for other premises. Let us proceed to the premise of fact
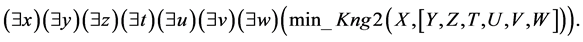
Having omitted all quantifiers of existence after substituting them with subject constants: 
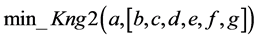
As a result of the above-listed operations, we shall get a set of disjuncts given below in consise form:
1.
2.
3.
……………………………………………………….
19.
20.
21.
22.
Let us prove that from a set of disjuncts (1)-(22) follows the logical conclusion:
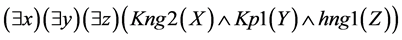
For proving by resolution method, we shall apply a logical negation operation to Formula (15) (conclusion), transfer the negation sign inside the formula, substituting the existence quantifiers with generality quantifiers. Further, having applied De Morgan’s law to the formula and omitted generality quantifiers, we shall have the following (CNF):
23.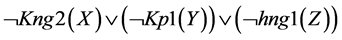
Let us add it to the set of premises and prove the inconsistency of the obtained set of Formulas (1)-(23). Ac- cording to Robinson’s resolution method, the product of sums must be unsatisfiable. From the set of disjunctions
(4)-(6) and (22) by means of substituting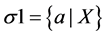
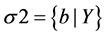
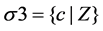
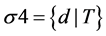
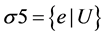
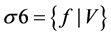
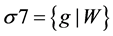
24.
In turn, when substituting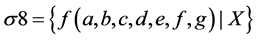
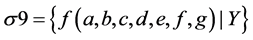
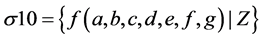
Hence, the inconsistency or unsatisfiability of conjunction of the formulas of the initial set of premises and negation of conclusion is proved, which confirms trueness of the logical conclusion.