Intelligent Control and Automation
Vol.4 No.4(2013), Article ID:39502,8 pages DOI:10.4236/ica.2013.44044
Evolutionary Techniques for Reverse Auctions
Department of Computer Science, University of Regina, Regina, Canada
Email: shil200s@uregina.ca, sadaouis@uregina.ca, mouhoubm@uregina.ca
Copyright © 2013 Shubhashis Kumar Shil et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 22, 2013; revised September 22, 2013; accepted September 30, 2013
Keywords: Winner Determination; Combinatorial Reverse Auctions; Genetic Algorithms
ABSTRACT
Winner determination is one of the main challenges in combinatorial auctions. However, not much work has been done to solve this problem in the case of reverse auctions using evolutionary techniques. This has motivated us to propose an improvement of a genetic algorithm based method, we have previously proposed, to address two important issues in the context of combinatorial reverse auctions: determining the winner(s) in a reasonable processing time, and reducing the procurement cost. In order to evaluate the performance of our proposed method in practice, we conduct several experiments on combinatorial reverse auctions instances. The results we report in this paper clearly demonstrate the efficiency of our new method in terms of processing time and procurement cost.
1. Introduction
An auction is a market place where the bidders compete for item(s). In a traditional or standard auction, an item is auctioned separately, which leads to an inefficient allocation and processing time [1,2]. To improve the efficiency of bid allocation, combinatorial auctions have been proposed by allowing bidders to bid on multiple items [1,3]. This type of auctions provides a combinatorial allocation that minimizes the procurement cost and processing time [1,2,4]. Combinatorial auctions have been used to solve many real-world applications [5] such as supply chain management [6], resource allocation with real-time constraints [2], computer grids [7], and sensor management [3,8]. A combinatorial auction problem has been demonstrated as a winner determination problem [9]. Winner determination is still one of the main challenges of combinatorial auctions [2]. Indeed, determining the winner(s) in combinatorial auctions is an extremely complex problem that has been shown to be NP-complete [1,4]. On the other hand, applying combinatorial auctions to procurement scenarios [10,11], such as travel packages and transportation services, may save the costs [1]. Several methods have been proposed to solve combinatorial auction problems [1]. Some research works have been carried out to determine the efficient way to solve the winner determination problem in combinatorial auctions. Most of the proposed methods limit the bundles on which bids can be submitted in order to solve the problem optimally, but this type of restrictions introduces economic inefficiencies [1]. Some other techniques avoid these restrictions but allow bidding on a small number of items [1].
In this paper, we are interested in combinatorial reverse auctions in which we consider the procurement of a single unit of multiple items. In our auction, there is one buyer and several sellers who compete according to the buyer’s requirements. First, the buyer announces his demand (multiple items) in the auction system. Then, the interested sellers register for that auction and bid on a combination of items. Genetic Algorithms (GAs) were successful to solve many combinatorial optimization problems [1], such as quadratic assignment problem [12], travelling salesman problem [13] and job scheduling [14]. Nevertheless, not much work has been done by using GAs to solve the winner determination problem in the context of combinatorial reverse auctions. In [15,16], we have proposed a GA based method that we called GACRA (Genetic Algorithm for Combinatorial Reverse Auctions) to tackle this problem. GACRA is successful in finding optimal solutions; however, it needs comparatively a considerable amount of time to produce good solutions as it uses two repairing methods. Our research goal here is twofold: 1) solve the winner determination problem in combinatorial reverse auctions in a reasonable processing time, and 2) reduce the procurement cost with fewer generations. For this purpose, we improve the method GACRA described in [15,16] and name our new method Improved Genetic Algorithms for Combinatorial Reverse Auctions (IGACRA). IGACRA only uses one repairing function to repair infeasible chromosomes. Moreover, we conduct several experiments by comparing IGACRA with GACRA for finding the winner(s) in combinatorial reverse auctions. The experimental results we report here clearly demonstrate the superiority of IGACRA in terms of processing time and procurement cost. In addition, some statistical measurements reveal that IGACRA is a consistent method.
The rest of the paper is organized as follows. In Section 2, the literature related to this research work is discussed with a focus on winner determination and genetic algorithms, and briefly outlines how GACRA is used in [15,16] to address the winner determination problem. In Section 3, the proposed IGACRA is presented in detail through an example. In Section 4, the experimental study we have conducted to evaluate the running time and procurement cost of our method is reported. Finally, concluding remarks and future research directions are listed in Section 5.
2. Background
2.1. Winner Determination
Winner determination in combinatorial auctions is computationally expensive and has been classified as a NPcomplete problem [1,4]. In practice, the following three approaches have been adopted to tackle this problem [4]: the first one is to limit the allowable bids, the second one is to address the unrestricted problems using search techniques, and the last one is to find a sub-optimal allocation.
Winner determination is based on two parts [5]: satisfiability and optimization. The main target of satisfiability is to find a solution to a given problem satisfying a set of required services. On the other hand, the basic task of optimization is to find the winner(s) based on multiple criteria [5], such as reduced procurement cost and processing time. The required services identified to solve a task at the optimum measurement are the winners. The relationship between services can be of three types such as co-operation, benefit co-operation and no co-operation. The order in which these services are combined in all the three relationships according to the criteria used for optimization is important [5].
2.2. Genetic Algorithms
GAs are powerful search techniques consisting of selection, crossover and mutation methods that follow the Darwinian principle of survival: “Survival is the fittest” [17]. They are considered as approximate search algorithms driven by genetics and natural selection [18]. GAs algorithms model the sexual reproduction [19]. They are stochastic and polynomial rather than exponential [2] and are often used as an alternative approach for solving hard problems. The crossover operator builds a child with the combined characteristics of its parents. In contrast, mutation is a unary operator that needs only one input. During the process, the mutation operator produces a child by selecting some bad genes from the parent and replacing them with the good genes. Crossover and mutation both follow the characteristic of GAs in that the next generation is expected to perform better than the current one. GAs can terminate anytime as required and the current best chromosome can be the best solution within the required running time; that is why it is called anytime algorithm [5]. We may note that the problem representation is one of the most challenging tasks to the success of GAs [5]. Determining an appropriate fitness function for a specific problem is another crucial part of GAs in which the qualities of chromosomes are assessed, and very often this task requires most CPU intensive part of GAs [4].
Genetic Algorithms (GAs) perform iterative multi-directional non systematic searches by maintaining a constant size population of individuals and encouraging information generation and exchange between these directions [20]. Each iteration is called a generation and it undergoes some changes through crossover and mutation operators [20]. At each generation, good solutions are expected to be produced and bad solutions die. It is the role of the fitness function to distinguish the goodness of the solution [20].
2.3. Genetic Algorithms in Combinatorial Reverse Auctions
Combinatorial auctions provide a more efficient allocation than standard auctions in a multi-item scenario [1,2,4]. In [15,16], we have used GAs to solve the winner determination problem in the context of combinatorial reverse auctions. In our proposed GACRA method [15,16], infeasible chromosomes are repaired by removing redundancy and emptiness through two repairing methods. Emptiness means a chromosome in which some item(s) are not selected, while in redundancy some item(s) are chosen more than once. Moreover, the gamblingwheel disk selection method has been adapted to choose the chromosome for the crossover operation. Then in the crossover operation, the modified two-point crossover operator has been used. Regarding the mutation operation, the product configuration of two different suppliers was interchanged in the same chromosome. The population size has been set to 100, the crossover probability to 60%, and the mutation rate to 1%.
3. Proposed GA-Based Method
In Figure 1, a combinatorial reverse auction scenario is depicted. The buyer wants to buy items A and B. Three sellers are bidding with many feasible solutions. For example, seller 1 provides both items A and B, seller 2 item B and seller 3 item A, etc. Winner(s) will be selected based on the minimum bid price. In real life, the running time for finding the optimal solution is also considered.
In Algorithm 1, we define our proposed Improved Genetic Algorithms for Combinatorial Reverse Auctions (IGACRA) method. Assume there are m items and n sellers. In this case, the number of bid items combinations is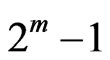 . The target of winner determination in combinatorial reverse auctions is to reduce the procurement cost. Let us consider an example with n = 3 (sellers S1, S2 and S3) and m = 2 (items A and B). Assume there are six chromosomes in each generation for this example. We use m × n bits to represent each chromosome, so in this case, 2 × 3 = 6 bits are used for each chromosome.
. The target of winner determination in combinatorial reverse auctions is to reduce the procurement cost. Let us consider an example with n = 3 (sellers S1, S2 and S3) and m = 2 (items A and B). Assume there are six chromosomes in each generation for this example. We use m × n bits to represent each chromosome, so in this case, 2 × 3 = 6 bits are used for each chromosome.

In this particular case, the total number of possible combination of bid items for each seller is . The item combinations are:
. The item combinations are:
• Bidding for only item A = {A} = {10}
• Bidding for only item B = {B} = {01}
• Bidding for both items A and B = {A, B} = {11}.
Here, in the procedure of chromosome encoding, the corresponding bit is assigned to 1 if the seller bids for that item, and 0 otherwise. Let us consider the chromosome 100100. The first two bits (10) are for seller S1, the next two bits (01) for S2, and the last two bits (00) for S3.In other words, this means that seller S1 bids only for item A, S2 bids for only item B, and S3 does not bid for any item.
Through the above example, we describe in the following the steps of IGACRA. We use one repairing function named repair Chromosome rather than using two repairing functions named Remove Redundancy and Remove Emptiness as in [15,16]. We also employ the two-point crossover operator defined in [14] in lieu of our former proposed modified two-point crossover operator [15,16].
Steps 1-3
To generate bid prices, we consider random values between 200 and 500 for each item and for each seller. In Step 2, the bid Generator function performs this task. In Step 3, chromosome Generator function generates the chromosomes. For example, the six initial chromosomes are generated randomly by selecting a bid for each seller from the item combinations in the interval of [1, 2m]. A particular case is when 2m is chosen (in our example 22 = 4). This means no item is selected for bidding for the
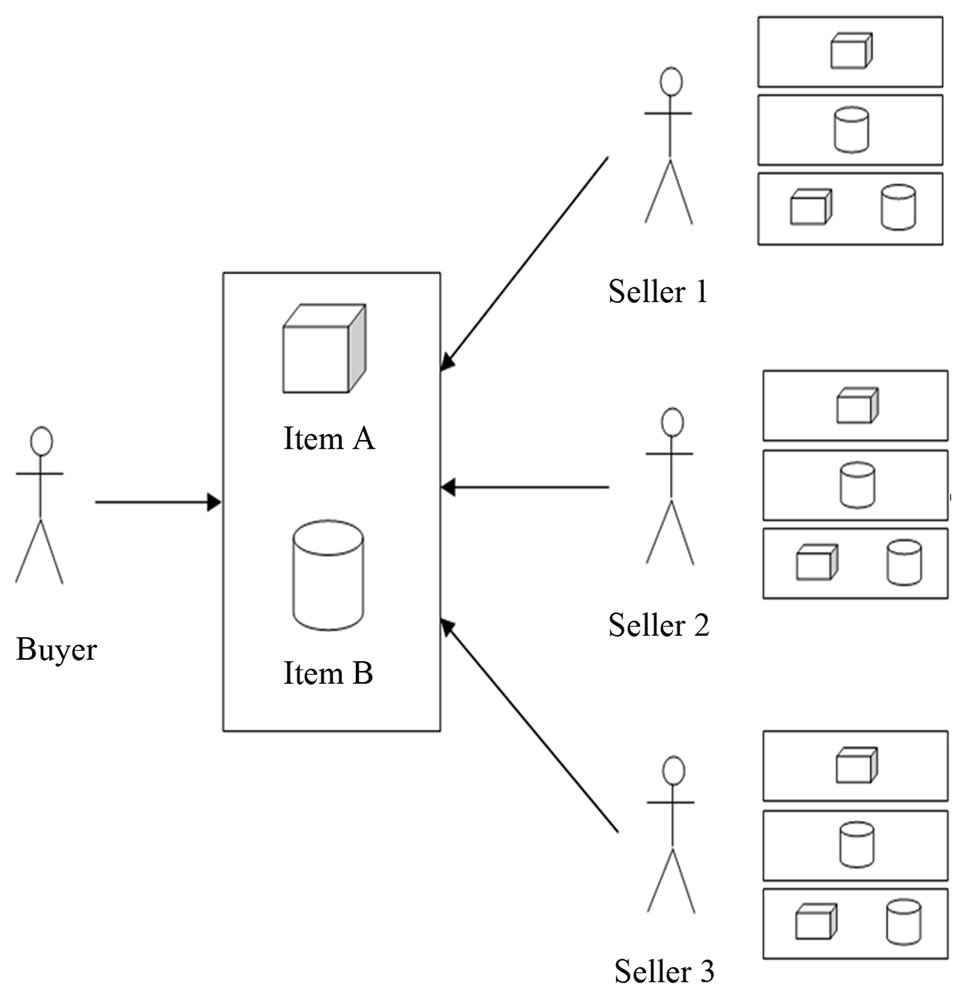
Figure 1. A combinatorial reverse auction scenario.
seller, so the corresponding bid item combination is {00} and the price is also 0.
Steps 4-5
To repair infeasible chromosomes, the repair Chromosome() method, defined in Algorithm 2, ensures exactly one selection of every item from all sellers in each chromosome. So, we repair infeasible chromosomes by using this method. Repair Chromosome() has four functions: is Feasible(), assign Zeros(), generate Random() and assign One(). The task of is Feasible() is to return true if the chromosome has exactly one selection of every item from all sellers and false otherwise. This function uses the XOR operation to find it out. The task of assign Zeros() is to assign 0s to all the bits of an infeasible chromosome. The task of generate Random() is to return a random number between 1 and n. The task of assign One() is to assign 1 to the particular bit of an infeasible chromosome generated by the generate Random() function.
Let us consider the following example to illustrate our repairChromosome method. Assume the chromosome is 001101. For this chromosome, the first two bits (00) are for seller S1, the next two bits (11) for S2, and the last two bits (01) for S3. Moreover, the first, third and fifth bits are for item A and the second, fourth and sixth bits are for item B. The is Feasible() function performs XOR operations between the bits of item A and then between the bits of item B. For item A, it finds exactly one selection. However, for item B it finds more than one selection and therefore returns false which means the chromosome is infeasible. Then assign Zero() converts the chromosomes into 000000 generate Random() generates random value between 1 and 3 for each item. Assume 1 is generated for item A and 3 for item B. assign One() assigns 1 to the bit for item A in the position for S1 and 1 to the bit for item B in the position for S3. Thus, the chromosome is converted into 100001 which is feasible. Table 1 lists the initial chromosomes after repairing.
In step 5, chromosome fitness value is computed by the fitness Chromosome function. Since the motivation of this research work is to minimize the procurement cost for the buyer, our fitness function for a given Xi is defined as follows,
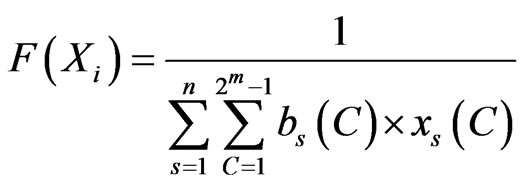
where
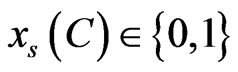 (1)
(1)
bs (C) represents a bid for the item combination C submitted from the sth seller. xs(C) is 1 when the item combination C is selected for the sth seller and 0 otherwise.
Steps 6-7
The selection Chromosome function uses the gambling-wheel disk selection method [9]. In this selection procedure, at first the sum of fitness values of all chromosomes is calculated, then a corresponding scope located in [0, 1] is assigned to each chromosome according to its fitness value.
For example, if the fitness value of the first chromosome is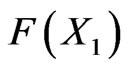 , and the sum of the fitness values of all chromosomes is F, then its corresponding scope is
, and the sum of the fitness values of all chromosomes is F, then its corresponding scope is 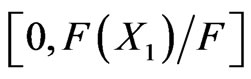 . If the fitness value of the second chromosome is
. If the fitness value of the second chromosome is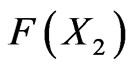 , then its scope is
, then its scope is 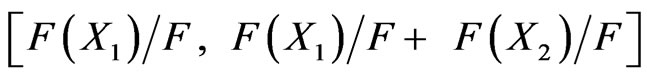 . In this way, we can deduce the scope of all chromosomes as follows.
. In this way, we can deduce the scope of all chromosomes as follows.
 (2)
(2)
The chromosome that has the highest fitness value also has the longest scope which means that it has a better chance to be selected. For each chromosome a random number from [0, 1] is generated. If this number falls in the scope of one chromosome, then that chromosome is selected.
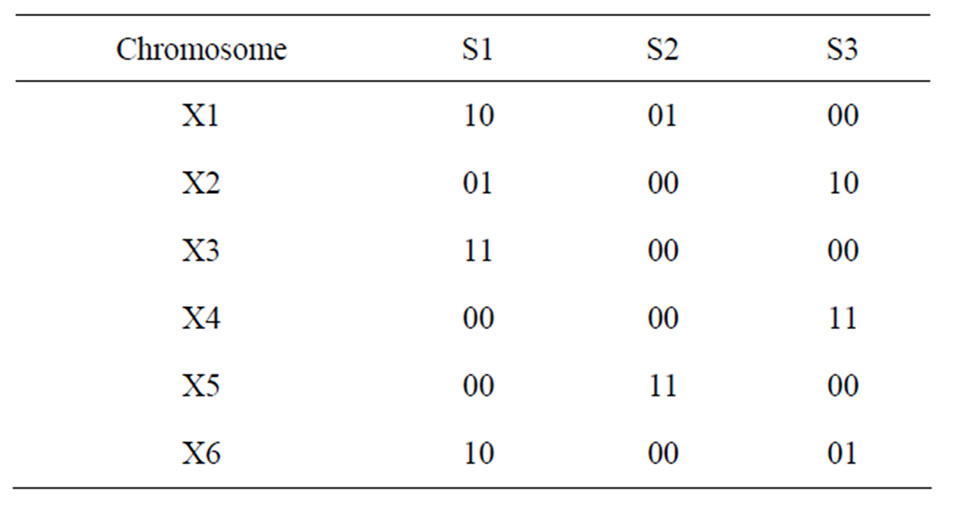
Table 1. Initial chromosomes.
In step 7, the crossover operation is performed using the two-point crossover method. At first the fitness values of the parents are calculated. According to the crossover rate only those parents with a relatively better fitness values are considered for crossover. Figure 2 shows the two-point crossover operation. A child chromosome takes two portions from one parent and one portion from the other parent. In Algorithm 1, crossover Chromosome() function performs this task.
In our algorithm, 60% of the total chromosomes will get the chance to participate in crossover operation. In Figure 2, Xparent3 and Xparent1 participate in crossover operation and Xchild3 and Xchild1 are created.
Steps 8-12
The procedure will move to mutation operation as indicated in our algorithm. In this step chromosomes are selected randomly and item combinations between two sellers are altered. Figure 3 shows a given mutation operation.
Assume X2 chromosome is selected randomly for mutation operation. S1 and S3 sellers are selected randomly and their bid combinations are altered. Finally
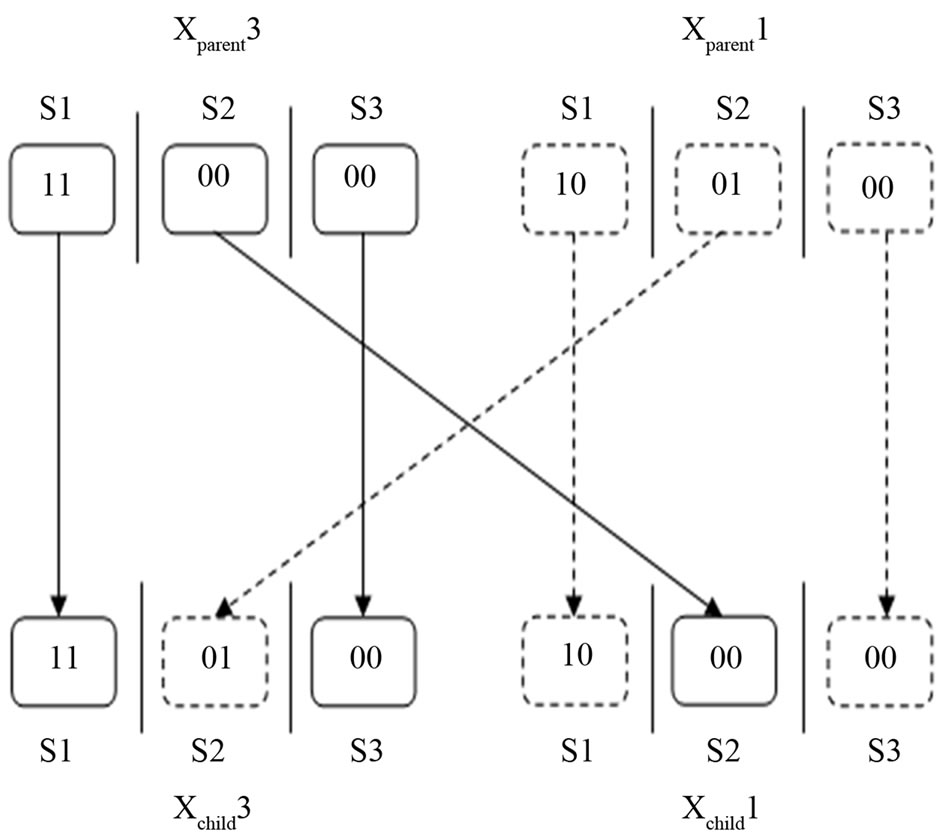
Figure 2. Two-point crossover operation.
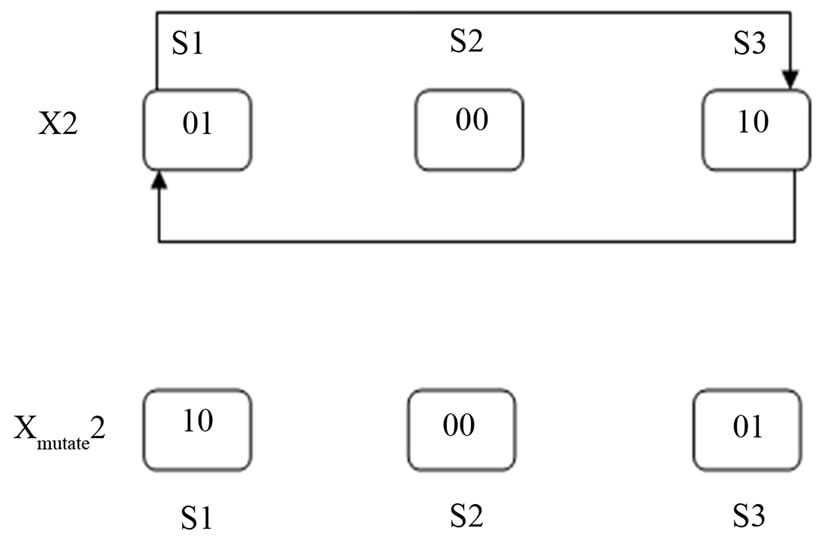
Figure 3. Mutation operation.
Xmutate2 is created. The mutation Chromosome() function performs this task.
In step 9, repair Chromosome() repairs the infeasible chromosomes. In step 10, our fitness function calculates the fitness values of the chromosomes.
In step 11, the procedure selects the better chromosomes among the initial and new chromosomes of the generation by using the new Chromosome Generator() function. Since a genetic algorithm is an anytime algorithm, our procedure can be stopped anytime and produces the best solution so far. The entire process is repeated until the termination condition is fulfilled, which in our case is the number of generations. In step 12, after fulfilling the termination condition the procedure returns the winner(s). While the solution is not improving in every generation, we always preserve the current winner.
4. Experimentation
We conduct in this paper several experiments to solve the winner determination problem in combinatorial reverse auctions using IGACRA. The goal of the experiments is to evaluate the performance of IGACRA in terms of running time and procurement cost. We also compare IGACRA with our former method GACRA [15,16].
Both IGACRA and GACRA are coded in Java and executed on an AMD Athlon (tm) 64 X2 Dual Core Processor 4400+ with 3.43 GB of RAM and 2.30 GHz of processor speed. We utilize the following common parameters and settings for all the experiments.
• Chromosome Encoding: Binary String
• Number of Chromosome: 100
• Selection: Gambling-Wheel Disk
• Crossover: Two-point
• Crossover Rate: 0.6
• Mutation Rate: 0.01
• Termination Condition: Generation Number
We evaluate our proposed procedure through the following experiments:
1) At first we compare our procedure with GACRAwith respect to both bid price and running time.
2) We test our procedure measuring running time by varying the number of items and number of sellers.
3) We analyze the IGACRA consistency through some statistical measurements.
Experiment 1
In this first experiment, we measure the required time of our proposed method and then compare it with GACRA.
In Figure 4, we show the required time (in milliseconds) versus the number of generations for both IGACRA and GACRA. This is the average required time of 20 runs. In this experiment 20 sellers compete for 5 items.
From the comparison we can see that IGACRA needs less processing time. This happens because of using one and simple repairing function rather than two functions [15,16].
Experiment 2
We also conduct experiments on the procurement cost and report the average results of 20 runs in Figure 5. For 5 items, 20 sellers compete in this experiment. The price of each item is between 200 and 500. Bid price versus number of generations is shown for both IGACRA and GACRA.
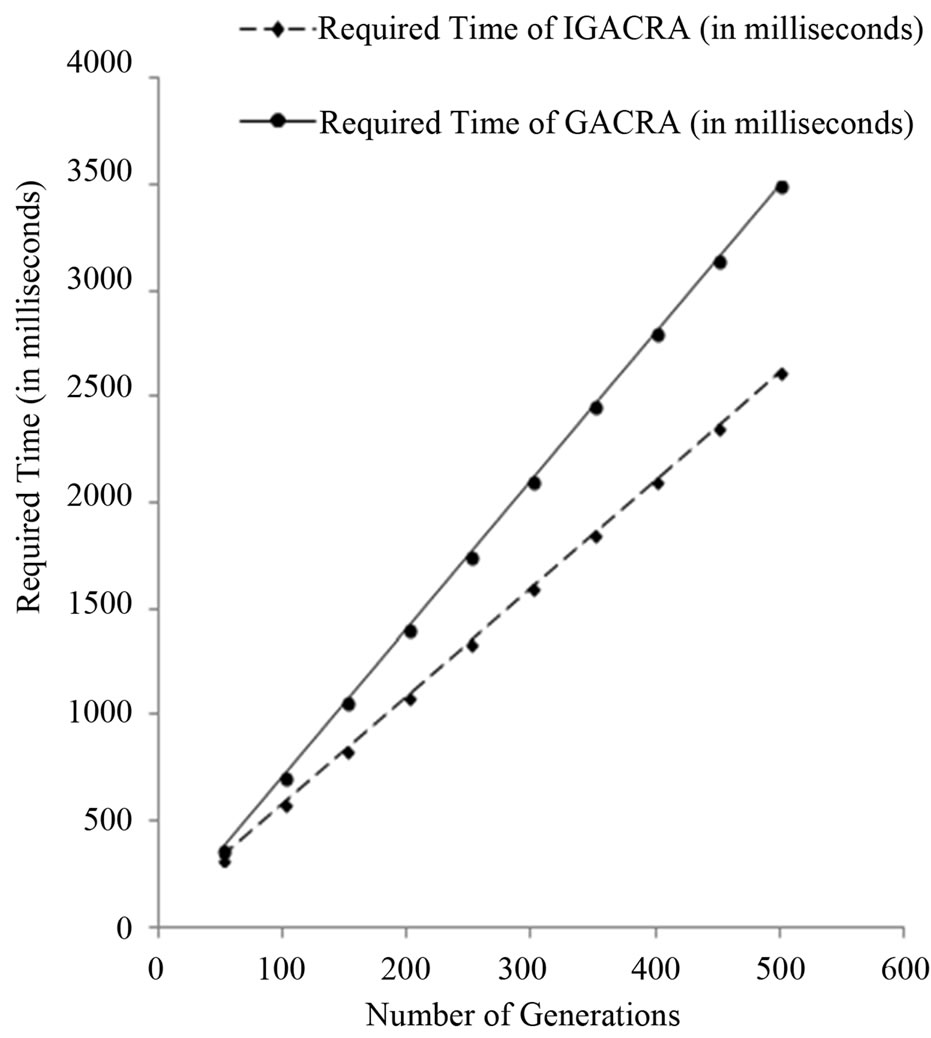
Figure 4. Required time vs number of generations.
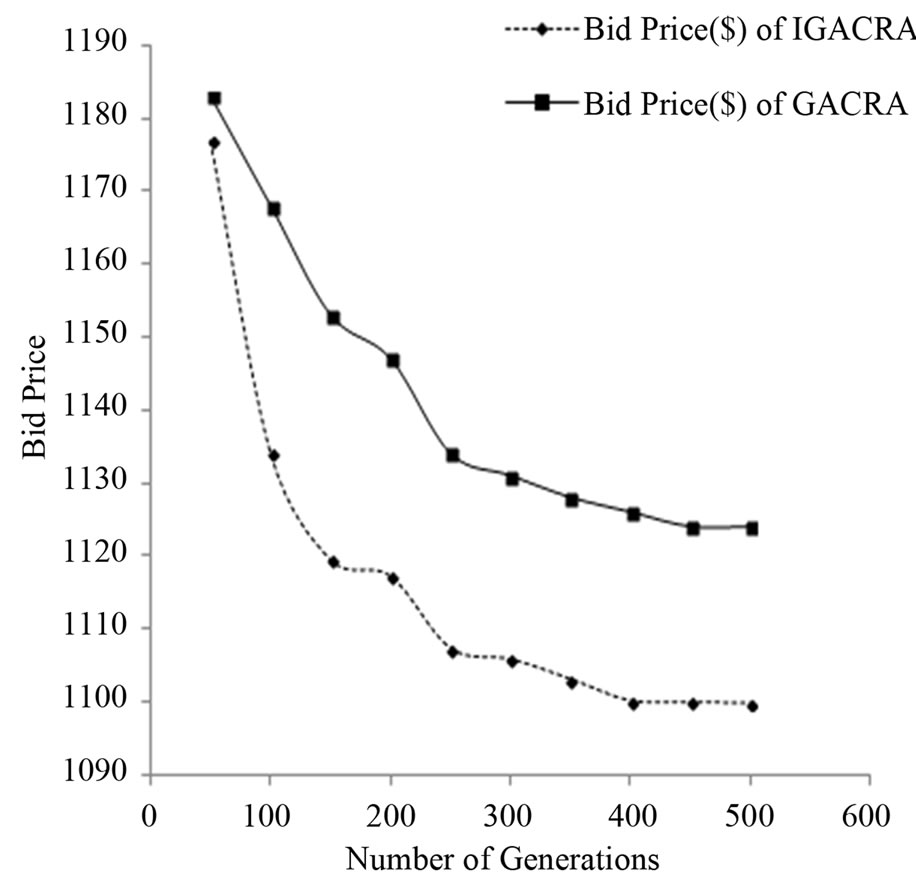
Figure 5. Bid price vs number of generations.
Since our procedure always maintains feasible solutions and never accepts more than one instance of a specific bid item, it is able to produce good solutions from the very first generations. Moreover, it keeps producing better solutions in the consecutive generations.
Experiment 3
In Figure 6, we show the average bid price of 20 runs for IGACRA with the maximum and minimum values indicated by ‘+’ and ‘−’ respectively and error bars with confidence level of 95%. This experiment is based on the results found in experiment 2.
The solid line represents the average bid price and the error bars indicate 95% confidence level. The data points above and below the error bars show the maximum and minimum bid prices found over 20 runs.
Clearly IGACRA gives consistently a better solution quality. It should also be noted that the solution quality increases steadily over generations. We also notice that the variability of the solution quality over multiple runs improves over the generations. Together with the fact that the minimum bid price remains constant, this suggests that the best solution found by IGACRA might be the optimal solution to the problem.
Overall, these observations illustrate the any-time behavior and more importantly the consistency of the IGACRA algorithm. IGACRA is able to minimize the procurement cost from the very early generations. Therefore, in the real world scenario, IGACRA is appropriate to produce minimum bid price when the allowable processing time is too short.
Experiment 4
In this experiment, we assess the processing time for

Figure 6. Bid price vs number of generations with error bars of IGACRA.
IGACRA by varying the number of sellers and keeping the number of items fixed to 2, 4, 6 and 8. Figure 7 illustrates the required time (in seconds) versus the number of sellers. For this experiment 100 generations is used as the termination condition.
This running time increases with the increment of the number of sellers. For a higher number of items, this increment occurs more sharply because of encoding more bits for chromosomes, calculating fitness values and operating on more chromosomes.
Experiment 5
We also report the results of experiments in terms of running time obtained by varying the number of items and keeping the number of sellers fixed to 20, 40, 60 and 80. In Figure 8, the required time (in seconds) versus the number of items is shown. For this experiment, 100 generations are used as the termination condition.
These results also demonstrate that with the increase of the number of items, the required time increases and for a higher number of sellers it increases more sharply as for the same reason of increasing items.
The number of bits required to represent the chromosomes in IGACRA directly depends on both the number of items and the number of sellers. Therefore increasing any of these will increase the number of bits in the chromosomes which will increase the required running time.
5. Conclusion and Future Work
Motivated to reduce both the processing time and the
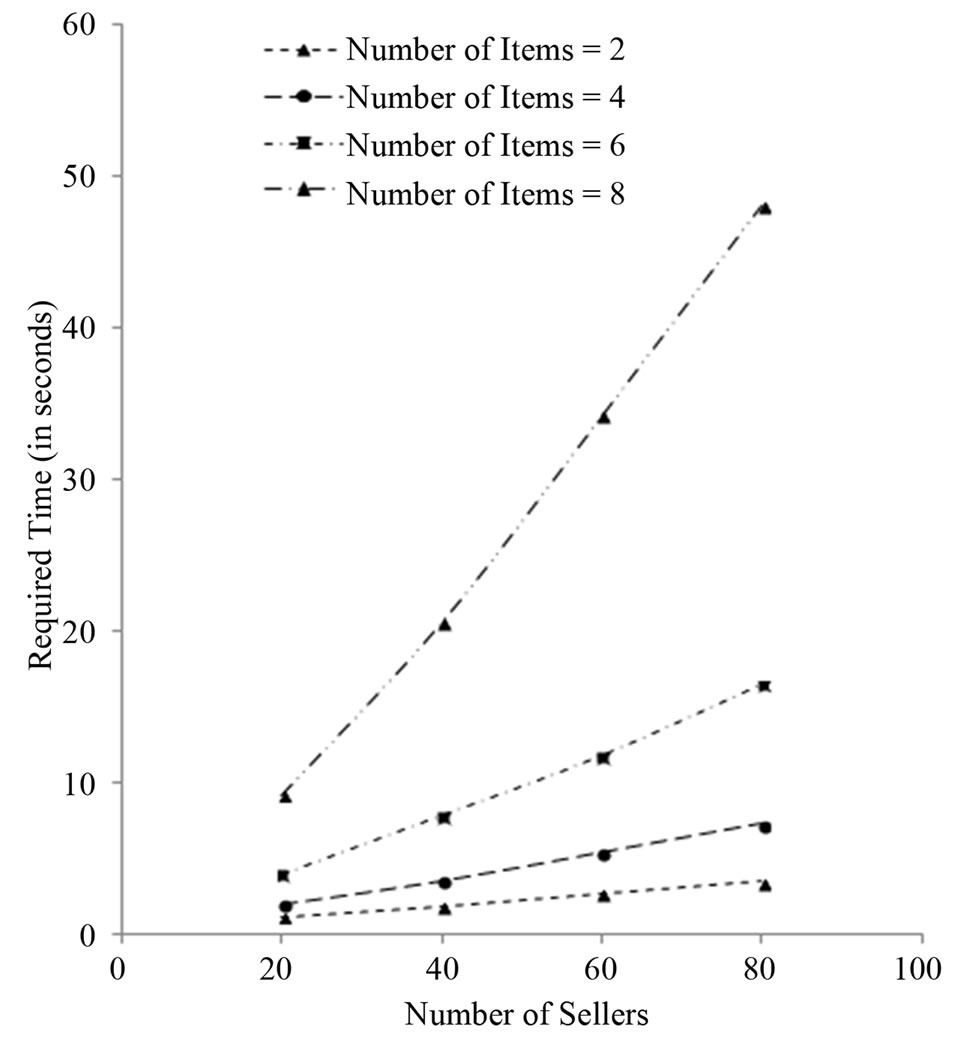
Figure 7. Required time vs number of sellers.
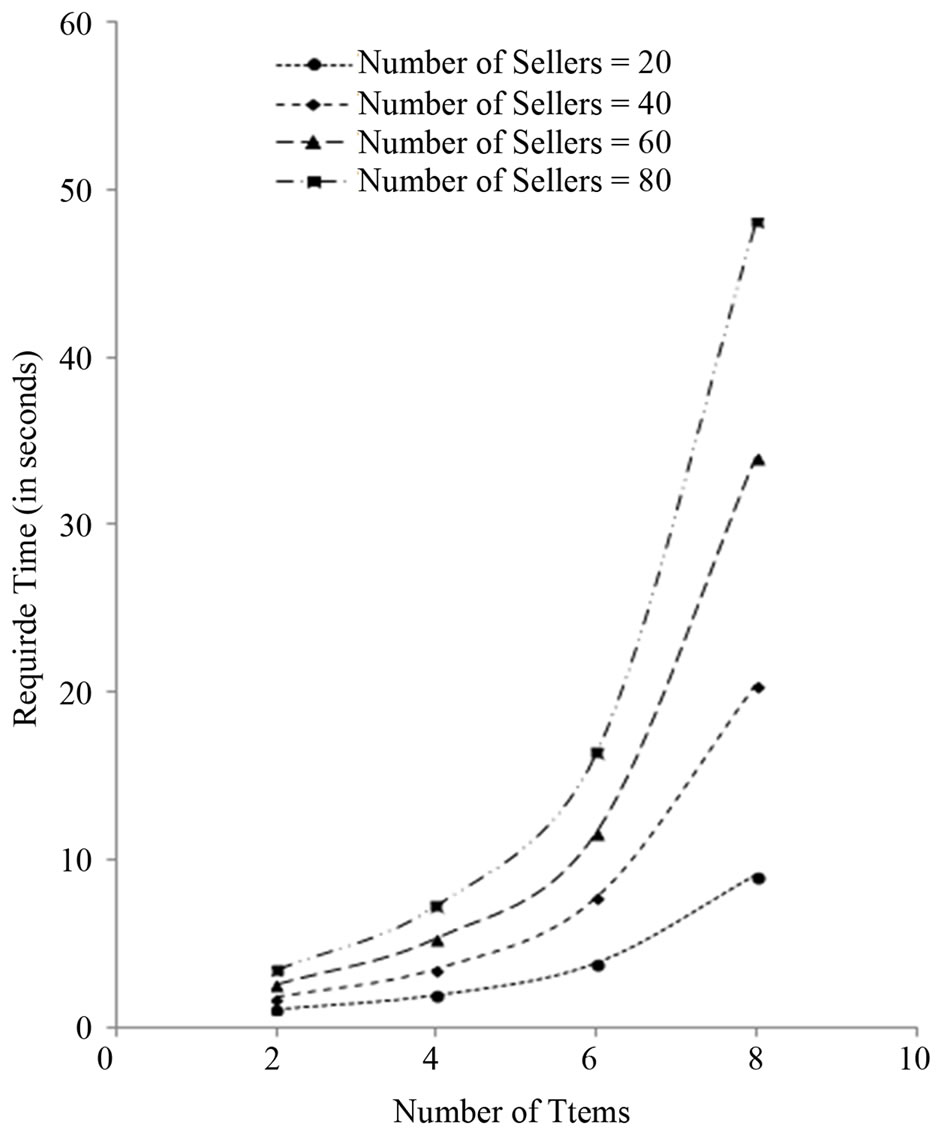
Figure 8. Required time vs number of items.
procurement cost, this research work addresses the problem of winner determination in combinatorial reverse auctions.
Indeed, every important operation of the proposed GA-based method is chosen very carefully along with some other fruitful mechanisms in each step. We define the repairing method, repair Chromosome(), to ensure feasible solutions. With the help of this repairing method and a careful selection of genetic algorithms operators, it is notable that our method can produce optimal solutions in a reduced processing time in the context of combinatorial reverse auctions.
Real-time response to large-scale applications is needed in resource allocation and e-commerce areas [21]. When the solutions should be produced quickly for large problem instances, exact algorithms are not only inadequate but also infeasible [21]. Furthermore, in real life, certain domains may need approximate solutions within a suitable processing time [21]. For these reasons, in this research we consider GAs to solve the problem of winner determination and our IGACRA algorithm is able to produce good solutions from the very first generations.
Since parallel GAs are capable of constructing the solutions more efficiently [18,22], the future target of this research is to solve the problem of winner determination in combinatorial reverse auctions by using the parallel GAs. Another future direction is to consider some other non-price dimensions such as warranty, customer rating, and time of delivery.
REFERENCES
- P. Patodi, A. K. Ray and M. Jenamani, “GA Based Winner Determination in Combinatorial Reverse Auction”. Proceedings of the 2nd International Conference on Emerging Applications of Information Technology, Kolkata,19-20 February 2011, pp. 361-364.
- V. Avasarala, H. Polavarapu and T. Mullen, “An Approximate Algorithm for Resource Allocation using Combinatorial Auctions,” Proceeding of the IEEE/WIC/ ACM International Conference on Intelligent Agent Technology, Hong Kong, 18-22 December 2006, pp. 571- 578.
- T. Mullen, V. Avasarala and D. L. Hall, “CustomerDriven Sensor Management,” IEEE Intelligent Systems, Vol. 21, No. 2, 2006, pp. 41-49. http://dx.doi.org/10.1109/MIS.2006.23
- L. Zhang and R. Zhang, “The Winner Determination Approach of Combinatorial Auctions based on Double Layer Orthogonal Multi-Agent Genetic Algorithm”, Proceedings of the 2nd IEEE Conference on Industrial Electronics and Applications, Harbin, 23-25 May 2007, pp. 2382-2386.
- A. M. Easwaran and J. Pitt, “An Agent Service Brokering Algorithm for Winner Determination in Combinatorial Auctions,” Proceedings of the 14th European Conference on Artificial Intelligence, Berlin, 20-25 August 2000, pp. 286-290.
- W. E. Walsh, M. Wellman and F. Ygge, “Combinatorial Auctions for Supply Chain Formation”, Proceeding of the ACM Conference on Electronic Commerce, 2000, pp. 260-269. http://dx.doi.org/10.1145/352871.352900
- A. Das and D. Grosu, “A Combinatorial Auction-Based Protocols for Resource Allocation in Grids,” Proceedings of the 19th IEEE International on Parallel and Distributed Processing Symposium, 4-8 April 2005. http://dx.doi.org/10.1109/IPDPS.2005.140
- V. Avasarala, T. Mullen, D. L. Hall and A. Garga, “MASM: Market Architecture or Sensor Management in Distributed Sensor Networks,” Proceeding of the SPIE Defense and Security Symposium, Vol. 5813, 2005, pp. 281-289.
- J. Gong, J. Qi, G. Xiong, H. Chen and W. Huang, “AGA Based Combinatorial Auction Algorithm for Multi-robot Cooperative Hunting,” Proceedings of theInternational Conference on Computational Intelligence and Security, Harbin, 15-19 December 2007, pp. 137-141.
- S. J. Rassenti, V. L. Smith and R. L. Bulfin, “A Combinatorial Auction Mechanism for Airport Time Slot Allocation,” The Bell Journal of Economics, RAND Corporation, Vol. 13, No. 2, 1982, pp. 402-417. http://dx.doi.org/10.2307/3003463
- Y. Narahari and P. Dayama, “Combinatorial Auctions for Electronic Business,” Sadhana, Vol. 30, No. 2-3, 2005, pp. 179-211. http://dx.doi.org/10.1007/BF02706244
- D. M. Tate and A. E. Smith, “A Genetic Approach to the Quadratic Assignment Problem”, Computers and Operations Research, Vol. 22, No. 1, 1995, pp. 73-83. http://dx.doi.org/10.1016/0305-0548(93)E0020-T
- H. Watabe and T. Kawaoka, “Application of Multi-Step GA to the Travelling Salesman Problem”, Proceedings of the 4th International Conference on Knowledge-Based Intelligent Engineering Systems and Allied Technologies, Vol. 2, Brighton, UK, 30 August-1 September 2000, pp. 510-513.
- P. Senthilkumar and P. Shahabudeen, “GA Based Heuristic for the Open Job Scheduling Problem”, International Journal of Advanced Manufacturing Technology, Vol. 30, No. 3-4, 2006, pp. 297-301. http://dx.doi.org/10.1007/s00170-005-0057-2
- S. K. Shil, M. Mouhoub and S. Sadaoui, “Winner Determination in Combinatorial Reverse Auctions”, In: Contemporary Challenges and Solutions in Applied Artificial Intelligence, Studies in Computational Intelligence, Vol. 489, 2013, pp. 35-40.
- S. K. Shil, M. Mouhoub and S. Sadaoui, “An Approach to Solve Winner Determination in Combinatorial Reverse Auctions Using Genetic Algorithms”, Proceeding of the 15th Annual Conference Companion on Genetic and Evolutionary Computation Conference Companion, Amsterdam, The Netherlands, 6-10 July 2013, pp. 75-76. http://dx.doi.org/10.1145/2464576.2464611
- D. E. Goldberg and K. Deb, “A Comparative Analysis of Selection Schemes Used in Genetic Algorithms”, In: G. J. E. Rawlins, Ed., Foundations of Genetic Algorithms, Morgan Kaufmann, Burlington, 1991, pp. 69-93.
- M. Nowostawski and R. Poli, “Parallel Genetic Algorithm Taxonomy,” Proceedings of the 3rd International Conference on Knowledge-Based Intelligent Information Engineering Systems, Adelaide, December 1999, pp. 88- 92.
- H. Muhlenbein, “Evolution in Time and Space—The Parallel Genetic Algorithm,” In: G. J. E. Rawlins, Ed., Foundations of Genetic Algorithms, Morgan Kaufmann, Burlington, 1991, pp. 316-337.
- M. Mouhoub, “Systematic versus Local Search and GA Techniques for Incremental SAT,” International Journal of Computational Intelligence and Applications, Vol. 7, No. 1, 2008, pp. 77-96. http://dx.doi.org/10.1142/S1469026808002193
- H. H. Hoos and C. Boutilier, “Solving Combinatorial Auctions using Stochastic Local Search,” Proceedings of the 17th National Conference on Artificial Intelligence, Austin, 30 July-3 August 2000, pp. 22-29.
- R. Abbasian and M. Mouhoub, “An Efficient Hierarchical Parallel Genetic Algorithm for Graph Coloring Problem”, Proceedings of the 13th Annual Genetic and Evolutionary Computation Conference, Dublin, 12-16 July 2011, pp. 521-528. http://dx.doi.org/10.1145/2001576.2001648

