Intelligent Control and Automation
Vol. 3 No. 1 (2012) , Article ID: 17571 , 10 pages DOI:10.4236/ica.2012.31005
Delay-Dependent Stability Analysis of Discrete Time Delay Systems with Actuator Saturation
1Department of Electrical Engineering, Motilal Nehru National Institute of Technology, Allahabad, India
2Department of Electronics and Communication Engineering, Motilal Nehru National Institute of Technology, Allahabad, India
Email:*richa_negi123@yahoo.co.in, {spurwar, hnkar1}@rediffmail.com
Received November 11, 2011; revised December 13, 2011; accepted December 21, 2011
Keywords: Asymptotic Stability; Delay-Dependent Stability; Linear Matrix Inequality; Discrete System; Anti-Windup
ABSTRACT
This paper focuses on the study and the characterization of stability regions of discrete time systems with a time varying state delay subjected to actuator saturation through anti-windup strategies. Delay-dependent stability conditions are stated in the local as well as global context. An optimization procedure to maximize the estimate of domain of attraction is given. The proposed technique is illustrated by means of numerical examples.
1. Introduction
Over the last few decades, the study of time delay systems has received considerable attention in the context of control systems [1-3]. The presence of time delays leads to performance degradation and instability in many kinds of control systems like chemical, mechanical and biological systems [4,5]. Many publications relating to the issue of stability for time delay systems have appeared [6-13].
The problem of actuator saturation with or without time delay in the system has also received a lot of attention [14-18] in the past few years. The actuator saturation problem can be tackled using the anti-windup technique which augments the already existing linear controller with extra dynamics to minimize the adverse effect of saturation on the closed loop system. Several results are available where the anti-windup controller has been designed for continuous time delay systems subject to input saturation [19-24]. A state feedback controller design method for a class of continuous linear time delay systems with actuator saturation with time varying delays has been presented in [23]. The design of anti-windup compensator gain for stability of actuator input constrained state delay systems using constrained pole-position of the closed loop has been proposed in [24].
Several previous works [6-8,12,13] deal with the problem of global asymptotic stability of digital filters with state saturation. The nonlinearities considered in [6-8,12, 13] occur due to the implementation of the system using finite wordlength. In contrast, much less attention has been paid for the stability analysis of discrete time-delay systems subjected to input saturation.
The main objective of this paper is the study and characterization of regions of stability for discrete time delay systems subjected to input saturation through anti-windup strategies. The delay range dependent approach is adopted and the corresponding anti-windup compensator gain is obtained via LMIs formulation. Furthermore, the domain of attraction of the origin can be estimated for the underlying systems with different time delay ranges. The paper is organized as follow. Section 2 presents a description of the system under consideration. A delay-dependent linear matrix inequality (LMI) condition for the design of antiwindup compensator gain for stability of actuator input constrained state delay systems is proposed in Section 3. An optimization procedure to maximize the domain of attraction is also stated in this section. The effectiveness of the derived condition is presented through the numerical examples in Section 4.
Notations: 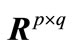 denotes the set of
denotes the set of 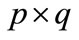 real matrices and the notation
real matrices and the notation 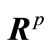 means the set of
means the set of  real matrices.
real matrices. 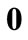 stands for the null matrix and
stands for the null matrix and  is an identity matrix of an appropriate dimension.
is an identity matrix of an appropriate dimension.  is the maximum eigenvalue of any given matrix
is the maximum eigenvalue of any given matrix  and transpose of this matrix is denoted by
and transpose of this matrix is denoted by . The symmetric entries in a symmetric matrix are given by
. The symmetric entries in a symmetric matrix are given by .
.
2. Problem Statement
Consider the discrete time linear system with a time varying delay
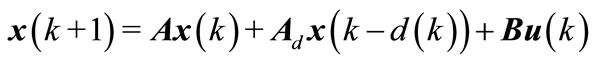 (1a)
(1a)
 (1b)
(1b)
where ,
,  ,
, 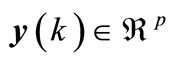 are the state, the input and measured output vectors respectively. Matrices
are the state, the input and measured output vectors respectively. Matrices ,
,  ,
, 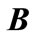 ,
, 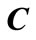 are constant matrices of appropriate dimensions, and
are constant matrices of appropriate dimensions, and 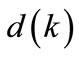 is a time varying delay satisfying
is a time varying delay satisfying
 (2)
(2)
For the system (1) the dynamic output stabilizing controller is considered as
 (3a)
(3a)
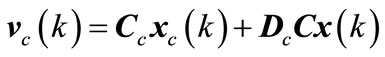 (3b)
(3b)
where  is the controller state and
is the controller state and  is the controller output. The controller (3) is to be designed to ensure the stability and the performance of the system in absence of the control saturation.
is the controller output. The controller (3) is to be designed to ensure the stability and the performance of the system in absence of the control saturation.
The input vector 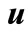 is subjected to the amplitude constraint as
is subjected to the amplitude constraint as
 (4)
(4)
where , denote the control amplitude bounds. Thus the actual control signal given into the plant is
, denote the control amplitude bounds. Thus the actual control signal given into the plant is
 . (5)
. (5)
The saturation nonlinearities are given by
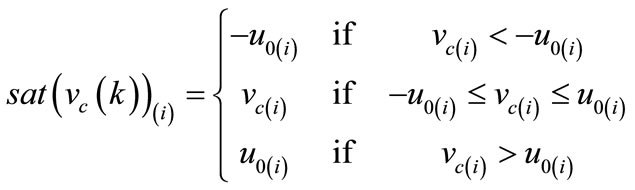 (6)
(6)
Substituting (5) in (1), one obtains
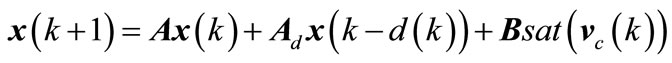 (7a)
(7a)
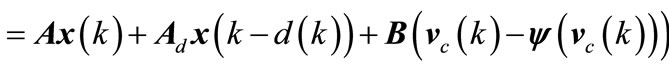 (7b)
(7b)
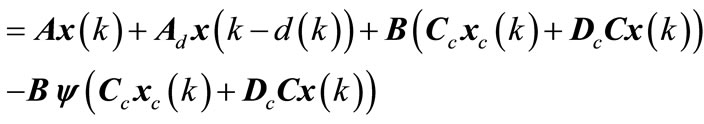 (7c)
(7c)
where
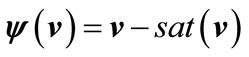 (8)
(8)
Adding an anti-windup term of the form 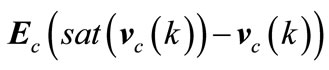 to the controller we get
to the controller we get
 (9)
(9)
Now define an extended state vector
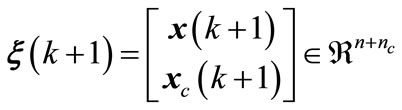 (10)
(10)
and the following matrices
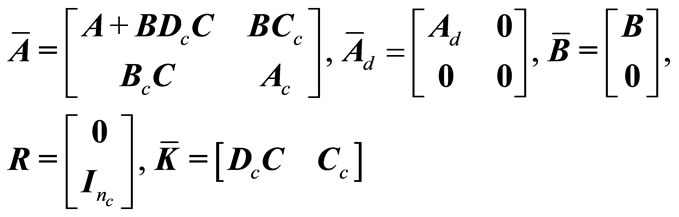 (11)
(11)
Using (1)-(11), the closed loop system can be expressed as
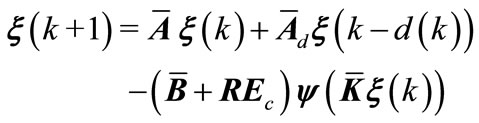 (12)
(12)
Let the solution of closed loop system given by (12) with the initial condition
 be
be 
Then the domain of attraction of the origin of system by (12) is
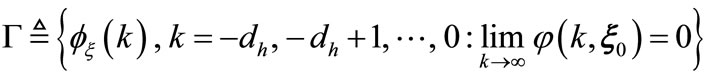 (13)
(13)
The main aim of this paper is to determine the antiwindup gain matrix  and a scalar
and a scalar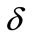 , as large as possible, such that the asymptotic stability of the closed loop system given by (12) is ensured for all time varying delays satisfying (2). Also, we are interested in obtaining an estimate of domain of attraction
, as large as possible, such that the asymptotic stability of the closed loop system given by (12) is ensured for all time varying delays satisfying (2). Also, we are interested in obtaining an estimate of domain of attraction 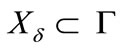 where
where
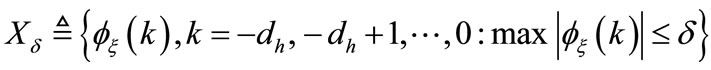 (14)
(14)
3. Delay-Dependent Stability Analysis
3.1. LMI-Based Stability Conditions
Consider a matrix  and define the polyhedral set
and define the polyhedral set
 (15)
(15)
In [25] it has been shown that
 (16)
(16)
where 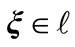 and
and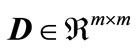 is a positive definite diagonal matrix.
is a positive definite diagonal matrix.
The main result may be stated as follows.
Theorem 1: For given positive integers 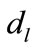 and
and 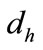 with
with , if there exist positive definite symmetric matrices
, if there exist positive definite symmetric matrices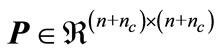 ,
,  ,
,
 ,
, 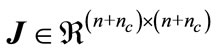 , and a diagonal positive definite matrix
, and a diagonal positive definite matrix ,
, 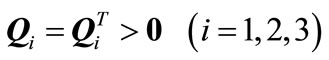 ,
, 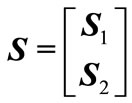
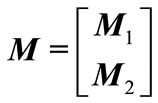
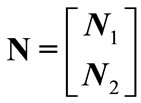
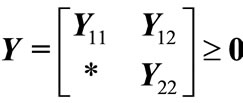
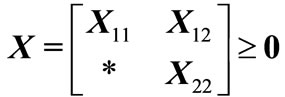
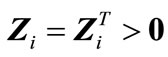
 ,
, , such that (17)-(21) hold,
, such that (17)-(21) hold,
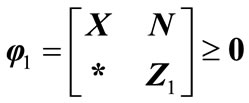 (18)
(18)
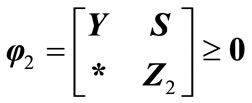 (19)
(19)
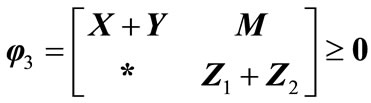 (20)
(20)
 (21)
(21)
where
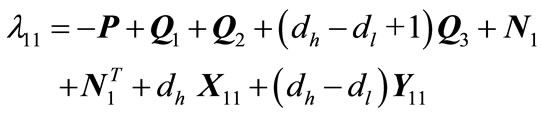 (22)
(22)
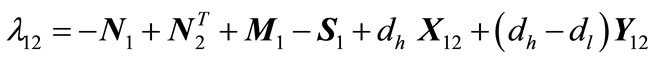 (23)
(23)
 (24)
(24)
then for the gain matrix , the closed loop system given by (12) is asymptotically stable and an estimate of the domain of attraction is given by
, the closed loop system given by (12) is asymptotically stable and an estimate of the domain of attraction is given by
 (25)
(25)
Proof: See the Appendix A.
Remark 1: To apply Theorem 1, initial guesses of the positive definite matrices  are tested until (17)-(21) have a feasible solution. Numerical experiences from the examples in the Section 4 suggest that useful initial choices can be
are tested until (17)-(21) have a feasible solution. Numerical experiences from the examples in the Section 4 suggest that useful initial choices can be  and
and
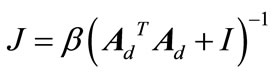 , where
, where 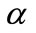 and
and 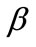 are positive constants [27].
are positive constants [27].
As a direct consequence of Theorem 1, we have the following result.
Corollary 1: For given positive integers 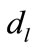 and
and 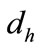 with
with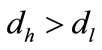 , if there exist positive definite symmetric matrices
, if there exist positive definite symmetric matrices ,
, 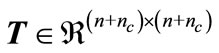 ,
, 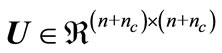 ,
, 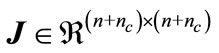 , a matrix
, a matrix  and a diagonal positive definite matrix
and a diagonal positive definite matrix , and the appropriately dimensioned matrices
, and the appropriately dimensioned matrices
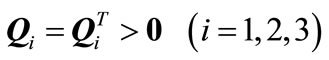 ,
, 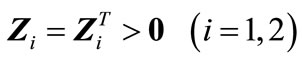 ,
,
 ,
, 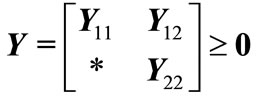 ,
, 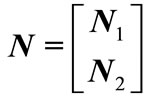 ,
,  ,
, 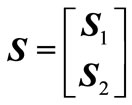 , such that
, such that
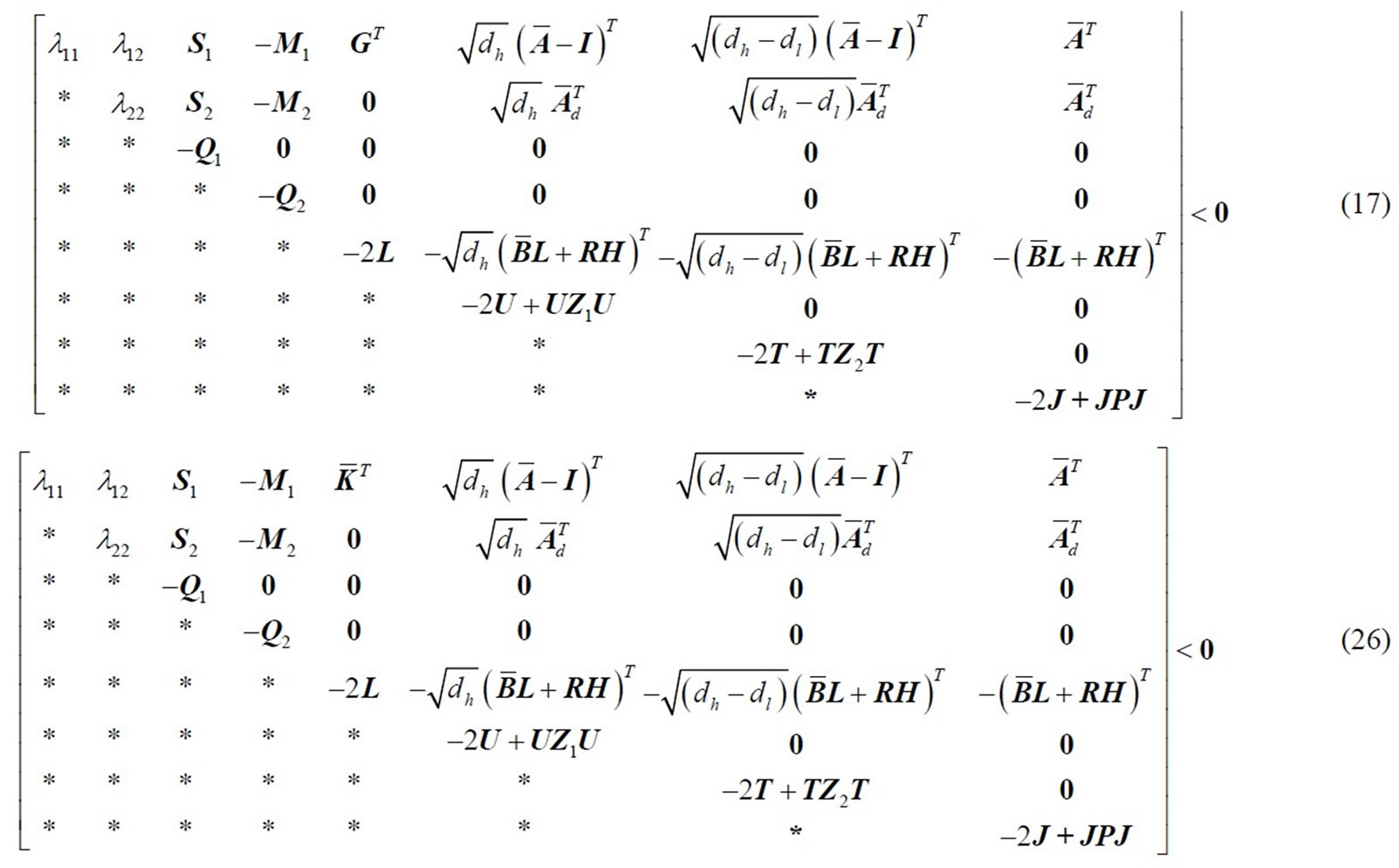
and (18)-(20) hold, for the gain matrix , the closed loop system given by (12) is globally asymptotically stable.
, the closed loop system given by (12) is globally asymptotically stable.
Proof: Consider . It follows that (15) is verified for all
. It follows that (15) is verified for all , then (17) corresponds to (26).
, then (17) corresponds to (26).
3.2. Maximization of the Estimate of Domain of Attraction
The following theorem gives an optimization procedure to maximize the estimate of domain of attraction.
Theorem 2: Consider the closed loop system (12) with the initial conditions (13) then the maximized domain of attraction can be estimated if the following convex optimization problem minimize r where
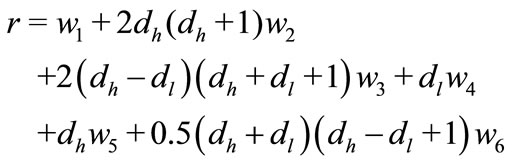 (27)
(27)
subject to (17)-(21) and
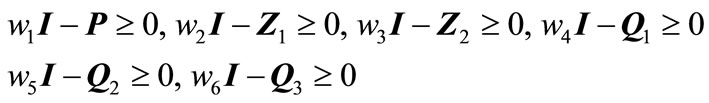 (28)
(28)
has a feasible solution for the weighting parameters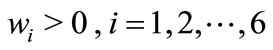 , positive definite symmetric matrices
, positive definite symmetric matrices ,
,  ,
,  ,
,  , and a diagonal positive definite matrix
, and a diagonal positive definite matrix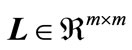 ,
,  ,
,
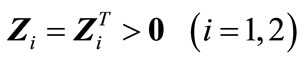

In this situation, an anti-windup gain  provides a maximized estimate of domain of attraction given by
provides a maximized estimate of domain of attraction given by 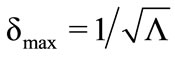 , where
, where
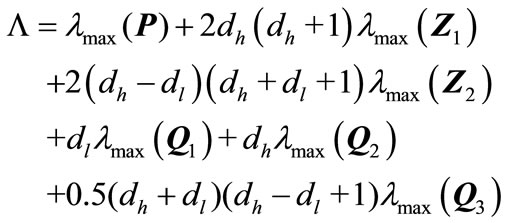 (29)
(29)
Proof: The satisfaction of relation (28) implies that
 ,
,  ,
, 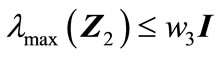 ,
,
 ,
,  ,
, .
.
From (25), one has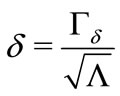 . Thus, if we minimize (27),
. Thus, if we minimize (27), 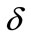 is being maximized. In other words, the optimization problem given in Theorem 2 orients the solutions of (17)-(21) in order to obtain the domain of attraction as large as possible.
is being maximized. In other words, the optimization problem given in Theorem 2 orients the solutions of (17)-(21) in order to obtain the domain of attraction as large as possible.
4. Examples
To illustrate the applicability of the presented results, we now consider the following examples. The first one is provided to check the validity of the results in the local stability context, while the second one demonstrates the global asymptotical stability.
Example 1. Consider the discrete time state delayed system (1) and stabilizing controller (3) with

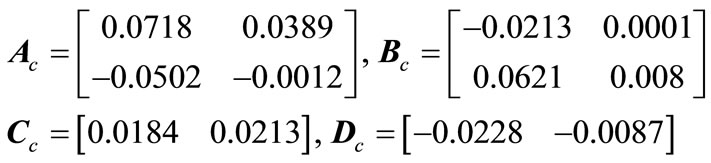
The control signal injected into the plant is a saturated one characterized by (6) where

Applying Theorem 2 and using Matlab (version 7.4) LMI toolbox [28,29] the anti-windup controller gains and the estimated domain of attraction for different delay ranges for the present system are obtained as shown in Table 1.
The state trajectories of the closed loop system for 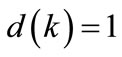 are depicted in Figures 1 and 2. As shown in Figure 1, the states of plant given by
are depicted in Figures 1 and 2. As shown in Figure 1, the states of plant given by 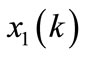 and
and 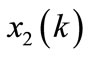 converge to zero. The controller states represented by
converge to zero. The controller states represented by  and
and  also converge to zero (see Figure 2). Figure 3 shows the plot of the unconstrained controller output
also converge to zero (see Figure 2). Figure 3 shows the plot of the unconstrained controller output 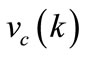 and the plant input
and the plant input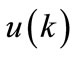 .
.
Example 2. Consider the discrete time state delayed system (1) and stabilizing controller (3) with

Table 1. Computation results of Example 1.

Figure 1. Trajectory of plant states.
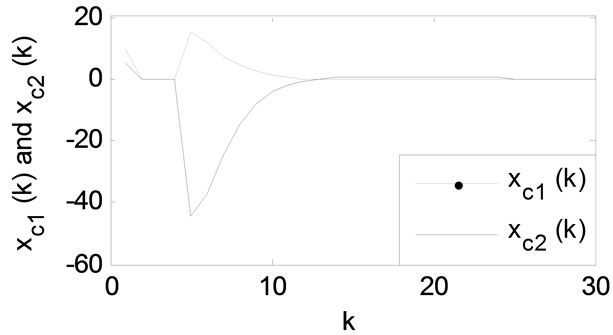
Figure 2. Trajectory of controller states.

Figure 3. Plot of vc(k) and u(k).

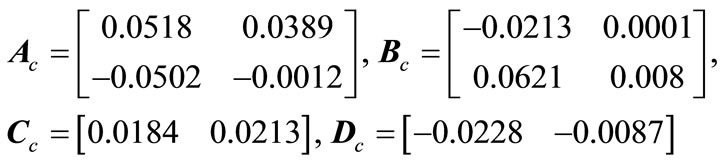
It is found that the conditions stated in Corollary 1 are feasible for the present example. Therefore, Corollary 1 assures the global asymptotic stability of the system under consideration and the anti-windup controller gain is obtained as

5. Conclusions
The control problem for linear discrete time delay systems subjected to input saturation through anti-windup strategies is investigated in this paper. The time delay is considered to be time varying. A delay range dependent approach is used and the corresponding LMI based stabilizing anti-windup compensator gain is obtained. An estimate of domain of attraction of the origin is also derived for the given system with different time delay ranges.
Recently, the delay-partitioning approach for the stability analysis of linear discrete time systems with time varying delay has been reported in [30]. As demonstrated in [30], the idea of delay-partitioning may lead to less conservative stability results. By utilizing the idea of delay-partitioning [30], the stability analysis of time delayed discrete systems subjected to input saturation appears to be an interesting problem and open for future investigation.
REFERENCES
- J. Richard, “Time-Delay System: An Overview of Some Recent Advances and Open Problems,” Automatica, Vol. 39, No. 10, 2003, pp. 1667-1697. doi:10.1016/S0005-1098(03)00167-5
- U. Shaked, I. Yaesh and C. E. DeSouza, “Bounded Real Criteria for Linear Time Delay Systems,” IEEE Transactions on Automatic Control, Vol. 43, No. 7, 1998, pp. 1016-1022. doi:10.1109/9.701117
- H. H. Choi and M. J. Chung, “An LMI Approach to H∞ Controller Design for Linear Time Delay Systems,” Automatica, Vol. 33, No. 4, 1997, pp. 737-739. doi:10.1016/S0005-1098(96)00242-7
- E. Fridman, A. Pila and U. Shaked, “Regional Stabilization and H∞ Control of Time-Delay Systems with Saturating Actuators,” International Journal of Robust and & Nonlinear Control, Vol. 13, No. 29, 2003, pp. 885-907. doi:10.1002/rnc.852
- B. Lehman and K. Shujaee, “Delay Independent Stability Conditions and Decay Estimates for Time Varying Functional Differential Equations,” IEEE Transactions on Automatic Control, Vol. 39, No. 8, 1994, pp. 1673-1676. doi:10.1109/9.310048
- M. S. Mahmooud, “Robust Control and Filtering for Timedelay System,” Maecel-Dekker, New York, 2000.
- S. F. Chen, “Asymptotic Stability of Discrete-Time System with Time-Varying Delay Subject to Saturation Nonlinearities,” Chaos, Solitons and Fractals, Vol. 42, No. 2, 2009, pp. 1251-1257. doi:10.1016/j.chaos.2009.03.026
- S.-I. Niculescu, “Delay Effects on Stability. A Robust Control Approach,” Springer-Verlag, Berlin, 2000.
- V. L. Kharitonov and S.-I. Niculescu, “On the Stability of Linear Systems with Uncertain Delay,” IEEE Transactions on Automatic Control, Vol. 48, No. 1, 2003, pp. 127- 132. doi:10.1109/TAC.2002.806665
- K. Gu and S.-I. Niculescu, “Survey on Recent Results in the Stability and Control of Time Delay Systems,” Journal of Dynamic Systems, Measurement and Control, Vol. 125, No. 2, 2003, p. 158.
- V. K. R. Kandanvli and H. Kar, “An LMI Condition for Robust Stability of Discrete-Time State-Delayed System Using Quantization/Overflow Nonlinearities,” Signal Processing, Vol. 89, No. 11, 2009, pp. 2092-2102. doi:10.1016/j.sigpro.2009.04.024
- V. K. R. Kandanvli and H. Kar, “Robust Stability of Discrete-Time State-Delayed Systems with Saturation Nonlinearities; Linear Matrix Inequality Approach,” Signal Processing, Vol. 89, No. 2, 2009, pp. 161-173. doi:10.1016/j.sigpro.2008.07.020
- V. K. R. Kandanvli and H. Kar, “Delay-Dependent LMI Condition for Global Asymptotic Stability of Discrete Time Uncertain State Delayed Systems Using Quantization/Overflow Nonlinearities,” International Journal of Robust Nonlinear Control, Vol. 21, No. 14, 2011, pp. 1611-1622. doi:10.1002/rnc.1654
- S. Oucherih, “Global Stabilization of a Class of Linear Continuous Time Delay System with Saturating Controls,” IEEE Transactions on Circuit and System I: Fundamental Theory and Applications, Vol. 43, No. 12, 1996, pp. 1012-1015.
- S. Tarbourieh and J. M. Gomes da Silva Jr., “Synthesis of Controllers for Continuous-Time Delay Systems with Saturating Control via LMI,” IEEE Transactions on Automatic Control, Vol. 45, No. 1, 2000, pp. 105-111. doi:10.1109/9.827364
- Y. Y. Cao, Z. L. Lin and T. Hu, “Stability Analysis of Linear Time-Delay Systems Subject to Input Saturation,” IEEE Transactions on Circuits and System (II), Vol. 49, No. 2, 2002, pp. 233-240. doi:10.1109/81.983870
- O. Said, “Synthesis of Controllers for Time-Delay Systems Subject to Actuator Saturation and Disturbance,” Journal of Dynamic Systems Measurement, and Control, Vol. 125, No. 2, 2003, pp. 244-249. doi:10.1115/1.1570450
- E. Tissir and A. Hmamed, “Further Results on The stabilization of Time Delay Systems Containing Saturating Actuators,” International Journal of Systems Science, Vol. 23, No. 4, 1992, pp. 615-622.
- J. M. Gomes da Silva Jr. and S. Tarbouriech, “Using Anti-Windup Loops for Enlarging the Stability Regions of Time-Delay Systems Subject to Input Saturation,” Proceedings of the 2004 American Control Conference, Boston, 30 June-2 July 2004, pp. 4819-4824.
- W. Y. Qiang, Y. Y. Cao and Y. X. Sun, “Anti-Windup Compensator Gain Design for Time Delay Systems with Constraints,” Acta Automatica Sinica, Vol. 32, No. 1, 2006, pp. 1-8.
- S. Tarbouriech, J. M. Gomes Da Silva Jr. and G. Garcia, “Delay-Dependent Anti-Windup Loops for Enlarging the Stability Region of Time Delay Systems with Saturating Inputs,” ASME Journal of Dynamic Systems, Measurment, and Control, Vol. 125, No. 2, 2003, pp. 265-267. doi:10.1115/1.1569953
- J. M. Gomes Da Silva Jr. and S. Tarbouriech, “AntiWindup Design with Guaranteed Regions of Stability: An LMI-Based Approach,” IEEE Transactions on Automatic Control, Vol. 50, No. 1, 2005, pp. 106-111. doi:10.1109/TAC.2004.841128
- L. Zhang, E. K. Boukas and A. Haidar, “Delay Range Dependent Control Synthesis for Time Delay Systems with Actuator Saturation,” Automatica, Vol. 44, No. 10, 2008, pp. 2691-2695. doi:10.1016/j.automatica.2008.03.009
- A. Ahmed, M. Rehan and N. Iqbal, “Delay-Dependent Anti-Windup Synthesis for Stability of Constrained State Delay Systems Using Pole-Constraints,” ISA Transactions, Vol. 50, No. 2, 2011, pp. 249-255. doi:10.1016/j.isatra.2010.11.003
- J. M. Gomes da Silva Jr. and S. Tarbouriech, “AntiWindup Design with Guaranteed Regions of Stability for Discrete Time Linear Systems,” System and Control Letters, Vol. 55, No. 3, 2006, pp. 184-192. doi:10.1016/j.sysconle.2005.07.001
- Y. He, M. Wu, G. P. Liu and J. H. She, “Output Feedback Stabilization for a Discrete-Time System with a TimeVarying Delay,” IEEE Transactions on Automatic Control, Vol. 53, No. 10, 2008, pp. 2372-2377. doi:10.1109/TAC.2008.2007522
- K. F. Chen and I. K. Fong, “Stability Analysis and Output-Feedback Stabilization of Discrete Time Systems with an Interval Time-Varying State Delay,” IET Control Theory and Application, Vol. 4, No. 4, 2010, pp. 563-572. doi:10.1049/iet-cta.2009.0100
- P. Gahinet, A. Nemirovski, A. J. Laub and M. Chilali, “LMI Control Toolbox—For Use with MATLAB,” MATH Works Inc., Natic, 1995.
- S. Boyd, L. EI-Ghaousi, E. Feron and V. Balakrishnan, “Linear Matrix Inequalities in Systems and Control Theory,” SIAM, Philadelphia, 1994. doi:10.1137/1.9781611970777
- X. Meng, J. Lam, B. Du and H. Gao, “A Delay Partitioning Approach to the Stability Analysis of Discrete Time Systems,” Automatica, Vol. 46, No. 3, 2010, pp. 610-614. doi:10.1016/j.automatica.2009.12.004
Appendix A
Proof of Theorem 1
Let
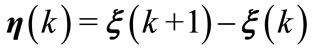 (A1)
(A1)

 (A2)
(A2)
Consider a quadratic Lyapunov function [26]
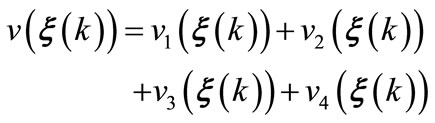 (A3)
(A3)
 (A4)
(A4)
 (A5)
(A5)
 (A6)
(A6)
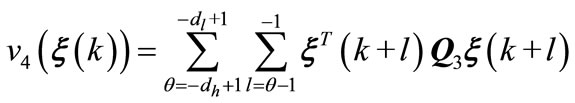 (A7)
(A7)
Defining
 (A8)
(A8)
gives
 (A9)
(A9)
 (A10)
(A10)
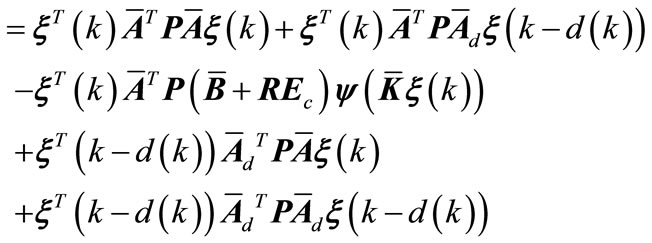

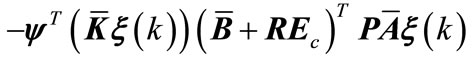

 (A11)
(A11)

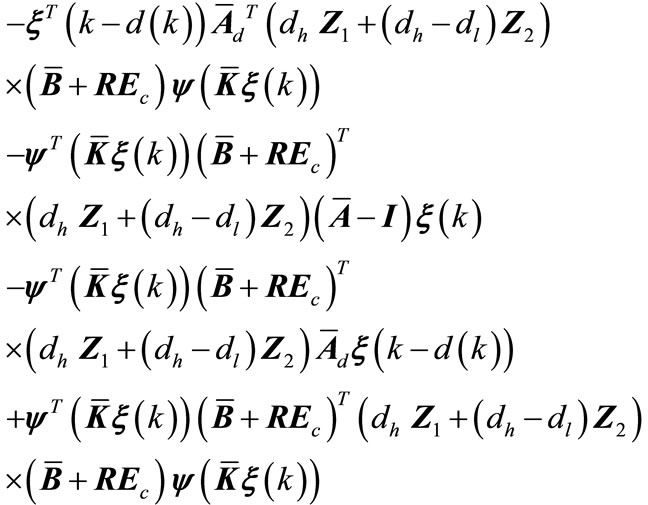

 (A12)
(A12)
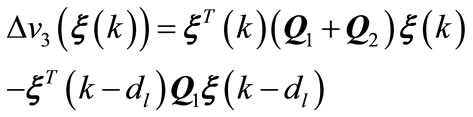
 (A13)
(A13)

 (A14)
(A14)
From (A1), we obtain
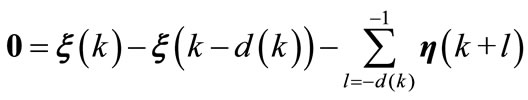 (A15)
(A15)
 (A16)
(A16)
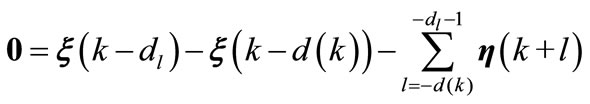 (A17)
(A17)
which, in turn, implies
 (A18)
(A18)
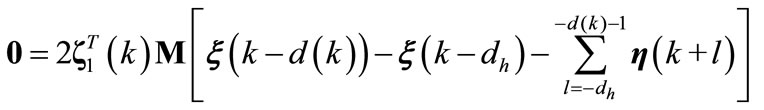 (A19)
(A19)
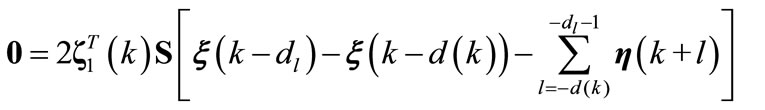 (A20)
(A20)
where
 (A21)
(A21)
Let 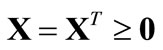 and
and  be any matrices of appropriate dimensions, then the following equations hold
be any matrices of appropriate dimensions, then the following equations hold

 (A22)
(A22)
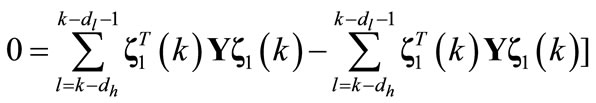
 (A23)
(A23)
Using (A9)-(A14) and (A18)-(A23), we have the following inequality
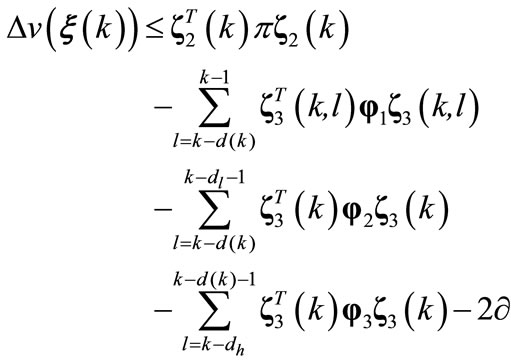 (A24a)
(A24a)
where  is given by (16) and
is given by (16) and
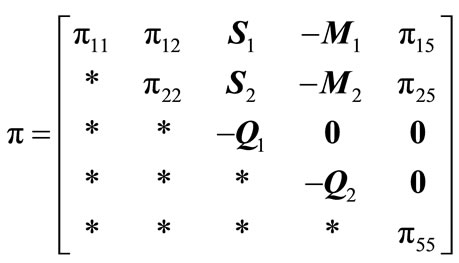 (A24b)
(A24b)
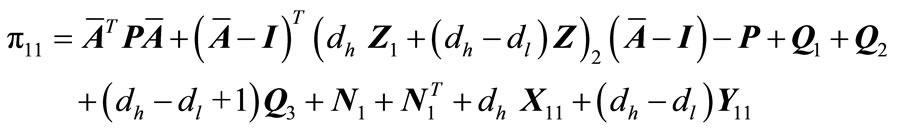 (A24c)
(A24c)
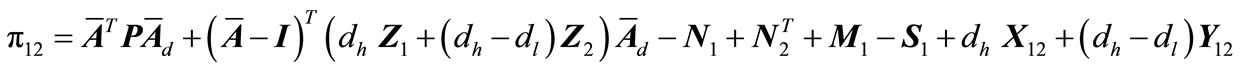 (A24d)
(A24d)
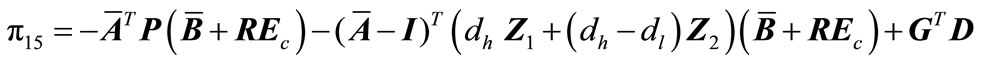 (A24e)
(A24e)
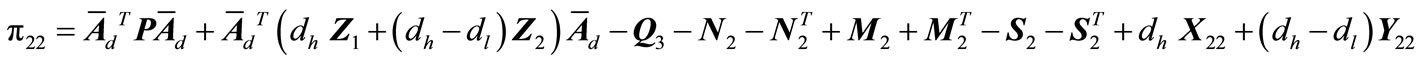 (A24f)
(A24f)
 (A24g)
(A24g)
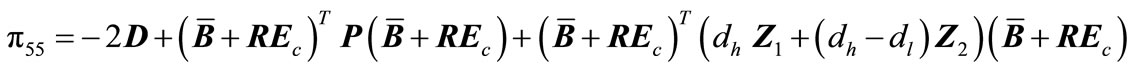 (A24h)
(A24h)
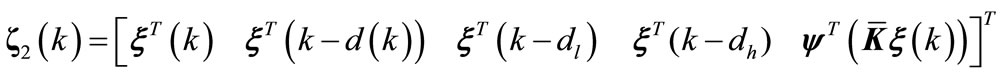 (A24i)
(A24i)
 (A24j)
(A24j)
In view of (18)-(20), it follows from (A24a) that
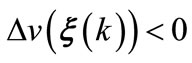 if
if
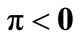 (A25)
(A25)
Using Schur complement [29], (A25) is equivalent to
 (A26a)
(A26a)
 (A26b)
(A26b)
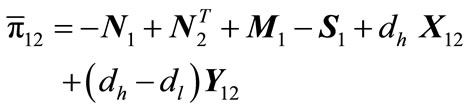 (A26c)
(A26c)
 (A26d)
(A26d)
Pre and post multiplying (A26a) by

yields
 (A27)
(A27)
where  and
and . For all
. For all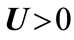 ,
,  and
and , we have
, we have
 (A28)
(A28)
 (A29)
(A29)
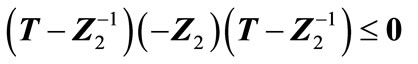 (A30)
(A30)
Therefore,
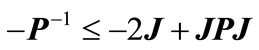 (A31)
(A31)
 (A32)
(A32)
 (A33)
(A33)
Using (A31)-(A33), it is easy to see that (A27) is implied by (17).
The satisfaction of relation (21) shows that the set 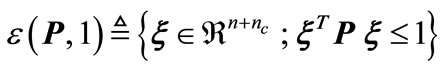 is included in the polyhedral set
is included in the polyhedral set 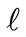 defined as in (15). Hence,
defined as in (15). Hence, 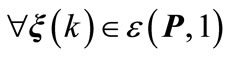 it follows that,
it follows that,
 satisfies the sector condition (16).
satisfies the sector condition (16).
Then, if (17) is verified one gets 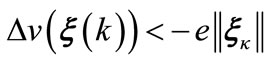
for a sufficiently small 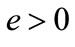 and accordingly,
and accordingly,
 (A34)
(A34)
Hence, if the set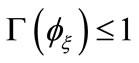 , then
, then  is also verified. Therefore, all the trajectories of
is also verified. Therefore, all the trajectories of  that start from
that start from 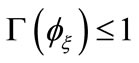 remain in domain of attraction provided (21) is satisfied ensuring the asymptotic stability of the closed loop system (12).
remain in domain of attraction provided (21) is satisfied ensuring the asymptotic stability of the closed loop system (12).
This completes the proof.
NOTES
*Corresponding author.

