Materials Sciences and Applications
Vol.06 No.02(2015), Article ID:53798,6 pages
10.4236/msa.2015.62018
A New Method to Determine the Maximum Value of the Track Length of Alpha Particle in CR-39 Detector
Hussein A. Ahmed, A. Mohammed, A. Said Ahmad
Department of Physics, Faculty of Science, University of Zakho, Duhok, Iraq
Email: pahmedhussein@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 January 2015; accepted 29 January 2015; published 4 February 2015
ABSTRACT
The aim of this paper is to determine the maximum values of the track length (Lmax) of alpha particles in Nuclear Track Detector (type CR-39) using a new method by taking the relation between the etching time and the diameter square of alpha particle with different energies at constant bulk etch rate VB (1.45 µm/hr) by using TRACK_TEST program from Brun et al. function and Yu et al. function. Using the new equation, the maximum values of the track lengths of alpha particles measured in CR-39 detector have been found to be in a good agreement with the values measured by using Brun et al. function and Yu et al. function in TRACK_TEST program.
Keywords:
Maximum Value of Track Length, CR-39, Range of Alpha Particle, Nuclear Track Detector (NTD)

1. Introduction
A heavy charged particle leads to intensive ionization when it passes through matter. Along the path of the particle, a zone called the latent track is created, which is enriched with free chemical radicals and other chemical species. If a piece of material containing the latent track is exposed to some chemically aggressive solution (such as aqueous NaOH or KOH solution), the chemical reaction would be more intensive in the latent track. Such a solution is called the etchant. Through the etching, the latent track becomes visible as a particle “track” which may be seen under an optical microscope. The effect itself has been known for a long time, which is called the “track effect” [1] . The technique has been extensively investigated in the literature, and has been widely applied in many fields of science and technology [2] . The main use of CR-39 plastic detector is in the field of health physics, such as detection of proton, helium and heavy charged particle, radon monitoring and neutron dosimetry [3] .
Characteristics of solid state nuclear track detectors were studied by many authors. It is well known that, track size, bulk etch rate and track etch rate are affected by exposing detectors to several types of radiations such as, X-ray, G-rays, UV and alpha particles. The two main changes noticed in polymers are:
1) chain cross-linking resulting in an increase of molecular weight because of a large number of free radicals produced in polymer;
2) chain scission resulting in a decrease of molecular weight and substantially changing in polymer material properties. In addition to these changes, small molecules such as Co, Co2 and H2 may be produced resulting from bond scission [4] .
There is no complete theory so far which completely describes the physics of track formation. In spite of the fact that such theory is not so essential as far as SSNTD practical uses are concerned, the problem is still an open one. Thus, the problem of the track development geometry has been the subject of many studies in recent years. Emphases have been paid on two aspects of three dimensional track developments upon etching. The first is an experimental one. This involves the use of atomic force microscopes [5] -[7] and confocal microscopy techniques [8] -[11] to obtain a direct view of the track profiles in three dimensions. The second type of studies is mainly concerned with geometrical equations related to track shapes upon different etching times [2] [12] -[14] . Both normal and oblique incidences have been treated. A user computer program that can calculate track profiles under different conditions has been presented by Nikezic and Yu [1] . A new empirical equation describing the development of charged particles radiation track against etching time and the longitudinal depth of track is presented [15] .
We can determine the maximum value of the track’s length corresponding to the energy of alpha particles, while the conical shape of the etch pit turns to a hemispherical shape. This occurs, when the total particle range is etched. Further prolongation of the etching time does not result in further growing of the track length, because the etching now takes place with the bulk etch rate in all directions [16] .
GyAlmasi et al. proposed an equation to find the range of alpha particles theoretically by using over-etched track profile technique [17] :
 (1)
(1)
We proposed a new equation to determine the maximum values of the track lengths (Lmax) of alpha particles in CR-39 detector depending on Equation (1), but after multiplying it with a specific parameter to get the value of the track length at energy of each alpha particle.
2. Experiment
We got the maximum values of the track lengths and the values of the diameters of alpha particles in CR-39 detector at different duration times of etching process from Nikezic and Yu et al. function and from Brun et al. function by using TRACK_TEST program for the same energies of alpha particles (2.5, 3.0, 3.6 and 4.0) MeV and with the same bulk etch rate (1.45 µm/hr) for the two functions.
3. Results and Discussion
The values of diameter square (D2) have been plotted versus etching time (t) for the data that we obtained from Brun et al. function [18] , and from Nikezic and Yu et al. function [19] by using TRACK_TEST program [1] for CR-39 detector for the two functions with different energies of alpha particles as shown in (Figures 1-4). We showed from the figures the non-linear relationships between the etching time and the diameter squares of the of alpha particles and by taking the fitting of the straight line of the curve we measured the slope of the linear part and the intercept with the x-axis, and then we could calculate the Lmax of alpha particle in the CR-39 detector by using the Equation (1) but after multiplying it with 2.56.
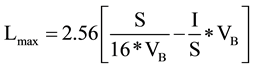 (2)
(2)
where S is the slope of straight line of D2 and t relation and I is the intercept of straight line with x-axis.
Figure 1. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 2.5 MeV by using Brun et al. function.
Figure 2. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 3.0 MeV by using Brun et al. function.
Figure 3. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 3.6 MeV by using Brun et al. function.
Figure 4. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 4.0 MeV by using Brun et al. function.
While VB is constant and equal to 1.45 µm/hr [20] , and it is determined from the change in the mass of the detector ∆m and the density of the detector material [21] [22] and it is based on Equation (3):
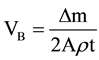 (3)
(3)
where Δm is mass difference, A is the etched surface area, ρ is the density of the detector and t is the etching time.
We found the parameter 2.56. By comparing the results of Lmax that we obtained directly from Brun et al. function by using TRACK_TEST program with the results that we obtained by using Equation (1), we observed that Equation (1) will give me correct results for the maximum values of the track length alpha particles if we multiplied it with 2.56. and we found this parameter by dividing the value of Lmax from Brun et al. function over the theoretical value of Lmax from Equation (1) for the same used energy, and after multiplying the theoretical values that we obtained by using Equation (1) by the factor 2.56 (Equation (2)), we got values very close to the maximum values of the track lengths that we obtained directly from Brun et al. function [18] by using TRACK_TEST program [1] .
Let us now take the same kind of Lmax measurements directly from Yu et al. function [19] in TRACK_TEST program [1] , and then compare the results of Lmax theoretically that we obtained by using Equation (2) from the data between the etching time and the diameter square (t & D2) that we obtained from Yu et al. function [19] in TRACK_TEST program [1] . We found that Equation (2) gave good results of Lmax comparing it with the values of Lmax that have obtained directly by using Yu et al. function in TRACK_TEST program. Figures 5-7 and Figure 8 show the relation between etching time and the diameter square.
Table 1 shows the comparison between the values of Lmax for alpha particles in CR-39 at different energies from Brun et al. function [18] by using TRACK_TEST program [1] , and the theoretical method by using Equation (2). It is clear that there is a good agreement between the values of Lmax that have been calculated theoretically by using Equation (2) and the values of Lmax from Brun et al. function by using TRACK_TEST program.
Table 2 shows the comparison between the values of Lmax for alpha particles in CR-39 at different energies from Yu et al. function [19] by using TRACK_TEST program [1] , and the theoretical method by using Equation (2). It is clear that there is a good agreement between the values of Lmax that have been calculated theoretically by using Equation (2) and the values of Lmax from Yu et al. function by using TRACK_TEST program.
4. Conclusion
The maximum values of the track lengths in CR-39 detector for different energies of alpha particles (2.5, 3.0, 3.6 and 4.0 MeV) have been calculated from a simple relation between the etching time and the diameter square of alpha particles from track diameter measurements. From the obtained results we found that Equation (2) will
Figure 5. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 2.5 MeV by using Yu et al. function.
Figure 6. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 3.0 MeV by using Yu et al. function.
Figure 7. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 3.6 MeV by using Yu et al. function.
Figure 8. Diameter square (D2) as a function of etching time (t) for alpha energy Eα = 4.0 MeV by using Yu et al. function.
Table 1. Comparison between the maximum values of track lengths in CR-39 detector for different values of α-particle energy theoretically and from Brun et al. functions.
Table 2. Comparison between the maximum values of track length in CR-39 detector for different values of α-particle energy theoretically and from Yu et al. function.
give good results for the maximum values of the track lengths (Lmax) of alpha particle with any energy in CR-39 detector.
References
- Nikezic, D. and Yu, K.N. (2006) Computer Program TRACK_TEST for Calculating Parameters and Plotting Profiles for Etch Pits in Nuclear Track Materials. Computer Physics Communications, 174, 160-165. http://dx.doi.org/10.1016/j.cpc.2005.09.011
- Nikezic, D. and Yu, K.N. (2003) Calculations of Track Parameters and Plots of Track Openings and Wall Profiles in CR39 Detector. Radiation Measurements, 37, 595-601. http://dx.doi.org/10.1016/S1350-4487(03)00080-5
- Jain, R.K., Kumar, A., Chakraborty, R.N. and Nayak, B.K. (2013) The Response of CR-39 Plastic Track Detector to Fission Fragments at Different Environmental (Temperature) Conditions. Nuclear Physics, 58, 564-565.
- Abdel Raouf, Kh.M. (2013) Study of CR-39 SSNDs Irradiated with Different Types of Radiation by FTIR Spectroscopy and α-Range Determination. American Journal of Environmental Protection, 2, 53-57. http://dx.doi.org/10.11648/j.ajep.20130202.14
- Yu, K.N., Yip, C.W.Y., Ho, J.P.Y. and Nikezic, D. (2004) Application of Surface Profilometry in Studying the Bulk Etch of Solid State Nuclear Track Detectors. Current Issues on Multidisciplinary. Microscopy Research and Education, 253-256.
- Fragoso, R., Vazquez-Lopez, C., Golzarri, J.I. and Espinosa, G. (2007) Artifact Patterns in Atomic Force Microscopy on the Nuclear Track Studies. Acta Microscopica, 16, 157-158.
- Vazquez-Lopez, C., Fragoso, R., Golzarri, J.I. and Espinosa, G. (2007) Applications of the Atomic Force Microscopy to Nuclear Track Methodology. Revista Mexicana De Fisica, S53, 52-56.
- Fromm, M., Vaginay, F., Pusset, D., Meesen, G., Chambaudet, A. and Poffijn, A. (2001) 3-D Confocal Microscopy of Etched Nuclear Tracks in CR-39. Physica Medica, 17, 144-146.
- Fromm, M., Vaginay, F., Meesen, G., Chambaudet, A. and Poffijn, A. (2003) Watching at the Correlation between the Specific Track-Etch Rate and the Primary Physical Parameters of the Swift Ion Interaction with the CR-39. Radiation Measurements, 36, 93-98. http://dx.doi.org/10.1016/S1350-4487(03)00101-X
- Fromm, M., Awad, E.M. and Ditlov, V. (2004) Many-Hit Model Calculations for Track Etch Rate in CR-39 SSNTD Using Confocal Microscope Data. Nuclear Instruments and Methods in Physics Research Section B, 226, 565-574. http://dx.doi.org/10.1016/j.nimb.2004.07.004
- Vaginay, F., Fromm, M., Pusset, D., Meesen, G., Chambaudet, A. and Poffijn, A. (2001) 3-D Confocal Microscopy Track Analysis: A Promising Tool for Determining CR-39 Response Function. Radiation Measurements, 34, 123-127. http://dx.doi.org/10.1016/S1350-4487(01)00136-6
- Barillon, R., Fromm, M., Chambaudet, A., Marah, H. and Sabir, A. (1997) Track Etch Velocity Study in Radon Detector (LR 115, Cellulose Nitrate). Radiation Measurements, 28, 619-628.
- Nikezic, D., Yu, K.N. and Kostic, D. (2003) Three-Dimensional Model of Track Growth: Comparison with Other Models. Nuclear Technology and Radiation Protection, 2, 24-30. http://dx.doi.org/10.2298/NTRP0302024N
- Nikezic, D., Stevanovic, N., Kostic, D., Savovic, S., Tse, K.C.C. and Yu, K.N. (2008) Solving the Track Wall Equation by the Finite Difference Method. Radiation Measurements, 43, 576-578. http://dx.doi.org/10.1016/j.radmeas.2008.03.037
- Azooz, A.A., Al-Nia’emi, S.H. and Al-Jubbori, M.A. (2012) Empirical Parameterization of CR-39 Longitudinal Track Depth. Radiation Measurements, 47, 67-72. http://dx.doi.org/10.1016/j.radmeas.2011.10.015
- Dorschel, B., Hartmann, H. and Kadner, K. (1995) Variations of the Track Etch Rates along the Alpha Particle Trajectories in Two Types of CR-39. Radiation Measurements, 26, 51-57. http://dx.doi.org/10.1016/1350-4487(95)00270-7
- Almasi, G. and Somogyi, G. (1981) Range and REL Data for Light and Heavy Ions in CR-39, CN-85 and PC Nuclear Track Detectors. Atomki Kozlemenyek, 23, 99-112.
- Brun, C., Fromm, M., Jouffroy, M., Meyer, P., Groetz, J.E., Abel, F., Chambaudet, A., Dorschel, B., Hermsdorf, D., Bretschneider, R., Kadner, K. and Kunhe, H, (1999) Intercomparative Study of the Detection Characteristics of the CR-39 SSNTD for Light Ions: Present Status of the Besancon-Dresden Approaches. Radiation Measurement, 31, 89- 98. http://dx.doi.org/10.1016/S1350-4487(99)00102-X
- Yu, K.N., Ng, F.M.F. and Nikeic, D. (2005) Measuring Depths of Sub-Micron Tracks in a CR-39 Detector from Replicas Using Atomic Force Microscopy. Radiation Measurements, 40, 380-383. http://dx.doi.org/10.1016/j.radmeas.2005.03.011
- Ahmed, H.A. (2010) Tracks Profiles and Fitting It with the Theoretical Models for the Detector CR-39. M.Sc. Thesis, Physics Department, College of Education, University of Mosul, Mosul.
- Durrani, S.A. and Bull, R.K. (1987) Solid State Nuclear Track Detection. Pergamon Press, Oxford.
- Nikezic, D. and Yu, K.N. (2004) Formation and Growth of Tracks in Nuclear Track Materials. Materials Science and Engineers, 46, 51-123.










