Materials Sciences and Applications
Vol.3 No.9(2012), Article ID:22884,7 pages DOI:10.4236/msa.2012.39088
Ab Initio Study of Structural and Electronic Properties of Barium Chalcogenide Alloys
![]()
1Department of Physics, Faculty of Sciences, University Djillali Liabes, Sidi-Bel-Abbés, Algeria; 2Laboratory of Communication Networks, Architecture and Multimedia, Sidi-Bel-Abbès University, Sidi-Bel-Abbès, Algeria.
Email: *lttnsameri@yahoo.fr
Received May 12th, 2012; revised July 7th, 2012; accepted August 9th, 2012
Keywords: Semiconductor; FP-LMTO; Effective Mass
ABSTRACT
First-principles calculations have been used to study the structural and electronic properties of BaS1–xSex ternary alloy using full-potential muffin-tin orbital’s (FP-LMTO) method within density functional theory (DFT). In this approach, the local-density approximation (LDA) and generalized gradient approximation (GGA) are used for the exchange-correlation (XC) potential. The effect of composition on lattice parameter, bulk modulus, band gap and effective mass was investigated. The deviations of the lattice constant from Vegard’s law and the bulk modulus from linear concentration dependence were observed for BaS1–xSex alloy. The microscopic origins of bowing parameter were explained using approach of Zunger and co-workers. Accordance is found from the comparison of our results with other experimental and theoretical calculations.
1. Introduction
II-VI compounds have attracted great interest due to their potential applications in fields of light-emitting diodes (LEDs) and laser diodes (LDs) [1]. As important members of II-VI compounds, the Barium mono-chalcogenides; BaS and BaSe have already been systematically studied by both experiments and first-principles calculations [2,3] for many years, due to their interesting phase transition from the rocksalt crystal structure to the CsCl-crystal structure under pressure. The experimental [4,5] and theoretical [6] studies of BaX (X = S, Se) compounds have been made by many researchers. Most of available experimental results on the reflectivity and absorption of these compounds are limited to excitonic transitions [5-7]. From a theoretical point of view, the electronic properties of BaS, BaSe have been determined by Pourghazi and Dadsetani [8].
Recent works show that BaS1–xSex compounds have directed energy gaps, comparing with the indirect ones of BaS, BaSe. In this work, we report the structural and electronic calculations for BaS1–xSex (x = 0, 0.25, 0.50, 0.75 and 1) alloys using full potential muffin-tin orbital’s (FP-LMTO) method. The physical origins of gap bowing are calculated following the approach of Zunger and workers [9], in this approach, the alloy was studied in an ordered structure (we used here a cubic super cell of eight atoms) designed to reproduce the most important paircorrelation functions of random (disorder) alloy. In our calculations, we describe the method of calculation, results and discussion concerning structural, electronic, bowing parameters, effective masses and finally the conclusions.
2. Computational Methods
The calculations here were carried out using ab initio fullpotential linear muffin-tin orbital (FP-LMTO) method [10, 11] as implemented in the Lmtart code [12]. The exchange and correlation potential was calculated using the local density approximation (LDA) [13] and the generalized approximation (GGA) [14]. This is an improved method compared to previous LMTO methods. The FP-LMTO method treats muffin-tin spheres (MTS) and interstitial regions (IR) on the same footing, leading to improvements in the precision of the Eingenvalues.
At the same time, the FP-LMTO method, in which the space is divided into (IR) and non-overlapping (MTS) surrounding the atomic sites, uses a more complete basis than its predecessors. In the IR regions, the basis functions are represented by Fourier series. Inside the MTS, the basis functions are represented in terms of numerical solutions of the radial Schrödinger equation for the spherical part of the potential multiplied by spherical harmonics. The charge density and the potential are represented inside the MTS by spherical harmonics up to lmax = 6. The integrals over the Brillouin zone are performed up to 64 special k-points for binary compounds and 47 special k-points for the alloys in the irreducible Brillouin zone (IBZ), using the Blöchl’s modified tetrahedron method [15]. The self-consistent calculations are considered to be converged when the total energy of the system is stabled within 10–5 Ry. In order to avoid the overlap of atomic spheres the MTS radius for each atomic position is taken to be different for each case. Both the plane waves’ cut-off is varied to ensure the total energy convergence. The values of the sphere radii MTS, number of plane waves (NPLW), used in our calculation are summarized in Table 1.
3. Results and Discussion
3.1. Structural Properties
We have computed the structural properties of the binary compounds BaS and BaSe in the rocksalt structure. As for the semiconductor ternary alloy in the type BxA1–xC, we have started our FP-LMTO calculation of the structural properties with the rocksalt structure and let the calculation forces to move the atoms to their equilibrium positions. The BxA1–xC alloy are modelled some selected composition with ordered structures described in terms of periodically repeated supercels with eight atoms per unit cell of the compositions x = 0.25, 0.5 and 0.75. For the considered structures, we performed the structural optimization by calculating the total energies for different volumes around the equilibrium cell volume (V0) for BaS and BaSe binary compounds and their alloys. The calculated total energy at many different volumes around equilibrium were fitted to the Murnaghan’s equation of state [16] in order to obtain the equilibrium lattice constant and bulk modulus for the binary compounds and their alloys. The results of our calculations were summarized in Table 2, were com-

Table 1. The plane wave number PW, energy cut-off (in Ry) and muffin-tin radius (RMT) (in a.u.) used in calculation for binary BaS, BaSe and their alloys in rocksalt (NaCl) structure.
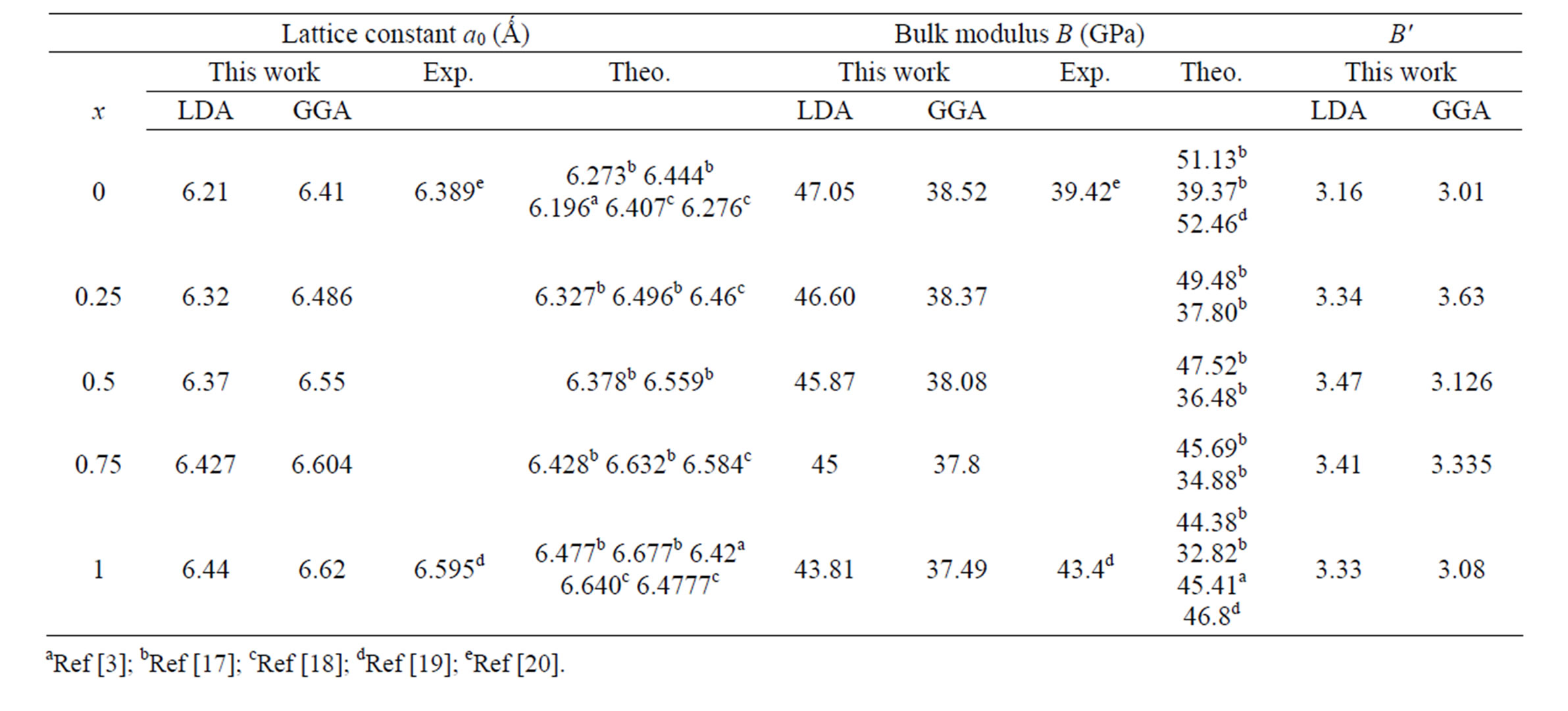
Table 2. Calculated lattice parameter (a0), bulk modulus (B) and its pressure derivative (B') compared to experimental and theoretical values of BaS and BaSe and their alloys.
pared to other experimental and theoretical calculations. It is observed that our calculated lattice parameters are in agreement with experimental data and theoretical work. Table 2 also indicates that GGA slightly overestimates while LDA underestimates the theoretical lattice parameter compared to the experimental results. As it can be seen that the calculated lattice parameter for BaS (x = 0) is smaller than those of BaSe (x = 1); a0 (BaS) < a0 (BaSe). The calculated Bulk modules, B as given in Table 2, agree with other experimental and theoretical calculations. It is observed that LDA gives bulk modulus closer to experiment while GGA approximation consistently tends to underestimate experiment. Furthermore, the values of the calculated bulk modulus using both approximations decreases from BaS to BaSe, suggesting that the compressibility increases from BaS to BaSe. The obtained pressure derivatives of bulk modulus are given in Table 2.
Usually, in the treatment of alloys, it is assumed that the atoms are located at the ideal lattice sites and the lattice constant varies linearly with the composition x according to the so-called Vegard’s law [21]:
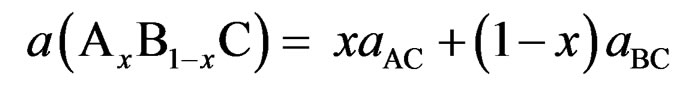 (1)
(1)
where aAC and aBC are the equilibrium lattice constants of the binary compounds AC and BC, respectively, and 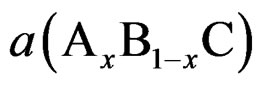 is the alloy lattice constant. However, deviation from Vegard’s law has been observed in semiconductor alloys both experimentally [22] and theoretically [23]. Hence, the lattice constant can be written as
is the alloy lattice constant. However, deviation from Vegard’s law has been observed in semiconductor alloys both experimentally [22] and theoretically [23]. Hence, the lattice constant can be written as
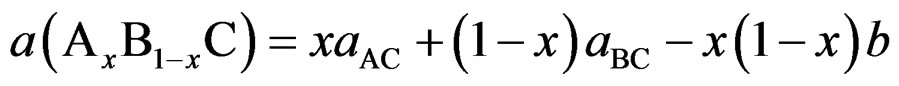 (2)
(2)
where the quadratic term (b) is the bowing parameter.
Figures 1 and 2 show the variation of the calculated equilibrium lattice constants and bulk modulus versus concentration x for BaS1–xSex alloy, The obtained results for the composition dependence of the calculated equilibrium lattice parameter show an excellent agreement to Vegard’s law [21]. In going from BaS to BaSe; when the Se-content increases, the values of the lattice parameters of the BaS1–xSex alloy increases. Oppositely, one can see from Figure 2 that the values of the bulk modulus decrease with increasing “Se” concentration. The values of the bowing parameters are determined by a polynomial fit. Using the LDA approximation, we obtained upward bowing parameters equal to –0.22 Å and –1.84 GPa for the lattice constant and bulk modulus, respectively. While, the GGA approximation gave values of –0.15 Å and –0.35 GPa for the bowing lattice parameter and the bulk modulus, respectively. The physical origin of this large deviation should be mainly due to the large mismatches of the lattice constants of BaS and BaSe compounds. But our results are relatively close to those of Ref. [17] obtained using the full potential-linear augmented plane wave (FP-LAPW) method.
3.2. Electronic Properties
The calculated band gap of binary compounds as well as their alloy using FP-LMTO method within LDA and GGA approximations gave a direct band gap at point Γ for BaS1–xSex with x varying between 0.25 and 0.75. For BaS and BaSe, the valence-band maximum (VBM) and the
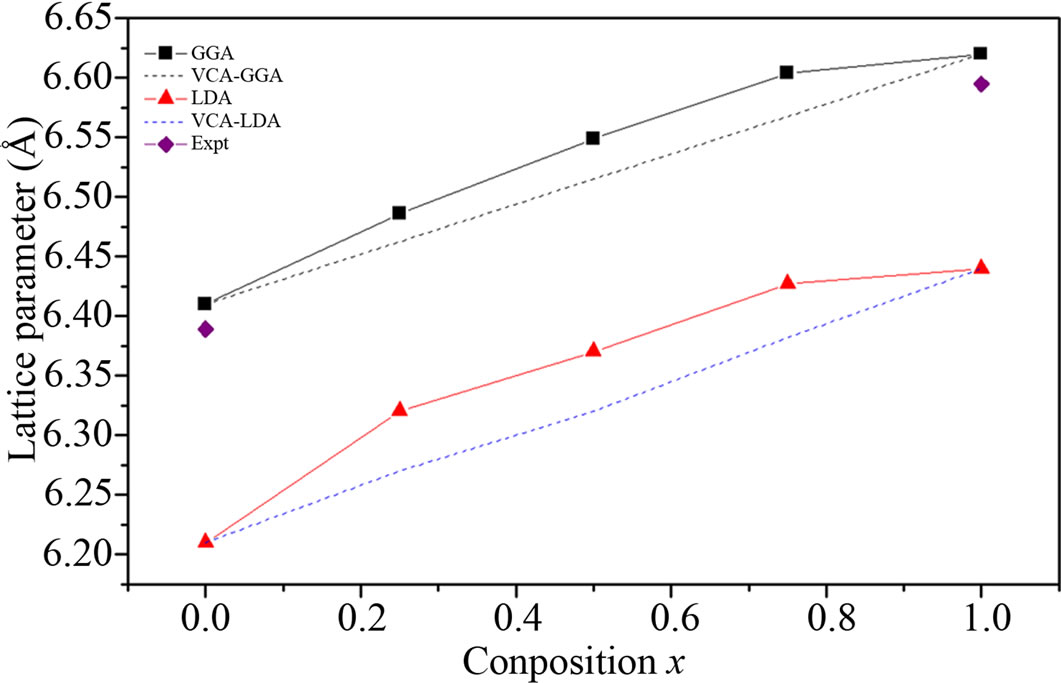
Figure 1. Composition dependence of the calculated lattice constants within LDA (solid circle) and GGA (solid triangle) of BaS1–xSex alloy compared with experimental (dotted line).

Figure 2. Composition dependence of the calculated bulk modulus within GGA (solid circle) and LDA (solid square) of BaS1–xSex alloy compared with experimental (dotted line).
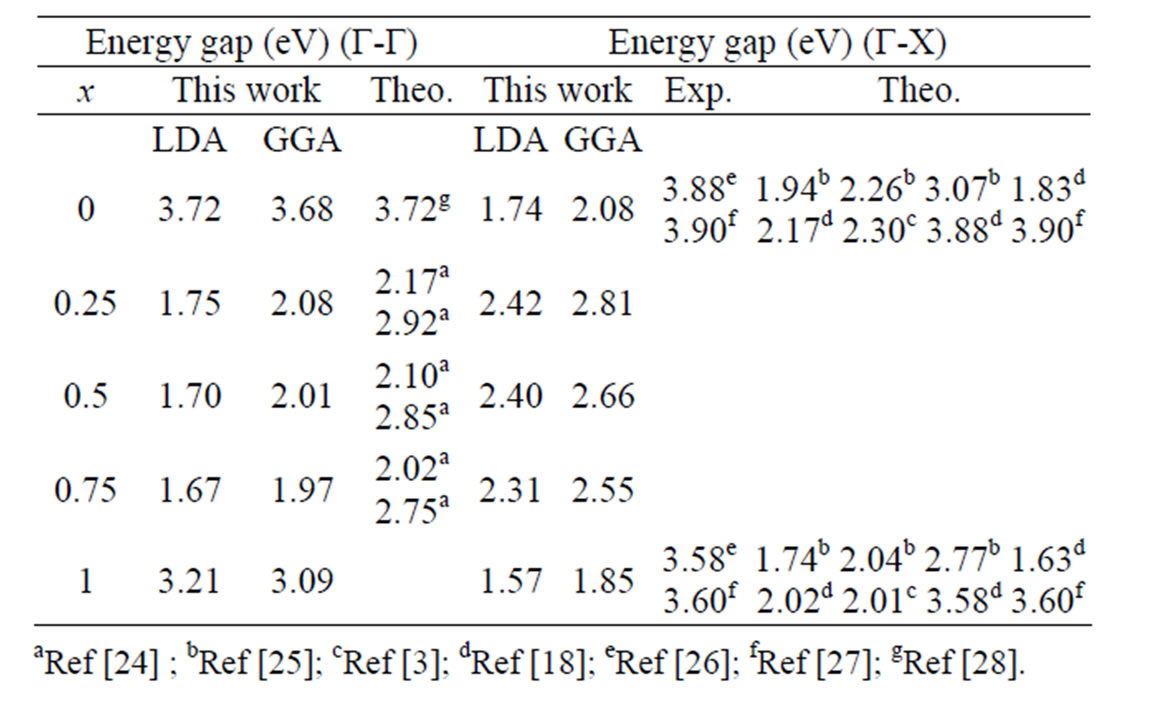
Table 3. Direct (Γ-Γ) and indirect (Γ-X) band gaps of BaS and BaSe and their alloy at different Se concentrations (all values are in eV).
conduction-band minimum (CBM) occurs at the Γ-and X-point, respectively. The principal energy gaps are given in Table 3, as well as the theoretical and the experimental ones.
It is well know that the LDA and the GGA usually underestimate the energy gap [29,30]. This is mainly due to the fact that they have simple forms that are not sufficiently flexible for accurately reproducing both exchange-correlation energy and its charge derivative. It is important to note that the density-functional formalism is limited in its validity [31] and the band structure derived from it cannot be used directly for comparison with the GW method, which is known to give energy band gaps in excellent agreement with experiment.
The important applications of BaS1–xSex alloy in optical devices require the determination of the band gap nature (direct or indirect band gap). The results of direct and indirect band gaps are given in Table 3. It is clear that the band gap values given by the LDA and GGA, are in a good agreement with the other computational works, but lower than the experimental work.
The variation of the direct EΓ-Γ and indirect EΓ-Γ band gaps of the alloys is shown in Figure 3. The calculated band structure yields an indirect gap (Γ-X) for BaS and BaSe, while for Se0.25S0.75Ba, Se0.5S0.5Ba and Se0.75S0.25Ba, a direct gap (Γ-Γ) has been determined. We calculated the total bowing parameter, by fitting the nonlinear variation,
We calculated the total bowing parameter, by fitting the nonlinear variation,
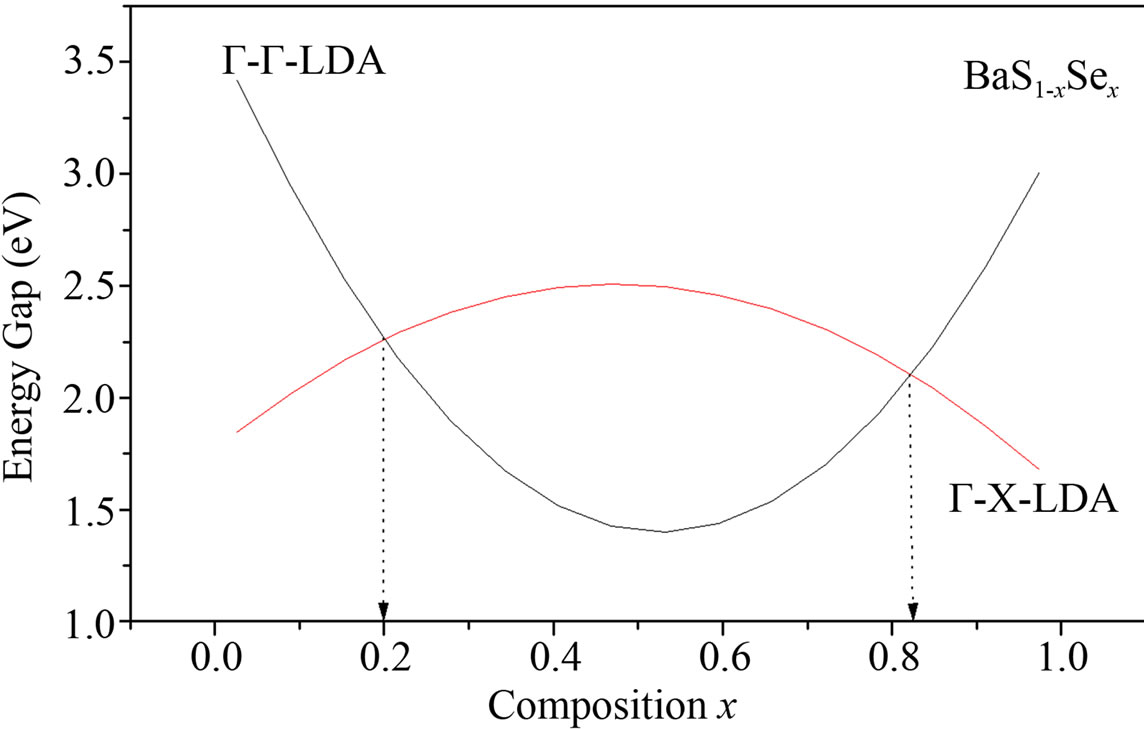
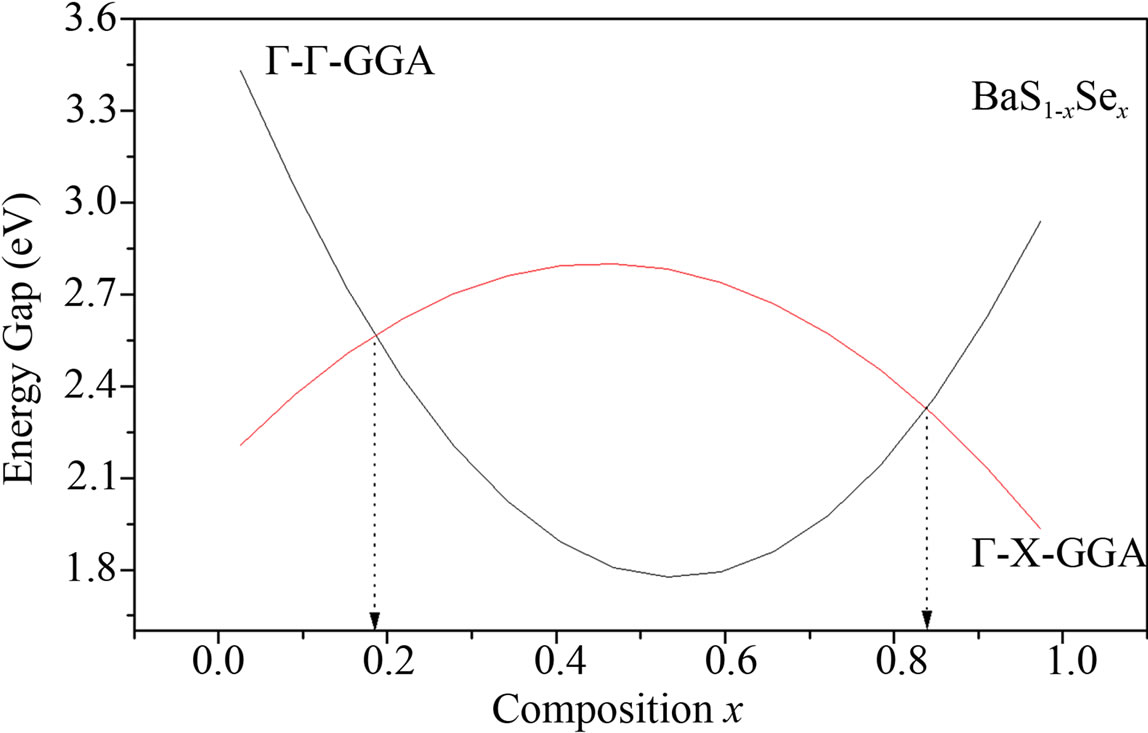
Figure 3. Energy band gap of BaS1–xSex alloy as a function of Se composition using LDA and GGA approximations.
with polynomial functions, of the calculated direct and indirect band gaps versus concentration. Using the LDA approximation, we could distinguish three regions: one direct band gap (Ґ-Ґ) for (0.19 ≤ x ≤ 0.82) and two other indirect band gaps (Ґ-X) for (0 ≤ x ≤ 0.19 and 0.82 ≤ x ≤ 1). The GGA approximation gave one direct band gap (Ґ-Ґ) for (0.18 ≤ x ≤ 0.84) and two other indirect band gaps (Ґ-X) for (0 ≤ x ≤ 0.18 and 0.84 ≤ x ≤ 1) It is clearly seen that our LDA values are in good agreement with the values found from the GGA.
And obey the following variations:
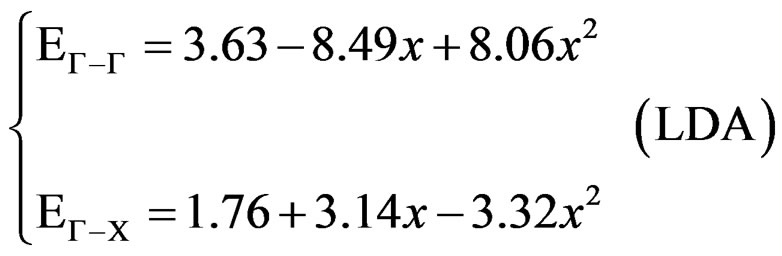 (3)
(3)
![]() BaS1–xSex
BaS1–xSex
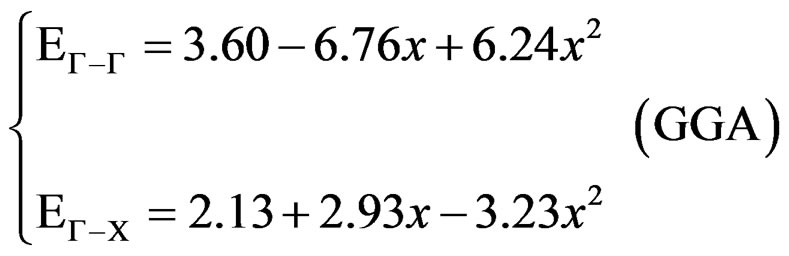 (4)
(4)
In order to attain a better understanding of the physical origin of the bowing parameters in BaS1–xSex alloy, we followed the procedure of Bernard and Zunger [9] and decomposed the total bowing parameter b into physically distinct contributions. The overall bowing coefficient at each composition x measures the change in the band gap according to the formal reaction
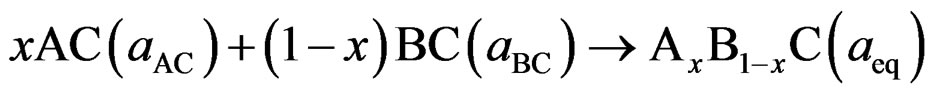 (5)
(5)
where BaSe and BaS are the equilibrium lattice constant of the binary compounds and aeq is the equilibrium lattice constant of the alloy with average composition x. Equation (5) is decomposed into three steps:
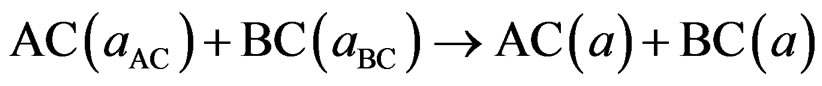 (6)
(6)
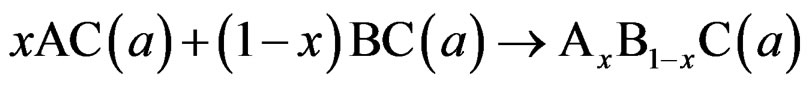 (7)
(7)
 (8)
(8)
The first step measures the volume deformation (VD) effect on the bowing. The corresponding contributions bVD to the bowing parameter represents the relative response of the band structure of the binary compounds BaSe and BaS to hydrostatic pressure, which here arises from the change of their individual equilibrium lattice constants to the alloy value a = a (x).
The second contribution, the charge exchange (CE) contribution bCE, reflects the charge transfer effect which is due to the different (averaged) bonding behaviour at the lattice constant a.
The last contribution, the so called “structural relaxation” (SR), measures changes in passing from the unrelaxed to the relaxed alloy by bSR. Consequently, the total bowing parameter is defined as
 (9)
(9)
The general representation of the composition dependent band gap of the alloy in terms of the binary compounds gaps is EBaSe (aBaSe), EBaS (aBaS), and the total bowing parameter b is given by
 (10)
(10)
This allows a splitting of the total bowing b into three contributions according to
 (11)
(11)
 (12)
(12)
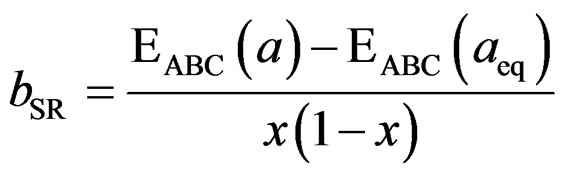 (13)
(13)
All of these energy gaps occurring in expressions (11)- (13) have been calculated for the indicated atomic structures and lattice constants.
The calculated bowing coefficients b calculated at molar fractions x = 0.25, 0.50 and 0.75 for BaS1–xSex alloy are listed in Table 4 using FP-LMTO method within LDA and GGA approximations. We note that the obtained bowing parameter for x = 0.5 is an excellent agreement with the others using EVGGA-FPLAPW method [24].
The small bCE value of BaS1–xSex alloy is due to the weak iconicity mismatch of BaS and BaSe. The importance of bVD can be correlated to the large mismatch of lattice constants of the corresponding binary compounds. Finally, it is clearly seen that our LDA values for total bowing parameters are better than the corresponding with in GGA in comparison with other. Figure 4 shows the variation

Table 4. Decomposition of optical bowing into volume deformation (VD), charge exchange (CE) and structural relaxation (SR) contributions (all values in eV).

Figure 4. Calculated band gap bowing parameter as a function of Se concentration within GGA (solid square) and LDA (solid circle).
of the band gap bowing versus concentration. The bowing remains linear and varies slowly for x = 0.5, and beyond x = 0.50 it decreases rapidly.
3.3. Calculated Effective Masses
Knowledge of the electron and hole effective mass values is indispensable for the understanding of transport phenomena, exciton effects and electro-hole in semiconductors. Excitonic properties are of great interest for binary BaS, BaSe and their alloys; therefore, it is worthwhile to estimate the electron and hole effective mass values for these materials. Experimentally, the effective masses are usually determined by cyclotron resonance, electro reflectance measurements, analysis of transport data or transport measurements [32].
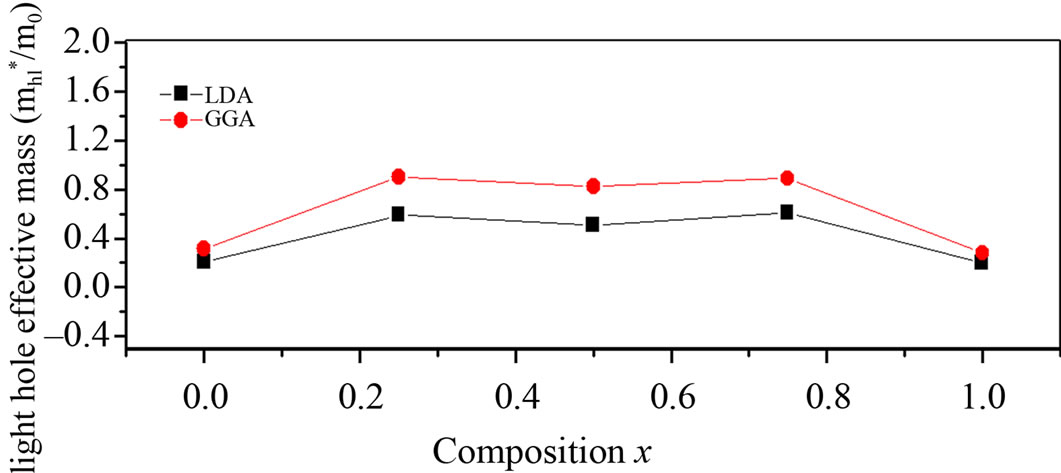
Theoretically, the effective masses can be estimated from the energy band curvatures. Generally, the effective mass is a tensor with nine components, however for the much idealized simple case, where the E-k diagram can be fitted by a parabola , the effective mass becomes a scalar at high symmetry point in Brillouin zone. We have computed the electron effective mass at the conduction band minima (CBM) and the hole effective mass at the valence band maxima (VBM) for BaS, BaSe and their ternary alloys, the results of our calculations were investtigated in Table 5, that shows the calculated electron and hole (heavy and light) effective masses for BaS1–xSex at point Γ of the Brillouin zone at various compositions, except for x = 0 and x = 1, where we calculated electron effective mass at point X of the Brillouin zone. Our results concerning the electrons, heavy holes and light hole effective mass are shown in Figure 5. From Table 5, we can outline that holes are much heavier than electrons, for all concentrations in BaS1–xSex alloy, the carrier transport in this alloy should be dominated by electrons. It is clearly seen that our LDA values for hole effective masses are smaller than the those using GGA, but the electrons effective mass values given by LDA are in good agreement with those using GGA.
, the effective mass becomes a scalar at high symmetry point in Brillouin zone. We have computed the electron effective mass at the conduction band minima (CBM) and the hole effective mass at the valence band maxima (VBM) for BaS, BaSe and their ternary alloys, the results of our calculations were investtigated in Table 5, that shows the calculated electron and hole (heavy and light) effective masses for BaS1–xSex at point Γ of the Brillouin zone at various compositions, except for x = 0 and x = 1, where we calculated electron effective mass at point X of the Brillouin zone. Our results concerning the electrons, heavy holes and light hole effective mass are shown in Figure 5. From Table 5, we can outline that holes are much heavier than electrons, for all concentrations in BaS1–xSex alloy, the carrier transport in this alloy should be dominated by electrons. It is clearly seen that our LDA values for hole effective masses are smaller than the those using GGA, but the electrons effective mass values given by LDA are in good agreement with those using GGA.
Table 5. Electron , light hole
, light hole  and heavy hole
and heavy hole 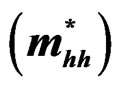 effective masses (in units of free electron mass m0) at the Γ point of the Brillouin zone of the ternary alloys under investigation compared with the available experimental and theoretical predictions.
effective masses (in units of free electron mass m0) at the Γ point of the Brillouin zone of the ternary alloys under investigation compared with the available experimental and theoretical predictions.
 (a)
(a)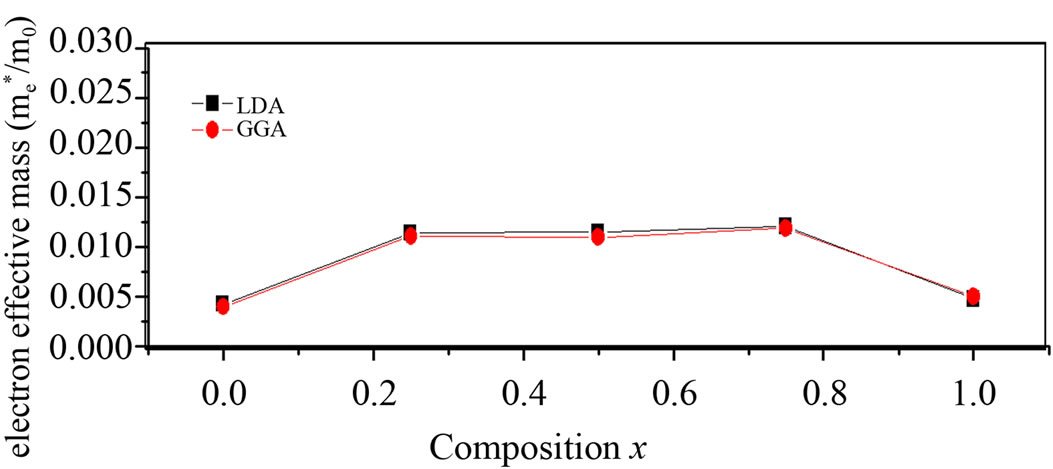 (b)
(b)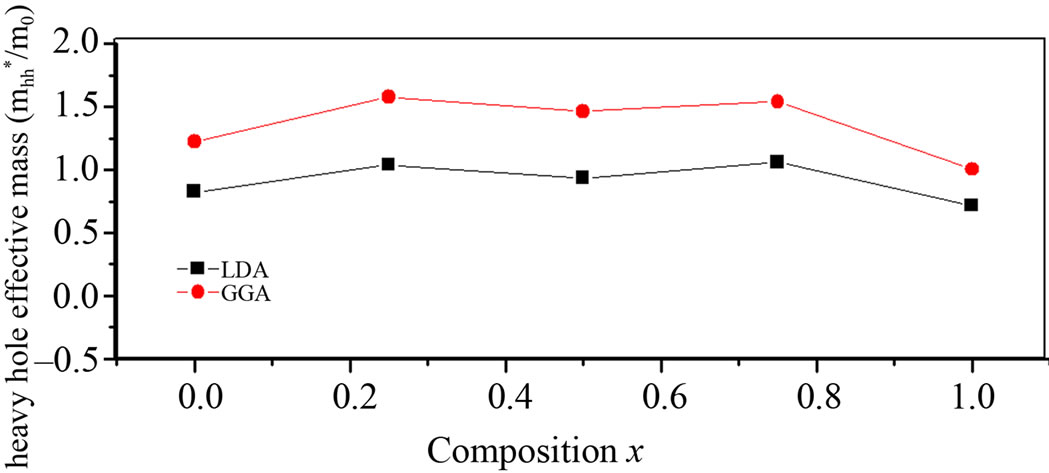 (c)
(c)
Figure 5. (a) Light hole effective mass at point Γ as function of Se composition within LDA and GGA; (b) Electron effective mass (in units of free electron mass m0) of Se composition within LDA and GGA; (c) Heavy hole effective mass at point Γ as function of Se composition within LDA and GGA.
4. Conclusion
We have used the FP-LMTO method within LDA and ment with the experimental data for structural properties. We observed that GGA somewhat overestimates the experimental data while LDA underestimates. For electronic band structure, our results with LDA and GGA, although in good agreement with other computational work, are lower than the experimental results. This is due to a simpler form of the exchange-correlation functional. The deviations of the lattice constant from Vegard’s law and bulk modulus from linear concentration dependence were observed for BaS1–xSex alloy. Our results show a strong dependence of the band gap bowing factor using Zunger approach on composition. The effective masses are investigated and showed good accordance using LDA and GGA especially for electron mass. To the best of knowledge .there are no earlier studies of the effective masses of electrons and holes of this compound; we feel that our calculations can be used to cover the lack of data for this compound.
5. Acknowledgements
This work has been achieved using FRGS Grant Nos.: 9003-00249 and 9003-00255. The author (Y.A.) would liketo acknowledge TWAS—Italy, for full support of his visitto JUST—Jordan under TWAS-UNESCO Associateship.
REFERENCES
- M. A. Haase, J. Qiu, J. M. DePuydt and H. Cheng, “BlueGreen Laser Diodes,” Applied Physics Letters, Vol. 59, No. 11, 1991, pp. 1272-1274. doi:10.1063/1.105472
- K. Syassen, N. E. Christensen, H. Winzen, K. Fischer and J. Evers, “Optical Response and Band-Structure Calculations of Alkaline-Earth Tellurides under Pressure,” Physical Review B, Vol. 35, No. 8, 1987, pp. 4052-4059. doi:10.1103/PhysRevB.35.4052
- G. Kalpana, B. Palanivel and M. Rajagopalan, “Electronic Structure and Structural Phase Stability in BaS, BaSe, and BaTe,” Physical Review B, Vol. 50, No. 17, 1994, pp. 12318-12325. doi:10.1103/PhysRevB.50.12318
- T. Y. Lv, D. Y. Chen and M. C. Huang, “Quasiparticle Band Structures of BaO and BaS,” Journal of Applied Physics, Vol. 100, No. 8, 2006, Article ID: 086103.
- Y. Kaneko and T. Koda, “New Developments in IIa-VIb (Alkaline-Earth Chalcogenide) Binary Semiconductors,” Journal of Crystal Growth, Vol. 86, No. 1-4, 1988, pp. 72-78.
- A. E. Carlsson and J. W. Wilkins, “Band-Overlap Metallization of BaS, BaSe, and BaTe,” Physical Review B, Vol. 29, No. 10, 1984, pp. 5836-5839. doi:10.1103/PhysRevB.29.5836
- Y. M. Kapoor and E. B. Hensley, “Jahn-Teller Effect on F Centers in Barium Sulfide,” Physical Review B, Vol. 23, No. 10, 1981, pp. 5581-5589. doi:10.1103/PhysRevB.23.5581
- A. Pourghazi and M. Dadsetani, “Electronic and Optical Properties of BaTe, BaSe and BaS from First Principles,” Physica B: Condensed Matter, Vol. 370, No. 1-4, 2005, pp. 35-45. doi:10.1016/j.physb.2005.08.032
- J. E. Bernard and A. Zunger, “Optical Bowing in Zinc Chalcogenide Semiconductor Alloys,” Physical Review B, Vol. 34, No. 8, 1986, pp. 5992-5995. doi:10.1103/PhysRevB.34.5992
- S. Savrasov and D. Savrasov, “Full-Potential Linear Muffin-Tin Orbital Method for Calculating Total Energies and Forces,” Physical Review B, Vol. 46, No. 19, 1992, pp. 12181-12195. doi:10.1103/PhysRevB.46.12181
- W. Kohn and L. J. Sham, “Self-Consistent Equations Including Exchange and Correlation Effects,” Physical Review A, Vol. 140, No. 4, 1965, pp. A1133-A1138.
- S. Y. Savrasov, “Program LMTART for Electronic Structure Calculations,” Zeitschrift für Kristallogr, Vol. 220, 2005, pp. 555-557. doi:10.1524/zkri.220.5.555.65067
- J. P. Perdew and Y. Wang, “Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy,” Physical Review A, Vol. 45, No. 13, 1992, pp. 13244-13249.
- J. P. Perdew, S. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868. doi:10.1103/PhysRevLett.77.3865
- P. Blochl, O. Jepsen and O. K. Andersen, “Improved Tetrahedron Method for Brillouin-Zone Integrations,” Physical Review B, Vol. 49, No. 23, 1994, pp. 16223- 16233. doi:10.1103/PhysRevB.49.16223
- F. D. Murnaghan, “The Compressibility of Media under Extreme Pressures,” Proceedings of the National Academy of Sciences of United States of America, Vol. 30, 1944, pp. 244-247. doi:10.1073/pnas.30.9.244
- Z. B. Feng, H. Q. Hu, S. X. Cui and W. J. Wang, “Electronic Structure Calculations for BaSxSe1−x Alloys,” Physica B, Vol. 404, 2009, pp. 2107-2110. doi:10.1016/j.physb.2008.11.201
- G. Q. Lin, H. Gong and P. Wu, “Electronic Properties of Barium Chalcogenides from First-Principles Calculations: Tailoring Wide-Band-Gap II-VI Semiconductors,” Physical Review B, Vol. 71, No. 8, 2005, Article ID: 085203.
- S. H. Wei and H. Krakauer, “Local-Density-Functional Calculation of the Pressure-Induced Metallization of BaSe and BaTe,” Physical Review Letters, Vol, 55, No, 11, 1985, pp. 1200-1203.
- S. Yamaoka, O. Shimomuro, H. Nakasawa and O. Fukunaga, “Pressure-Induced Phase Transformation in BaS,” Solide State Communications, Vol. 33, No. 1, 1980, pp. 87-89.
- L. Vegard, “Formation of Mixed Crystals by Solid-Phase Contact,” Journal of Physics, Vol. 5, No. 5, 1921, pp. 393-395.
- B. Jobst, D. Hommel, U. Lunz, T. Gerharda and G. Landwehr, “E0 Band-Gap Energy and Lattice Constant of Ternary Zn1−xMgxSe as Functions of Composition,” Applied Physics Letters, Vol. 69, No. 1, 1996, pp. 97-100. doi:10.1063/1.118132
- F. El Haj Hassan and H. Akdarzadeh, “First-Principles Investigation of BNxP1−x, BNxAs1−x and BPxAs1−x Ternary Alloys,” Materials Science and Engineering, Vol. 121, No. 1-2, 2005, pp. 171-178. doi:10.1016/j.mseb.2005.03.019
- S. Drablia, H. Meradji, S. Ghemid, G. Nouet and F. El Haj Hassan, “First Principles Investigation of Barium Chalcogenide Ternary Alloys: Gap Bowing,” Computational Materials Science, Vol. 46, No. 2, 2009, pp. 376- 382. doi:10.1016/j.commatsci.2009.03.013
- A. Bouhemadou, et al., “Electronic Properties: Band Gap,” Computational Materials Science, Vol. 38, No. 2, 2006, pp. 263-270. doi:10.1016/j.commatsci.2006.03.001
- R. J. Zolweg, Physical Review, Vol. 11, 1958, p. 113.
- G. A. Saum and E. B. Hensley, “Fundamental Optical Absorption in the IIA-VIB Compounds,” Physical Review, Vol. 113, No. 4, 1959, pp. 1019-1022. doi:10.1103/PhysRev.113.1019
- R. Khenata, M. Sahnoun, H. Baltache, M. Rérat, D. Rached, M. Driz and B. Bouhafs, “Structural, Electronic, Elastic and High-Pressure Properties of Some AlkalineEarth Chalcogenides: An ab Initio Study,” Physica B, Vol. 371, 2006, pp. 12-19.
- P. Dufek, P. Blaha and K. Schwarz, “Applications de Engel et le Rapprochement de Vosko Gradient Généralisé Dans les Solides,” Physical Review B, Vol. 50, No. 11, 1994, pp. 7279-7283.
- G. B. Bachelet and N. E. Christensen, “Relativistic and Core-Relaxation Effects on the Energy Bands of Gallium Arsenide and Germanium,” Physical Review B, Vol. 31, No. 2, 1985, pp. 879-887.
- G. Onida, L. Reining and A. Rubio, “Electronic Excitations: Density-Functional versus Many-Body Green’sFunction Approaches,” Reviews of Modern Physics, Vol. 74, 2002, pp. 601-659. doi:10.1103/RevModPhys.74.601
- O. Zakharov, A. Rubio, X. Blase, M. L. Cohen and S. G. Louie, “Quasiparticle Band Structures of Six II-VI Compounds: ZnS, ZnSe, ZnTe, CdS, CdSe, and CdTe,” Physical Review B, Vol. 50, No. 15, 1994, pp. 10780-10787. doi:10.1103/PhysRevB.50.10780
NOTES
*Corresponding author.

