Circuits and Systems
Vol.07 No.08(2016), Article ID:67122,11 pages
10.4236/cs.2016.78105
System-on-Chip Test Data Compression Based on Split-Data Variable Length (SDV) Code
J. Robert Theivadas1*, V. Ranganathan2, J. Raja Paul Perinbam3
1Department of ECE Research Scholar, Anna University, Chennai, India
2Department of ECE, Vignan University, Guntur, India
3Department of ECE, KCG College of Technology, Chennai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 April 2016; accepted 13 May 2016; published 6 June 2016
ABSTRACT
System-on-a-chips with intellectual property cores need a large volume of data for testing. The large volume of test data requires a large testing time and test data memory. Therefore new techniques are needed to optimize the test data volume, decrease the testing time, and conquer the ATE memory limitation for SOC designs. This paper presents a new compression method of testing for intellectual property core-based system-on-chip. The proposed method is based on new split- data variable length (SDV) codes that are designed using the split-options along with identification bits in a string of test data. This paper analyses the reduction of test data volume, testing time, run time, size of memory required in ATE and improvement of compression ratio. Experimental results for ISCAS 85 and ISCAS 89 Benchmark circuits show that SDV codes outperform other compression methods with the best compression ratio for test data compression. The decompression architecture for SDV codes is also presented for decoding the implementations of compressed bits. The proposed scheme shows that SDV codes are accessible to any of the variations in the input test data stream.
Keywords:
Test Data Compression, SDV Codes, SOC, ATE, Benchmark Circuits

1. Introduction
One of the important objectives of detailed testing of VLSI (very large scale integration) circuits and systems is to make sure that there are no defects in the manufactured products, and that they meet the specifications. Further, the information generated during the testing may come of help in increasing the product yield via improvising the process technology by reducing the production cost.
The fabrication process of the integrated circuit has different steps including photolithography, printing, etching and doping. During manufacturing, each of these steps has its own flaws. These flaws may lead to failure in the operation of the individual ICs. VLSI technology has made the testing of ICs complex and time consuming resulting in the increased cost of the ICs. The problems related to testing have enormously intensified in case of SOC (System on Chip) because of the large numbers of IP (Intellectual Property) cores on a single silicon chip. This huge reduction in the circuit size has increased the sensitivity to performance variations and they still require complete testing before they are shipped to the customers. There is no denying of the fact that the overall quality of the final product is greatly improved through testing, though it has no bearing on the manufacturing caliber of the ICs. The testing ensures the imperfections of the product are detected only if it is implemented during the crucial stages of the development cycle. It can also be taken as an approach to validate the design and check the process involved.
The different IP cores of a SOC are not readily accessible because of the complexity of the SOC and inadequate test pins. However, one can increase the accessibility of a controllable or observable node in the circuit by applying the DFT (Design-For-Testability) strategies. These strategies decrease the test cost, increase the product’s quality, and make easy the design characterization and test program implementation. In order to test these systems effectively, each IP core must be exercised duly with the core vendor’s set of established test patterns. In case of VLSI systems, due to higher storage requirements for fault-free responses, the traditional test processes become quite expensive. Alternate approaches are pursued in order to reduce the test data volume or the amount of storage required.
A design methodology called BIST (Built-in-Self-Testing) [1] - [3] is capable of providing solutions to numerous problems faced in testing digital systems. In order to test a SOC, the test patterns are initially generated and stored in an exclusive computer. The increase in the different types of SOCs has increased the requirement for the numbers of test patterns and also the frequent downloading of these test patterns into an ATE (Automatic Test Equipment). The size of these test patterns can be quite large that it may require a lot of time for downloading an ATE. However, the data memory, input-output channel capacity, and speed of traditional ATEs are limited. These machines are also quite expensive. Because of this, newly developed compression techniques are expected to decrease testing time and storage capacity.
The emergence of new test vector compression techniques [4] [5] and data compression in SOC techniques (SOC containing an embedded processor core) [6] [7] has been recently reported. Embedded processor has significantly increased Soc design flexibility, lengthened SOC product lifetime, and reduced design errors by permitting the devices to adapt to evolving standards and by allowing the addition of extra features over time [8] . Therefore, the compression technique must not only be efficient enough to decrease the test data volume, but also effective enough in its decompression. Various techniques have been proposed in the literature for compressing test data and their decompression. The Test sets are compressed using the selective Huffman coding is presented in [9] assuming full scan circuits and allowing reduction of hardware overhead of Huffman FSM. The Test data is encoded by using nine-types of codeword, Nine-Coded Compression based on fixed to variable coding scheme. The drawback of the method is the increased length of symbol. Other methods are presented based on Frequency-Directed Runlength (FDR) [10] , Golomb Codes, Variable-input Huffman coding (VIHC), Lempel-Ziv-Welch (LZW) Coding [12] , Associative Coder of Buynovsky (ACB) [11] , Run Length Coding (RLC), Burrow-Wheeler Transform (BWT) [14] , Variable to Variable Huffman code and Tunstall coding. Compression techniques are proposed in order to reduce test data volume. In [10] , the test vectors are compressed as difference vectors Tdiff from Original Test vectors TD and this leads to the reduction of testing time and smaller test sets.
In this paper, a new technique has been presented for efficient implementation of test data compression and decompression for system-on-a-chip designs. This paper introduces a new class of variable length compression codes that are designed using the split-options along with identification bits of string of test data.
2. Proposed Methodology
2.1. SDV Codes
The Split-data algorithm technique approach is to split-off the data from a string of test data vector in order to achieve compressed bits in the form of variable-length codes. The Simple Run-length code for remaining higher order bits contains a run of “0 s” which is equal to the decimal value of the higher order bits. Digit “1” is deployed after a sequence of “0 s”. For Example, Simple Run Length code is shown in Table 1 by using some of the code word. The Bth split-option splits the code word into LSB and MSB, whereas LSB splits-off based on the value of B. In case, if B split bit is 0 then it results in no split-bit of LSB, Incase B split bit is 1, one bit from LSB splits-off, if B split bit is 2, two bits from LSB splits-off and remaining higher order bits are encoded to a run length codes. In this paper, the Bth split-option is extended up to value of B = 7, since each of the code word is taken as 8 bits and each of the split-option results in the reduction of the number of bits. Table 2 shows the Split-options using simple Run-Length Codes (RLC). Test vectors considered in Table 2 are analyzed for each B value by using the concept of split-data. For example, in the code word 00001111, since there is no data split for B, B = 0 so only the RLC is performed. This results in some compression. For B = 1, 1 LSB splits-off and remaining higher bits are encoded into 7 zeroes + 1. After concatenation of LSB and RLC, the total number of bits is 9 (1LSB + RLC- > 1 + 7 zeroes + 1). For B = 2, 2 LSB splits-off and so RLC is performed as 3 zeroes + 1 resulting in 6 bits (2LSB + RLC- > 11 + 3 zeroes + 1). In order to know highest reduction of bits from all the B split-option, the overall number of bits in each B split option has to be added. The reduction of the number of bits for each split B option is seen in Table 2. This is made up to B = 7. To find highest compressed bits, in each and every split-option total number of compressed bits must be added from all the code words. In Table 2, the total number of compressed bits for B = 0 is 518 bits, B = 1 is 201 bits, B = 2 is 114 bits, B = 3 is 74 bits, B = 4 is 58 bits and finally B = 5 is 55 bits. By comparing all the total number of compressed bits for all the values of B, the highest compression is achieved in B = 5 with 55 bits. This result in a higher reduction of bits compared to other values of B. From Table 2, B = 5 will achieve the data reduction from the original 64 bits to 55 bits. In this case, B = 5 will be selected. The split-option achieving the highest compression is selected to identify the option to the decoder.
2.2. Block Diagram and Algorithm of Proposed Method
Figure 1 shows the block diagram of the proposed technique. The Test vectors required for testing an SOC are compressed in software mode. The Execution of the decompression program allows recovering the uncompressed original test vectors and then these test vectors are applied to each and every core of the SOC to analyze the output responses. The Test vectors provided by core vendor are divided into 8 bits of equal size and the size of the block depends on the total number of bits in each vector. The Block selection is divided into several blocks of equal size based on the total number of bits. In this paper, the number of bits for each block is an 8bit code word and the total number of blocks presented here is 8 blocks in parallel i.e. B = 0 to B = 7.
The selection of the blocks is made on the basis of giving ID bit pattern that the selected option will use to split the LSB and encodes remaining higher order bits of current block of samples. An ID bit sequence specifies the selection of option to encode the set of code words. With the same ID bits, the decoder is used for partial implementations of encoded bits. At last, ID bits and concatenation of the LSB and RLC is encoded to generate encoded test data TE. This results in limited memory, whereas original test vectors results in high memory for storage. The Overall concept of SDV compression is shown in Algorithm 1. At the initial stage, test vectors are generated along with ID bits, this allows to select any one of the split-option and this is repeated until TD has
Table 1. Run length code.
Table 2.Split-options using simple Run Length Codes(RLC).
Figure 1. Block diagram of proposed method.
binary values. (Table 3)

Figure 2 describes the overall concept of decompression to recover the original test vectors. The encoded bits
Figure 2. Conceptual architecture of decompression.
are decoded with presence of ID bits, to select any one of the blocks based on ID bits. To convert to 8 bit code word, counters are used to count number of 0s until it reaches 1. These numbers of 0s are transferred to code word and finally LSB and converted code word is concatenated to result in the original uncompressed test vector. Algorithm 2 describes the overall concept of decompression to achieve the original uncompressed bits.

3. Results of Simulation Experiments
Test vector generation program was employed to obtain a set of test vectors to provide 100% fault coverage, MINTEST. The percentage of data compression is computed based on
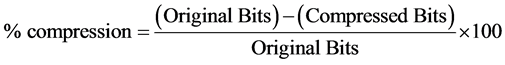 (1)
(1)
The experimental results are shown in Tables 4-6 and Figures 3-5.
Table 4 and Table 5 show compression results obtained from ISCAS 85, ISCAS 89 combinational and sequential benchmark circuits. The scan size is also considered for combinational and sequential circuits and compression achieved is 80%. The column 4 illustrates the original size of test vectors and consequently remaining column shows the compression achieved for split options with various combinational and sequential circuits,
Table 3. Selection of identification bit pattern.
Table 4. Test vector compression percentage several ISCAS’85 benchmark combinational circuits using proposed technique pattern.
Table 5. Test vector compression percentage several ISCAS’85 benchmark sequential circuits using proposed technique pattern.
Table 6. Test vector compression ratio and time for both ISCAS 85 combinational circuits and ISCAS 89 sequential circuits.
Figure 3. Test vector compression results for several ISCAS 85 benchmark combinational circuits using proposed technique.
Figure 4. Test vector compression results for several ISCAS 89 benchmark sequential circuits using proposed technique.
Figure 5. Time taken to compress test data for ISCAS 85 and ISCAS 89 benchmark circuits (seconds).
which is extended up to a value of 7.
Finally, Figure 3 and Figure 4 graphically shows the test vector compression results for several ISCAS 85 and ISCAS 89 benchmark circuits using SDV coding for various values of B. The graphical diagram shows that the overall average percentage for both combinational and sequential circuits is 80. Table 6 describes the overall compression percentage and time taken to compress the test data under the proposed scheme. Figure 5 shows graphically the time taken to compress the test data in seconds for combinational and sequential circuits.
Table 7 shows the compression results obtained from ISCAS 85 and ISCAS 89 benchmark circuits with comparison of other compression techniques. The Highest compression is obtained compared to Huffman coding, Lempel-Ziv-Welch (LZW) Coding, Associative Coder of Buynovsky (ACB), Burrow-Wheeler Transformation (BWT) presented in Table 7. From the proposed technique, data compression is achieved mainly due to SDV technique in successive test vectors. Figure 6 shows the comparative results of various techniques along with proposed technique. From the comparative experimental results, the developed compression strategy provides better compression results than other various compression methods.
4. Conclusion
Since test data compression is the most important technique it must be lossless and effective. The compression
Figure 6. Test vector compression results for ISCAS 85 and ISCAS 89 Bench mark circuits using other compression methods and proposed technique.
Table 7. Test vector compression results for ISCAS 85 and ISCAS 89 bench mark circuits using other compression methods and proposed technique.
method herein is based on a Split-Data Variable length (SDV) coding technique that targets to split-off the bits to achieve compression. The technique SDV reduces the test vector sequences, and results in a higher compression ratio. The compression process is done before downloading the test vectors into the on-chip memory. The method proposed helps in reducing the test data and testing time. Further this method proposed herein is completely lossless because of its higher compression ratio.
Cite this paper
J. Robert Theivadas,V. Ranganathan,J. Raja Paul Perinbam, (2016) System-on-Chip Test Data Compression Based on Split-Data Variable Length (SDV) Code. Circuits and Systems,07,1213-1223. doi: 10.4236/cs.2016.78105
References
- 1. Reungpeerakul, T. and Kay, D. (2010) Partial-Matching Technique in a Mixedmode BIST Environment. IEEE Transactions on Instrumentation and Measurement, 59, 970-977.
http://dx.doi.org/10.1109/TIM.2009.2031458 - 2. Groza, V., Abielmona, R. and Assaf, M.H. (2007) A Self-Reconfigurable Platform for Built-in Self-Test Applications. IEEE Transactions on Instrumentation and Measurement, 56, 1307-1315.
http://dx.doi.org/10.1109/TIM.2007.900134 - 3. Kay, D., Chung, S. and Mourad, S. (2005) Embedded Test Control Schemes Using iBIST for SoCs. IEEE Transactions on Instrumentation and Measurement, 54, 956-964.
http://dx.doi.org/10.1109/TIM.2005.847349 - 4. Biswas, S., Das, S.R. and Petriu, E.M. (2006) Space Compactor Design in VLSI Circuits Based on Graph Theoretic Concepts. IEEE Transactions on Instrumentation and Measurement, 55, 1106-1118.
http://dx.doi.org/10.1109/TIM.2006.876523 - 5. Biswas, S. and Das, S.R. (2006) A Software-Based Method for Test Vector Compression in Testing System-on-a-Chip. IEEE Instrumentation and Measurement Technology Conference Proceedings, Sorrento, 24-27 April 2006, 359-364.
http://dx.doi.org/10.1109/imtc.2006.328472 - 6. Zuchowski, P.S., Reynolds, C.B., Grupp, R.J., Davis, S.G., Cremen, B. and Troxel, B. (2002) A Hybrid ASIC and FPGA Architecture. IEEE/ACM International Conference on Computer Aided Design, 10-14 November 2002, 187- 194.
- 7. Abramovici, M., Stroud, C. and Emmert, M. (2002) Using Embedded FPGAs for SoC Yield Improvement. Proceedings of the 39th Design Automation Conference, 10-14 June 2002, 713-724.
http://dx.doi.org/10.1109/dac.2002.1012717 - 8. Wilton, S.J.E. and Saleh, R. (2001) Programmable Logic IP Cores in SoC Design: Opportunities and Challenges. IEEE Conference on Custom Integrated Circuits, San Diego, 9 May 2001, 63-66.
http://dx.doi.org/10.1109/cicc.2001.929724 - 9. Jas, A., Ghosh-Dastidar, J., Ng, M.-E. and Touba, N.A. (2003) An Efficient Test Vector Compression Scheme Using Selective Huffman Coding. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 22, 797-806.
http://dx.doi.org/10.1109/TCAD.2003.811452 - 10. Chandra, A. and Chakrabarty, K. (2001) Frequency-Directed Run Length (FDR) Codes with Application to System-on- a-Chip Test Data Compression. Proceedings of the 19th IEEE VLSI Test Symposium, Marina Del Rey, May 2001, 42-47.
- 11. Skopal, T. (2002) ACB Compression Method and Query Preprocessing in Text Retrieval Systems. Proceedings of DATESO 2002, Desna, Czech Republic.
- 12. Ziv, J. and Lempel, A. (1997) A Universal Algorithm for Sequential Data Compression. IEEE Transactions on Information Theory, IT-23, 337-343.
- 13. Gonciari, P.T., Al-Hashimi, B.M. and Nicolici, N. (2003) Variable-Length Input Huffman Coding for System-on-a- Chip Test. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 22, 783-796.
http://dx.doi.org/10.1109/TCAD.2003.811451 - 14. Biswas, S.N., Das, S.R. and Petriu, E.M. (2014) On System-on-Chip Testing Using Hybrid Test Vector Compression. IEEE Transactions on Instrumentation and Measurement, 63, 2611-2619.
http://dx.doi.org/10.1109/TIM.2014.2313431
NOTES
*Corresponding author.










