Circuits and Systems
Vol. 3 No. 4 (2012) , Article ID: 23642 , 8 pages DOI:10.4236/cs.2012.34045
An Analytical Approach for Fast Automatic Sizing of Narrow-Band RF CMOS LNAs with a Capacitive Load*
Electronic & Electrical Engineering Department, Hongik University, Jochiwon, South Korea
Email: jychoi@hongik.ac.kr
Received July 19, 2012; revised August 19, 2012; accepted August 26, 2012
Keywords: Automatic Synthesis; Analytical Approach; CMOS LNA; Narrow Band; Cascode
ABSTRACT
We introduce a fast automatic sizing algorithm for a single-ended narrow-band CMOS cascode LNA with a capacitive load based on an analytical approach without any optimization procedure. Analytical expressions for principle parameters are derived based on an ac equivalent circuit. Based on the analytical expressions and the power-constrained noise optimization criteria, the automatic sizing algorithm is developed. The algorithm is coded using Matlab, which is shown capable of providing a set of design variable values within seconds. One-time Spectre simulations assuming usage of a commercial 90 nm CMOS process are performed to confirm that the algorithm can provide the aimed first-cut design with a reasonable accuracy for the frequency ranging up to 5 GHz.
1. Introduction
In the field of RF transceiver design, there is a strong demand to digitalize even RF analog parts to mount a transceiver on a single chip [1,2] to utilize the capability of automatic synthesis in digital circuit design. However, the low noise amplifier (LNA), which is a critical building block in any RF front-end, is not ready for digitalization yet. Many efforts have been done for design automation of LNA beforehand since the design of LNA is a time-consuming task that typically relies heavily on the experience of RF designers. LNA design automation can significantly simplify the design task, and also opens a possibility towards digitalization.
There are two basic methods for LNA design automation: simulation based or equation based. Although the simulation-based methods [3,4] are more accurate, they are time consuming due to optimization procedures. On the other hand, equation-based methods [5-7] are faster, but are dependent on the accuracy of the models used. To overcome the disadvantages in some extent, advanced methods using both of equation-based and simulationbased approaches [8-10] have been also suggested.
The difficulties in design automation of LNA lie in several aspects. It is topology dependent, and the design itself is difficult involving trade-offs among critical figures of merits such as NF, power gain, impedance matching, power consumption, linearity, and stability. It is desirable if the first-cut design synthesis can be done automatically and fast with an acceptable accuracy.
A methodology for providing a set of first-cut design variables with a reasonable accuracy for a narrow-band LNA with a resistive load was previously suggested [11].
The purpose of this work is to extend the above methodology to a narrow-band LNA with a capacitive load, which is frequently encountered in front-end design.
In this paper, based on an analytical approach without any optimization procedure, we introduce a speedy automatic sizing algorithm for a single-ended narrow-band cascode LNA adopting inductive source degeneration with a capacitive load. In Section 2, design assumptions are discussed. In Section 3, analytical expressions for principle parameters are derived based on an ac equivalent circuit assuming a capacitive output termination. In Section 4, the developed automatic sizing algorithm is explained. In Section 5, verifications are given to check the accuracy of the automatic sizing results.
2. Design Assumptions
The cascode structure with an inductive source degeneration shown in Figure 1 is chosen as the objective circuit for automatic sizing.
To avoid any confusion, we show the assumptions made in this work, which are same with those in [11].
1) Narrow-band LC matching networks are used for input and output as shown in Figure 1. R1 is used to provide capability for adjusting power gain. As the output termination, two cases are considered: resistive or capacitive termination.
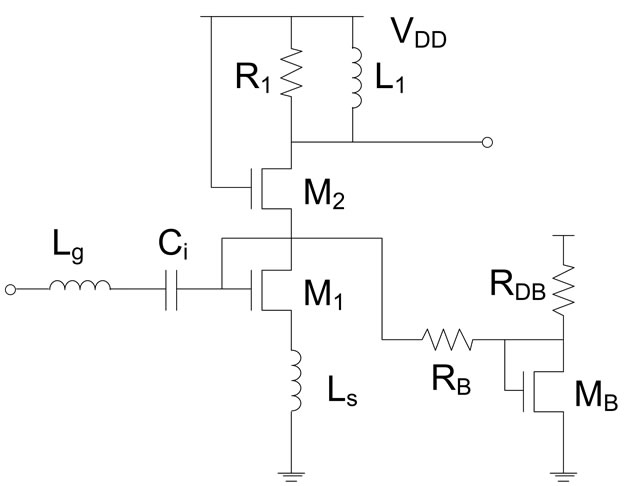
Figure 1. Assumed cascode LNA circuit.
2) For sizing of the MOS transistors M1 and M2, the power-constrained noise optimization (PCNO) criteria [12] is adopted to trade off noise performance against power consumption.
3) Ideal inductors and capacitors are used by assuming usage of off-chip components.
4) A current-mirror biasing is adopted as shown in Figure 1.
5) The widths of M1 and M2 are set as same.
6) The design specifications include operating frequency, input and output terminations, power consumption, power gain, and sufficiently low input and output reflection coefficients S11 and S22.
7) The design variables include Lg, Ls, L1, Ci, R1, RDB, and RB including the widths of M1, M2, and MB in Figure 1.
3. Derivation of Analytic Expressions for Principal Parameters
3.1. Input Impedance
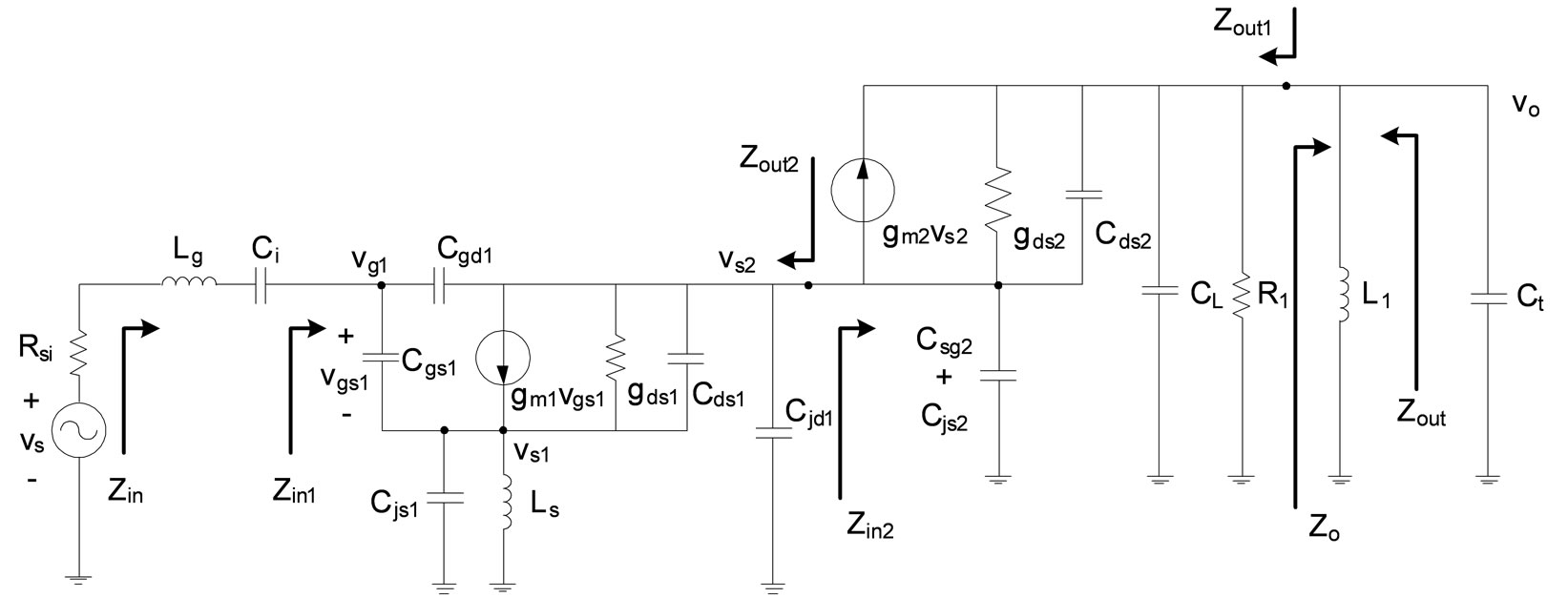
Figure 2 is the whole ac equivalent circuit for the cascode LNA shown in Figure 1 including the input signal source and the output capacitive termination Ct. We note that, compared to the complete equivalent circuit of the BSIM4 NMOS transistor in SPICE, only the back-gate transconductance gmb and the gate-body capacitance Cgb in the transistor model are ignored to simplify the analysis. The distributed resistances including Rs, Rd, Rg, and Rsub, which are included in the BSIM 4 transistor model, are also ignored since they are negligible in large transistors.
In Figure 2, gm1 and gm2 denote the transconductances of M1 and M2, respectively. Cgs, Cgd, and Cds denote the gate-source, gate-drain, and drain-source capacitances of the NMOS transistors, respectively. Cjs and Cjd denote the source-body and drain-body junction capacitances, and CL is equal to the sum of Cdg2 and Cjd2, which are the capacitances present at the drain node of M2 in Figure 1.
The impedances Zin, Zin1, Zin2, Zo, Zout, Zout1, and Zout2 are self-defined in the circuit. We note that Cgs, Cgd, and Cds are replaced by Csg, Cdg, and Csd, respectively, in some part of our derivations for input and output impedances considering the non-reciprocal nature of gate-oxide capacitances in the BSIM4 MOSFET capacitance model [13].
First, we derive Zin by deriving Zo, Zin2, and Zin1 in order. We note that, we use s and jω without differentiation since we are dealing with ac response only.
Yo = 1/Zo is simply expressed as
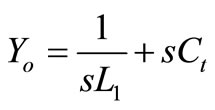 (1)
(1)
Following the same procedure in deriving Yin2 = 1/Zin2 in [11], we get the same Yin2 expression as
 , (2)
, (2)
where 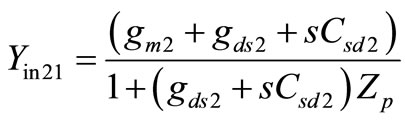
and Zp=(1/sCL)//R1//Zo.
Following the same procedure in deriving Yin1 = 1/Zin1 in [11] again, we get the same Yin1 expression as
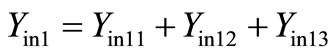 , (3)
, (3)
where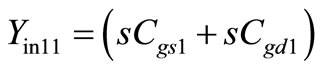 ,
,
 ,
,
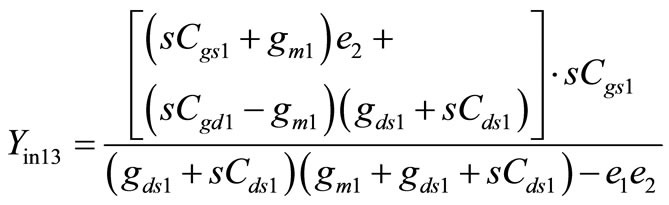 ,
,
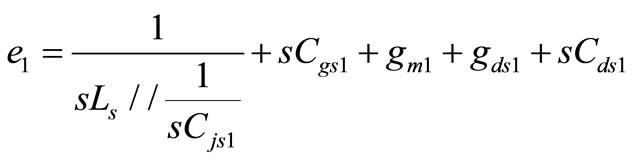 ,
,
 and ZL = (1/(sCjd1))//Zin2.
and ZL = (1/(sCjd1))//Zin2.
Then Zin is expressed as
 . (4)
. (4)
3.2. Output Impedance
Zout derivation can be done similarly as the Zin derivation using the equivalent circuit in Figure 2 assuming Rsi input termination. We present the results here, which are same with those presented in [11].
Yout2 = 1/Zout2 is expressed as
 , (5)
, (5)
where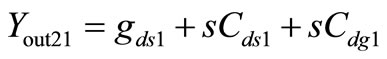 ,
,
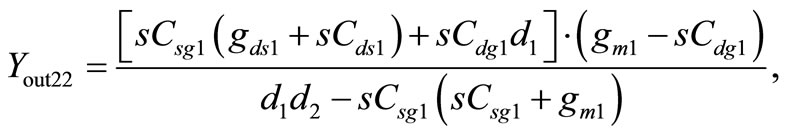
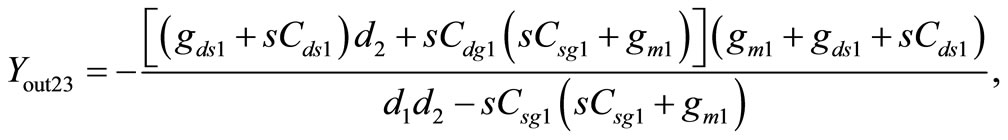
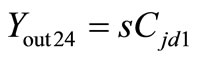 ,
,
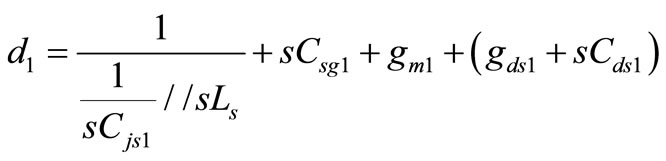 ,
,
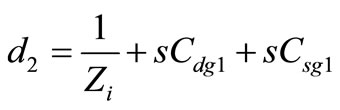 and
and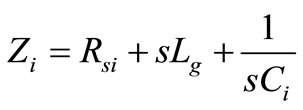 .
.
Yout1 = 1/Zout1 is expressed as
 , (6)
, (6)
where 
and .
.
Then Zout is expressed as
 . (7)
. (7)
3.3. Power Gain
To derive the LNA voltage gain, the equivalent circuit in Figure 2 is simplified into the one shown in Figure 3, where the whole circuit is expressed as a 3-stage cascaded amplifier.
Zin1, Zin2 and Zo in Figure 3 are already derived in (3), (2) and (1), respectively. Notice that A1vg1, gZout2, A2vs2, and gZout1 are the Thevenin equivalent voltages and impedances of the 2nd and 3rd gain stages in Figure 2.
The derivation procedures and the expressions are exactly same with those in [11]. Here we show the expressions.
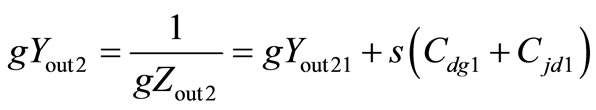 (8)
(8)
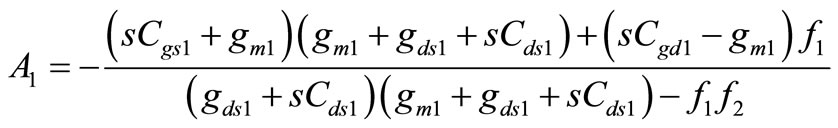 (9)
(9)
where 
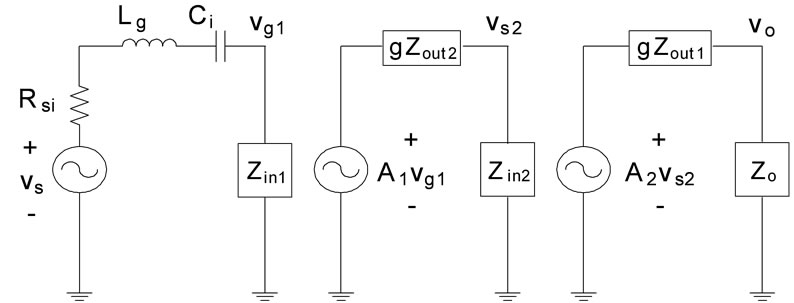
Figure 3. Equivalent circuit to find the voltage gain.
and .
.
 (10)
(10)
 (11)
(11)
In Figure 2, the available input power Pi, which is supplied to the LNA when impedance matched, is defined as
 . (12)
. (12)
In a capacitive load case, we can derive the available power gain by assuming an additional imaginary load ZL connected to the vo node in Figure 3. In this situation, the impedence Zpp seen by ZL is equal to gZout1//Zo. When , the maximum power Po can be transferred to the load. If we define RL and Rpp are the real parts of ZL and Zpp, respectively, then Po can be expressed as
, the maximum power Po can be transferred to the load. If we define RL and Rpp are the real parts of ZL and Zpp, respectively, then Po can be expressed as
 . (13)
. (13)
Then the available power gain G is expressed as
 (14)
(14)
where Av1, Av2, and Av3 can be easily derived from Figure 3 as follows.
 (15)
(15)
 (16)
(16)
 (17)
(17)
4. Automatic Sizing Algorithm
Figure 4 shows the automatic sizing algorithm developed in this work. Here, we explain the procedures from top to bottom.
4.1. 1st Step: Entering Design and Process Specifications
The 1st step in the automatic sizing is to enter the design and process specifications. The design specifications
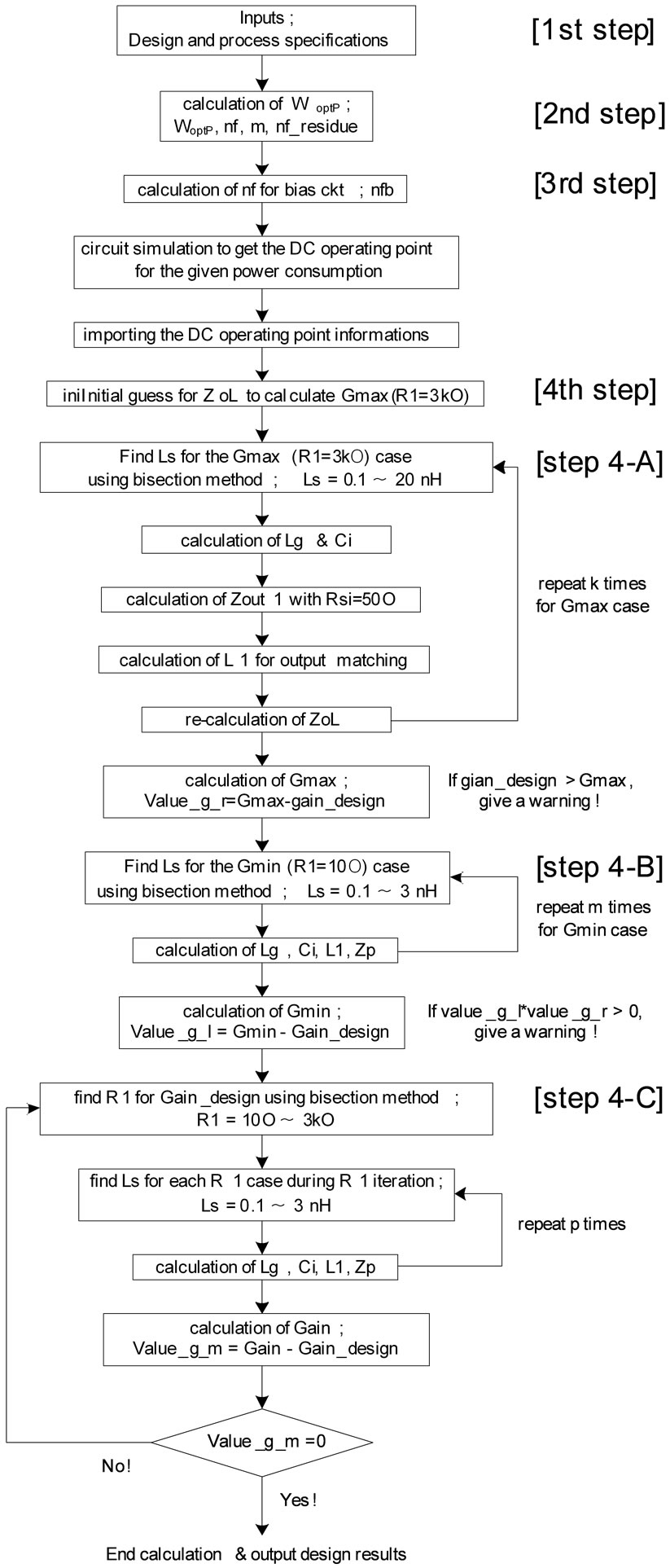
Figure 4. Automatic sizing algorithm.
include the operating frequency f, the input output terminations Rsi and Rso, the supply current IDD, the desired power gain Gain_design. Instead of IDD, the power consumption PWR and the supply voltage VDD can be entered to calculate IDD by PWR/VDD. The process specifications include the transistor channel length L, the transistor channel width per finger WF, and the maximum finger number nf_max defined for one unit of transistors.
4.2. 2nd Step: Calculation of Optimum Transistor Width
The next step is to calculate the transistor channel width W for optimum noise performance. The power-constrained noise optimization device width WoptP [12] is adopted as W in this work. WoptP is calculated according to the last rough equation in (18).
 (18)
(18)
As shown in (18), WoptP increases continuously as the frequency decreases. Therefore it may be necessary to define a maximum value for W considering lower frequency design. We suggest to limit W below 1000 μm.
If WF and nf_max are defined, the finger number nf is first calculated as W/WF, and the number of the maximum-fingered units m is calculated as the integer value of nf/nf_max, and the residual finger number nf_residue is determined as the residue to give an information for the transistor layout. Then the final W is determined by W = WF × (m × nf_max + nf_residue). We note that WF and nf_max are usually defined in most of recent processes.
4.3. 3rd Step: Calculation of Bias Circuit Design Variables and Getting DC Operating Point
The next step is to determine the bias circuit variable values and to get the dc operating point information.
The finger number for the bias transistor nfb and the drain bias resistance RDB in Figure 1 should be determined. By limiting the bias circuit current around 100 μA, for example, we can determine nfb by nfb = (100 μA/IDD) × nf. For the decoupling resistor RB, we can simply use 5 kΩ, which is a reasonable value.
The next procedure is to determine RDB, which, however, is very difficult to determine by calculation. Since IDD is sensitive to the value of RDB, it should be manually determined to give the specified IDD value by dc circuit simulations. This procedure is one obstacle against full design automation in this work. However, it is an essential procedure since it provides the accurate operating point information to proceed with the remaining part of the design automation. The needed operating point information include the values of gm, gds, Cgs, Csg, Cgd, Cdg, Cds, Csd, Cjs, and Cjd of M1 and M2 in Figure 1, which should be imported into the automatic sizing algorithm.
4.4. 4th Step: Iterations to Determine Design Variable Values
There are three main iteration loops in the automatic sizing algorithm as shown in Figure 4. The 1st loop finds Gmax, which corresponds to the case with the upper limit of R1, which is chosen arbitrarily large enough as 3 kΩ in this work. We note that this value is smaller than 10 kΩ compared to the 50 Ω resistive load case in [11] since it is easier to get a higher gain in the capacitive load case. To find Gmax, we need to find all the design variable values for the Gmax case simultaneously. Iteration is needed since the input and output matching designs affect each other. The 2nd loop finds Gmin, which corresponds to the case with the lower limit of R1, which is arbitrarily chosen small as 10 Ω in this work to allow a larger allowable gain range. This iteration is also needed for the same reason explained for the Gmax case. The 3rd loop finds the proper R1 value for the desired gain Gain_design by the bisection method, which lies within the lower and upper boundaries Gmin and Gmax, and its inner loop finds the corresponding design variable values for the present gain value during iteration similarly as in the 1st and 2nd iteration loops.
A. Iterations to Solve for the Gmax Case
As explained above, Zin1 is affected by output matching design, and Zout is affected by input matching design. Therefore we need some iteration to determine Ls. Since Zin2 is affected by Zo, which is unknown yet, we need an initial guess for Zo to find the 1st Ls value. As shown in Figure 4, an initial guess for ZoL = Zo//(1/sCL) is given as 200/gm2, which is shown to be large enough for all possible situations in the procedure, to solve for Zin2 by (2). We note that the initial guess is much larger than that for the resistive load case, which is due to the larger magnitude of the output node impedance.
The impedance seen at the gate of M1 is equal to Zin1, which is derived in (3). By setting the real part of Zin1 Re(Zin1) equal to Rsi for input impedance matching, we can find Ls. However this equation Re(Zin1) = Rsi is too complicated to get the solution directly with the other present design variables values given, and therefore Ls is solicited numerically within the lower and upper boundaries of 0.1 nH and 20 nH. We use the bisection method for this purpose.
The next procedure is to calculate Lg and Ci, which nullify the imaginary part of Zin1 Im(Zin1) in Figure 2. Zin1 is usually capacitive to give a negative value for Im(Zin1), and therefore Lg can be calculated using the equation Im(Zin1) − 1/(ωCi) + ωLg = 0, where Ci is simply a large dc blocking capacitor. We first calculate Lg1, which nullifies Im(Zin1) using Im(Zin1) + ωLg1 = 0. Although Ci is larger the better, considering the layout size, 1/(ωCi) = ωLg1/10 is used to determine Ci. Lg is then recalculated using Im(Zin1) − 1/(ωCi) + ωLg = 0.
Depending on to the operating frequency and the desired gain, Zin1 may happen to be inductive, or this situation can happen in the middle of the iterations. For this case, a nominal single bond wire inductance of 1 nH is assumed for Lg and Im(Zin1) − 1/ωCi + ωLg = 0 is used to calculate the required Ci value.
In the next procedure, the design variable L1 should be determined, which gives rise to a maximum gain.
The total admittance YY at the output (vo) node in Figure 2 is equal to Yout1 + 1/(sL1) + sCt. By recognizing a maximum voltage output is obtained at the output resonance condition, the required L1 value is the one which gives rise to a zero imaginary value of YY. This ends up with the L1 expression as
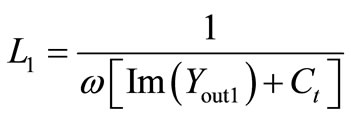 . (19)
. (19)
Now the 1st set of the design variable values are ready to update ZoL and the remaining iterations are performed to find the final design variable values for the Gmax case. It was found that the iteration number for this loop should be larger than 10.
Right after the iteration loop, A1, gZout2, A2, and gZout1 are calculated using (9), (8), (11), and (10), respectively, and Gmax is calculated using (14).
If the Gmax value is smaller than the desired gain, the routine gives a warning and stops.
B. Iterations to Solve for the Gmin Case
The 2nd loop finds the design variable values for the Gmin case. The same iteration as above with the last ZoL value as an initial guess is performed to find Gmin using (14) again.
C. Iterations to Solve for the Gain_design Case
The 3rd loop finds the proper R1 value for the desired gain Gain_design using the bisection method while the inner loop finds the corresponding design variable values for the present gain value. This inner iteration loop is exactly same as the 1st and 2nd loops. After all the design variables are determined for the present gain value, the gain is calculated using (25) again. If the calculated gain is equal to Gain_design within the allowed tolerance, the calculation stops to output the final set of the design variable values, which include W, nf, m, nf_residue, nfb, Ls, Lg, Ci, R1, and L1.
5. Verifications
The automatic sizing algorithm explained in Section 4 was coded using Matlab (Version 7.9.0.529) assuming usage of a 90 nm commercial CMOS process. The design variable sets for seven different operating frequencies ranging from 0.5 GHz to 5 GHz were synthesized, and verifications were done by one-time Spectre circuit simulations with the corresponding BSIM4.5.0 MOSFET model [13] for the assumed process.
The process specifications include L = 75 nm, WF = 3 μm, and nf_max = 64, where 75 nm for L is the effective channel length in this process. The maximum transistor width was set as Wmax = nf_max × m × WF = 64 × 5 × 3 μm = 960 μm, which is below 1000 μm as we suggested.
When the output is terminated by a capacitor, we encounter a difficulty to monitor the output matching and power gain in measurement. Therefore it is customary to connect a dummy source follower output stage for measurement purpose as shown in Figure 5. We note that the situation of the output node of M2 in this case is similar to the one in an LNA connected directly to a mixer in a same chip, which is the capacitive load case we are discussing here. Therefore, for the simulation setup for verification, we also added the source follower to monitor the output matching and power gain as shown in Figure 5. The output impedance of the source follower was adjusted to around 50 Ω regardless of the operating frequency, which is same with the assumed value of Rso. The dc blocking capacitor at the output was set very large as 1000 pF to eliminate any effect on the circuit in simulations.
To select the design specification value for Ct, we monitored the admittance Y11 seen at the input of the source follower in Figure 5 by circuit simulations, which were done separately but maintaining the same bias point setup and the same output termination as those in the whole circuit simulation. Table 1 shows the calculated parallel resistance and capacitance values calculated from the simulated Y11 values for the frequency range from 0.3 GHz to 5 GHz. From the results in Table 1, we concluded that the equivalent circuit of the source follower can be approximated by a simple capacitor of 93 fF since the parallel Rp values are large enough with fortune.

Figure 5. LNA circuit for verification in case of the capacitive output termination.
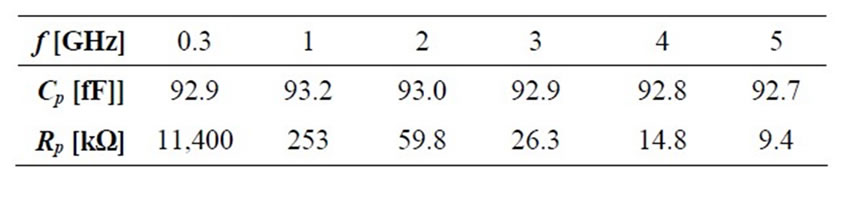
Table 1. Equivalent parallel R and C values of the source follower stage in Figure 5 as a function of frequency.
This situation coincides with the design objective we are focusing on here, which is the design of LNA with a capacitive load.
Verifications were done with the same automatic sizing algorithm explained in Section 4.
Design specifications include ID = 5 mA, VDD = 1.2 V, Gain_design = 25 dB, Rsi = 50 Ω, and Ct = 93 fF. We ignored the loss in the source follower stage to regard S21 of the whole circuit as the power gain of the LNA without the source follower. Therefore we can expect the power gain will be slightly larger than the simulated S21 values.
We did not include the power consumed in the source follower stage as the total power consumption since it is used only for measurement purpose.
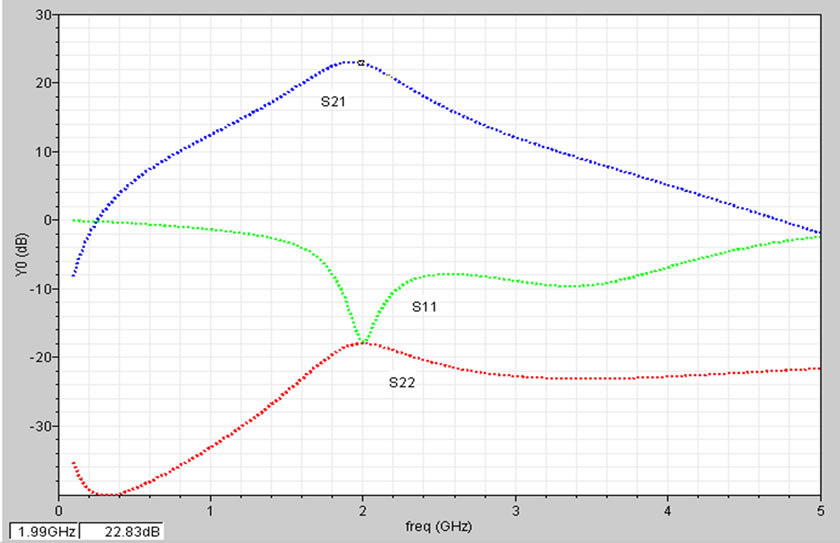
As an example of the verifications, Figure 6 shows the simulated LNA characteristics without any tuning for the operating frequency of 2 GHz, when the corresponding set of the design variable values obtained using the automatic sizing algorithm are used for the simulation. The synthesized design variable values are RDB = 9.9 kΩ, W = 576 μm (m = 3, nf_residue = 0), nfb = 4, Ls = 1.4693 nH,
 (a)
(a)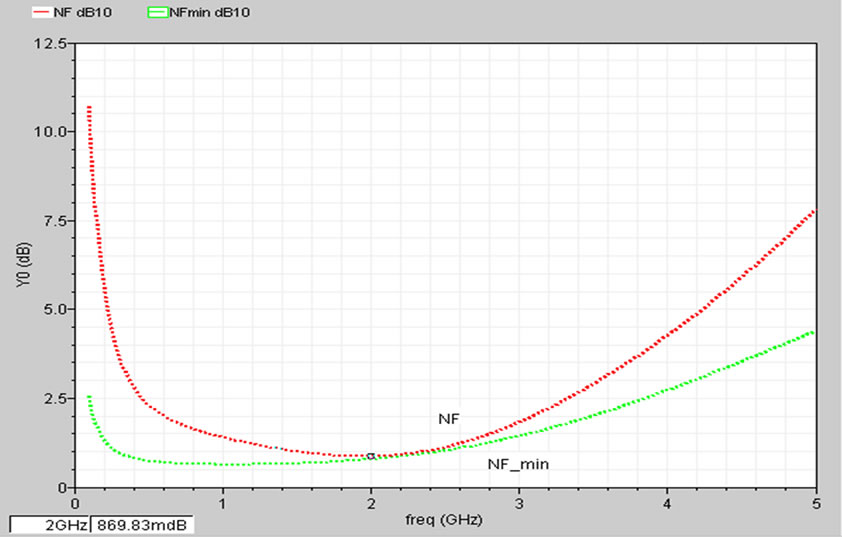 (b)
(b)
Figure 6. Simulated (a) S parameter and (b) Noise characteristics for f = 2 GHz and Gain_design = 25dB: S21 = 22.74 dB, NF = 0.870 dB, NFmin = 0.790 dB, S11 = −17.8 dB, S22 = −18.0 dB.
Lg = 6.868 nH, Ci = 10.14 pF, R1 = 631.4 Ω, and L1 = 11.713 nH. As expected with the source follower output stage adopted, S22 stays low for the whole frequency range.
Table 2 summarizes the simulated results of the designs for for Gain_design of 25dB for the frequency range from 0.5 GHz to 5 GHz.
In Table 2, the loss in the source follower seems negligible as desired, which is evident from the result for the 0.8 GHz design. We can see that the input and output matchings are reasonably good in the lower frequencies, but is not good enough in the higher frequencies, especially in the output matching. This may be caused by approximating the equivalent circuit of the source follower by a single capacitor of 93 fF in the syntheses by neglecting the smaller parallel resistance in higher frequencies shown in Table 1. If this is the case, we can say this discrepancy is caused by assigning the load improperly, which is not related to the adequacy of the synthesis algorithm. The S21 values in Table 2 are smaller than the desired gain of 25 dB in the higher frequency range. However we believe that the result is pretty good for the first-cut quick design.
Table 3 summarizes the synthesized available gain ranges with the corresponding R1 values for each design. For the operating frequency below 1 GHz, the synthesized device width is constrained as 960 μm, which is set as maximum, and decreases with frequency as expected.
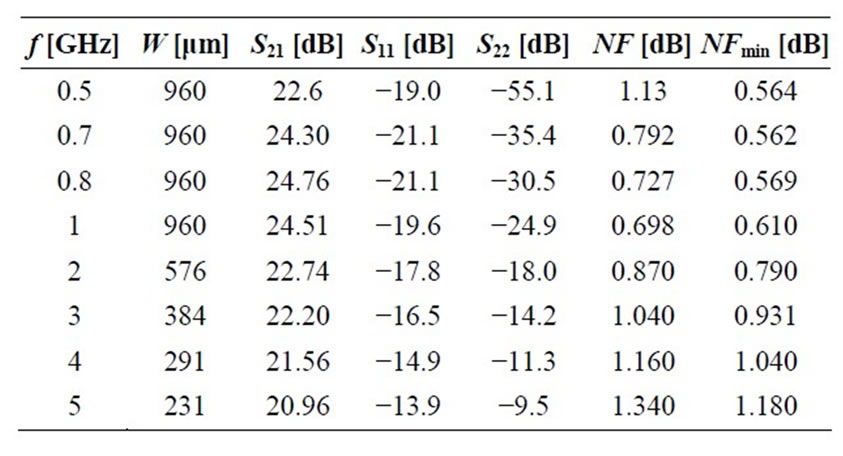
Table 2. Simulation summary for the desired gain Gain_ design of 25 dB.
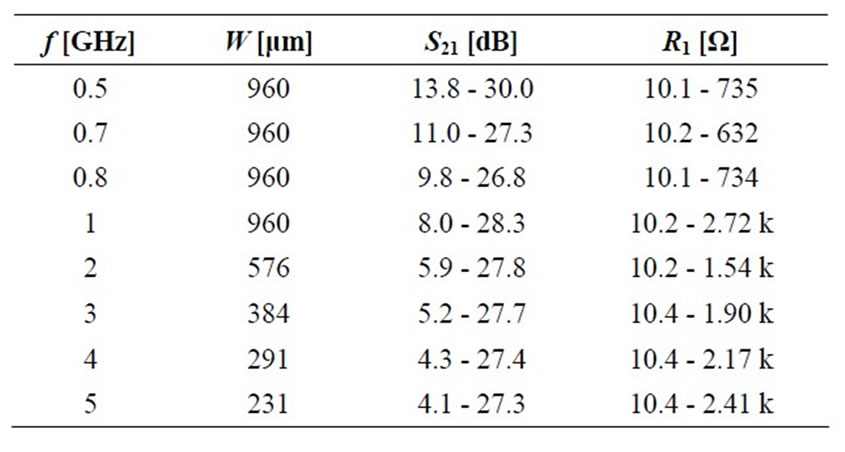
Table 3. Synthesis summary for the available gain ranges with the corresponding R1 values.
6. Conclusions
The analytical expressions for the principle parameters were derived using the ac equivalent circuit of the single-ended narrow-band cascode CMOS LNA with a capacitive load. Based on the expressions, the automatic sizing algorithm was developed by adopting the powerconstrained noise optimization criteria. The algorithm was coded using Matlab, and could provide a set of design variable values within seconds. One-time Spectre simulations without any tuning assuming usage of a commercial 90 nm CMOS process were performed to confirm that the automatic sizing program can synthesize the aimed first-cut design with a reasonable accuracy for the frequency range reaching up to 5 GHz.
This work showed in detail how the accurate automatic sizing can be done in an analytical approach. The approach can be applied to a common source LNA more easily since the derivation of principal parameters will be simpler with a fewer gain stages. It can be also applied to a differential LNA easily since the derivation will be basically same.
REFERENCES
- K. Muhammad, R. B. Staszewski and D. Leipold, “Digital RF Processing: Toward Low-Cost Reconfigurable Radios,” IEEE Communications Magazine, Vol. 43, No. 8, 2005, pp. 105-113. doi:10.1109/MCOM.2005.1497564
- A. A. Abidi, “The Path to the Software-Defined Radio Receiver,” IEEE Journal of Solid-State Circuits, Vol. 42, No. 5, 2007, pp. 954-966. doi:10.1109/JSSC.2007.894307
- G. Zhang, A. Dengi and L. R. Carley, “Automatic Synthesis of A 2.1 GHz SiGe Low Noise Amplifier,” Proceedings of IEEE Rado Frequency Integrated Circuits Symposium, Seattle, 2-4 June 2002, pp. 125-128.
- M. Chu and D. J. Allstot, “An Elitist Distributed Particle Swarm Algorithm for RF IC Optimization,” Proceedings of Asia South Pacific Design Automation Conference, Shanghai, 18-21 January 2005, pp. 671-674.
- P. Vancorenland, C. De Ranter, M. Steyaert and G. Gielen, “Optimal RF Design Using Smart Evolutionary Algorithms,” Proceedings of Design Automation Conference, Los Angeles, 4-8 June 2000, pp. 7-10.
- G. Tulunay and S. Balkır, “A Compact Optimization Methodology for Single-Ended LNA,” Proceedings of IEEE International Symposium Circuits and Systems, Geneva, 23-26 May 2004, pp. 273-276.
- T.-K. Nguyen, C.-H. Kim, G.-J. Ihm, M.-S. Yang and S.-G. Lee, “CMOS Low-Noise Amplifier Design Optimization Techniques,” IEEE Transactions on Microwave Theory and Technique, Vol. 52, No. 5, 2004, pp. 1433- 1442. doi:10.1109/TMTT.2004.827014
- G. Tulunay and S. Balkir, “Automatic Synthesis of CMOS RF Front-Ends,” Proceedings of IEEE International Symposium Circuits and Systems, Island of Kos, 21-24 May 2006, pp. 625-628.
- A. Nieuwoudt, T. Ragheb and Y. Massoud, “SOC-NLNA: Synthesis and Optimization for Fully Integrated Narrow-Band CMOS Low Noise Amplifiers,” Proceedings of Design Automation Conference, San Francisco, 24-28 July 2006, pp. 879-884.
- W. Cheng, A. J. Annema and B. Nauta, “A Multi-Step P-Cell for LNA Design Automation,” Proceedings of IEEE International Symposium Circuits and Systems, Seattle, 18-21 May 2008, pp. 2550-2553.
- J. Y. Choi, “An Aanalytical Approach for Fast Automatic Sizing of Narrow-Band RF CMOS LNAs,” Circuits and Systems, Vol. 3, No. 2, 2012, pp. 136-145. doi:10.4236/cs.2012.32018
- T. H. Lee, “The Design of CMOS Radio-Frequency Integrated Circuits,” 2nd Edition, Cambridge University Press, Cambridge, 2004.
- “BSIM4.5.0 MOSFET Model, User’s Manual,” University of California, Berkeley, 2004.
NOTES
*This work was supported by 2012 Hongik University Research Fund.