ABSTRACT

The practical significance of the established generalized differential formulation of the first law of thermodynamics (formulated for the rotational coordinate system) is evaluated (for the first time and for the mesoscale oceanic eddies) by deriving the general (viscous-compressible-thermal) and partial (incompressible, viscous-thermal) local conditions of the tidal maintenance of the quasi-stationary energy and dissipative turbulent structure of the mesoscale eddy located inside of the individual fluid region $\tau$ of the thermally heterogeneous viscous (compressible and incompressible, respectively) heat-conducting stratified fluid over the two-dimensional bottom topography $h\left(x\right)$ characterized by the horizontal coordinate $x$ along a horizontal axis X. Based on the derived partial (incompressible) local condition (of the tidal maintenance of the quasi-stationary energy and viscous-thermal dissipative turbulent structure of the mesoscale eddy) and using the calculated vertical distributions of the mean viscous dissipation rate per unit mass $\overline{{\epsilon }_{dis,v}}\left(z\right)$ and the mean thermal dissipation rate per unit mass $\overline{{\epsilon }_{dis,t}}\left(z\right)$ in four regions near the observed mesoscale (periodically topographically trapped by nearly two-dimensional bottom topography) eddy located near the northern region of the Yamato Rise in the Japan Sea, the combined analysis of the energy structure of the eddy and the viscous-thermal dissipative structure of turbulence is presented. The convincing evidence is presented of the tidal mechanism of maintenance of the eddy energy and viscous-thermal dissipative structure of turbulence (produced by the breaking internal gravity waves generated by the eddy) in three regions near the Yamato Rise subjected to the observed mesoscale eddy near the northern region of the Yamato Rise of the Japan Sea.

Keywords:

Generalized Formulation of the First Law of Thermodynamics, Cosmic Gravitation, Small-scale Dissipative Turbulence, Viscous and Thermal Dissipation Rates, Mesoscale Oceanic Eddies, Internal Tide

1. Introduction

It is well known that the problem of turbulence is “the last great unsolved problem of classical physics” [1] , the solution of which has the practical significance for humankind. Based on the assumption of the local thermodynamic equilibrium [2] , De Groot and Mazur [3] , and Gyarmati [4] defined the macroscopic kinetic energy per unit mass ${\epsilon }_k$ as the sum of the macroscopic translational kinetic energy per unit mass ${\epsilon }_t$ and the macroscopic internal rotational kinetic energy per unit mass ${\epsilon }_r$ . We derived [5] the formula for the macroscopic kinetic energy per unit mass ${\epsilon }_k$ generalizing the classical expression ${\epsilon }_k={\epsilon }_t+{\epsilon }_r$ [3] [4] by taking into account the shear component of the macroscopic continuum motion related with the rate of strain tensor $e_{ij}$ [1] [5] . The macroscopic kinetic energy per unit mass ${\epsilon }_k$ is presented [5] as the sum of the macroscopic translational kinetic energy per unit mass ${\epsilon }_t$ [3] [4] [5] [6] and three Galilean invariants: the classical macroscopic internal rotational kinetic energy per unit mass ${\epsilon }_r$ [3] [4] , the established [5] macroscopic non-equilibrium internal shear kinetic energy per unit mass ${\epsilon }_s$ and the established [5] macroscopic non-equilibrium internal kinetic energy of a shear-rotational coupling per unit mass ${\epsilon }_{s,r}^{coup}$ with a small correction ${\epsilon }_{res}$ . The generalized formula [5] for the macroscopic kinetic energy per unit mass ${\epsilon }_k$ was the basis of the non-equilibrium statistical thermohydrodynamic theory [5] [7] [8] [9] [10] [11] of the three-dimensional isotropic homogeneous small-scale dissipative turbulence. The physical correctness of the non-equilibrium statistical thermohydrodynamic theory was demonstrated [5] [7] - [13] for laboratory and oceanic three-dimensional isotropic homogeneous small-scale dissipative stratified turbulence in the wide range of the energy-containing length scales from the inner Kolmogorov length scale [14] to the length scales proportional to the Ozmidov length scale [5] .

The classical Gibbs’ differential formulation [2] [15] of the first law of thermodynamics was generalized [7] [8] [9] [16] - [21] (for the small [7] and for the finite continuum regions $\tau$ considered in the Galilean frame of reference) by taking into account (along with the classical [2] [3] [4] [15] infinitesimal change of heat $\delta Q$ and the classical [2] [3] [4] [15] infinitesimal change $\text{d}{U}_{\tau }\equiv \text{d}U$

of the internal thermal energy $U_{\tau }$ ) the infinitesimal increment $\text{d}{K}_{\tau }$ of the macroscopic kinetic energy $K_{\tau }$ (which contains (for the for the small continuum region $\tau$ [5] [7] ) the classical macroscopic translational kinetic energy [3] [4] , the classical macroscopic internal rotational kinetic energy [3] [4] , the established [5] macroscopic non-equilibrium internal shear kinetic energy and the established [5] macroscopic non-equilibrium internal kinetic energy of a shear-rotational coupling), the infinitesimal increment $\text{d}{\pi }_{\tau }$ of the gravitational potential energy ${\pi }_{\tau }$ , the generalized expression for the infinitesimal work $\delta A_{np,\partial \tau }$ [7] done by the non-potential terrestrial stress forces (characterized by general symmetric stress tensor $T$ [4] ) acting on the boundary surface $\partial \tau$ of the continuum region $\tau$ , the infinitesimal increment $\text{d}G$ (which is not presented in the generalized differential formulation [7] of the first law of thermodynamics for the small continuum region $\tau$ ) of energy due to the combined cosmic and terrestrial non-stationary energy gravitational influence $\text{d}G$ on the continuum region $\tau$ . We founded the generalized thermohydrogravidynamic model [9] [16] [17] [18] of the earthquake focal region based on the generalized differential formulation [9] [16] - [21] of the first law of thermodynamics and using the generalized expression for the infinitesimal work $\delta A_{np,\partial \tau }$ (for the Newtonian continuum [9] [16] [17] [18] [19] [20] ) together with the generalized expression [5] [7] [8] [16] [17] [18] for the instantaneous macroscopic kinetic energy $K_{\tau }$ of the small macroscopic individual continuum region $\tau$ . We founded [9] [21] also the generalized differential formulation of the first law of thermodynamics for the deformed one-component individual finite continuum region $\tau$ (considered in the rotational coordinate system K related with the rotating Earth) subjected to the non-stationary Newtonian terrestrial gravitational field, the tidal, Coriolis and centrifugal forces, and non-potential terrestrial stress forces (characterized by general symmetric stress tensor $T$ [4] ) acting on the boundary surface 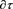of the individual finite continuum region. It was pointed out [21] that the generalized differential formulation of the first law of thermodynamics [9] [16] [17] [18] [19] [20] (for the Galilean frame of reference) is preferable (with respect to the derived generalized differential formulation of the first law of thermodynamics [9] [21] formulated for the rotational coordinate system) for consideration of the regional and global seismotectonic activity of the Earth since it gives the possibility to not consider the variable (in time and space) tidal, Coriolis and centrifugal forces acting on the individual finite continuum region of the Earth. However, in this article we shall consider (for the first time) the established [9] [21] generalized differential formulation of the first law of thermodynamics (formulated for the rotational coordinate system K related with the rotating Earth) for analysis of the energy and dissipative structure of the mesoscale eddy observed [22] in the northwestern part of the Japan Sea near the Yamato Rise. The aim of this article is to bring out the practical significance of the established generalized differential formulation of the first law of thermodynamics [9] [21] (formulated for the rotational coordinate system K related with the rotating Earth) for foundation of the tidal mechanism (related with cosmic non-stationary gravitational field of the Moon) of maintenance of the quasi-stationary energy and dissipative turbulent (not isotropic and not homogeneous) structure of the mesoscale oceanic eddies (especially, located near the Yamato Rise of the Japan Sea [22] ). To do this, in Section 2 we present the equivalent generalized differential formulations (11) and (17) of the first law of thermodynamics [9] [21] for the deformed one-component individual finite continuum region (considered in the rotational coordinate system K related with rotating Earth) subjected to the non-stationary Newtonian terrestrial gravitational field, the tidal forces (related with the cosmic non-stationary gravitational field), the Coriolis and centrifugal forces, and the non-potential terrestrial stress forces acting on the boundary surface 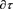of the individual finite continuum region. Based on the established [9] [21] generalized differential formulation (17) of the first law of thermodynamics and the related evolution equation (18) for the total mechanical energy of the deformed finite individual macroscopic region of the Newtonian continuum (considered in the rotating coordinate system), we formulate in Section 3 the general and partial (incompressible) local conditions ((29) and (30), respectively) of the tidal maintenance of the quasi-stationary energy and dissipative (viscous-thermal-compressible and viscous-thermal, respectively) turbulent structures of the mesoscale eddy located inside of the individual fluid region over the two-dimensional bottom topography 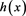characterized by the horizontal coordinate along the horizontal axis X. To evaluate the partial (incompressible) local condition (30) (formulated based on the internal tide generation model [23] and considering the thermally heterogeneous incompressible viscous Newtonian fluid characterized by the classical [6] thermal dissipation rate per unit mass and the classical [3] [4] [5] [6] [7] [14] [24] local viscous dissipation rate per unit mass), in Section 4, we present the calculated vertical

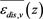distributions of the mean viscous dissipation rate per unit mass characterizing the vertical viscous dissipative structure of turbulence in four regions in the vicinity of the mesoscale eddy. The vertical distributions of are

calculated based on parametrization (45) established using the analysis of the CTD measurements [22] for four regions in the vicinity of mesoscale eddy observed in the northwestern part of the Japan Sea near the Yamato Rise on 25 February-9 March, 2003 in the cruise of R/V Akademik M.A. Lavrentyev. In Section 5, we present the calculated vertical distributions of the mean thermal dissipation rate per unit mass 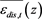characterizing the vertical thermal dissipative structure of turbulence in four regions in the vicinity of the mesoscale eddy. In Section 5, we present also the calculated mean (for all stations in each considered region in the vicinity of the mesoscale eddy) vertical distributions

(of the mean viscous-thermal dissipation rates per unit mass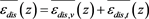) characterizing the vertical viscous-thermal dissipative structure of turbulence in four regions in the vicinity of the mesoscale eddy.

Based on the partial (incompressible) local condition (30), in Section 6, we present the combined analysis of the energy and viscous-thermal dissipative structure of turbulence in the mesoscale (periodically topographically trapped [22] [25] [26] ) eddy located near the northern region of the Yamato Rise in the Japan Sea. In Section 7, we present the summary of main results and conclusion.

2. The Generalized Differential Formulation of the First Law of Thermodynamics for the Rotational Coordinate System Related with the Rotating Earth

Let us consider an individual finite continuum region (characterized by the closed continual boundary surface), which moves in the three-dimensional Euclidean space with respect to rotational Cartesian coordinate system K () related with the rotating Earth (see Figure 1). The rotational Cartesian coordinate system K is centred at the mass center of the rotating Earth and is determined by the axes (see Figure 1) defined by the unit normal coordinate vectors, respectively.

The local hydrodynamic velocity is determined by the general equation of continuum movement (for the rotational coordinate system K) [9] [21] :

(1)

where, is the total acceleration of the physically infinitesimal continuum element, is the total derivative [4] [5] [6] [7] , is an

arbitrary symmetric stress tensor [4] , is the local density of mass distribution, is the local terrestrial gravitational acceleration of the non-stationary gravitational field of the Earth, is the non-stationary terrestrial gravitational potential, is the angular velocity vector of the Earth’s rotation, is the vector characterizing the physically infinitesimal continuum element. According to the general equation (1), the moving rotating deforming heat-conducting stratified one-component individual finite continuum region

is subjected to the terrestrial force, the terrestrial non-stationary Newtonian gravitational field characterized by the local terrestrial gravitational acceleration, the Coriolis force [27] , the centrifugal force [27] and the classical tidal force [28] , which is related predominantly with the non-stationary gravitational field of the Moon and the Sun.

The pressure tensor [4] is given by the decomposition [3] :

(2)

defined by the delta-tensor, the thermodynamic pressure p and the viscous-stress tensor [3] . The differential formulation of the first law of thermodynamics for the one-component deformed continuum element (physically infinitesimal continuum region) with no chemical reactions [3] :

(3)

determines the time evolution of the specific (per unit mass) internal thermal energy u by taking into account the specific volume, the infinitesimal (differential) change of heat (related with the thermal molecular conductivity) across the boundary surface of the continuum element. The infinitesimal change of heat is determined by the classical heat equation [3] :

(4)

which takes into account the density of the heat flux [3] due to the thermal molecular conductivity of heat in the considered continuum.

We use the classical de Groot and Mazur expression [3] for the entropy production (per unit mass) in thermally heterogeneous one-component Newtonian fluid (with no chemical reactions):

(5)

where T is the absolute temperature. The density of the heat flux is determined by the classical Fourier’s law [3] [4] [6]

(6)

where is the coefficient (designated [6] as æ) of thermal molecular conductivity of heat [3] [4] . The relations (5) and (6) give the expression for the total kinetic energy dissipation rate per unit mass (in thermally heterogeneous viscous compressible Newtonian fluid with no chemical reactions):

(7)

where

(8)

is the classical [3] - [8] [14] [24] local viscous dissipation rate per unit mass (in the Newtonian continuum characterized by the local coefficient of molecular kinematic viscosity [5] [6] [7] ) related with the local rate of the strain

tensor [5] [7] ;

(9)

is the classical [3] [4] [6] [7] viscous-compressible dissipation rate per unit mass (in the Newtonian continuum characterized by the coefficient of molecular kinematic viscosity [5] [6] [7] and the coefficient of molecular volume (second) viscosity [5] [6] [7] );

(10)

is the classical [3] [6] thermal dissipation rate per unit mass determined by the coefficient of thermal molecular conductivity of heat, the local absolute temperature T, and the local gradient of the local temperature field.

Based on the general equation (1), the decomposition (2), the differential formulation (3) and the heat equation (4) [3] , we derived [9] [21] the generalized differential formulation of the first law of thermodynamics (for the symmetric stress tensor and for the rotational coordinate system):

(11)

taking into account the classical differential (during the differential time interval) change of heat [2] [4] [15] , the classical differential change of the internal thermal energy [2] [4] [15] , the differential change [9] [21] of the macroscopic kinetic energy:

(12)

the differential change [9] [21] of the gravitational terrestrial potential energy:

(13)

the generalized [9] [21] differential work:

(14)

done by non-potential terrestrial stress forces acting on the boundary surface of the considered individual continuum region, the differential terrestrial energy gravitational influence [9] [21] on the continuum region:

(15)

due to the non-stationary terrestrial Newtonian gravitational field, and the tidal-centrifugal differential work [9] [21] :

(16)

done by the combined tidal and centrifugal forces acting on the considered individual continuum region during the differential time interval.

Based on relations (11), (12), (13), (14), (15) and (16), we obtained [9] [21] the equivalent generalized differential formulation of the first law of thermodynamics (for rotational coordinate system):

(17)

Based on the generalized differential formulation (17) of the first law of thermodynamics, we derived [9] [21] the evolution equation for the total mechanical energy of the finite individual macroscopic region of the viscous compressible Newtonian continuum (fluid):

(18)

which will be used in the next Section 3 for formulation of the general (compressible) and partial (incompressible) local conditions of the tidal maintenance of the quasi-stationary energy and dissipative structure of the mesoscale oceanic eddy located over the two-dimensional bottom topography. Based on the evolution equation (18) and the expression (7) for the total kinetic energy dissipation rate per unit mass (in thermally heterogeneous three-dimensional shear flow of the viscous compressible Newtonian fluid with no chemical reactions), we shall deduce in the next Section 3 the general (compressible) and partial (incompressible) local conditions of the tidal maintenance of the quasi-stationary energy and dissipative structure of the mesoscale eddy located inside of the individual fluid region over the two-dimensional bottom topography. We shall use in the Section 6 the partial (incompressible) local condition (30) for the combined analysis of the energy and viscous-thermal dissipative structure of turbulence in four regions of the periodically topographically trapped [22] [25] [26] eddy in the quasi-stationary state near the northern region of the Yamato Rise in the Japan Sea.

3. The General (Compressible) and Partial (Incompressible) Local Conditions of the Tidal Maintenance of the Quasi-stationary Energy and Dissipative Turbulent Structure of the Mesoscale Eddy Located over the Two-dimensional Bottom Topography

To derive the general (compressible) and partial (incompressible) local conditions of the tidal maintenance of the quasi-stationary energy and dissipative turbulent structure of the mesoscale eddy located inside of the individual fluid region over the two-dimensional bottom topography (characterized by the horizontal coordinate along the horizontal axis X), it is necessary to understand the physical nature of various terms on the right hand side of the evolution Equation (18). The first term describes [9] [21] the total power of the irreversible viscous dissipation (in the Newtonian continuum due to the viscous dissipation rate (in a unit of mass) according to the expression (8)) of the macroscopic kinetic energy inside of the individual region. The second term describes [9] [21] the total power of the irreversible viscous-compressible dissipation (in the Newtonian continuum due to the viscous-compressible dissipation rate (in a unit of mass) related with the compressibility effects (related with the divergence of the local hydrodynamic velocity) according to the expression (9)) of the macroscopic kinetic energy inside of the individual region. The total power of the reversible compressibility effect (related with the influence of the divergence and the thermodynamic

pressure p on the total mechanical energy of the individual

continuum region) is described [9] [21] by the third term. The total powers of the mechanical energy exchange across the boundary surface (between the individual continuum region and its surroundings) are described [9] [21] by the fourth, fifth and sixth terms. The total power of the terrestrial energy gravitational influence (owing to of the non-stationary terrestrial gravitational field) on the individual continuum region is described [9] [21] by the seventh term. The total power of the energy influence (on the individual continuum region) of the centrifugal force is described [9] [21] by the eighth term. The total power of the energy gravitational influence of the tidal force (due to the cosmic non-stationary gravitation) on the individual continuum region is described [9] [21] by the ninth term. Taking into account that the Coriolis force is perpendicular to the hydrodynamic velocity, the total power of the energy influence of the Coriolis force is vanished [9] [21] . The classical [6] thermal dissipation rate per unit mass (given by the relation (10)) is not presented in the evolution equation (18) since the thermal dissipation rate per unit mass characterizes the intermediate dissipation of the macroscopic kinetic energy (owing to the creation of the local heterogeneities of the temperature field), which is converted eventually into the internal heat owing to the viscous dissipation rate per unit mass (given by the relation (8)) and the viscous-compressible dissipation rate per unit mass (given by the relation (9)). To deduce the general (compressible) and partial (incompressible) local conditions of the tidal maintenance of the quasi-stationary energy and dissipative turbulent structure of the mesoscale eddy over the two-dimensional bottom topography, we take into account in the following analysis the first, second and ninth terms on the right hand side of the evolution Equation (18) by disregarding the total powers of the mechanical energy exchange across the boundary surface (between the individual continuum region and its surroundings) due to the compressibility, pressure and viscous effects (related with the third, fourth, fifth and sixth terms), by disregarding the total power of the terrestrial energy gravitational influence on the individual continuum region (related with the seventh term) owing to the time variations of the non-stationary gravitational potential of the Earth, and by disregarding the total power (related with the eighth term) of the energy influence (on the individual continuum region) of the centrifugal force. We make these simplified assumptions to found convincingly the predominant tidal mechanism (related mainly with the ninth term of the evolution Equation (18)) of maintenance of the quasi-stationary energy and viscous-thermal dissipative turbulent structure of the mesoscale oceanic eddies (especially, located near the Yamato Rise of the Japan Sea [22] ).

Let us consider the ninth term on the right hand side of the evolution Equation (18). According to the internal tide generation models [23] for the two-dimensional bottom topography, the tidal force is considered as the sum

(19)

where is the force generating the barotropic (surface) tide, is the force generating the baroclinic (internal) tide related with the generation of internal tidal waves by the interaction of the barotropic tide with the bottom topography. Taking into account the decomposition (19), the ninth term on the right hand side of the evolution equation (18) represents the total mechanical energy production per unit time (in the individual macroscopic region) related with the energy power of the tidal force:

(20)

where

(21)

is the total barotropic kinetic energy production per unit time (in the individual macroscopic region) related with the barotropic tidal force,

(22)

is the total baroclinic mechanical energy production per unit time (in the individual macroscopic region) related with the baroclinic tidal force. According to the statistical analysis of the temperature variations (based on the empirical orthogonal functions [29] ) at different depths throughout the water column near the shelf boundary of the Japan Sea, the baroclinic (internal) tide of the semidiurnal time period is the predominant component of the internal tide in the Japan Sea.

According to the internal tide generation models [23] describing the generation of the internal semidiurnal tide by the barotropic tide over the two-dimensional bottom topography (determined by the bottom depth as a function of the horizontal coordinate along a horizontal axis X), the total barotropic kinetic energy production per unit time (21) is related with the barotropic tide characterized by the following barotropic velocities (along the horizontal axis X and the vertical axis Z, respectively):

(23)

where is the horizontal barotropic velocity component along the horizontal axis X, is the vertical barotropic velocity component along the vertical axis Z, i is the imaginary unity, t is the time, is the circular frequency of the barotropic semidiurnal tide related with the semidiurnal time period, is the maximal horizontal barotropic velocity of the barotropic flow along the horizontal axis X. Owing to the absence of the vertical velocity shear and the vanished divergence ( [23] ) of the barotropic velocity field (given by the components (23) [23] ), the barotropic tide (inside of an abitrary individual region of the Newtonian continuum) is characterized by the vanished (equal to zero) total rate of the viscous dissipation, the vanished total rate of the viscous-compressible dissipation and the vanished total rate of the thermal dissipation of the macroscopic kinetic energy (owing to the constant density of the barotropic tide [23] ). Consequently, the total rates of the viscous dissipation, the viscous-compressible dissipation of the macroscopic kinetic energy, and the thermal dissipation of the macroscopic mechanical energy are related mainly with the baroclinic (internal) tide [23] .

According to the internal tide generation models [23] , the baroclinic tidal force (generating the internal tide) is characterized by the following single vertical real component:

(24)

where the stability frequency is defined by the relation [23] [30]

(25)

depending on the local gravity acceleration g, the distribution of the averaged potential density [30] as a function of the vertical depth z. The total baroclinic mechanical energy production per unit time (given by the relation (22)) is directed to the baroclinic tide due to the interaction of the barotropic (surface) tide with the bottom topography. Based on the decomposition [23] :

(26)

of the total semidiurnal velocity field as the sum of the barotropic () and baroclinic () components, and using the condition, we evaluate the local baroclinic mechanical energy production per unit mass (determining by the relation (22)):

(27)

directed to the unit mass of sea water due to the interaction of the barotropic (surface) tide with the two-dimensional bottom topography. The expression (27) for leads to the vertical distribution (for each horizontal coordinate) of the normalized local baroclinic mechanical energy production per unit mass:

(28)

depending on the vertical depth (coordinate) z.

To found the general (compressible) and partial (incompressible) local conditions of the tidal maintenance of the quasi-stationary energy and dissipative turbulent structure of the mesoscale eddy over the two-dimensional bottom topography, we shall use the first, second and ninth terms on the right hand side of the evolution equation (18), the related relation (27) (for the local baroclinic mechanical energy production per unit mass in the relation (22) for the total baroclinic mechanical energy production per unit time in the individual macroscopic region) and the thermal dissipation rate per unit mass given by the relation (10). Assuming the predominance of the first, second and ninth terms on the right hand side of the evolution equation (18), and using the expression (7) for the total kinetic energy dissipation rate per unit mass, we formulate the following general (compressible) local condition of the tidal maintenance of the quasi-stationary energy and viscous-thermal-compressible dissipative turbulent structure of the mesoscale eddy located inside of the individual fluid region over the two-dimensional bottom topography:

(29)

Taking into account and, and disregarding (in accordance with the classical approach of the incompressible oceanic turbulence [5] [7] [14] [24] [30] ), we obtain from the general local condition (29) the partial (incompressible) local condition (which will be under our analysis in Section 6):

(30)

of the tidal maintenance of the quasi-stationary energy and viscous-thermal dissipative turbulent structure of the mesoscale eddy located inside of the individual fluid region over the two-dimensional bottom topography. In the next Section 4 we shall present the calculated vertical distributions of the mean viscous dissipation rate per unit mass (for consideration of the partial local condition (30)) characterizing the vertical viscous dissipative structure of turbulence in four regions in the vicinity of the mesoscale anticyclonic eddy [22] located just to the north of Yamato Rise in the Japan Sea.

4. Spatial Spectra of Temperature Fluctuations and the Viscous Dissipative Structure of Turbulence in Four Regions near the Mesoscale Eddy

Mesoscale eddies of the Japan Sea are significant factor of oceanic structure and dynamics [31] related with the development of the submesoscale motion, which maintains the strong turbulent mixing [22] . The experimental studies [22] [31] suggested that the turbulent mixing in the eddies core and the subsequent transport of trapped waters is the significant mechanism of formation of the large-scale structure of the Japan Sea intermediate waters. Taking into account a large number of the eddies and their long life-time, we pointed out [22] the significance of eddies for the vertical transport of heat, salt, dissolved oxygen and the biogenic elements in the deep layers the Japan Sea.

The coexistence of internal gravity waves with mesoscale eddies was revealed [32] based on satellite synthetic aperture radar (SAR) images in the sea south of the Grand Banks. It was shown (based on the linear theoretical analysis [33] ) that the shear instability (related with the variability of the eddy current field) is the dynamical mechanism of internal gravity wave generation.

It was shown (based on the revised estimates [34] of net energy transfers between the internal gravity wave and the mesoscale eddy fields) that the wave-eddy coupling is a significant regional source of internal gravity waves. It was confirmed [35] that the dominant source of energy for the internal wave field in the Gulf Stream area is related with the dissipation of mesoscale eddies due to the generation of internal gravity waves during the mesoscale eddy-internal wave interaction.

The prevalent mechanism of the turbulence generation in the oceanic thermocline was associated [30] previously with the breaking internal gravity waves due to the shear instability. We have the proportionality (of the Richardson number Ri and the stability frequency N) (in classical consideration [36] of turbulence generation due to the unstable breaking internal gravity waves), which gives the minimal Ri in the oceanic thermocline in accordance with the proportionality [36] for the turbulent kinetic energy production rate. Consequently, the mean viscous dissipation rate per unit mass should be also proportional to, i.e. explaining the remarkable coexistence of strong stratification and extremely large viscous dissipation of the turbulent kinetic energy in the breaking internal gravity waves. The classical dependence (defined by the spatial wave number k) of the spatial spectra of temperature fluctuations was suggested previously [37] for the internal gravity waves in the presence of fine structure of the temperature field.

To study the fine structure of the temperature field related with an anticyclonic eddy, the CTD survey of northwestern part of the Japan Sea was carried out on 25 February-9 March, 2003 in the cruise of R/V Akademik M.A. Lavrentyev [22] . Special observations were done crossing an anticyclonic eddy of around 70 km in diameter located just to the north of Yamato Rise (see Figure 2(a) and Figure 2(b)). Numbers of some stations (St.) referred in the analysis are indicated on Figure 2(a) and Figure 2(b).

To analyze the calculated [38] spatial spectra of the temperature fluctuations we have divided the survey area into four regions: 1) the eddy core (St. 33, 34, 39 and 40); 2) the edge of the eddy (St. 32, 35, 38 and 41); 3) the region of the frontal zone in the south (St. 17, 36 and 37); and 4) the region of the subarctic waters in the north (St. 30, 31, 42, 43 and 44).

The calculated [38] spatial spectra of the temperature fluctuations are well approximated (for four regions and for all stations characterized by different integer numbers i) by the suggested [37] dependences (indicated by the black approximating lines on Figures 3(a)-(d))

(31)

for the internal gravity waves (characterized by the small spatial wave numbers k) and for the active overturning turbulence (for large k).

We see on Figure 3(a) that the core of the eddy is characterized by the practically identical spatial spectra for stations 33, 34, 39 and 40. Consequently,

we can assume that the mesoscale anticyclonic eddy (located just to the north of Yamato Rise, see Figure 2(a) and Figure 2(b)) generates the breaking internal gravity waves, which produce the intense small-scale dissipative turbulence and related strong turbulent mixing [22] in the mesoscale eddy characterized by the fine microstructure of the temperature field characterized by the suggested [37] dependences (31) for the calculated [38] spatial spectra of the temperature fluctuations in the four considered regions.

It was evaluated [39] that the viscous dissipation rate (per unit mass) (related with the breaking internal gravity waves of the background internal gravity wave field) is distributed proportionally to (i.e.,) throughout the water column. The experimental study [40]

reveals also the similar remarkable coexistence of strong stratification, extremely large turbulent kinetic energy and extremely large viscous dissipation rate of the turbulent kinetic energy at a very sharp front between two eddies in the Kuroshio-Oyashio confluence zone. The authors [40] argued that this remarkable coexistence “is likely an extreme example of a process that occurs much more widely in the ocean, potentially playing an important role in its dynamics and energetics”. Using the calculated [38] spatial spectra (approximating by the suggested [37] dependences (31)) of the temperature fluctuations, we present below the method for calculation of the vertical distributions of the viscous dissipation rate per unit mass for different stations located in the four considered regions.

Based on the Kolmogorov’s refined hypothesis [24] , we founded [10] that the energy spatial spectrum (of the oceanic turbulence) has the general form (characterized by the universal function [10] [30] ):

(32)

where is the kinematic viscosity, is the inner Kolmogorov scale [14] , is the mean viscous dissipation rate per unit mass. Considering the power-law dependences characterized by the power, we obtained [10] from relation (32) the power-law expression for the energy spatial spectrum

. (33)

The power is related with the three-dimensional isotropic homogeneous non-dissipative turbulence of the inertial subrange characterized by the classical [30] Kolmogorov energy spatial spectrum

(34)

for very high (large) turbulent Reynolds numbers. The power is related with the weak anisotropic dissipative turbulence at the final viscous stage of decay [7] [10] . The power is related with the strong (active, overturning) three-dimensional isotropic homogeneous small-scale dissipative turbulence characterized by the energy spatial spectrum [7] [10]

(35)

The power is related with the anisotropic dissipative turbulence characterized by moderate energetics, which is slightly upper than the energetics of the final viscous stage of decay [7] [10] . It was correctly pointed out [41] (based on the numerical evidence) that the energy spatial spectrum is not theoretically consistent with the assumption of weak isotropic turbulence.

The energy spatial spectrum (33) corresponds to the spatial spectrum of the turbulent temperature fluctuations (is the specific heat at the constant pressure) [10] :

(36)

characterized by the same power-law dependence on the spatial wavenumbers k. Using the obtained (as it is evident from Figures 3(a)-(d)) experimental power in the spatial spectrum (36), we have the theoretical power in the energy spatial spectrum (33) in accordance with the revealed [42] [43] energy spatial spectra (in the surface layers of the California current system) based on the high-resolution numerical simulation of the mesoscale eddy turbulence related with transition from mesoscale to submesoscale fluid motion.

Using the obtained experimental power in the energy spatial spectrum (33), we obtain the coefficient in the energy spatial spectrum

(37)

by substituting the relation (37) into the classical condition [30]

, (38)

where [14] is the minimal size [7] [30] of the smallest turbulent eddies. Using the condition [30] [44]

(39)

for the interaction time of turbulence and the stability frequency N, we obtain the maximal energy-containing scale and the turbulent kinetic energy per unit mass

, (40)

(41)

of the anisotropic dissipative turbulence characterized by the power in the spectra (33) and (36), respectively. Substituting relations (40) and (41) into the refined (by the empirical coefficient corresponding to the power in spectra (33) and (36)) Kolmogorov relation [45]

(42)

for the coefficient of turbulent (eddy) viscosity, we obtain the relation

(43)

where is the critical kinetic energy viscous dissipation rate per unit mass [5] [7] [10] , which characterizes the transition from a chaotic overturning turbulent regime to a wave hydrodynamic regime in an incompressible stratified viscous Newtonian fluid. We obtained [38] the numerical coefficient based on the minimal empirical value [46] for oceanic turbulence. Substituting the relation (40) into the following refined [45] semi-empirical relation (refined [45] by introducing the empirical coefficient [45] and by using the coefficient [45] instead of the coefficient [47] , i.e. under condition):

(44)

and equating the relation (44) with the obtained relation (43), we obtained [38] the expression for the mean viscous dissipation rate per unit mass:

(45)

used for the calculation of for all stations in the four considered regions (see Figure 4).

The numerical coefficient is calculated based on the relation [45]

(46)

and under condition [38] related with the experimental value [45] and the Kolmogorov constant [48] . The relation (45) contains the dimensional coefficient, which is consistent with the non-equilibrium statistical thermohydrodynamic theory of the small-scale dissipative turbulence [5] [7] [9] [10] . The dimensional coefficient in relation (45) is in agreement also with the previous evaluation [39] of the viscous dissipation rate (per unit mass) related with the breaking internal gravity waves of the background internal gravity wave field.

The founded parameters, [38] and Ko = 5/3 [48] were used for the calculations of the vertical distributions of the viscous dissipation rate per unit mass shown on Figure 4. The revealed very small variance (for stations 33, 34, 39 and 40) of relatively large maximal values of (on Figure 4(a)) confirms the established intense turbulent mixing [22] in the core of the eddies. It is evident from the Figures 4(a)-(c) that the maximal values of for the core of the eddy, the frontal zone and the edge of the eddy, respectively, are larger than the values of the viscous dissipation rate per unit mass (characterized by the range) observed [49] in the eddies off Kuril Islands. It confirms the strong dissipative dynamics and energetics of the considered mesoscale eddy (shown on Figure 2) in the northwestern Japan Sea. The revealed maximal values of the viscous dissipation rate per unit mass and the maximal variance of at the edge of the considered eddy (see Figure 4(b)) and in the frontal zone (see Figure 4(c)) confirm the established [22] significance of the submesoscale motion related

with the breaking internal gravity waves [31] [37] [39] generating the anisotropic intermittent (locally strong) dissipative turbulence [38] of the frontal zone (shown on Figure 2(a)) and the edge region of the observed mesoscale eddy.

5. The Thermal and Viscous-thermal Dissipative Structures of Turbulence in Four Regions near the Mesoscale Eddy

The vertical distributions of the mean thermal dissipation rate per unit mass (determined by the mean value of the quadratic function of the gradient of the absolute temperature T of the sea water) are calculated based on the following relation:

(47)

for various vertical subranges (characterized by different integer numbers j) of the same vertical length d=204.8 m containing of 4096 numerical values of the vertical gradient with the step equal to 0.05 m. Figure 5 shows the calculated vertical distributions of the mean thermal dissipation rate per unit mass for all stations located in the eddy core (Figure 5(a)), at the edge of the eddy (Figure 5(b)), in the frontal zone (Figure 5(c)) and in the subarctic waters (Figure 5(d)). The calculated averaged vertical distributions (obtained as the average of the all mean thermal dissipation rates per unit mass for each region) are shown by black colour in the eddy core (Figure 5(a)), at the edge of the eddy (Figure 5(b)), in the

frontal zone (Figure 5(c)) and in the subarctic waters (Figure 5(d)). The numerical calculations (shown on Figure 5) demonstrate the increased mean thermal dissipation rate per unit mass in the upper highly turbulent layers (in the eddy core (Figure 5(a)), at the edge of the eddy (Figure 5(b)) and in the frontal zone (Figure 5(c)), and near the range 1500 ¸ 2500 m of depths (in the eddy core (Figure 5(a)), at the edge of the eddy (Figure 5(b)), in the frontal zone (Figure 5(c)) and in the subarctic waters (Figure 5(d))).

We calculate the averaged (based on the all stations in the considered regions (a), (b), (c) and (d)) vertical distributions (of the mean viscous-thermal dissipation rate per unit mass characterizing the vertical viscous-thermal dissipative structure of turbulence in four regions) based on the formula:

(48)

where the averaged (based on the all stations in the considered regions (a), (b), (c) and (d)) vertical distributions (of the mean viscous dissipation rate per unit mass) are shown on Figures 4(a)-(d) by black colour; the averaged (based on the all stations in the considered regions (a), (b), (c) and (d)) vertical distributions (of the mean thermal dissipation rate per unit mass) are shown on Figures 5(a)-(d) by black colour also.

The calculated averaged vertical interpolated distributions of the mean viscous-thermal dissipation rates per unit mass (defined by the relation (48)) are shown on Figures 6(a)-(d), respectively, for the eddy core (Figure 6(a)), the edge of the eddy (Figure 6(b)), the frontal zone (Figure 6(c)) and the subarctic waters (Figure 6(d)).

6. The Combined Analysis of the Energy and Viscous-Thermal Dissipative Structure of Turbulence in Four Regions near the Mesoscale Eddy

The partial (incompressible) local condition (30) gives the partial local normalized condition (for the calculated distributions of and shown on Figure 4 and Figure 5, respectively, for all considered stations in four analyzed regions (see Figure 2(a))

(49)

between the normalized (on the maximal value) local mean viscous-thermal

dissipation rate per unit mass and the normalized local (for arbitrary depth z) baroclinic mechanical energy production per unit mass defined by the relation (28).

The proportionality (49) leads to the corresponding proportionality (for the mean distributions obtained by averaging of the several distributions corresponding to the different stations in each considered region):

(50)

between the normalized averaged (for several stations in each considered region) local mean viscous-thermal dissipation rate per unit mass and the normalized averaged (for the same several stations in each considered region) local baroclinic mechanical energy production per unit mass. Figure

7(a) and Figure 7(d) (especially) demonstrate the satisfactory proportionality

(50) for the eddy core (Figure 7(a)) and for the subarctic waters (Figure 7(d)). However, we can see the significant difference between and in the range of depth 500 ÷ 1400 m of the eddy core (Figure 7(a)).

We see the satisfactory numerical fulfilment (shown on Figure 7(d)) of the derived non-dimensional partial local condition (50) (derived from the partial

incompressible local condition (30)) for the distributions and obtained by averaging of the several distributions corresponding to

the all stations (stations 30, 31, 42, 43 and 44) of the subarctic waters. We see for the Figure 7(d) (corresponding to the subarctic waters, which are not subjected to the influence of the observed eddy) the more remarkable correspondence (for the range of depth 300 ÷ 2700 m) of the calculated normalized averaged (for

several stations of the subarctic waters (d)) local mean viscous-thermal dissipation rate per unit mass and the normalized averaged (for several stations) local baroclinic mechanical energy production per unit mass. The obtained remarkable correspondence (between and) on Figure 7(d)) is the evidence of the validity of the partial

(incompressible) local condition (30) of the quasi-stationary energy and viscous-thermal dissipative structure of the semidiurnal baroclinic tidal motion of the viscous incompressible heat-conducting stratified vortical viscous fluid (over the two-dimensional bottom topography) in the subarctic waters of the Japan Sea.

We use only St. 35 at the edge of the eddy (Figure 7(b)) and St. 36 in the frontal zone (Figure 7(c)) since the different stations from the edge of the eddy and the frontal zone (see Figure 2(a)) have the very large variance of the depth of the sea bottom. The calculated normalized local baroclinic mechanical energies production per unit mass are approximately two times larger (for depths larger than 400 m) than the calculated normalized local mean viscous-thermal dissipation rates per unit mass for St. 35 at the edge of the eddy (Figure 7(b)) and for St. 36 in the frontal zone (Figure 7(c)). A significant predominance (approximately in two times) of the calculated normalized local baroclinic mechanical energy production per unit mass (defined by relation (28)) with respect to the calculated normalized local mean viscous-thermal dissipation rate per unit mass for two considered stations (St. 35 at the edge of the eddy and St. 36 in the frontal zone) suggests a possible influence of the viscous-compressible dissipation rate per unit mass [3] [4] [6] [7] [18] [19] [20] [21] [50] disregarded in the present analysis in the partial (incompressible) local condition (30).

The experimental results (of the acoustic tomography of the large-scale heterogeneities in the ocean [51] ) revealed the significant energy losses related with the propagation of the acoustic signal through the anticyclonic oceanic eddy. According to the first point of view, the revealed significant difference between and at the edge of the eddy (Figure 7(b)) and in the frontal zone (Figure 7(c)) can be related with the significant (but disregarded in our analysis in accordance with the classical approach of the oceanic incompressible turbulence [5] [7] [14] [30] ) viscous-compressible dissipation rate per unit mass (given by the relation (9)) at the edge of the eddy and in the frontal zone (see Figure 2(a)).

According to the second (more adequate) point of view (taking into account a possible influence of the viscous-compressible dissipation rate per unit mass [3] [4] [6] [7] [18] [19] [20] [21] [50] ), but taking into account the predominance of the local viscous dissipation rate per unit mass [3] [4] [5] [6] [7] [14] and the local thermal dissipation rate per unit mass [3] [6] with respect to the disregarded local viscous-compressible dissipation rate per unit mass [3] [4] [6] [7] [18] [19] [20] [21] [50] (in accordance with the classical approach of the oceanic incompressible turbulence [5] [7] [14] [30] ), we see (looking on the Figures 7(a)-(c)) that the partial (incompressible) local condition (30) (and its consequences (49) used for the edge of the eddy (Figure 7(b)) and for the frontal zone (Figure 7(c)), and (50) used for the eddy core (Figure 7(a))) give the convincing evidence of the existence of the significant portion of the local baroclinic mechanical energy production per unit mass (given by the relation (27) and directed to the unit mass of sea water due to the interaction of the barotropic tide with the two-dimensional bottom topography), which is converted to the mechanical energy of the eddy structure, the generation of the internal gravity waves [35] and the established energy of the internal gravity wave-eddy coupling [34] .

The existence of the internal gravity waves is confirmed (based on our statistical analysis of the temperature fluctuations given in Section 4) by the computed spatial spectra (shown on Figure 3) of the temperature fluctuations, which are in good agreement with the suggested [37] dependences of the spatial spectra (on the spatial wavenumber k) under existence of the fine temperature structure produced by the breaking internal gravity waves. Really, looking on the Figures 7(a)-(c), we see that the powers of the transmitted energies to the unit of mass (as a consequence of the semidiurnal baroclinic tidal motion related with semidiurnal baroclinic internal tide [23] of the Japan Sea [29] ) are approximately two times larger (in the range of depth 500 ÷ 1400 m of the eddy core for Figure 7(a), below the depth of near 300 m at the edge of the eddy for Figure 7(b), and below the depth of near 500 m in the frontal zone for Figure 7(c)) than the corresponding viscous-thermal dissipation rates (the normalized averaged local mean viscous-thermal dissipation rate per unit mass for Figure 7(a), and the normalized local mean viscous-thermal dissipation rate per unit mass for Figure 7(b) and Figure 7(c)). It means that the sufficient energy powers are available to transform from the semidiurnal baroclinic internal tide [29] to the mechanical energy of the eddy structure [22] , the generation of internal gravity waves [35] and the established energy of the internal gravity wave-eddy coupling [34] .

Thus, the calculated dependences (which have the more distinct differences between the calculated distributions in the range of depth 500 ÷ 1400 m of the eddy core for Figure 7(a), below the depth of near 300 m at the edge of the eddy for Figure 7(b) and below the depth of near 500 m in the frontal zone for Figure 7(c)) give the obvious evidence (for three regions subjected to the influence of the observed eddy) that the semidiurnal baroclinic internal tide [29] (generated by the semidiurnal barotropic tidal current over the two-dimensional bottom topography [23] ) is the significant energy source of maintenance of the eddy energy and viscous-thermal dissipative structure of turbulence [38] (produced by the breaking internal gravity waves [30] [36] [37] generated by the eddy [22] [32] [34] [35] due to the shear instability [33] ) in three regions (the eddy core (Figure 7(a)), the edge of the eddy (Figure 7(b)) and the frontal zone (Figure 7(c))) near the Yamato Rise subjected to the observed mesoscale eddy.

7. The Summary of Main Results and Conclusion

Based on the evolution equation (18) (deduced from the established [9] [21] generalized differential formulation (17) of the first law of thermodynamics for the rotational coordinate system related with the rotating Earth) for the total mechanical energy of the deformed finite individual macroscopic region of the thermally heterogeneous compressible heat-conducting stratified vortical viscous Newtonian fluid characterized by the classical thermal [3] [6] dissipation rate per unit mass, the classical viscous-compressible [3] [4] [6] [7] [18] [19] [20] [21] [50] dissipation rate per unit mass, and the classical viscous [3] - [8] [14] [24] dissipation rate per unit mass, we have formulated in Section 3 the general (compressible) and partial (incompressible) local conditions ((29) and (30), respectively) of the tidal maintenance (determined by the internal tide [23] ) of the quasi-stationary energy and (viscous-thermal-compressible and viscous-thermal, respectively) dissipative turbulent structure of the mesoscale eddy located inside of the individual fluid region over the two-dimensional bottom topography characterized by the horizontal coordinate along the horizontal axis X. We have formulated the partial (incompressible) local condition (30) (of the tidal maintenance of the quasi-stationary energy and viscous-thermal dissipative structure of the mesoscale eddy) by taking into account the local viscous dissipation rate per unit mass [3] - [8] [14] [24] and the local thermal dissipation rate per unit mass [3] [6] and by disregarding the local viscous-compressible dissipation rate per unit mass [3] [4] [6] [7] [18] [19] [20] [21] [50] in accordance with the classical approach of the oceanic incompressible turbulence [5] [7] [8] [14] [24] [30] [47] .

To use the formulated partial (incompressible) local condition (30), we have presented the analysis of the CTD observations [22] [38] made on 25 February-9 March, 2003 in the cruise of R/V Akademik M. A. Lavrentyev in the northwestern part of the Japan Sea including the area of mesoscale anticyclonic eddy (shown on Figure 2(a) and Figure 2(b)) located near the northern region of the Yamato Rise. We have presented in Section 4 the calculated (based on the analysis of the CTD measurements [22] for four regions in the vicinity of mesoscale eddy) vertical distributions of the mean viscous dissipation rate per unit mass (shown on Figures 4(a)-(d)) characterizing the vertical viscous dissipative structure of turbulence in four regions in the vicinity of the mesoscale eddy observed in the northwestern part of the Japan Sea near the Yamato Rise on 25 February-9 March, 2003 in the cruise of R/V Akademik M.A. Lavrentyev. The vertical distributions of the mean viscous dissipation rate per unit mass are calculated based on parametrization (45) established [38] using the calculated [38] spatial spectra (which are well approximated by the suggested [37] dependences (31) on Figures 3(a)-(d)) of the temperature fluctuations for four regions of the survey area (see Figure 2(a)) and based on the obtained [10] power-law expression (33) (deduced from the founded [10] [30] general form (32) of the energy spatial spectrum of the oceanic turbulence) for the energy spatial spectrum. The eddy core (Figure 4(a)) is characterized by the quasi-homogeneous (in horizontal directions) turbulence related with very small variance (in horizontal directions) of the calculated vertical

distributions of. The revealed maximal values of and the maximal variance of the calculated vertical distributions of at the edge

of the eddy (Figure 4(b)) and in the frontal zone (Figure 4(c)) have confirmed the established [22] existence of the strong submesoscale motion [22] (related with the breaking internal gravity waves [33] [34] [36] [37] ) generating the anisotropic dissipative turbulence (characterized by the powers [41] in the established [10] spectra (33) and (36)) of the frontal zone and the edge region of the considered mesoscale eddy.

Based on the classical [3] [6] relation (10) for the thermal dissipation rate per unit mass (derived from the classical de Groot and Mazur expression (5) [3] for the entropy production per unit mass in thermally heterogeneous one-component Newtonian shear flow with no chemical reactions), we have presented in Section 5 the calculated vertical distributions (shown on Figures 5(a)-(d)) of the mean thermal dissipation rate per unit mass (defined by relation

(47)) characterizing the vertical thermal dissipative structure of turbulence in four regions in the vicinity of the mesoscale eddy, see Figure 2(a).

The calculated vertical distributions of the mean thermal dissipation rate per unit mass are characterized by upper maximums for all stations located in the eddy core (Figure 5(a)), at the edge of the eddy (Figure 5(b)) and in the frontal zone (Figure 5(c)). The calculated vertical distributions of the

mean thermal dissipation rate per unit mass demonstrate the deep

intermediate maximums near the depth of 2000 m for all stations located in the eddy core (Figure 5(a)), at the edge of the eddy (Figure 5(b)), in the frontal zone (Figure 5(c)) and in the subarctic waters (Figure 5(d)). Based on the

obtained vertical distributions of and, we have calculated the

averaged (using the all stations in four considered regions shown on Figure 2(a))

vertical distributions (shown on Figures 6(a)-(d)) of the averaged viscous-thermal dissipation rates per unit mass (defined by the relation

(48)) characterizing the averaged vertical viscous-thermal dissipative structure of turbulence in four regions near the mesoscale eddy (see Figure 2(a)). The

obtained distributions of are characterized by the upper maximums for the eddy core (Figure 6(a)), for the edge of the eddy (Figure 6(b)) and for the frontal zone (Figure 6(c)). The obtained distributions of are

characterized by the deep intermediate maximums near the depth of 2000 m for the eddy core (Figure 6(a)), for the edge of the eddy (Figure 6(b)), for frontal zone (Figure 6(c)) and for the subarctic waters (Figure 6(d)).

Based on the derived partial (incompressible) local condition (30) (of the tidal maintenance of the quasi-stationary energy and viscous-thermal dissipative turbulent structure of the mesoscale eddy located inside of the individual fluid region over the two-dimensional bottom topography characterized by the horizontal coordinate along the horizontal axis X), and using the calculated

vertical distributions of (shown on Figures 4(a)-(d)), (shown on Figures 5(a)-(d)) and (shown on Figure 6(a) and

Figure 6(d)), we have presented in Section 6 the combined analysis of the energy and viscous-thermal dissipative structure of turbulence in four regions near the mesoscale (periodically topographically trapped [22] [25] [26] ) eddy located near the northern region of the Yamato Rise (characterized by the nearly two-dimensional bottom topography) in the Japan Sea. We have shown that the subarctic waters (which are not subjected to the influence of the observed eddy) are characterized by the more remarkable numerical fulfilment (shown on Figure 7(d)) of the non-dimensional partial local condition (50) of the quasi-stationary energy and dissipative structure (derived from the partial incompressible local condition (30)) for the normalized (on the maximal value)

averaged distributions and obtained by normalization

and averaging of the several distributions corresponding to the all stations (Sts. 30, 31, 42, 43 and 44) of the subarctic waters. This remarkable correspondence

(between and) shown on Figure 7(d)) may be considered as the example of the dissipative structures introduced [52] [53] to

emphasize a remarkable association between structure (related in the considered case with the structure of the normalized averaged local baroclinic mechanical energy production per unit mass shown on Figure 7(d) and irreversible dissipation of energy (related in the considered case with the normalized averaged local mean viscous-thermal dissipation rate per unit mass) shown on Figure 7(d).

Taking into account that the calculated normalized local baroclinic mechanical energies production per unit mass (the calculated normalized powers of the transmitted energies to the unit of mass as a consequence of the semidiurnal baroclinic tidal motion related with semidiurnal baroclinic internal tide [23] of the Japan Sea [29] ) are approximately two times larger than the calculated normalized local mean viscous-thermal dissipation rates per unit mass for St. 35 (below the depth of near 300 m) at the edge of the eddy (Figure 7(b)) and for St. 36 (below the depth of near 500 m) in the frontal zone (Figure 7(c)), and taking also taking into account that the normalized averaged (for the stations 33, 34, 39 and 40 in the eddy core) local baroclinic mechanical energy production per unit mass (shown on Figure 7(a)) is approximately two times larger (in the range of depth 500 ÷ 1400 m of the eddy core) than the normalized averaged (for the same stations) local mean

viscous-thermal dissipation rate per unit mass, we conclude (based

on the partial incompressible local condition (30)) that the semidiurnal baroclinic internal tide (generated by the semidiurnal barotropic tidal current over the nearly two-dimensional bottom topography [23] in the Japan Sea [29] near the Yamato Rise) is the significant energy source of maintenance of the eddy energy and viscous-thermal dissipative structure of turbulence (produced by the breaking internal gravity waves [30] [36] [37] generated by the eddies [22] [32] [34] [35] due to the shear instability [33] ) in three regions near the Yamato Rise (the eddy core (Figure 7(a)), the edge of the eddy (Figure 7(b)) and the frontal zone (Figure 7(c))) subjected to the observed mesoscale eddy.

Acknowledgements

Avoid the stilted expression, authors thank reviewers for significant remarks and questions taken into account with gratitude for correction of the article. Authors thank Mrs. A.V. Sereda for help in numerical calculations and Mr. I.A. Kuskov for help in graphic presentation of the calculated results. One of us (S. V. S.) thanks with gratitude Jane GAO, Editorial Assistant of JMP for the best editorial assistance.

Cite this paper

Simonenko, S.V. and Lobanov, V.B. (2018) The Application of the Generalized Differential Formulation of the First Law of Thermodynamics for Evidence of the Tidal Mechanism of Maintenance of the Energy and Viscous-Thermal Dissipative Turbulent Structure of the Mesoscale Oceanic Eddies. Journal of Modern Physics, 9, 357-386. https://doi.org/10.4236/jmp.2018.93026

References