Journal of Modern Physics
Vol.08 No.13(2017), Article ID:81135,8 pages
10.4236/jmp.2017.813131
The Hubble Field vs Dark Energy, Part II: The Lagrange-Hamilton Equation and Some Concepts on Force, Energy and Tensors in the Hubble Field
*retired.
Lartigue G. Juan*
Faculty of Chemistry, National University of México, México City, México

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 4, 2017; Accepted: December 15, 2017; Published: December 18, 2017
ABSTRACT
In a recent article [1] the author of this Part II proposed the parameter ΓH for the acceleration expansion of the Universe, instead of dark energy, defining such parameter as = a constant. A question about the expansive and constant acceleration of the internal levels of the Universe could be solved by equation ((3.10) ref. [1] ) of the same article: Any assumed internal distance, lower than r of (ref. [2] ) implies a proportional change in the squared Hubble parameter, so maintaining the constancy of the ΓH value for every stratum of the Universe. In the present work it is proved the constancy of the Hubble force by means of its generalized coordinates. As well, an equation to relate the Lagrange and the Hamilton functions is obtained for the Hubble field. Two concepts for both Hubble’s energy and tensor are also proposed. Finally, prior misprints of Part I, ref. [1] , are corrected in the Appendix.
Keywords:
Hubble Law, Hubble Force, Generalized Coordinates

1. Introduction
1.1. A Summary of Previously Derived Hubble Concepts in Ref. [1]
a) The Hubble field intensity, , (equation (2.1), ref. [1] ) was deduced as a constant in (Equation (2.12), ref. [1] ). Its numerical value, for the assumed radial distance [2] , is that, together the Universe gravitational field intensity , gives a net expanding acceleration of 0.75 × 10−9 (m/s2) which, at the present Hubble time of 4 × 1017 (s), gives the actual Universe expansion speed v = c.
b) The Hubble field potential is expressed as:
(1.1)
c) In the gravitational case, the Poisson equation is a concept that may be related to the Gauss flux Φ defined [3] as the surface integral of the normal component of the intensity of the gravitational field. If the surface is that of a sphere, the Gauss law may also be expressed as:
(1.2)
rM = the mass density. In the Hubble field case, it was shown in equation (4.3), ref. [1] ) that the solution of the Poisson equation is:
(1.3)
1.2. Objectives of Part II of the Paper
They would be to clarify some of previous concepts and to add several Hubble new ones: the generalized force, the Lagrange-Hamilton equation, concepts on energy and a tensor.
2. The Hubble Force
In the gravitational field, the intensity and the potential are functions of mass. In the Hubble field it was necessary to apply the Hubble intensity and potential to the proper mass to get an idea of their magnitude since, anyway, it is by means of mass that the Hubble phenomena are perceived; i e, the movements of mass in the Universe would serve as well as a detector to determine the magnitude of the Hubble functions.
Since the intensity of the Hubble field is and if it may be applied as the acceleration of the total Universe mass MU, this could be assumed as a factor of proportionality for the present value of Hubble force:
(2.1)
A necessary condition to mix gravitational and Hubble parameters would be that FH should be a constant of movement. To prove that, it will be applied the Poisson brackets criteria: The generalized expression of force is [4] :
(2.2)
The conservation equation, by means of the Poisson brackets, is:
 (2.3)
(2.3)
or
(2.4)
if Hamilton equations:
and ,(2.4 bis), were substituted.
,(2.4 bis), were substituted.
Then, since the Poisson bracket = 0 in Equation (2.4), the function Q may be assumed to be a constant of movement:
(2.5)
Being QH and therefore FH a constant of movement it could be taken, as an example, that with a result FH = 1.65 × 1046 (Newton). Since FH has not been proved to be originated from any known physical entity, this example shows only the possible magnitude of the Hubble force FH.
With regard to the first form of the Lagrange equation, the generalized force Q may be substituted by F, from Equation (2.2), and this one may also be substituted by the negative gradient of the potential energy, , as:
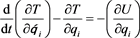 (2.6)
(2.6)
However, in the Hubble case, the force has been defined as the positive gradient of the Hubble potential energy,
(2.7)
Otherwise, the Lagrangian scalar is defined as:
(2.8)
being T and U the kinetic and potential energies. The Hamiltonian is defined as:
(2.9)
Therefore, since U is not a function of the velocity 8i, it is possible to write:
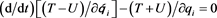 (1.10)
(1.10)
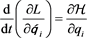 (2.11)
(2.11)
(this would be the Lagrange-Hamilton equation in the Hubble field).
3. The Hubble Energy EH
3.1. The Energy of Vacuum
Gravitational potential is an intrinsic property of mass, i e, mass constitutes the reference frame of the gravitational energy whose potential refers to the unitary mass. The Hubble potential becomes apparent in the presence of astronomical matter, though it does not seem to be generated by any known physical factor. It seems rather to be a quality of the empty space (i.e. the vacuum) defined as the absence of known matter in a determined system. Reference [5] reminds the deduction of the classical thermo-dynamical equation:
(3.1)
In the right side of this equation it is usually omitted the factor c2. The value of α has been analyzed to confirm the possibility for dark energy, if α = −1 [6] .
As well, reference [5] shows that the vacuum energy Ev is proportional to the vacuum volume if the vacuum energy density rv keeps constant:
(3.2)
The same equation could be applied to the Hubble energy EH, as:
(3.3)
or (3.3 bis),
where rH would refer to matter non detectable up to date.
The first theoretical approach to a Universe without matter was that of De Sitter, whose equation of general relativity for an empty Universe [7] required that the energy-momentum tensor would be 0. Besides, he even stated that Equation (3.1) is not realistic unless pressure and density would be, separately, equal to 0. Both conditions were assumed in the De Sitter model though, accordingly to ref. [5] , rv is not necessarily 0.
The above mentioned characteristic of the Hubble energy (to exist without a mass frame) implies the possibility to have existed before the Big Bang.
3.2. Forms of the Hubble Energy
Previous words would mean that the original Hubble energy is a potential one, able to be converted to kinetic energy in the presence of matter. That means that the detection and measurement of the Hubble energy require the presence of mass movements. The value of the present Hubble potential energy UH could be estimated by the product of the Hubble field potential (Equation (2.1)) and the assumed mass MU of the Universe:
(3.4)
it gives a total value for UH = 3.6 × 1072 (J). Though not formally deduced, this figure shows the potential energy that the Hubble field would imply to date.
Since the Hubble field intensity ΓH (m/s2) has the units of an acceleration, it has been directly associated to the Hubble force (equation (2.1)). As well, when ΓH is integrated between 0 and r, it gives a squared velocity divided by 2, which represents the Hubble potential VH. If this one is multiplied by the Universe mass, it gives an equation similar to a Hubble kinetic energy:
(3.5)
Therefore, the total Hubble energy would be:
(3.6)
The density of EHis: (3.6 bis).
Equations ((3.4) and (3.5)) show that the Hubble potential energy and kinetic energy have the same value at a given position r. From those equations and (3.6) it seems to correspond to each one, at position r, 50% of the total Hubble energy. Obviously, all of that cannot really be similar to the gravitational case whose respective potentials have opposite signs. For example, in the gravitational case, the 0 value of the potential energy of a mass M corresponds to R(t) = ∞; the value at an initial position r1 it could be −U1; at a lower position r2 it could be −U2; at the observer’s position (r = 0) it is usually assumed that Uo = −∞; so, in the case of a falling mass from positions 1 to 2, the change in potential energy is:
(3.7)
Simultaneously, the increase in the kinetic energy, DK is equal to the difference in the modules of potential energy: .
Therefore, in the gravitational case, the increase in the kinetic energy of a falling mass comes from the decrease in its potential energy; otherwise, since kinetic energy may be generated by nuclear, chemical or electromagnetic potentials, it may also be, sometimes, converted to potential energy.
In the Hubble case, it will not be possible a falling situation since it exists, exclusively, the expansive one. So, the total Hubble energy given by Equation (3.6) should not be divided in potential and kinetic ones: it is a new form of energy that simultaneously appears as potential and kinetic. However, in Hubble and Newtonian fields, matter remains as the only field monitor.
4. The Hubble Tensor
The acceleration in a coordinate k, ak, is the intrinsic derivative of vk:
, it is a contravariant tensor, rank 1 (a vector). (4.1)
The Newton second law may be expressed for the invariant M as:
(4.2)
In case that the Hubble force would be covariant, its module would be:
(4.3)
since both UH and (Fk)H are positive.
In a previous work [1] it was foresaw the possibility for a tensor (Tμν)Ʌ from an equation given by reference [8] that included the parameter in the Einstein gravitational equation:
(4.4)
The two first terms are known as the Einstein tensor Gμν.
As mentioned above, the De Sitter model assumed that, in an empty Universe, the energy-momentum tensor would be 0; this means that:
(4.5)
The right side of this equation gives a definition of a possible tensor. It would be then necessary to convert the tensor term into a Hubble function, as it will be intended as follows: contraction of the last equation gives the scalar of curvature in the empty space:
(4.6)
From ref. [1] it was shown that
(4.7)
The substitution in Equation (4.6) gives, for the scalar of curvature of the free space:
(4.8)
A definition for the Hubble tensor, similar to that proposed for the tensor, from Equations (4.5) and (4.7) would be:
(4.9)
The scalar of the Hubble tensor is:
(4.10)
Equation (4.9) may be substituted in Equation (4.5) to yet include an additional tensor (as proposed and later cancelled by Einstein) in the gravitational equation, now based on the better known, and measured, Hubble parameter:
(4.11)
The main raison to include now a Hubble expansive term in the gravitational Einstein equation is that he tried to maintain static his equation by means of his cosmological term Ʌ, which was ignored by Friedmann and abandoned by Einstein when the Universe expansion was confirmed by Hubble. Today, since the original energy-momentum tensor was cancelled in the De Sitter model, the added expansive tensor (Tμν)H must now be (given the astronomical observations), in the same order than the Einstein tensor; it should be, therefore:
(4.12)
starting from the critical time.
As it is known, the second term originated under the condition: div Gμν→ 0 at the Newtonian limit. From equation (4.9), divergence of the first term tends to 0 as r → ∞ since its divergence results reciprocal of r.
Otherwise, such as in the case [8] , the Hubble parameter may also be expressed, similarly to equations (2.1), ref. [1] and 4.4, ref. [1] , as a function of the vacuum Hubble energy density:
(4.13)
5. Conclusions
1) Previous results: are presented in this Part II, related to the Hubble acceleration constant ΓH: a correction in the Appendix to equation (3.8, ref. [1] ) about the Hubble potential ; a commentary on the various possible solutions to the Poisson equation that, accordingly to the applied matter, would be: equal to 0 in the absence of matter; proportional to mass density in the case of mass presence; proportional to the second derivatives of the electric and magnetic field intensities (whose sum of squared is proportional to the e.m. field density); and equal to H2 in the Hubble field, equation (4.4, ref. [1] )).
2) The Hubble force: it was analyzed by its generalized equation and it was concluded that QH, as well as FH, are both constants of movement. As well, it was derived a new form of the Lagrange equation including the Hamiltonian in the Hubble field, equation (2.11). Otherwise, it would result that the Lagrangian = 0.
3) Energy: Initially, It was tried to define the Hubble energy in two parts: potential energy UH and kinetic energy KH. Since the last one gave the same equation than the potential energy, it will not be useful to consider the Hubble energy as behaving in identical form to that of gravitational energy: Equation (3.4) would give the value of the Hubble potential energy, which is always growing with distance r. Simultaneously the Hubble kinetic energy (equation (3.5) also grows in the same proportion, so implying that the Hubble energy has a very different nature than the gravitational energy. It is a new form of energy: it is continuously shown evident, and it would exist since the Big Bang epoch or before.
4) The Hubble energy density: it has been obtained an equation (3.6 bis) for the Hubble energy density. Its present value is about 3.5 (erg/m3).
5) The Hubble tensor scalar: (Tμν)H has been defined as a covariant tensor, rank 2, proportional to H2, Equation (4.9). Its scalar (T)H is equal to the magnitude.
6) The Hubble tensor in G.R.: it has been included in the gravitational equation (4.11), as a time function of the Hubble field tension, equation (4.12). As it is known, the divergence of the gravitational term tends to 0 in the Newtonian limit; however, the divergence of the Hubble term tends to 0 as r → ∞.
7) Other ways: obviously, the search for Dark Energy continues by new physical theories and experiments [6] [9] .
Cite this paper
Juan, L.G. (2017) The Hubble Field vs Dark Energy, Part II: The Lagrange-Hamilton Equation and Some Concepts on Force, Energy and Tensors in the Hubble Field. Journal of Modern Physics, 8, 2159-2166. https://doi.org/10.4236/jmp.2017.813131
References
- 1. Lartigue, J. (2016) Journal of Modern Physics, 7, 1607-1615. http://dx.doi.org/10.4236/jmp.2016.712145
- 2. NASA/MAP Science Team (2014) http://map.gsfc/nasa.gov/universe/uni_matter
- 3. Lindsay, R.B. and Margenau, H. (1957) Foundations of Physics. Dover Inc., 284.
- 4. Anderson, J.M. (1967) Mathematics for Quantum Chemistry. W. A. Benjamin, 112.
- 5. Cassé, M. (2001) Du vide et de la création. 3th Edition, Odile Jacob, Paris, 269-270.
- 6. Valkenburg, W., et al. (2013) Physics of the Dark Universe, 2, 219-223. https://doi.org/10.1016/j.dark.2014.01.001
- 7. Tolman, R.C. (1958) Relativity, Thermodynamics and Cosmology. Oxford Clarendon Press, 348.
- 8. Bergstrom, L. and Goobar, A. (2004) Cosmology. Eqs. (4.3, 4.15) Springer.
- 9. US Dark Energy Task Force, Final Report (2006).
Appendix on Erratum in the Article “The Hubble Field vs Dark Energy”
Under the exclusive responsibility of the author, in some discharges of the previous article, ref. [1] , there appear several errors and misprints. Some corrections follow:
a) It lacks the double point on the ä of equations (1.8 and 1.8 bis, [1] ).
b) In the right side of Equation (3.8) it lacks the denominator 2, i.e.:
(3.8, ref. [1] ).
c) The headings of figure 1 and table 1 appear sometimes blocked with a black bar due to the blue color applied in the original paper.

