Journal of Modern Physics
Vol.07 No.08(2016), Article ID:66195,16 pages
10.4236/jmp.2016.78073
Non-Perturbative Analysis of Various Mass Generation by Gluonic Dressing Effect with the Schwinger-Dyson Formalism in QCD
Shotaro Imai1, Hideo Suganuma2
1Institute for the Advancement of Higher Education, Hokkaido University, Sapporo, Japan
2Department of Physics, Graduate School of Science, Kyoto University, Kyoto, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 February 2016; accepted 26 April 2016; published 29 April 2016
ABSTRACT
As a topic of “quantum color dynamics”, we study various mass generation of colored particles and gluonic dressing effect in a non-perturbative manner, using the Schwinger-Dyson (SD) formalism in (scalar) QCD. First, we review dynamical quark-mass generation in QCD in the SD approach as a typical fermion-mass generation via spontaneous chiral-symmetry breaking. Second, using the SD formalism for scalar QCD, we investigate the scalar diquark, a bound-state-like object of two quarks, and its mass generation, which is clearly non-chiral-origin. Here, the scalar diquark is treated as an extended colored scalar field, like a meson in effective hadron models, and its effective size R is introduced as a form factor. As a diagrammatical difference, the SD equation for the scalar diquark has an additional 4-point interaction term, in comparison with the single quark case. The diquark size R is taken to be smaller than a hadron, R ~ 1 fm, and larger than a constituent quark, R ~ 0.3 fm. We find that the compact diquark with R ~ 0.3 fm has a large effective mass of about 900 MeV, and therefore such a compact diquark is not acceptable in effective models for hadrons. We also consider the artificial removal of 3- and 4-point interaction, respectively, to see the role of each term, and find that the 4-point interaction plays the dominant role of the diquark self-energy. From the above two different cases, quarks and diquarks, we guess that the mass generation of colored particles is a general result of non-perturbative gluonic dressing effect.
Keywords:
Dynamical Mass Generation, Diquarks, Schwinger-Dyson Formalism, QCD

1. Introduction
Quantum chromodynamics (QCD) is the fundamental gauge theory of the strong interaction, and it is a long important problem to describe hadron structure and properties based on QCD. Quarks and gluons, the basic ingredients of QCD, strongly interact with each other in an infrared region, and they are confined in hadrons. Then, due to their non-perturbative properties, it is fairly difficult to describe hadrons directly from QCD. Also, the non-perturbative dynamics in QCD directly relates to the other important physical subject of “mass generation.”
The origin of mass is one of the most fundamental issues in physics. One famous category of mass generation is the Yukawa interaction with the Higgs field. However, even besides the dark sector, the Higgs-origin mass is only about 1% of the total mass in our universe, where dominant massive particles are nuclei (u,d quarks) and electrons. Actually, the Higgs interaction only gives the electron mass (about 0.5MeV) and a small current quark mass (a few MeV) for u,d quarks [1] . In contrast, about 99% of mass of matter in our universe are created by the
strong interaction, apart from the dark sector. In fact, a large constituent quark mass of 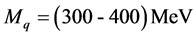 arises from non-perturbative dynamics in QCD. Thus, QCD gives another category of mass generation.
arises from non-perturbative dynamics in QCD. Thus, QCD gives another category of mass generation.
Such a dynamical fermion-mass generation in the strong interaction was first pointed out by Y. Nambu et al. [2] in 1961 in the context of spontaneous chiral-symmetry breaking. The QCD-based quantitative analysis of dynamical fermion mass generation was performed by Higashijima and Miransky in 1980’s [3] [4] using the Schwinger-Dyson formalism. Thus, light u,d-quarks are considered to acquire a large constituent quark mass of about 300 - 400 MeV, in accordance with spontaneous chiral-symmetry breaking.
Even without chiral symmetry breaking, however, it is likely that QCD has several dynamical mass generation mechanism. For example, while the charm quark has no chiral symmetry, some difference seems to
appear between current and constituent masses for charm quarks: the current mass is 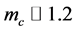 GeV at renor- malization point
GeV at renor- malization point 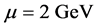 [1] , and the constituent charm quark mass is
[1] , and the constituent charm quark mass is 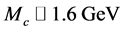 in the quark model.
in the quark model.
The gluon is more drastic case. While the gluon mass is zero in perturbation QCD, the non-perturbative effect of the self-interaction of gluons seems to generate a large effective mass of 0.6 GeV [5] - [7] , and the lowest glueball mass is about 1.6GeV [8] [9] . Furthermore, the dynamical mass generation for scalar-quark have been studied in the lattice scalar-QCD calculation [10] . Thus, we deduce that “quantum color dynamics” generally accompanies a large mass generation, due to the strong interaction.
Next, let us consider compositeness of hadrons in terms of quarks. As an infrared effective theory, the constituent quark model has been successful for the description of the hadron spectroscopy. The constituent
quark belongs to the fundamental representation 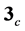 in the
in the 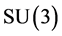 color group, and many hadrons can be
color group, and many hadrons can be
classified as the color-singlet (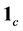 ) bound states of some quarks and antiquarks. In this picture, ordinary mesons and baryons are identified as quark-antiquark and three-quark systems, respectively. However, besides the ordinary baryons and mesons, QCD allows the existence of other color-singlet states, such as glueballs, hybrids and multi-quark states, called exotic hadrons. Recent experiments have reported the candidates for these exotic states [1] . The heavy hadrons, which includes one or more heavy (anti)quarks, are also recent hot topics in hadron physics [1] [11] [12] . For example, very recently, LHCb has reported the discovery of two charmed pentaquarks,
) bound states of some quarks and antiquarks. In this picture, ordinary mesons and baryons are identified as quark-antiquark and three-quark systems, respectively. However, besides the ordinary baryons and mesons, QCD allows the existence of other color-singlet states, such as glueballs, hybrids and multi-quark states, called exotic hadrons. Recent experiments have reported the candidates for these exotic states [1] . The heavy hadrons, which includes one or more heavy (anti)quarks, are also recent hot topics in hadron physics [1] [11] [12] . For example, very recently, LHCb has reported the discovery of two charmed pentaquarks, 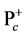 (4380) and
(4380) and 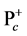 (4450), from a careful analysis of the decay product in the high-energy process, and this report seems to activate the multi-quark physics again [13] .
(4450), from a careful analysis of the decay product in the high-energy process, and this report seems to activate the multi-quark physics again [13] .
In the theoretical study of these states, the diquark picture [14] [15] has been discussed as an important effective degree of freedom. The diquark is composed of two quarks with strong correlation, where the
one-gluon-exchange interaction between two quarks is attractive in the color anti-triplet 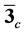 channel [16] [17] , of which color is the same as an anti-quark. In
channel [16] [17] , of which color is the same as an anti-quark. In 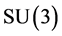 flavor case, the flavor-antisymmetric and spin-singlet
flavor case, the flavor-antisymmetric and spin-singlet
with even parity is the most attractive channel in diquark, which is called scalar diquark. If the diquark correlation is developed in a hadron, this scalar diquark channel would be favored. The diquark correlation in a hadron is discussed in various situations, such as tetra-quarks, heavy baryons and other exotic states [18] [19] . The tetra-quark states as the bound state of the diquark/antidiquark is suggested in early day [20] , and X(3872) [21] and X(1576) [22] are considered as tetra-quark states. Light flavor mesons as tetra-quark [23] - [32] and mixing with 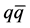 state [33] - [35] are discussed. There are various studies the heavy baryons focused on diquark [36] - [40] , e.g., single heavy quark/light diquark (
state [33] - [35] are discussed. There are various studies the heavy baryons focused on diquark [36] - [40] , e.g., single heavy quark/light diquark (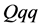 ) picture [41] - [45] . The other exotic states including heavy quark(s) are studied [46] - [52] . The ordinary baryon properties focused on the diquarks have been also discussed [53] - [57] . The diquark correlation is found in the lattice QCD simulation [58] - [61] . It is also considered that the diquark condensation is occurred in an extremely high density system, called the color superconductivity [62] . We note that diquark properties strongly depend on the color number
) picture [41] - [45] . The other exotic states including heavy quark(s) are studied [46] - [52] . The ordinary baryon properties focused on the diquarks have been also discussed [53] - [57] . The diquark correlation is found in the lattice QCD simulation [58] - [61] . It is also considered that the diquark condensation is occurred in an extremely high density system, called the color superconductivity [62] . We note that diquark properties strongly depend on the color number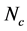 . If we consider the two-color QCD, the diquarks compose the color singlet (baryons). The strength of correlation between two quarks is same as quark/antiquark channel, and the (diquark-)baryons correspond to the mesons. This fact is known as the Pauli-
. If we consider the two-color QCD, the diquarks compose the color singlet (baryons). The strength of correlation between two quarks is same as quark/antiquark channel, and the (diquark-)baryons correspond to the mesons. This fact is known as the Pauli-
Gürsey symmetry. The quark-hadron matter in two-color system is investigated [63] - [69] . For the 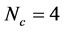 case, the diquarks belong to
case, the diquarks belong to 
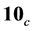


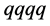



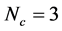
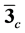
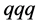

The properties of diquarks such as the mass and size are not understood well, although the diquarks have been discussed as important object of hadron physics. While the diquark is made by two quarks with gluonic interaction, it still strongly interacts with gluons additionally because of its non-zero color charge. Therefore, such dressing effect of gluons for diquark should be considered in a non-perturbative way. The dynamics of diquark and gluons may affect the structure of hadrons. In the quark-hadron physics, the Schwinger-Dyson (SD) formalism is often used to evaluate the non-perturbative effect based on QCD [3] [4] [70] - [78] . In this paper, we apply the SD formalism to scalar diquark to investigate the effective mass of scalar diquark, which reflects a non-perturbative dressing effect by gluons. The scalar diquark is treated as an extended field like a meson in effective hadron models, and interacts with the gluons [10] [42] .
For the argument of the scalar diquark, it would be important to consider its effective size. For, point scalar particles generally have large radiative corrections even in the perturbation theory [79] [80] . As an example, in the framework of the grand unified theory (GUT), the Higgs scalar field suffers from a large radiative correction of the GUT energy scale, and therefore severe “fine-tuning” is inevitably required to realize the low-lying Higgs mass of about 126 GeV [81] , which leads to the notorious hierarchy problem [79] [80] . The Higgs propagator with radiative correction has been investigated by setting the mass renormalization condition to reproduce 126 GeV [82] - [84] . A similar large radiative correction also appears for point-like scalar-quarks, which correspond to compact scalar diquarks, in scalar lattice QCD calculations [10] . In fact, the point-like scalar-quark
interacting with gluons acquires a large extra mass of about 1.5 GeV at the cutoff
lattice spacing. Such a large-mass acquirement would be problematic in describing hadrons with scalar diquarks. However, since it is a bound-state-like object inside a hadron, the diquark must have an effective size. This effect gives a natural UV cutoff of the theory, and reduces the large radiative correction. Then, we take account of the effective size and investigate the mass of the scalar diquark inside a hadron within the SD formalism.
This paper is organized as follows. In Section 2, we review the SD formalism for the light quark, as the typical fermion mass generation in QCD. In Section 3, we investigate the SD equation for the scalar diquark, where a simple form factor is introduced for the possible size of diquark. In Section 4, we present the numerical result of the diquark self-energy with the dependence of the bare mass and size of diquark, and briefly discuss the dynamical mass generation for the scalar diquark in the SD formalism. Section 5 is devoted to conclusion and discussion.
2. Dynamical Mass Generation of Quarks in QCD
The chiral symmetry is a fundamental symmetry in the light-quark sector of QCD, and it is an exact global symmetry in the chiral limit. In the low-energy region of QCD, spontaneous chiral-symmetry breaking takes place, which generates a large effective mass of light quarks. Actually, in the theoretical analysis with the Schwinger-Dyson (SD) formalism in QCD, a large self-energy generation of quarks is demonstrated in an infrared region, which breaks the chiral symmetry in the physically stable vacuum [3] [4] . In this section, as the standard fermionic mass generation in QCD, we briefly review the quark mass generation in the SD formalism for QCD in the Landau gauge, which is frequently used. This review part gives a important basis for the non-perturbative QCD physics, and is also useful to set up the formalism for the scalar diquark case in Section 3.
As a merit of the Lorentz-covariant gauge like the Landau gauge, the dressed quark propagator is generally described as 


expressed in Figure 1. In principle, the quark propagator is exactly obtained by solving this equation, if the exact form of the gluon propagator and the quark-gluon vertex are given. Here, the kernel in the SD equation
depicted in Figure 1 is expressed by the product of the quark-gluon vertex 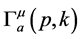


where 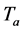

In the most SD studies for quarks, one takes the rainbow-ladder approximation with the renormalization- group improvement of the quark-gluon vertex at the one-loop level. Note that, owing to the iterative structure of the SD equation, a simplified full-order treatment on the coupling 

Here, we briefly mention the treatment of quark confinement in the SD approach. In most works of the SD approach, the confinement effect is ignored, which seems problematic for the study of QCD. On this point, several recent studies, both analytical works [86] and lattice QCD simulations [87] , have suggested that chiral symmetry breaking and quark confinement are not directly correlated in QCD. If this is the case, even without confinement, one may be able to discuss chiral symmetry breaking in QCD, as is the SD approach.
At the one-loop level of renormalization-group improvement, the SD kernel is approximated as

and the Landau-gauge gluon propagator is given as

Then, by taking Dirac trace or the trace after multiplying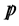


with the bare quark mass 
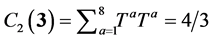
We use one-loop level renormalization-group-improved coupling in the case of 

Figure 1. The Schwinger-Dyson equation for the quark field. The shaded blob denotes the self-energy of the quark


with an infrared regularization of a simple cut at 

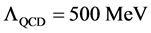


The Higashijima-Miransky approximation is to take the larger value of the argument (Euclidean momenta) in the coupling as



where the Wick rotation has been taken. (For the detail, see, e.g., Appendix in Ref. [73] .) The result of the SD equation is shown in Figure 3 in the chiral limit


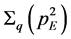
Figure 2. The behavior of the running coupling of our model 
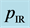
Figure 3. The quark self-energy 
unchanged even the cutoff is taken 10 GeV. The quark mass is large at the infrared region and monotonously goes to zero with the momentum, which reflects spontaneous chiral-symmetry breaking [2] - [4] [88] .
The scale parameter 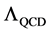

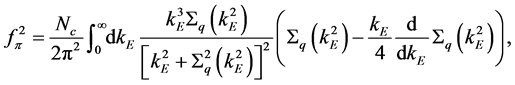
and the (unrenormalized) chiral condensate:

Since the pion decay constant is a physical value, its renormalization is not required and it does not depend on the ultraviolet cutoff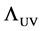



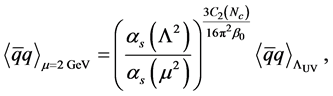
with 

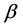




respectively. We have numerically checked that they are stable against the variation of the ultraviolet cutoff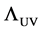
3. The Schwinger-Dyson Equation for the Scalar Diquark
In this section, we investigate the scalar diquark, i.e., an extended colored scalar object, and its mass generation, using the Schwinger-Dyson (SD) formalism.
Diquark is a bound-state-like object of two quarks and decomposed into color anti-triplet 






diquark as an effective degree of freedom with a peculiar size, assuming it to be an extended scalar field 

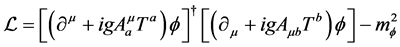
where the bare diquark mass 
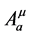


Figure 4. The two types of gluonic interaction for a diquark: (a) inter-two-quarks gluonic interaction to form a diquark and (b) gluonic dressing for the diquark due to its non-zero color charge. The single line denotes a quark, the double line a diquark and the curly line a gluon.
ed. We note that the scalar diquark has the 4-point interaction term of 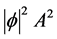
Since the diquark is a bound-state-like object confined in a hadron, it must have an effective size and its size should be smaller than the hadron. In order to include the size effect of diquark, we introduce a simple “form factor” in the four-dimensional Euclidean space as

where the momentum cutoff 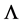
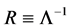
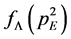
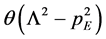

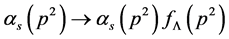
While the scalar QCD Lagrangian (11) is renormalizable, this theory is an effective cutoff theory with an UV cutoff parameter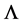



single quark case, presented in the previous section. For instance, we will use the same running coupling 
We now describe the SD equation for the scalar diquark, as shown in Figure 5. For the self-energy diagram, we include the first order of the coupling 
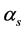

Figure 5. The Schwinger-Dyson equation for the scalar diquark. The shaded blob is the self-energy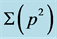
In the right-hand side of Equation (13), the second term arises from the 4-point vertex and the third term is lead from the 3-point vertex, as shown in Figure 5. Here, we do not consider the wave functional renor- malization, as is often assumed for the quark field in the Landau gauge. Similarly in the single quark case, we adopt the Higashijima-Miransky approximation 


4. Numerical Results and Discussion
4.1. The Parameter Setting
The bare mass 
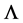
The diquark is originally made of two consistent quarks, and the color-Coulomb interaction is one of the main attractive forces. We here estimate the color-Coulomb interaction between the two massive quarks from the
three-quark (3Q) potential [99] , or generally from the mult-quark potential such as 4Q(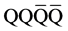


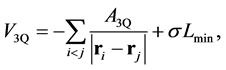
with the color-Coulomb coefficient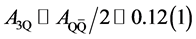

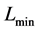
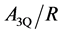
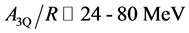
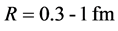
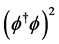

In this paper, we consider two cases of the bare diquark mass. One is twice of constituent quark mass, i.e.,

is determined by the SD equation for single quark Equation (7). This means that the diquark is constructed by the two dressing quarks. The constant bare mass case is based on the constituent quark model like picture and the running bare mass case is the SD formalism with omitting the effect of the gluonic attraction force between two quarks. The diquark should be dressed by gluon furthermore because of its non-zero color charge.
The cutoff 

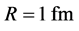

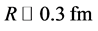

4.2. The Constant Bare Mass Case
We first show in Figure 6 the case of the constant bare mass 





The scalar QCD includes both 3-point and 4-point interactions, and the existence of 4-point interaction is diagrammatically different from the ordinary QCD. To see the role of each interaction, we consider the calculation of the artificial removal of 3-point interaction and 4-point interaction, respectively. In fact, we investigate the two cases: (a) removal of 4-point interaction and (b) removal of 3-point interaction. The result is shown in Figure 7 in the case of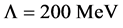

Figure 6. The scalar diquark self-energy 







Figure 7. The self-energy 


diquark without 4-point interaction term is analogous to the quark SD equation, the behavior is completely
different from the quark case. The diquark self-energy 


SD equation without 3-point interaction just rises the self-energy and keeps constant. The strong dependence of the cutoff 
4.3. The Running Bare Mass Case
We show in Figure 8 the case of the running bare mass 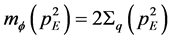


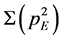



4.4. Discussion on the Scalar Diquark Property
In this subsection, we discuss the mass and the size of the scalar diquark, with comparing to the chiral quark. One of the most important properties of single quark SD equation (7) is the existence of the trivial solution 


On the other hand, the SD equation (13) for scalar diquark has no trivial solution and is a highly non-linear equation, even in the zero bare mass limit
Actually, the scalar diquark self-energy 
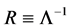
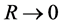

As a quantitative argument, our calculations show that the “compact diquark” with 
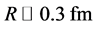
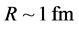
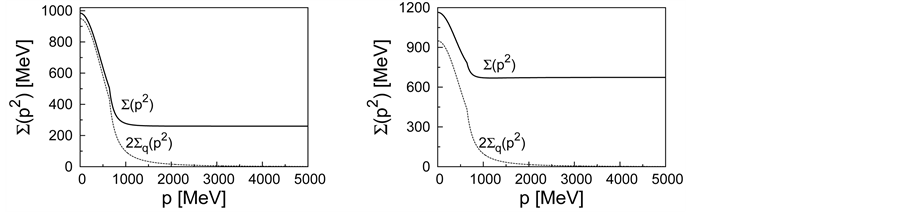
Figure 8. The scalar diquark self-energy 




4.5. Mass Generation for Colored Scalar Particle
Finally, we consider the zero bare-mass case of diquark,

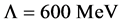

finite and takes a large value even for
of an effective scalar diquark field 
original diquark is constructed by two chiral quarks. Nevertheless, the effective mass of diquark emerges by the non-perturbative gluonic effect. In fact, the mechanism of dynamical mass generation seems to work in the
scalar diquark theory, even without chiral symmetry breaking. If we take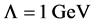

5. Conclusion and Discussion
We have studied various mass generation of colored particles and gluonic dressing effect in a non-perturbative manner, using the Schwinger-Dyson (SD) formalism in QCD. First, we have briefly reviewed dynamical quark-mass generation in QCD in the SD approach as a typical fermion-mass generation via spontaneous chiral-symmetry breaking. Second, using the SD formalism for scalar QCD, we have investigated the scalar diquark, a bound-state-like object of two quarks, and its mass generation, which is clearly non-chiral-origin. Considering the possible size of the diquark inside a hadron, the effect of diquark size R is introduced as a cutoff
parameter 
The basic technology of scalar SD formalism is imported from the single quark case, such as the running coupling, the approximations and so on. Since the diquark is located in and construct of a hadron, the size should be smaller than the hadron (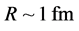

bare mass 


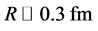
We find that the effective diquark mass is finite and large even for the zero bare-mass case, and the value strongly depends on the size R, which is an example of dynamical mass generation by the gluonic effect, without chiral symmetry breaking. The mass difference between current and constituent charm quark mass and the large glueball mass are also examples of this type of mass generation. In this sense, spontaneous chiral-symmetry breaking may be a special case of massless (or small mass) fermion. As was conjectured in Ref. [10] , it would be a general property of strong interacting theory that all colored particles acquire a large effective mass by the dressing effect, as shown in Figure 10.
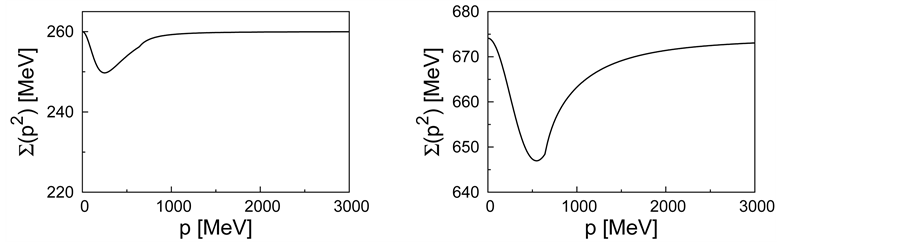
Figure 9. The scalar diquark self-energy 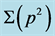


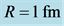



Figure 10. The schematic picture for dynamical mass generation of the colored particle. The colored particle (solid line) interacting with the gluons (curly line). The effective mass emerges by the non-perturbative interaction even without the chiral symmetry.
In this study, we have mainly investigated the diquark properties, and have not calculated physical quantities. It is however desired to describe the color-singlet states such as heavy baryon 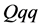

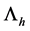


The tetra-quark states 
Acknowledgements
S.I. thanks T.M. Doi, H. Iida and N. Yamanaka for useful discussion and comments. This work is in part sup- ported by the Grant for Scientific Research [Priority Areas “New Hadrons” (E01:21105006), (C) No.23540306, No.15K05076] from the Ministry of Education, Culture, Science and Technology of Japan.
Cite this paper
Shotaro Imai,Hideo Suganum, (2016) Non-Perturbative Analysis of Various Mass Generation by Gluonic Dressing Effect with the Schwinger-Dyson Formalism in QCD. Journal of Modern Physics,07,790-805. doi: 10.4236/jmp.2016.78073
References
- 1. Olive, K.A., et al., Particle Data Group (2014) Chinese Physics, C38, Article ID: 090001.
- 2. Nambu, Y. and Jona-Lasinio, G. (1961) Physical Review, 122, 345.
http://dx.doi.org/10.1103/PhysRev.122.345
Nambu, Y. and Jona-Lasinio, G. (1961) Physical Review, 124, 246. http://dx.doi.org/10.1103/PhysRev.124.246 - 3. Miransky, V.A. (1983) Soviet Journal of Nuclear Physics, 38, 280.
Miransky, V.A. (1994) Dynamical Symmetry Breaking in Quantum Field Theories. World Sicentific, Singapore. - 4. Higashijima, K. (1984) Physical Review, D29, 1228.
http://dx.doi.org/10.1103/PhysRevD.29.1228 Higashijima, K. (1991) Progress of Theoretical Physics Supplement, 104, 1.
http://dx.doi.org/10.1143/PTPS.104.1 - 5. Iritani, T., Suganuma, H. and Iida, H. (2009) Physical Re-view, D80, Article ID: 114505.
http://dx.doi.org/10.1103/PhysRevD.80.114505 - 6. Mandula, J. and Ogilvie, M. (1987) Physics Letters, B185, 127.
http://dx.doi.org/10.1016/0370-2693(87)91541-3 - 7. Amemiya, K. and Suganuma, H. (1999) Physical Review, D60, Article ID: 114509.
http://dx.doi.org/10.1103/PhysRevD.60.114509
Gongyo, S. and Suganuma, H. (2013) Physical Review, D87, Article ID: 074506.
http://dx.doi.org/10.1103/PhysRevD.87.074506
Gongyo, S., Iritani, T. and Suganuma, H. (2012) Physical Review, D86, Article ID: 094018.
http://dx.doi.org/10.1103/PhysRevD.86.094018 - 8. Morningstar, C.J. and Peardon, M.J. (1999) Physical Review, D60, Article ID: 034509.
http://dx.doi.org/10.1103/PhysRevD.60.034509 - 9. Ishii, N., Suganuma, H. and Matsufuru, H. (2002) Physical Review, D66, Article ID: 094506.
http://dx.doi.org/10.1103/PhysRevD.66.094506 - 10. Iida, H., Suganuma, H. and Takahashi, T.T. (2007) Physical Review, D75, Article ID: 114503
http://dx.doi.org/10.1103/PhysRevD.75.114503
Iida, H., Suganuma, H. and Takahashi, T.T. (2007) Modern Physics Letters, A23, 2344
Iida, H., Suganuma, H. and Takahashi, T.T. (2008) AIP Conference Proceedings, 915, 256.
http://dx.doi.org/10.1063/1.2750775 - 11. Brambilla, N., et al. (2011) The European Physical Journal C, 71, 1534.
http://dx.doi.org/10.1140/epjc/s10052-010-1534-9 - 12. Cho, S., et al., ExHIC Collaboration (2011) Physical Review Letters, 106, Article ID: 212001.
http://dx.doi.org/10.1103/PhysRevLett.106.212001 - 13. Aaij, R., et al., LHCb Collaboration (2015) Physical Review Letters, 115, Article ID: 072001.
http://dx.doi.org/10.1103/PhysRevLett.115.072001 - 14. Lichtenberg, D. and Tassie, L. (1967) Physical Review, 155, 1601.
http://dx.doi.org/10.1103/PhysRev.155.1601 - 15. Ida, M. and Kobayashi, R. (1966) Progress of Theoretical Physics, 36, 846-847.
http://dx.doi.org/10.1143/PTP.36.846 - 16. De Rujula, A., Georgi, H. and Glashow, S. (1975) Physical Review D, 12, 147.
http://dx.doi.org/10.1103/PhysRevD.12.147 - 17. DeGrand, T.A., Jaffe, R., Johnson, K. and Kiskis, J. (1975) Physical Review D, 12, 2060.
http://dx.doi.org/10.1103/PhysRevD.12.2060 - 18. Jaffe, R. (2005) Physics Reports, 409, 1-45, http://dx.doi.org/10.1016/j.physrep.2004.11.005
Jaffe, R. (2005) Nuclear Physics B-Proceedings Supplements 142, 343-355.
http://dx.doi.org/10.1016/j.nuclphysbps.2005.01.058 - 19. Close, F. (2005) International Journal of Modern Physics A, 20, 5156.
http://dx.doi.org/10.1142/S0217751X05028661 - 20. Jaffe, R.L. (1977) Physical Review D, 15, 267.
http://dx.doi.org/10.1103/PhysRevD.15.267 - 21. Maiani, L., Piccinini, F., Polosa, A. and Riquer, V. (2005) Physical Review D, 71, Article ID: 014028.
http://dx.doi.org/10.1103/PhysRevD.71.014028 - 22. Ding, G.-J. and Yan, M.-L. (2006) Physics Letters B, 643, 33-40.
http://dx.doi.org/10.1016/j.physletb.2006.10.022 - 23. Zhang, A., Huang, T. and Steele, T. (2007) Physical Review D, 76, Article ID: 036004.
http://dx.doi.org/10.1103/PhysRevD.76.036004 - 24. Lee, H.-J. (2006) The European Physical Journal A, 30, 423-426.
http://dx.doi.org/10.1140/epja/i2006-10104-y - 25. Heupel, W., Eichmann, G. and Fischer, C.S. (2012) Physics Letters B, 718, 545-549.
http://dx.doi.org/10.1016/j.physletb.2012.11.009 - 26. Alford, M.G. and Jaffe, R. (2000) Nuclear Physics B, 578, 367-382.
http://dx.doi.org/10.1016/S0550-3213(00)00155-3 - 27. Suganuma, H., Tsumura, K., Ishii, N. and Okiharu, F. (2007) Progress of Theoretical Physics Supplement, 168, 168- 172.
http://dx.doi.org/10.1143/PTPS.168.168 - 28. Prelovsek, S., Draper, T., Lang, C.B., Limmer, M., Liu, K.-F., Mathur, N. and Mohler, D. (2010) Physical Review D, 82, Article ID: 094507.
http://dx.doi.org/10.1103/PhysRevD.82.094507 - 29. Wakayama, M., et al., SCALAR Collaboration (2015) Physical Review D, 91, Article ID: 094508.
http://dx.doi.org/10.1103/PhysRevD.91.094508 - 30. Alexandrou, C., Daldrop, J.O., Brida, M.D., Gravina, M., Scorzato, L., Urbach, C. and Wagner, M. (2013) Journal of High Energy Physics, 1304, 137.
http://dx.doi.org/10.1007/JHEP04(2013)137 - 31. Chen, H.-X., Hosaka, A. and Zhu, S.-L. (2007) Physical Review D, 76, Article ID: 094025.
http://dx.doi.org/10.1103/PhysRevD.76.094025
Chen, H.-X., Hosaka, A. and Zhu, S.-L. (2007) Physics Letters B, 650, 369-372.
http://dx.doi.org/10.1016/j.physletb.2007.05.031
Chen, H.-X., Hosaka, A. and Zhu, S.-L. (2006) Physical Review D, 74, Article ID: 054001.
http://dx.doi.org/10.1103/PhysRevD.74.054001 - 32. Chen, H.-X., Hosaka, A., Toki, H. and Zhu, S.-L. (2010) Physical Review D, 81, Article ID: 114034.
http://dx.doi.org/10.1103/PhysRevD.81.114034 - 33. Sugiyama, J., Nakamura, T., Ishii, N., Nishikawa, T. and Oka, M. (2007) Physical Review D, 76, Article ID: 114010.
http://dx.doi.org/10.1103/PhysRevD.76.114010 - 34. Fariborz, A.H., Jora, R. and Schechter, J. (2008) Physical Review D, 77, Article ID: 094004.
http://dx.doi.org/10.1103/PhysRevD.77.094004 - 35. 't Hooft, G., Isidori, G., Maiani, L., Polosa, A. and Riquer, V. (2008) Physics Letters B, 662, 424-430.
http://dx.doi.org/10.1016/j.physletb.2008.03.036 - 36. Rosner, J.L. (2007) Physical Review D, 75, Article ID: 013009.
http://dx.doi.org/10.1103/PhysRevD.75.013009 - 37. Guo, X.-H., Thomas, A.W. and Williams, A.G. (1999) Physical Review D, 59, Article ID: 116007.
http://dx.doi.org/10.1103/PhysRevD.59.116007 - 38. Weng, M.-H., Guo, X.-H. and Thomas, A. (2011) Physical Review D, 83, Article ID: 056006.
http://dx.doi.org/10.1103/PhysRevD.83.056006 - 39. Mehen, T. and Tiburzi, B.C. (2006) Physical Review D, 74, Article ID: 054505.
http://dx.doi.org/10.1103/PhysRevD.74.054505 - 40. Selem, A. and Wilczek, F. (2005) Ha-dron Systematics and Emergent Diquarks. Proceedings of Ringberg Workshop on New Trends in HERA Physics, Ringberg Castle, Tegernsee, Germany, 2-7 Oct 2005. arXiv:hep-ph/0602128
http://inspirehep.net/record/710535 - 41. Hernandez, E., Nieves, J. and Verde-Velasco, J. (2008) Physics Letters B, 666, 150-154.
http://dx.doi.org/10.1016/j.physletb.2008.07.007 - 42. Kim, K., Jido, D. and Lee, S.H. (2011) Physical Review C, 84, Article ID: 025204.
http://dx.doi.org/10.1103/PhysRevC.84.025204
Kim, K., Jido, D. and Lee, S.H. (2013) Few-Body Systems, 54, 271-274.
http://dx.doi.org/10.1007/s00601-012-0343-0 - 43. Martynenko, A. and Saleev, V. (1996) Physics Letters B, 385, 297-303.
http://dx.doi.org/10.1016/0370-2693(96)00848-9 - 44. Gomshi Nobary, M. and Sepahvand, R. (2007) Physical Review D, 76, Article ID: 114006.
http://dx.doi.org/10.1103/PhysRevD.76.114006 - 45. Ebert, D., Feldmann, T., Kettner, C. and Reinhardt, H. (1998) International Journal of Modern Physics A, 13, 1091.
http://dx.doi.org/10.1142/S0217751X98000482
Ebert, D., Faustov, R. and Galkin, V. (2011) Physical Review D, 84, Article ID: 014025.
http://dx.doi.org/10.1103/PhysRevD.84.014025 - 46. Jaffe, R.L. and Wilczek, F. (2003) Physical Review Letters, 91, Article ID: 232003.
http://dx.doi.org/10.1103/PhysRevLett.91.232003 - 47. Lee, S.H. and Yasui, S. (2009) The European Physical Journal C, 64, 283.
http://dx.doi.org/10.1140/epjc/s10052-009-1140-x
Lee, S.H., Yasui, S., Liu, W. and Ko, C.M. (2008) The European Physical Journal C, 54, 259-265.
http://dx.doi.org/10.1140/epjc/s10052-007-0516-z - 48. Shuryak, E. and Zahed, I. (2004) Physics Letters B, 589, 21-27.
http://dx.doi.org/10.1016/j.physletb.2004.03.019 - 49. Hong, D.K., Sohn, Y.J. and Zahed, I. (2004) Physics Letters B, 596, 191-199.
http://dx.doi.org/10.1016/j.physletb.2004.06.073 - 50. Karliner, M. and Lipkin, H.J. (2003) Physics Letters B, 575, 249-255.
http://dx.doi.org/10.1016/j.physletb.2003.09.062 - 51. Hyodo, T., Liu, Y.-R., Oka, M., Sudoh, K. and Yasui, S. (2013) Physics Letters B, 721, 56-60.
http://dx.doi.org/10.1016/j.physletb.2013.02.045 - 52. Yasui, S. and Oka, M. (2007) Physical Review D, 76, Article ID: 034009.
http://dx.doi.org/10.1103/PhysRevD.76.034009 - 53. Bacchetta, A., Conti, F. and Radici, M. (2008) Physical Review D, 78, Article ID: 074010.
http://dx.doi.org/10.1103/PhysRevD.78.074010 - 54. Lichtenberg, D., Namgung, W., Predazzi, E. and Wills, J. (1982) Physical Review Letters, 48, 1653.
http://dx.doi.org/10.1103/PhysRevLett.48.1653 - 55. Ferretti, J., Vassallo, A. and Santopinto, E. (2011) Physical Review C, 83, Article ID: 065204.
http://dx.doi.org/10.1103/PhysRevC.83.065204 - 56. Nagata, K. and Hosaka, A. (2004) Progress of Theoretical Physics, 111, 857-870.
http://dx.doi.org/10.1143/PTP.111.857 - 57. Fredriksson, S., Jandel, M. and Larsson, T. (1982) Zeitschrift für Physik C Particles and Fields, 14, 35-39.
http://dx.doi.org/10.1007/BF01547961 - 58. Alexandrou, C., de Forcrand, P. and Lucini, B. (2006) Physical Re-view Letters, 97, Article ID: 222002.
http://dx.doi.org/10.1103/PhysRevLett.97.222002 - 59. Babich, R., Garron, N., Hoelbling, C., Howard, J., Lellouch, L. and Rebbi, C. (2007) Physical Review D, 76, Article ID: 074021. http://dx.doi.org/10.1103/PhysRevD.76.074021
- 60. DeGrand, T., Liu, Z. and Schaefer, S. (2008) Physical Review D, 77, Article ID: 034505.
http://dx.doi.org/10.1103/PhysRevD.77.034505 - 61. Hess, M., Karsch, F., Laermann, E. and Wetzorke, I. (1998) Physical Review D, 58, Article ID: 111502.
http://dx.doi.org/10.1103/PhysRevD.58.111502 - 62. Alford, M.G., Schmitt, A., Rajagopal, K. and Schäfer, T. (2008) Reviews of Modern Physics, 80, 1455.
http://dx.doi.org/10.1103/RevModPhys.80.1455 - 63. Imai, S., Toki, H. and Weise, W. (2013) Nuclear Physics A, 913, 71-102.
http://dx.doi.org/10.1016/j.nuclphysa.2013.06.001 - 64. Ratti, C. and Weise, W. (2004) Physical Review D, 70, Article ID: 054013.
http://dx.doi.org/10.1103/PhysRevD.70.054013 - 65. Harada, M., Nonaka, C. and Yamaoka, T. (2010) Physical Review D, 81, Article ID: 096003.
http://dx.doi.org/10.1103/PhysRevD.81.096003 - 66. Splittorff, K., Toublan, D. and Verbaarschot, J. (2002) Nuclear Physics B, 620, 290-314.
http://dx.doi.org/10.1016/S0550-3213(01)00536-3 - 67. Hands, S., Kim, S. and Skullerud, J.-I. (2007) The European Physical Journal A, 31, 787-789.
http://dx.doi.org/10.1140/epja/i2006-10173-x - 68. Kogut, J.B., Toublan, D. and Sinclair, D.K. (2001) Physics Letters B, 514, 77-87.
http://dx.doi.org/10.1016/S0370-2693(01)00586-X - 69. Strodthoff. N., Schaefer. B.-J. and von Smekal, L. (2012) Physical Review D, 85, Article ID: 074007.
http://dx.doi.org/10.1103/PhysRevD.85.074007 - 70. Alkofer, R. and von Smekal, L. (2001) Physics Reports, 353, 281-465.
http://dx.doi.org/10.1016/S0370-1573(01)00010-2 - 71. Maris, P. and Roberts, C.D. (2003) International Journal of Modern Physics E, 12, 297.
http://dx.doi.org/10.1142/S0218301303001326 - 72. Roberts, C.D. and Williams, A.G. (1994) Progress in Particle and Nuclear Physics, 33, 477-575.
http://dx.doi.org/10.1016/0146-6410(94)90049-3 - 73. Aoki, K.-I., Bando, M., Kugo, T., Mitchard, M.G. and Nakatani, H. (1990) Progress of Theoretical Physics, 84, 683- 701. http://dx.doi.org/10.1143/ptp/84.4.683
- 74. Kugo, T. and Mitchard, M.G. (1992) Physics Letters B, 286, 355-364.
http://dx.doi.org/10.1016/0370-2693(92)91787-A - 75. Fischer, C.S. (2006) Journal of Physics G: Nuclear and Particle Physics, 32, R253.
http://dx.doi.org/10.1088/0954-3899/32/8/R02 - 76. Munczek, H. (1995) Physical Review D, 52, 4736.
http://dx.doi.org/10.1103/PhysRevD.52.4736 - 77. Yamanaka, N., Doi, T.M., Imai, S. and Suganuma, H. (2013), Physical Review D, 88, Article ID: 074036.
http://dx.doi.org/10.1103/PhysRevD.88.074036
Yamanaka, N., Imai, S., Doi, T.M. and Suganuma, H. (2014) Physical Review, D, 89, Article ID: 074017.
http://dx.doi.org/10.1103/PhysRevD.89.074017 - 78. Imai, S. and Suganuma, H. (2013) A Non-Perturbative Effect of Gluons for Scalar Diquark in the Schwinger-Dyson Formalism. Proceedings of XV International Conference on Hadron Spectroscopy. arXiv:1401.3099 [hep-ph]
http://inspirehep.net/record/1277087 - 79. Cheng, T.-P. and Li, L.-F. (1988) Gauge Theory of Elementary Particle Physics. Oxford University Press, Oxford.
- 80. Peskin, M.E. and Schroeder, D.V. (1995) An Introduction to Quantum Field Theory (Frontiers in Physics). Westview Press, Boulder.
- 81. Aad, G. et al., ATLAS Collaboration (2012) Physics Letters B, 716, 1-29.
http://dx.doi.org/10.1016/j.physletb.2012.08.020 - 82. Maas, A. (2011) The European Physical Journal C, 71, 1548.
http://dx.doi.org/10.1140/epjc/s10052-011-1548-y
Maas, A. and Mufti, T. (2014) Journal of High Energy Physics, 1404, 006. - 83. Macher, V., Maas, A. and Alkofer, R. (2012) Inter-national Journal of Modern Physics A, 27, Article ID: 1250098.
http://dx.doi.org/10.1142/S0217751X12500984 - 84. Hopfer, M. and Alkofer, R. (2013) Acta Physica Polonica B Proceedings Supplement, 6, 929.
- 85. Iida, H., Oka, M. and Suganuma, H. (2005) The European Physical Journal A, 23, 305-315.
http://dx.doi.org/10.1140/epja/i2004-10082-0 - 86. Doi, T.M., Suganuma, H. and Iritani, T. (2014) Physical Review D, 90, Article ID: 094505.
http://dx.doi.org/10.1103/PhysRevD.90.094505
Doi, T.M., Redlich, K., Sasaki, C. and Suganuma, H. (2015) Physical Review D, 92, Article ID: 094004.
http://dx.doi.org/10.1103/PhysRevD.92.094004
Suganuma, H., Doi, T.M. and Iritani, T. (2016) Progress of Theoretical and Experimental Physics, 2016, Article ID: 013B06.
http://ptep.oxfordjournals.org/content/2016/1/013B06 - 87. Iritani, T. and Suganuma, H. (2014) Progress of Theoretical and Experimental Physics, 2014, Article ID: 033B03.
Gongyo, S., Iritani, T. and Suganuma, H. (2012) Physical Review D, 86, Article ID: 034510.
http://dx.doi.org/10.1103/PhysRevD.86.034510 - 88. Hatsuda, T. and Kunihiro, T. (1994) Physics Reports, 247, 221-367.
http://dx.doi.org/10.1016/0370-1573(94)90022-1 - 89. Pagel, H. and Stokar, S. (1979) Physical Review D, 20, 2947.
http://dx.doi.org/10.1103/PhysRevD.20.2947 - 90. 't Hooft, G. (1976) Physical Review D, 14, 3432.
http://dx.doi.org/10.1103/PhysRevD.14.3432 - 91. Schäfer, T. and Shuryak, E.V. (1998) Reviews of Modern Physics, 70, 323.
http://dx.doi.org/10.1103/RevModPhys.70.323 - 92. Itzykson, C. and Zuber, J.-B. (2006) Quantum Field Theory. Dover Publications, Mineola.
- 93. Marinho, J., Gambin, E. and Frederico, T. (2007) AIP Conference Proceedings, 884, 378.
http://dx.doi.org/10.1063/1.2710608 - 94. Salam, A. and Strathdee, J. (1978) Physical Review D, 18, 4713.
http://dx.doi.org/10.1103/PhysRevD.18.4713 - 95. Bender, A., Roberts, C.D. and Von Smekal, L. (1996) Physics Letters B, 380, 7-12.
http://dx.doi.org/10.1016/0370-2693(96)00372-3 - 96. Cahill, R., Roberts, C.D. and Praschifka, J. (1987) Physical Review D, 36, 2804.
http://dx.doi.org/10.1103/PhysRevD.36.2804 - 97. Wang, Z., Wan, S. and Yang, W. (2007) Communications in Theoretical Physics, 47, 287.
http://dx.doi.org/10.1088/0253-6102/47/2/020 - 98. Bloch, J.C., Roberts, C.D., Schmidt, S., Bender, A. and Frank, M. (1999) Physical Review C, 60, Article ID: 062201.
http://dx.doi.org/10.1103/PhysRevC.60.062201
Bloch, J.C., Roberts, C.D. and Schmidt, S. (1999) Physical Review C, 60, Article ID: 065208.
http://dx.doi.org/10.1103/PhysRevC.60.065208 - 99. Takahashi, T.T., Matsufuru, H., Nemoto, Y. and Suganuma, H. (2001) Physical Review Letters, 86, 18.
http://dx.doi.org/10.1103/PhysRevLett.86.18
Takahashi, T.T., Suganuma, H., Nemoto, Y. and Matsufuru, H. (2002) Physical Review D, 65, Article ID: 114509.
http://dx.doi.org/10.1103/PhysRevD.65.114509 Sakumichi, N. and Suganuma, H. (2015) Physical Review D, 92, Article ID: 034511.
http://dx.doi.org/10.1103/PhysRevD.92.034511 - 100. Okiharu, F., Suganuma, H. and Takahashi, T.T. (2005) Physical Review Letters, 94, Article ID: 192001.
http://dx.doi.org/10.1103/PhysRevLett.94.192001
Okiharu, F., Suganuma, H. and Takahashi, T.T. (2005) Physical Review D, 72, Article ID: 014505. http://dx.doi.org/10.1103/PhysRevD.72.014505