Received 8 January 2016; accepted 14 February 2016; published 17 February 2016

ABSTRACT

Squeezed quantum vacua seems to violate the averaged null energy conditions (ANEC’s), because they have a negative energy density. When treated as a perfect fluid, rapidly rotating Casimir plates will create vorticity in the vacuum bounded by them. The geometry resulting from an arbitrarily extended Casimir plates along their axis of rotation is similar to van Stockum spacetime. We observe closed timelike curves (CTC’s) forming in the exterior of the system resulting from frame dragging. The exterior geometry of this system is similar to Kerr geometry, but because of violation of ANEC, the Cauchy horizon lies outside the system unlike Kerr blackholes, giving more emphasis on whether spacetime is multiply connected at the microscopic level.

Keywords:

Closed Timelike Curves, Multiply Connected Spacetime, Casimir Vacuum, Energy Conditions

1. Introduction

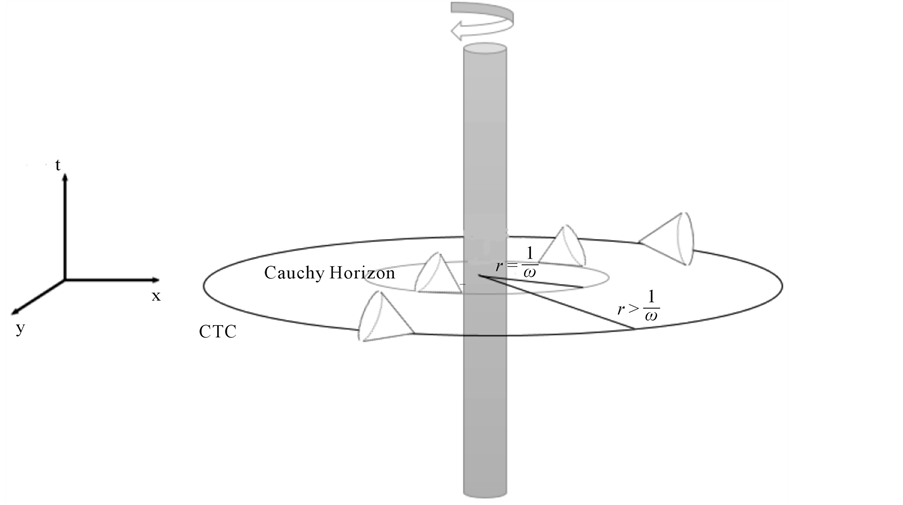
If we examined the compatibility of squeezed vacuum energy with the energy conditions imposed by general relativity we notice a clear violation of them by the squeezed vacuum [1] . Thus squeezed vacuum behaves like an exotic matter. It is tempting to link the violation of ANEC’s by squeezed vacua and their geometric back reaction. We can “stir” the squeezed vacuum by letting the Casimir plates (or general boundary condition) rotate [2] . This rotation should remove the pressure on the plates and create an effect analogous to vorticity in fluids. We calculated the geometry resulting from this system and the conditions that should be satisfied to create the closed timelike curves (CTC’s) near the system (Figure 1). This calculation ignores however the quantum vacuum in the exterior, it is conjectured that the exterior vacuum will prevent the formation of CTC’s [3] . In our calculation we demonstrate other possible effects that might save chronology in this setup. Nevertheless, this system is a good example of how quantum vacuum is needed to stabilise geometry. Finally, we proposed a method for maintenance of traversable wormholes using the rotating Casimir plates.

2. Vorticity of Squeezed Vacua

Consider a scalar quantum field,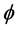. With boundary conditions created by Casimir plates separated by a dis- tance L on the x-axis. In an arbitrary curved spacetime, the expectation value of the normally-ordered stress- energy tensor is given by [4] :

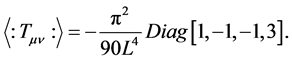(1)

This result comes from zeta regularisation of the expression:

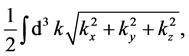(2)

since the boundary conditions are in x-axis we write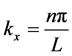. However, the expression above is independent of

which coordinates we take into consideration, or even if we assumed that the plates are arbitrary oriented in the

x − y plane, i.e.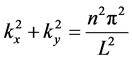. Moreover, the value will not change even if we let the plates rotate around the

z-axis with an angular speed, see Figure 1. What would change however is the polarisation of the squeezed vacuum. The direction in which the refractive index is more than unity and photons propagating between the

plates will experience Scharnhorst effect. If we let 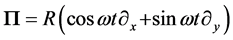be the vector representing pola-

risation of the squeezed vacuum. Where and 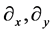are vector fields in the x and y directions respec-

tively. If we considered the time derivative of this polarisation vector we get:

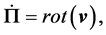(3)

here 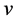is the tangential velocity vector. The expression (3), is the definition of vorticity vector of a fluid. Light paths between the rotating plates would look like spirals in spacetime as shown in Figure 2. Now, we impose yet another condition on the system to get a pressureless vacuum or vacuum dust. In order to do that the angular speed of the plates should be:

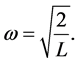(4)

3. Background Geometry of Rotating Squeezed Vacuum

An Ansatz corresponding to the Solution to the Einstein field equations for a pressuresless fluid (dust) with vorticity is made by considering the van Stockum geometry expressed by the frame fields 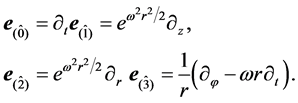[5] :

(5)

The Killing vector fields are, and. We can also write the line element―in cylindrical coor- dinates:

(6)

with coordinate condition:

(7)

But from (1) and (4), we first have. We equate both expressions for the density and get the value angular speed in terms of L. Solution for is given by [6] :

(8)

where w is the Lambert W function. The product 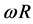which corresponds to the tangential velocity of the plates, should be less than 1 or the solution is meaningless, otherwise we’ll allow the plates to rotate at a tangential velocity greater than the speed of light. This leads to a conclusion that the solution proposed in (6) could be valid when the separation between the plates is comparable to the Compton wavelengths of relativistic elementary particles―like the electron―, at first glimpse. Now we use (4) to get an exact number for the acceptable separation between the plates Å. The result predicts separation within the quantum mechanical realm, not very extreme, where quantum gravity effects are assumed to be.

4. Closed Timelike Curves near the Solution

We focus now on the exterior of the system viz. We examine the spacetime at. The frames are dragged severely such that light cones become tangent to the plane. As we move outward we see that the fames in the light cone become more tilted forming closed timelike curves (CTC’s) around the system. We observe that the circular paths described above are not timelike geodesics. Thus, to enter them an observer must accelerate first. This is similar to the van Stockum solution. Thereby we can classify curves around this system in the following way as shown in Figure 3.

Ÿ Closed Spacelike Curves: Observers will just circle around the rotating system, no particle accelerating from the exterior can ever enter this region.

Ÿ Closed Null Curve (Cauchy Horizon): Only null rays can orbit around the system, it forms a horizon from particle accelerating from the outside.

Ÿ Closed Timelike Curves: particles from the interior can never escape to them, and particles from the outside need to accelerate to maintain in these curves. However if a particle stopped accelerating while in these curves, a very strange thing happens, it might have multiple biographies! Note that the CTC’s lie before the Cauchy horizon with respect to an accelerating observer coming from infinity.

For the calculated separation between the plates the condition is indeed satisfied. Now turn to the quantum effects associated with those CTC’s, they cannot be ignored here as the whole system is rather microscopic. Hawking and Ellis [3] [7] had argued that for a CTC to form, weak energy conditions (or more generally averaged null energy conditions ANEC [8] ) must be violated. If we took our stress-energy tensor (1) and integrated along a loop surrounding the rotating system with respect to an affine parameter a, we get:

(9)

where a one form reduced by our affine parameter. Equation (7) clearly meets the conjecture of Hawking and Ellis regarding energy conditions. This makes the solution physical, the value of vacuum density decreases you let the separation between the plates increase; unlike Tipler’s Cylinder [9] . The second conjecture made by Hawking is that such stress energy tensor cannot create CTC’s on a finite region of spacetime. That implies that the rotating plates mush be infinite in length, this does not appear in the requirement of this solution but for practical purposes, the separation between the plates is extremely small compared to their length―if we picked any length in the classical domain. However, we paid a large price for making CTC’s that seems to defy the Chronology Protection. That is the CTC’s are very small regions that only quantum particles can enter them, the gravitational effects of the rotating system is very small implying the CTC’s has only microscopic effects.

5. Quantum Effects in the CTC’s

Despite the apparent possibility for this system to defy causality, this solution is highly unstable. To illustrate this, we need to study quantum effects resulting in the CTC’s. Let a scalar field and a detector be coupled to that field. We shall calculate the transition amplitude for the detector’s excitation by observing particles created from the field. We start by assuming the field is massless and coupled to the detector via a weak monopole coupling. We care about the coupling term in their Lagrangian where g is small coupling constant and is the time-dependent monopole operator. The detector has an energy states described by the associated Hilbert space. The field has an associated Fock space. We are interested in the transition amplitude from the initial state to the final state of the Hilbert space for the detector and the field. The transition amplitude shall refer to excitation of the detector energy state above initial ground state due to particle creation by the scalar field. Hence it is rather natural to assume the final state in the Fock space would be. We write the first order perturbation term for the transition amplitude:

(10)

where is the proper time of the detector. We may use Heisenberg equation to rewrite the operator as:

(11)

Substituting (11) into (10) to get:

(12)

To calculate the probability, we square the term and sum over the energies:

(13)

where is the response function which is given by:

(14)

It could be interpreted as the Fourier transform of the two-point Wightman function for positive modes:. The task now is to calculate the latter function, which depends on the path the detector follows as it is a function of the proper time. The Wightman function depends on the path the detector follows, since it is a CTC that implies that the proper time is described by a periodic function. That means that the Wightman function for positive frequency could tern to negative frequency one when the detector completes the cycle in the CTC meaning loss of Unitarity. If we considered the detector a fermion coupled with a charge to a field (like the electrodynamic interaction), the detector could be scattered by its past self. Hence the Feynman diagram with two vertices can be written as:

(15a)

(15b)

With identifying the points A with C and B with D. We get a “loop” diagram instead of tree. A question arises here about the Unitarity of such processes, and how can they affect the stability of the system. More detailed argument about QFT in CTCs are made in [6] showing Unitarity loss in further detail. As Figure 4 and Figure 5 demonstrates how tree diagram turns into a loop diagram in CTC’s, since loop diagram appear a lot in self- energy terms of a particle. It is possible that they could be explained by multiple-connectedness of spacetime near their energy scale. The results from this paper seems to support that quantum mechanics implies a multiply- connected spacetime background.

6. Traversable Wormholes Maintenance by Rotating Squeezed Vacuum

Einstein-Rosen bridges does not allow matter/information to be transferred from one mouth to the other. The

ANEC permits them from doing so, as the bridges are not stable and pinch off at the speed of light. When using exotic matter, or stress-energy tensor that violates ANEC like in (9), singularities and horizons are prevented in this case. Such that when passing through one of the wormholes’ mouth, there must be null geodesics with tangent vectors satisfying (9), this can be achieved by the stress-energy of the squeezed vacuum. An example of a static, spherically-symmetric wormhole is given by the line element [8] :

(16)

where l is the proper radial distance from the wormhole’s mouth, i.e. at the mouth. Moreover, is a function of l, that is everywhere finite (no isolated horizon condition), and approximated at a distance far away

from the mouth by. The violation of the ANEC is by the condition [10] :

(17)

where is the tension and is the “exotic” matter density. The rotating Casimir plates provide such energy conditions with the rotation (centrifugal force) canceling out the pressure and balancing the plates. From (1) we have as above, and. Thus, rotating Casimir vacuum can be used to support this wormhole. In order to this, we place the rotating plates, such that the mouth is at the axis of symmetry of the rotating plates. Outside the plates, as we discussed earlier, Kerr geometry is produced satisfying the conditions for that produces CTC’s at the exterior, in order for the system to satisfy Einstein field equations.

7. Discussion

This paper aims to shine the light on the possibility of violating NAEC by quantum field theory and create exotic geometries from them. The setup above showed that we could be able to make quantum time machines by squeezed vacuum. This created problems with the quantum field theory itself regarding Unitarity. Calculations by [6] showed that Unitarity is lost in periodic proper time functions in the correlation function in CTC’s. We could explore this problem further by entangling two particles one in the CTC and the other is away from it. After a while the entanglement would be destroyed as the first particle goes back to the time before it was entangled with the latter. In our rotating plates, we propose that this problem could be resolved by conjecturing that

the system pays for the lost energy/information, as it required energy give approximately by. If

we considered rotating charged Casimir plates we notice that the condition (4) would be modified, and we have less rotating velocity to maintain dust solution, as a result will have a larger Cauchy horizon. The exterior geometry would be similar to the Kerr-Neuman geometry. We notice a pattern or an analogy between blackholes geometry and the one of squeezed vacua. Because of the violation of energy conditions by the squeezed vacua, the Cauchy horizon (CH) lies outside the system unlike blackholes who have the CH inside of them. Since CTC’s could be made from boundary conditions on quantum vacuum, this raises a question about whether CTC’s could form by quantum fluctuations, and the quantum foam is filled with them? In other words, quantum spacetime is multiply-connected.

8. Conclusion

Squeezed vacuum violating ANEC could be used to create quantum time machines by creating microscopic CTC’s and also maintaining traversable wormholes when forcing the boundary conditions (Casimir plates) to rotate at sufficient angular velocity to remove the pressure made by the squeezed vacuum and create vorticity defined by the polarisation of the refractive index between the plates. Vorticity of the squeezed vacuum could be understood by plotting the light trajectory inside the rotating plates that are found to be making spirals in spacetime. The squeezed vacuum has characteristics similar to van-Stockum dust and an advantage above it by violating ANEC that allow CTC’s to form outside the system and a disadvantage of only making CTC’s at the microscale. This solution resulting from semi-classical general relativity, but also appears to violate Unitarity; in the future we aim to investigate in detail the quantum effects appearing in such CTC’s and whether they could allow this solution to be stable or not. From fundamental point of view, this solution could demonstrate that the quantum spacetime is multiply connected, and unitarity is saved if we give up the notion of locality (in space- time).

Acknowledgements

This research project was supported by a grant from the “Research Center of the Female Scientific and Medical Colleges”, Deanship of Scientific Research, King Saud University.

Cite this paper

S. AlSaleh,L. A. AlAsfar,A.Mahroussah, (2016) Rotating Squeezed Vacua as Time Machines. Journal of Modern Physics,07,304-311. doi: 10.4236/jmp.2016.73030

References