Journal of Modern Physics
Vol.07 No.04(2016), Article ID:64053,9 pages
10.4236/jmp.2016.74040
Why Energy and Mass Can Be Converted between Each Other? A New Perspective Based on a Matter Wave Model
Donald C. Chang
Macro-Science Group, Division of LIFS, Hong Kong University of Science and Technology, Hong Kong, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 January 2016; accepted 26 February 2016; published 29 February 2016
ABSTRACT
It was predicted by Einstein that energy and mass can be converted between each other. But why? Energy and mass are two very different physical concepts. How can they be exchanged with each other? We think the key to answer this question is to recall that a particle can behave like a wave. Particle properties like energy and momentum are known to be related to their corresponding wave properties (frequency and wave vector). Mass is clearly a particle property; is it also related to a wave property? This study suggests that it is. We found that mass and energy appear to share similar physical nature in the wave perspective. Both of them are related to the curvature of bending the vacuum medium during the propagation of the excitation wave. This similarity explains why they are convertible.
Keywords:
Energy, Mass, Particle, Wave, Vacuum, Matter Wave, Special Relativity

1. Introduction
Recent studies of cosmology suggest that our universe is not only composed of visible matter; there are also dark matter and dark energy [1] . The visible matter only accounts for about 5% of the content of the universe, while 25% is composed of dark matter, and about 70% is dark energy [1] . At this point, we have very little knowledge about the physical properties of the dark matter and dark energy. In order to find some hints to hunt for the dark matter, perhaps we should thoroughly examine our understanding of the visible matter first.
At this point, there are still many unanswered questions about the visible matter. For example, we know that energy and mass can be converted between each other. But what is its physical basis? This energy-mass conversion was attributed to the Special Theory of Relativity (STR) [2] . That is, energy and mass are related by the famous relationship E = mc2. But why? Energy and mass are very different physical concepts. How can they be convertible? STR only proposed the energy-mass conversion rule; it did not explain the physical foundation of this rule. Thus, it will be interesting to explore ways to explain this rule on a physical basis.
2. The Wave Nature of Sub-Atomic Particles
We think the key to understand energy-mass conversion is to recognize that matter has wave properties. The concept of matter wave was proposed almost a century ago. Phenomenologically, it was found that a particle can behave like a wave or a corpuscular object depending on the situation [3] . This peculiar phenomenon is called “wave-particle duality”. The key question now is about the true physical nature of the particle: Is it a massive point object or a physical wave packet? In the case of photon, there is no question that light is an electro-magnetic wave. But it can behave like a particle (photon) during certain physical interactions, such as in the case of photoelectric effect or Compton scattering [4] . Thus, a packet of electro-magnetic wave can behave like a particle.
Besides light wave, sound waves can also behave like particles. It is well known in condensed matter physics that excitation waves in a solid (or fluid) can be treated like particles (called “phonons”). Phonons can interact with other particles (like electrons) and play a major role in determining the electrical conductivity of many materials [5] .
On the other hand, sub-atomic particles with mass can also behave like waves. It was shown in 1927 that electrons can be diffracted by a nickel crystal [6] . Later, other subatomic particles such as neutrons or helium atoms were also found to behave like wave in diffraction experiments [7] [8] .
The physical nature of matter wave is still not clearly understood today. In most quantum mechanics textbooks, the particle is treated as a pointed object; the wave property is only associated with the probability of finding the particle at a particular space and time. (This is called the “Copenhagen interpretation”) [3] . But in view of the findings of the diffraction experiments, it seems more sensible to regard the particle as a physical wave rather than a probability wave. This point can be demonstrated easily using the example of a radiation wave. We know that light is an electro-magnetic wave; its diffraction pattern can be explained very easily based on such wave properties. But if we regard light as a probability wave of a photon, the explanation will be much more difficult.
Furthermore, we know particles can be created or annihilated in the vacuum. If the particle is a real object, how can it appear from nowhere or disappear suddenly with no trace? The only rational explanation is that the particle is an excitation wave, so that it can be excited by an energetic stimulation and it can be transformed from one type of wave into another type of wave. Therefore, we propose that the so-called “particle” is actually an excitation wave of the vacuum [9] . In another word, the particle is a physical wave in the microscopic view; it behaves like a corpuscular object (particle) only in the macroscopic view.
3. Physical Nature of the Vacuum
If the matter wave is a physical wave, then what is its carrying medium? In the 19th century, the electro-magnetic field was thought to be carried by a medium called “aether” [10] . The aether hypothesis, however, was rejected in the early 20th century due to the following reasons:
1) The mechanical properties of this hypothetical aether were full of contradictions. Aether was supposed to fill all space between matters. Thus, it must be a highly fluidic substance (gas or liquid). Such fluidic medium, however, can only transmit low frequency dilational wave. In order to transmit high frequency transverse wave such as light, the aether must be a rigid solid. These two requirements are contradicting with each other.
2) The aether hypothesis could not explain why large astronomical objects like Earth or Mars can pass through it without experiencing any resistance. This is contradicting to the requirement that aether is a fluid or a solid.
3) The aether hypothesis was not supported by experiments. In late 19th century, many experiments were conducted to detect the motion of aether using optical interferometers [11] . All these experiments failed to detect any movement between aether and the Earth.
4) Later, the aether hypothesis was thought to be unnecessary. Finally in 1905, Einstein proposed the Special Theory of Relativity and showed that one can explain the null results easily without the assumption of aether [2] . With the widely acceptance of STR, the aether hypothesis was abandoned.
Hence, people in the early 20th century believed that the vacuum in our universe is totally empty. But such a view is no longer valid today. With the development of quantum electrodynamics, the vacuum is thought to contain the zero-point energy of all oscillations in the electromagnetic field [10] . In fact, the properties of the vacuum become very complicated in today’s quantum field theory. For example, according to the Dirac theory of electron, the vacuum is filled with an ocean of negative energy electrons. The hole created in this ocean will become the anti-particle, positron [12] . The vacuum thus is far from emptiness. Moreover, since there are many types of anti-particles, if one follows the Dirac theory, it would require the vacuum to be filled with multiple oceans of different types of negative energy fermions. (Note: The Dirac theory is even more troublesome for bosons, which do not follow Pauli’s exclusion principle. Thus, their negative energy states cannot be fully filled.)
In the more recent quantum field theory, a particle is regarded as the excitation of its field. Different types of particles are associated with different fields. However, these fields do not have the same meaning as classical fields. The physical meaning of quantum field is not clear at present. There is still a debate about what is more fundamental: Is it particle or field? Currently there is no agreement on it [13] . Furthermore, such thinking requires a large number of fields for our universe. It is not so beautiful.
Thus, there is a dilemma now. On the one hand, the old concept of aether is unviable. On the other hand, with the development of quantum field theory, the vacuum can no longer be regarded as “emptiness”. What is the way out? We think this dilemma can be solved by assuming that the vacuum is a pre-existing medium in our universe and it fills all space; both matter waves and radiation waves are excitation waves of this medium [14] . In another word, all particles found in nature (with or without mass) are excitation waves of the same vacuum medium.
This new model can overcome all problems of the previous aether hypothesis:
First, we can avoid contradicting mechanical requirements for the vacuum. Since the vacuum is a pre-existing medium occupying the entire universe, not just filling the space between matters, it does not need to be fluidic.
Second, the atoms making up the planet are all waves; there should be no friction between matters and the vacuum. Thus, planets can move within the vacuum medium without dragging.
Third, the null results of the optical interferometer experiments reported by Michelson and Morley (1887) can be easily explained [11] . All one needs is to show that the wave equation describing the excitation waves in the vacuum medium is Lorentz invariant. As we will show in the following, this requirement can indeed be met.
4. The Vacuum Behaves Like a Dielectric System According to the Maxwell Theory
If particles are excitation waves, what is the physical nature of the vacuum medium? At this point, our knowledge about the vacuum is very limited. However, there is a very good hint from the work of Maxwell, who suggested that the vacuum behaves like a dielectric medium [15] . When Maxwell first proposed his equations in 1862, his description of Ampere’s Law was
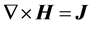 . (1)
. (1)
He later found a problem in it, because this equation would violate the condition of conservation of charge,
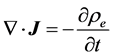 . (2)
. (2)
In order to fix this problem, Maxwell proposed to add a new term 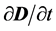 into the right hand-side of Equation (1) [16] . (D is called the “charge displacement”.) The justification for this was that, in a dielectric material, there are both positive and negative charges embedded within the medium. So, when the dielectric medium is exposed to an electric field, it will induce a displacement of the dielectric charges. A time variation of the displaced charge should produce a displacement current (Jd), which can also affect the magnetic field. So that in Equation (1), one should consider not only the externally applied current J, but also the internally induced displacement current Jd. That is
into the right hand-side of Equation (1) [16] . (D is called the “charge displacement”.) The justification for this was that, in a dielectric material, there are both positive and negative charges embedded within the medium. So, when the dielectric medium is exposed to an electric field, it will induce a displacement of the dielectric charges. A time variation of the displaced charge should produce a displacement current (Jd), which can also affect the magnetic field. So that in Equation (1), one should consider not only the externally applied current J, but also the internally induced displacement current Jd. That is
 .
.
Thus, Maxwell thought that the correct form of Ampere’s law should be
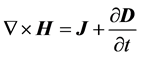 . (1A)
. (1A)
This becomes a part of the final form of the Maxwell’s equations used today.
The addition of a displacement current term was a stroke of genius. This allowed Maxwell to construct his theory of light propagation. When Maxwell investigated the propagation of electro-magnetic waves in the vacuum, he argued that the external current J is zero, but the displacement current term is not zero. This is equivalent to say that he believed the vacuum is a dielectric medium. Thus, Equation (1A) in the vacuum becomes
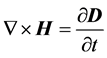 . (1B)
. (1B)
Using this equation, one can easily derive the wave equation for the electro-magnetic wave,
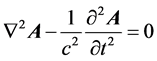 . (3)
. (3)
where A is the vector potential and 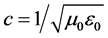 is equal to the speed of light. (ε0 is permittivity and μ0 is permeability in free space). Thus, the key conceptual step in Maxwell’s theory of light propagation was to regard the vacuum as a dielectric medium. If one treats the vacuum as pure emptiness and remove the
is equal to the speed of light. (ε0 is permittivity and μ0 is permeability in free space). Thus, the key conceptual step in Maxwell’s theory of light propagation was to regard the vacuum as a dielectric medium. If one treats the vacuum as pure emptiness and remove the 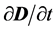 term in Equation (1A), it will not be possible to derive the wave equation of light.
term in Equation (1A), it will not be possible to derive the wave equation of light.
5. What Is the Basic Wave Equation for an Excitation Wave?
If both the radiation waves and matter waves are excitation waves of the same vacuum medium, then waves representing different particles (with or without mass) should obey the same wave equation, which is determined by the physical properties of the vacuum medium. One may be surprised that this point is actually supported by the Special Theory of Relativity. STR predicts that no object can travel faster than the speed of light [2] . This means that the limiting speed of all particles (with or without mass) must be the same. We know that the speed of an excitation wave is determined solely by the physical properties of the transmitting medium [15] . The prediction of STR can be justified only if matter wave and radiation wave are carried by the same vacuum medium.
What is the basic form of this wave equation? At this point, we know the wave equation of at least one particle; that is the photon. This may provide a very useful hint. We know a photon is an oscillating wave of electro-magnetic fields, which are linear functions of the vector potential Aμ = (ϕ, A). If matter waves and radiation waves are both excitation waves of the same vacuum medium, we expect that the wave function of the matter wave ψ may also be a linear function of Aμ. This means that ψ should also obey the same wave function as shown in Equation (3), i.e.,
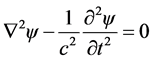 . (4)
. (4)
We propose that this is the basic wave equation for all types of excitation waves of the vacuum medium. ψ can have different solutions, which may represent different types of free particle. (Note: Even though Equation (4) does not look like any wave equations commonly used in quantum mechanics, it is not inconsistent with them. In fact, we can show later in this paper that Equation (4) can be reduced into the Klein-Gordon equation for particles of nonzero mass. By linearizing the Klein-Gordon equation, one can then derive the Dirac equation for electrons [12] . Under the low energy limit, the Schrödinger equation can be obtained.)
6. General Wave Function of a Free Particle
Now let us examine the different solutions of the basic wave equation. The simplest solution of Equation (4) is a plane wave 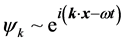 where k and ω are the wave vector and frequency, respectively. We propose that this plane wave solution represents a radiation particle (massless), such as a photon. For a particle with non-zero rest mass, the solution is more complicated. Such a particle would behave like a mass point in the classical limit; thus, the probability of finding the particle should be highest at its trajectory. This suggests that the wave function of a massive particle not only depends on the spatial coordinate along its trajectory (i.e.,
where k and ω are the wave vector and frequency, respectively. We propose that this plane wave solution represents a radiation particle (massless), such as a photon. For a particle with non-zero rest mass, the solution is more complicated. Such a particle would behave like a mass point in the classical limit; thus, the probability of finding the particle should be highest at its trajectory. This suggests that the wave function of a massive particle not only depends on the spatial coordinate along its trajectory (i.e., ), it also varies in the transverse plane (
), it also varies in the transverse plane (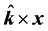 ). Thus, one may assume that the general wave function representing a free particle has the form
). Thus, one may assume that the general wave function representing a free particle has the form
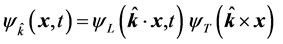 , (5)
, (5)
where 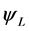 is the longitudinal component of the wave function which describes the travelling wave along the particle’s trajectory, and
is the longitudinal component of the wave function which describes the travelling wave along the particle’s trajectory, and 
where ℓ is a fitting parameter which is subjected to the condition

By solving Equations (6A) and (6B) separately [9] , one can easily show that the general solution of ψ is

where Jn is Bessel function of the first kind; n is an integer or half integer; r and θ represent the radial distance and the azimuthal angle of the space vector in the transverse plane. (a is a normalizing constant.) As expected, the wave function of a free particle behaves like a travelling wave moving along the direction of its trajectory. But due to the presence of the Bessel function, 
7. Physical Meanings of the Wave Parameters
The wave function shown in Equation (8) contains four parameters, ω, k, ℓ and n. What are their physical meanings? Using the correspondence principle 







At

This result makes good sense, since when one substitutes Equation (10) into Equation (7), and recalls that 


which is identical to the energy-momentum relationship implied from STR [2] . By combining Equations (9), (10) and (11), one can further obtain

At

8. Both Energy and Mass Are Related to the Bending Curvature of the Vacuum
Our finding that the rest mass m is related to the parameter ℓ in the wave function has important implication. From Equation (8), we see that the transverse component of the free particle wave function is described by a Bessel function, the asymptotic form of which is

Thus, ℓ can be regarded as the “transverse wave number” of the free particle, i.e., it is the inverse of the wavelength in the transverse oscillation, 
This finding is very interesting; it is closely parallel to the Planck’s relation and the de Broglie relation, which show that the energy and momentum are related to the periodicity of oscillation of the vacuum medium. More specifically, E is related to the periodicity of oscillation in the time dimension, and p is related to the periodicity of oscillation in the spatial dimension along the direction of the trajectory. Our finding that the rest mass is associated with the oscillation periodicity in the transverse direction thus appears to make very good sense. In essence, our result suggests that energy, momentum and mass are all related to the curvature of bending the vacuum medium during the propagation of the excitation wave.
This result is not totally surprising, since both energy and mass must be created by “work”. Before the vacuum is excited by a stimulus, it is in the resting state (ground state). In order to trigger an excitation wave, one must create an energetic disturbance at a local region of the vacuum medium. Since it takes work to bend the vacuum medium, the more sharply the bending curvature, more work is required. This is true for bending the medium in all dimensions (spatial and temporal). Thus, a shorter wavelength of a propagating wave should always associate with a higher “energy state”, which may be reflected in an increase in energy, momentum or “mass” of the excitation wave.
This geometrical interpretation of mass and energy suggests that the physical natures of energy and mass are very similar in the wave perspective. This explains why energy and mass can be converted between each other.
9. A Free Particle with Nonzero Rest Mass Behaves Like a Vortex
Based on the discussions above, we believe that both radiation wave and matter wave are excitation waves of the vacuum medium. The basic wave equation is determined by the physical property of the vacuum medium, which behaves like a dielectric system as suggested by Maxwell. The solution of this wave equation can represent particles of different types. We think the radiation wave is corresponding to the plane wave solution; while the matter waves are represented by the cylindrical wave solutions,

Figure 1. A plot of ψT at the transverse plane for n = 0. The wavelength is denoted λT.
The various wave parameters in this equation represent different particle properties. The wave vector k is related to the momentum p; the frequency ω is related to the energy E; and the transverse wave number ℓ is related to the rest mass m. This wave function represents an excitation wave advancing in helical motion. This can be seen by examining the physical meaning of the parameter n. It appears that n is associated with the helicity of the free particle, since it is a quantum number conjugate to the angular coordinate θ. Dimensional analysis thus suggests that n is associated with some sort of angular momentum. Because of the added phase factor nθ in Equation (8), the wave function representing a free particle actually propagates in a helical fashion (see Figure 2).
We can demonstrate this point more explicitly. Let ω = ω1 + ω2, substituting it into Equation (8), we have

The first exponential term 


10. Our Proposed Wave Equation Is Consistent with Other Quantum Mechanical Equations
In this work, we propose that all particles (with or without mass) are excitation waves of the vacuum medium. The basic wave equation is Equation (4). For particles without mass (i.e., radiation waves), there should be no problem to accept it, since this equation is identical to the wave equation of light. But for particles with rest mass (i.e., matter waves), can Equation (4) properly describe their excitation waves? In relativistic quantum mechanics, the motion of massive particles is usually described by the Klein-Gordon equation [17] [18] or the Dirac equation. Is Equation (4) compatible with these quantum mechanical equations?
In the following, we will show that this is indeed the case. One should keep in mind that in describing the motion of a particle, there are two categories of wave equations. The first category is the basic wave equation which describes all types of excitation waves in the vacuum medium. Different solutions of this wave equation represent different types of particles. The second category is wave equations that describe the motion of a specific type of particle. We propose that Equation (4) belongs to the first category. Since it is applicable to all types of particles, the particle mass should not appear in the equation. For wave equations of the second category, the particle mass can appear in the wave equation, since it describes the motion of a single type of particle. We believe the Klein-Gordon equation or the Dirac equation belong to this category.
The question now is whether one can derive the Klein-Gordon equation or the Dirac equation from the basic wave equation of the vacuum medium (i.e., Equation (4)). As shown in Equation (5), the wave function representing an excitation wave in the vacuum medium has both a longitudinal component (ψL) and a transverse component (ψT). When one substitutes Equation (5) into Equation (4) and uses the technique of separation of variables, one can obtain
Figure 2. The motion of matter wave representing a massive particle appears as a vortex advancing in the direction k (which is parallel to the z-axis here).

Since we know now that ℓ is connected with the rest mass m through Equation (10), the above equation becomes

This is identical to the Klein-Gordon equation if we regard ψL as the particle wave function ϕ. This analysis suggests that the wave function described by the Klein-Gordon equation only represents the longitudinal component of the travelling wave of a free particle with a specific mass m. This means that the Klein-Gordon equation can only describe the movement of a particle along its trajectory. Its wave function does not give any information on the oscillation of the vacuum medium along the transverse plane.
Once the Klein-Gordon equation is derived, one can then obtain the Dirac equation to describe the motion of an electron by linearizing Equation (14) [19] . Furthermore, based on the Dirac equation, the Schrödinger equation can be derived under the condition when the Coulomb potential energy and kinetic energy are small in comparison to the rest mass of the particle. This derivation procedure had been shown elsewhere [20] .
Thus, our proposed basic wave equation is consistent with the commonly used quantum mechanical wave equations. The only difference is that the common quantum mechanical equations describe only the motion of a single type of particle. Furthermore, the wave functions in these quantum mechanical equations appear to describe only the motion of the excitation wave along the trajectory of the particle. The basic wave equation (Equation (4)), on the other hand, describes the complete wave function of the excitation wave of a free particle which may have different mass.
We may add that our discussion above only applies to the excitation wave of a free particle, such as a photon or an electron. For composite particles, such as protons or neutrons, the situation is much more complicated. One may need a further examination of the quark model. That will be far beyond the scope of this paper.
11. Conclusion
In conclusion, we believe all particles (with or without mass) are excitation waves of the vacuum medium. They behave like corpuscular objects only in the macroscopic view. Each of the particle properties and wave properties appears to have a one-to-one correspondence. Energy, momentum and mass are all related to the curvature of bending the vacuum medium during the propagation of the excitation wave. The similarity between the physical nature of energy and mass explains why the two can be converted between each other.
Acknowledgements
I thank the late Profs. John A. Wheeler and H. E. Rorschach for their encouragement when I started this work. I also thank Lan Fu for her assistance. The support of the Hong Kong University of Science and Technology to this work is acknowledged.
Cite this paper
Donald C.Chang, (2016) Why Energy and Mass Can Be Converted between Each Other? A New Perspective Based on a Matter Wave Model. Journal of Modern Physics,07,395-403. doi: 10.4236/jmp.2016.74040
References
- 1. Spergel, D.N. (2015) Science, 347, 1100-1102.
http://dx.doi.org/10.1126/science.aaa0980 - 2. Einstein, A. (1952) The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity. Dover Publications, New York.
- 3. Messiah, A. (1965) Quantum Mechanics. Wiley, New York.
- 4. Shankland, R. (1961) Atomic and Nuclear Physics. MacMillan, New York, 207.
http://dx.doi.org/10.1119/1.1937723 - 5. Kittel, C. (2005) Introduction to Solid State Physics. 8th Edition, John Wiley & Sons, Hoboken, NJ,.
- 6. Davisson, C.J. and Germer, L.H. (1927) Nature, 119, 558-560.
http://dx.doi.org/10.1038/119558a0 - 7. Halban, H.V.J. and Preiswerk, P. (1936) Comptes Rendus del’Académie des Sciences, 203, 73-75.
- 8. Estermann, I. and Stern, O. (1930) Zeitschrift Für Physik, 61, 95-125.
- 9. Chang, D.C. (2004) arXiv:physics/0404044 [physics.gen-ph].
- 10. Whittaker, E. (1951) A History of the Theories of Aether and Electricity. Thomas Nelson, London.
- 11. Michelson, A.A. and Morley, E.W. (1887) American Journal of Science, 34, 333-345.
http://dx.doi.org/10.2475/ajs.s3-34.203.333 - 12. Dirac, P.A.M. (1981) Chap. XI. Relativistic Theory of the Electron. In: The Principles of Quantum Mechanics, 4th Edition, Clarendon Press, Oxford, 253-275.
- 13. Kuhlmann, M. (2013) Scientific American, 309, 40-47.
http://dx.doi.org/10.1038/scientificamerican0813-40 - 14. Chang, D.C. (2013) Journal of Modern Physics, 4, 21-30.
http://dx.doi.org/10.4236/jmp.2013.411A004 - 15. Chang, D.C. and Lee, Y. (2015) Journal of Modern Physics, 6, 1058-1070.
http://dx.doi.org/10.4236/jmp.2015.68110 - 16. Longair, M.S. (1984) Chap. 3. The origin of Maxwell’s Equations and Their Experimental Validation. In: Theoretical Concepts in Physics, Cambridge University Press, Cambridge, New York, 40-49.
- 17. Klein, O. (1926) Zeitschrift Für Physik, 37, 895-906.
http://dx.doi.org/10.1007/BF01397481 - 18. Gordon, W. (1926) Zeitschrift Für Physik, 40, 117-133.
http://dx.doi.org/10.1007/BF01390840 - 19. Sakurai, J.J. (1973) Advanced Quantum Mechanics. Addison-Wesley, Reading, 75-89.
- 20. Cottingham, W.N. and Greenwood, D.A. (1998) An Introduction to the Standard Model of Particle Physics. Cambridge University Press, Cambridge, 72.




