Journal of Modern Physics
Vol.07 No.05(2016), Article ID:64071,13 pages
10.4236/jmp.2016.75046
Novel Bianchi VII Space Times and Their Properties
Manavendra Mahato, Ajay Pratap Singh
Discipline of Physics, Indian Institute of Technology Indore, Indore, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 December 2015; accepted 26 February 2016; published 29 February 2016
ABSTRACT
We construct and investigate non conformal anisotropic Bianchi type VII0 solutions in 5 dimensions. The solutions are asymptotically flat with a singularity. We also construct anisotropic solutions of Einstein-Maxwell gravity using a procedure similar to Majumdar-Papapetrou solutions with various profiles of charged dust and explore ways to hide the singularity behind the horizon. We further embed it in one higher dimension to get an asymptotically anti de Sitter space and approximate two point correlator of operators with higher conformal dimensions by calculating geodesic lengths. We find a peculiar power law decay of the correlator as a function of separation.
Keywords:
Bianchi Spacetimes, Anisotropic Spacetime, Gauge/Gravity Correspondence

1. Introduction
Inception of general relativity has led to great insights into cosmology as well as many open problems. General relativity encodes the interaction of matter or radiation with space time in a charming manner. Its various solutions have been studied in the past and many of them point to interesting properties about general relativity and cosmology. Among them, spherically symmetric solutions have received much attention so far because of their enhanced symmetries, simplicity and relevance in cosmology. However, many anisotropic solutions do exist in nature and such situations in general offer a far richer set of intricacies. Anisotropic, but homogenous solutions of Einstein equations were classified by Bianchi many decades ago. But, finding such solutions has always been challenging and has led to some results previously. Recently, anisotropic space times have gathered a renewed interest from a different direction. Many solutions of general relativity are much sought for the study of field theory using AdS/CFT correspondence as well as attractor mechanism [1] -[3] . Recently, asymptotic AdS (anti-de Sitter), anisotropic solutions were constructed and studied to investigate properties of certain anisotropic condensed matter systems using AdS/CFT correspondence. For example, see [4] -[15] .
In this context, asymptotically AdS, Bianchi VII class of solutions are also important as they were related using AdS/CFT correspondence to spatially modulated superconductors where the Cooper pair is not a s-wave, but a p-wave. The numerical solutions were constructed and their properties were further studied [16] -[19] . This motivated us to the idea that similar anisotropic solutions with asymptotically flat or de Sitter property can also be constructed. We take up the investigation of such solutions and their properties in this manuscript.
In this manuscript, we begin with constructing a simple, static but anisotropic solution of pure general relativity which is also asymptotically flat. Such simple cases usually lead to singular solutions. We report certain simple, analytic Bianchi VII0 solutions containing singularity. To address the problem of singularity, we include additional Maxwell and matter fields in one higher dimension and attempt to construct Majumdar-Papapetrou like solutions with anisotropic property preserved [20] -[23] . We seek to construct solutions with a regular horizon hiding any naked singularity and we report one such case, though it is sourced by a fictitious matter density.
We embark on a study to explore the effect of anisotropy in such spacetimes, their properties and dual field theories. We construct a 5 dimensional asymptotically locally anti de Sitter solution by adding a radial direction whose boundary metric is our anisotropic, 4 dimensional solution. Various foliations of such space away from the singularity can have well defined field theory on the boundary. Similar setups also provide a good platform to study the singularity and have inspired many to demystify cosmological singularities such as big bang. For example, see [24] -[30] . We use AdS/CFT correspondence to study two point correlators of higher dimensional operators living on the boundary. For such operators, the correlator gets most significant contribution from the length of the geodesics and this approach was recently used to study cosmological anisotropic singularites. We partially solve geodesic equations to evaluate the correlator and discuss its properties. Here the boundary is an anisotropically curved space which can impart peculiar properties to correlators.
2. Conventions and Notations
Three dimensional homogenous spaces have been classified by Bianchi into different classes [31] . Since homogenous spaces exhibit identical metric properties at all points in space, such spaces have translational symmetries. They contain 3 Killing vectors denoted here as
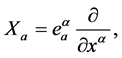 (1)
(1)
where 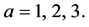 Due to lack of isotropy in general, these generators of translation are not always compatible with each other. Their Lie algebra can be represented as
Due to lack of isotropy in general, these generators of translation are not always compatible with each other. Their Lie algebra can be represented as
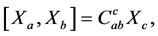 (2)
(2)
where 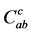 are called structure constants which are antisymmetric in lower indices,
are called structure constants which are antisymmetric in lower indices,
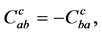 (3)
(3)
and they also satisfy Jacobi identity,
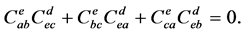 (4)
(4)
Taking into consideration the choices under scale transformation, local coordinate frame and signs, it was shown by Bianchi that there are 9 different possible classes. We hereby explicitly write the Killing vectors corresponding to Bianchi type VII,
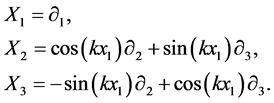 (5)
(5)
Here, k is a constant. It is usually fixed to be 1 by using diffeomorphism i.e. by reparameterizing kx to be new variable x and similar changes. We keep it explicit here by considering it as a small positive number. It is sometimes helpful to check the analogous isotropic case by taking the limit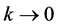 . The commutation relations between the generators can be checked to be non vanishing. The dual one forms of these vectors are
. The commutation relations between the generators can be checked to be non vanishing. The dual one forms of these vectors are
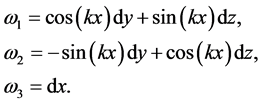 (6)
(6)
If the metric is to have Bianchi VII symmetry, then the one forms 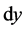 and
and 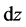 are restricted to appear in the above combinations only. We will use these one forms in subsequent sections to construct the metric ansatz.
are restricted to appear in the above combinations only. We will use these one forms in subsequent sections to construct the metric ansatz.
3. Anisotropic Solution of Pure Gravity Action
We attempt to construct here a simple anisotropic solution of pure gravity. For anisotropy, 3 spatial directions along the 3 non commutative Killing vectors are necessary. We add one extra radial direction r and make an ansatz that the metric coefficients of the various one forms are functions of r only. The action S for this section is
 (7)
(7)
Here, R is the Ricci scalar and g denotes determinant of the metric. The signature of our metric is chosen to be (+, +, +, +). We choose it to be all plus to keep the analysis simple. Our aim is to study unique properties due to anisotropy and an amenable choice of signs is desired. We will see later that time coordinate can be embedded in such spaces by introducing higher dimensions. We choose our ansatz for the metric to be
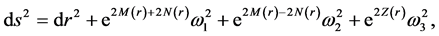 (8)
(8)
where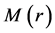 ,
, 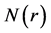 and
and 
Thus, we are looking for static, anisotropic Bianchi 
The Einstein equations of motion can be conveniently written in terms of a variable G which denotes




including a constraint which arises from (rr) component of Einstein equation,

Here, superscript prime denotes derivative with respect to r. The first equation suggests that a good radial variable will be u defined as

Such a choice simplifies the set of dynamical equations to

The constraint equation now becomes

We then proceed to express the function M as
where a and b are constants. The next amenable equation to solve is that for N. In general, this equation is non linear in u and requires numerical methods. However, it simplifies for a special case of

where 

which if integrated once, leads to

Here, 




Its general solution is

It can also be written as

The equation for Z can be written as

It has the general solution

Since 





This metric is Ricci flat, i.e. 



4. Anisotropic Solution of Einstein Maxwell Action
We now attempt to construct anisotropic solutions of 5 dimensional Einstein Maxwell action along with matter density. Our action in this section is

Here, notation g denotes the determinant of the metric which we choose to have one negative signature along time direction. Ricci scalar is denoted by R. The electromagnetic potential and field strength are denoted by 






The metric fluctuations of the action leads to following Einstein equations.
We further attempt to find solutions of these set of equations using a method employed earlier to find generalizations of Majumdar-Papapetrou metrics [22] [23] . We note that the Majumdar-Papapetrou metrics are 4 dimensional extremal solutions of Einstein-Maxwell equations of the type

along with an electromagnetic flux of the kind


The metric 

The indices 










We next evaluate the components of the Einstein tensor and they are found to be

We choose our internal subspace to be the anisotropic Ricci flat space that we obtained in last section i.e. Equation (25). Thus, Ricci tensor 


Next, we make an ansatz for the electromagnetic potential

We also make an ansatz for the four velocity of the matter density. We assume matter to be at rest i.e.

Such a choice also ensures that


The matter energy density contribution to energy momentum tensor is

The non trivial components of Einstein equations are
We notice that the term explicitly proportional to 

It can be solved easily if we take the function A proportional to function V. The equation fixes the relation to be

In terms of

We next make an ansatz for the source of the electromagnetic field. We take only the time component of 

This equation will be consistent with the Equation (40), if we choose

Thus we are left with a single equation viz. Equation (40), which is a non homogenous Laplacian equation. We now proceed to solve it for some suitable choices of matter density in the next section.
5. Anisotropic Solutions with Chosen Source Profiles
5.1. Polynomial Solutions
In the previous section, the Einstein equations were reduced to a single non-homogenous harmonic equation which is sourced by the density profile of the matter field. The equation now left to solve is

We choose our spatial subspace to be same as the anisotropic 4 dimensional subspace which was obtained in the section (3). Therefore,

The determinant of the metric is



We next define polar coordinates 


where we have taken 


where, n is a positive integer greater than 2 and c is a constant. Such a form of energy density is physically reasonable as it vanishes smoothly to zero when one proceeds towards infinity. Then Equation (46) becomes,

One can easily solve it to obtain

We can restrict ourselves to polynomial form by choosing

We further proceed by making a particular choice of

Then, the metric now appears as

But, this solution shows two essential singularity where Kretschmann tensor diverges. They are 





We find that the (tt) component of the metric for small values of r is

Thus, this solution has a horizon near

5.2. Sine Gordon Solution
One can get here an equation of Sine Gordon type by a different choice of matter density. First, we choose a different radial coordinate
Then the Equation (46) becomes

Next, we choose matter density profile to be of form

The above equation then reduces to a Sine Gordon equation,

It admits a solution

The resultant metric looks like

The range for coordinate r is restricted from 



6. Asymptotically Anti de Sitter Space
We further explore the properties of the Ricci flat 4 dimensional metric obtained in section (3). We consider a massive (but not back-reacting) field living in this space. Recent advances in gauge/gravity correspondence allows us to approximate its two point correlations for strong self coupling of the field. The correspondence states that the generating functional of the correlations of a 4 dimensional strongly coupled field theory defined on the boundary of a 5 dimensional asymptotically anti de Sitter space is same as the partition function of the latter theory of gravity. The boundary values of fields in the gravitational theory are coupled to sources of appropriate fields in field theory [32] -[35] . The method to calculate correlator in our 4 dimensional space will be to embed it in an anti de Sitter (AdS) space with one higher dimension such that it behaves as its boundary. The two point correlator of the massive field can be related to geodesics traveling in higher dimensional AdS space. We expect that these correlators will capture the effect of singularity in the same way as cosmological singularities are demonstrated to show such behavior in similar setups [24] -[30] . The embedding for our case is

We note that the above metric is an Einstein metric and its curvature invariants are
Thus, the metric shows a singularity at


with the following curvature properties.

This is Euclidean anti de Sitter space and it can be verified that the metric in Equation (61) is the same as AdS in Poincare coordinates after a change of variables. [Take

Since the metric asymptotically becomes Euclidean anti de Sitter, it can be conjectured along the lines of AdS/CFT duality that it can be explored to learn about an Euclidean Yang Mills theory living in an anisotropic background in its strong coupling limit. Simplest quantity that can be calculated to probe the field theory is the two point correlation function for operators with high conformal dimensions. This correlation can be approximately given in terms of the length of the geodesics with endpoints on the boundary [24] .
We next calculate the geodesics connecting two endpoints on the boundary 

where 
Here, 

If we write this expression explicitly in terms of constant of motion X, we get
Similarly, one can obtain another constant of motion Y as
Simplifying the above two equations leads to

If we denote the expression
then the remaining geodesic equations can be written as

With a little manipulation, we can find a conserved quantity along the geodesic as

This constraint considerably simplifies the dynamical equation for variable t, which can now be solved to obtain

where D is another integration constant. We note that t becomes zero for both


The maximum value of the scale invariant quantity 

length of the geodesic. To deal with divergences, we put a cutoff for the affine parameter. We choose it to vary between 










Using the identity Equation (67), we simplify it to

The latter part can be identified as the divergent contribution due to asymptotic AdS geometry and can be dropped during regularization. We next calculate the length of the geodesic on the boundary by using the boundary metric.
Thus, 


Thus, the two point correlators for higher dimensional operators living on the boundary metric is expected to show a behavior [24]

Here the mass of the field (m) is also approximated to be same as conformal dimension (


7. Conclusion
We have constructed an anisotropic 4 dimensional asymptotically flat Riemannian metric which is also Ricci flat. We later incorporated it in a 5 dimensional space time along with matter density and electromagnetic flux using a method similar to Majumdar-Papapetrou way of constructing extremal solutions. With certain choices of matter density profiles, we were able to construct explicit solutions. The singularity problem seems to be addressed for a case of a fictitious choice of matter density for which we arrived at a solution with a horizon hiding the singularity. Using our method, interesting anisotropic solutions in higher dimensions can be constructed by further investigating different types of Lagrangians for their properties. Given the importance of anisotropic Bianchi VII space-times for their relations with condensed matter systems, we proceeded to study their properties. We embedded the metric in 5 dimensions analogous to the flat space embedding in anti de Sitter space manifested in the Poincare metric. Apart from the 3 directions along the 3 non commutative Killing vectors, we have 2 other spatial directions; one, the u-direction along which the metric coefficients vary. The other is the radial direction towards the bulk of the AdS space. The subspace for a fixed u and its neighbourhood can be considered locally AdS where the bulk metric encodes the properties of the field theory lying on its boundary, which is itself anisotropic. We examined the effect of anisotropy on the properties of the quantum field theory on such background by approximating the two point correlator of two operators with high conformal dimensions. For small separation between the operator positions, we saw a dependence similar to a conformal theory living on the flat space. The effect of curvature of the background is not reflected in this case. However for large separations, the two point correlator vanishes as a power law of the separation between the operator positions. We expect that the large distance behavior is unique to our case and encodes the effect of singularity into it.
Acknowledgements
The authors acknowledge the financial support of DST grant number SR/FTP/PS-149/2011.
Cite this paper
ManavendraMahato,Ajay PratapSingh, (2016) Novel Bianchi VII Space Times and Their Properties. Journal of Modern Physics,07,445-457. doi: 10.4236/jmp.2016.75046
References
- 1. Iizuka, N., Kachru, S., Kundu, N., Narayan, P., Sircar, N. and Trivedi, S.P. (2012) Journal of High Energy Physics, 1207, 193.
http://dx.doi.org/10.1007/JHEP07(2012)193 - 2. Iizuka, N., Kachru, S., Kundu, N., Narayan, P., Sircar, N., Trivedi, S.P. and Wang, H. (2013) Journal of High Energy Physics, 1303, 126.
http://dx.doi.org/10.1007/JHEP03(2013)126 - 3. Kachru, S., Kundu, N., Saha, A., Samanta, R. and Trivedi, S.P. (2014) Journal of High Energy Physics, 1403, 074.
- 4. Kachru, S., Liu, X. and Mulligan, M. (2008) Physical Review D, 78, Article ID: 106005.
http://dx.doi.org/10.1103/PhysRevD.78.106005 - 5. Son, D.T. (2008) Physical Review D, 78, Article ID: 046003.
http://dx.doi.org/10.1103/PhysRevD.78.046003 - 6. Balasubramanian, K. and McGreevy, J. (2008) Physical Review Letters, 101, Article ID: 061601.
http://dx.doi.org/10.1103/PhysRevLett.101.061601 - 7. Danielsson, U.H. and Thorlacius, L. (2009) Journal of High Energy Physics, 0903, 070.
- 8. Hartnoll, S.A., Polchinski, J., Silverstein, E. and Tong, D. (2010) Journal of High Energy Physics, 1004, 120.
http://dx.doi.org/10.1007/JHEP04(2010)120 - 9. Balasubramanian, K. and Narayan, K. (2010) Journal of High Energy Physics, 1008, 014.
- 10. Donos, A. and Gauntlett, J.P. (2010) Journal of High Energy Physics, 1012, 002.
- 11. Singh, H. (2010) Journal of High Energy Physics, 1012, 061.
- 12. Gregory, R., Parameswaran, S.L., Tasinato, G. and Zavala, I. (2010) Journal of High Energy Physics, 1012, 047.
- 13. Cassani, D. and Faedo, A.F. (2011) Journal of High Energy Physics, 1105, 013.
- 14. Lu, H., Pang, Y., Pope, C.N. and Vazquez-Poritz, J.F. (2012) Physical Review D, 86, Article ID: 044011.
http://dx.doi.org/10.1103/PhysRevD.86.044011 - 15. Shu, F.W., Lin, K., Wang, A. and Wu, Q. (2014) Journal of High Energy Physics, 1404, 056.
- 16. Nakamura, S., Ooguri, H. and Park, C.S. (2010) Physical Review D, 81, Article ID: 044018.
http://dx.doi.org/10.1103/PhysRevD.81.044018 - 17. Ooguri, H. and Park, C.S. (2010) Physical Review D, 82, Article ID: 126001.
http://dx.doi.org/10.1103/PhysRevD.82.126001 - 18. Donos, A. and Gauntlett, J.P. (2012) Physical Review Letters, 108, Article ID: 211601.
http://dx.doi.org/10.1103/PhysRevLett.108.211601 - 19. Donos, A. and Gauntlett, J.P. (2012) Physical Review D, 86, Article ID: 064010.
http://dx.doi.org/10.1103/PhysRevD.86.064010 - 20. Myers, R.C. (1987) Physical Review D, 35, Article ID: 455.
http://dx.doi.org/10.1103/PhysRevD.35.455 - 21. Gibbons, G.W. and Warnick, C.M. (2009) Physical Review D, 79, Article ID: 064031.
http://dx.doi.org/10.1103/PhysRevD.79.064031 - 22. Varela, V. (2003) General Relativity and Gravitation, 35, Article ID: 1815.
http://dx.doi.org/10.1023/A:1026014114308 - 23. Frolov, V.P. and Zelnikov, A. (2012) Physical Review D, 85, Article ID: 064032.
http://dx.doi.org/10.1103/PhysRevD.85.064032 - 24. Hertog, T. and Horowitz, G.T. (2004) Journal of High Energy Physics, 0407, 073
http://dx.doi.org/10.1088/1126-6708/2004/07/073 - 25. Hertog, T. and Horowitz, G.T. (2005) Journal of High Energy Physics, 0504, 005
- 26. Awad, A., Das, S.R., Nampuri, S., Narayan, K. and Trivedi, S.P. (2009) Physical Review D, 79, Article ID: 046004.
http://dx.doi.org/10.1103/PhysRevD.79.046004 - 27. Fischetti, S., Kastor, D. and Traschen, J. (2014) Classical and Quantum Gravity, 31, Article ID: 235007
http://dx.doi.org/10.1088/0264-9381/31/23/235007 - 28. Engelhardt, N., Hertog, T. and Horowitz, G.T. (2014) Physical Review Letters, 113, Article ID: 121602
http://dx.doi.org/10.1103/PhysRevLett.113.121602 - 29. Engelhardt, N., Hertog, T. and Horowitz, G.T. (2015) Journal of High Energy Physics, 1507, 044.
http://dx.doi.org/10.1007/JHEP07(2015)044 - 30. Banerjee, S., Bhowmick, S., Chatterjee, S. and Mukherji, S. (2015) Journal of High Energy Physics, 1506, 043.
http://dx.doi.org/10.1007/JHEP06(2015)043 - 31. Landau, L.D. and Lifshitz, E.M. (1975) The Classical Theory of Fields. Vol. 2, 4th Edition, Butterworth-Heinemann, Oxford.
- 32. Maldacena, J.M. (1999) International Journal of Theoretical Physics, 38, 1113. [(1998) Advances in Theoretical and Mathematical Physics, 2, 231].
http://dx.doi.org/10.1023/A:1026654312961 - 33. Witten, E. (1998) Advances in Theoretical and Mathematical Physics, 2, 253.
- 34. Gubser, S.S., Klebanov, I.R. and Polyakov, A.M. (1998) Physics Letters B, 428, 105.
http://dx.doi.org/10.1016/S0370-2693(98)00377-3 - 35. Freedman, D.Z., Mathur, S.D., Matusis, A. and Rastelli, L. (1999) Nuclear Physics B, 546, 96.
http://dx.doi.org/10.1016/S0550-3213(99)00053-X
1For positive sign in Equation (20), one needs 















