Journal of Modern Physics
Vol.06 No.11(2015), Article ID:59624,13 pages
10.4236/jmp.2015.611152
On an Intriguing Invention Albert Einstein Made Which Has Gone Unnoticed Hitherto
Jean-Paul Auffray
ex: Courant Institute of Mathematical Sciences, New York University, New York, USA
Email: jpauffray@yahoo.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 August 2015; accepted 13 September 2015; published 16 September 2015
ABSTRACT
We retrieve three mysterious sentences Albert Einstein wrote in the early years of his wondrous scientific career. We examine their implications and we suggest that they provide a surprising new basis for Quantum Physics as well as some enlightenment concerning the whereabouts of Dark energy.
Keywords:
Einstein, Absolute Measurements, Electromagnetic Energy, m = E/c2, Space Points, Dark Energy, M. S. El Naschie, Quantum Meteorites

1. Introduction
Einstein’s name is affixed to stunning discoveries made in the field of theoretical physics in the early years of the twentieth century. Less known is the fact that, even as he worked then as a Technical assistant Third Class in the Swiss Patent Office in Bern, Einstein also made a genuine great invention (i.e. discovered a hidden treasury, as in archeology) which has remained unnoticed hitherto. We retrieve this invention in the present note and we examine what it entails. Three mysterious sentences that Einstein wrote at that time will help us in this endeavor.
2. The Circumstances
Unemployed and penniless in the early years of the Twentieth century, young Einstein took refuge in his father’s house on Via Bigli in the industrious city of Milan (Milano) which had been at the heart of the rebellion against Austrian domination half a century earlier and where the Kingdom of Sardinia had been founded, which soon gained control of most of Italy and in 1861 had been rechristened the Kingdom of Italy. Seeing his son in distress, Hermann Einstein daringly sent a letter to a university professor who was then “the” towering figure in German science, Wilhelm Ostwald, telling him: “My son feels profoundly unhappy with his present lack of position, and his idea that he has gone off the tracks with his career & is now out of touch gets more and more entrenched each day.” He justified his selection of this particular correspondent, assuring him (official translation, our emphasis: “It is you, highly honored Herr Professor, whom my son seems to admire and esteem more than any other scholar currently active in physics” [1] . On March 19th a few weeks later, young Albert himself addressed to the same professor a letter which contains a mysterious sentence which reads (official translation, our emphasis): “Esteemed Herr Professor! […] Permit me also to inquire whether you might have me for a mathematical physicist familiar with absolute measurements […]” [1] .
Familiar with absolute measurements… We will return to this statement in a moment.
3. Meanwhile in the Netherlands
Even as Einstein in Milan strived to build a future for himself, on December 11th 1900, which happened to have been a Tuesday, the University of Leiden (Universiteit Leiden, Figure 1) in the Netherlands presented to its illustrious professor of theoretical physics, the Dutch physicist Hendrik Antoon Lorentz, a collection of essays (a Festschrift) that his colleague physicists and mathematicians in Europe and America had written (secretly) in his honor to celebrate the 25th anniversary of his doctorate. One of the most remarkable essays in this presentation was the paper that a mining engineer who happened to be also a genius mathematician had contributed to the Festschrift under the title “The Theory of Lorentz and the Principle of Reaction” [2] . This paper is fascinating to read a century later because it is essentially dedicated to the presentation by its author of a fundamental discovery that he (not Lorentz) had made some years earlier―he had mentioned it casually in one of his professorial lectures at the University of Paris, the famous Sorbonne. He presented it in his Festschrift paper in these terms: “If any sort of device produces electromagnetic energy and radiates it in a particular direction, that device must recoil just as a cannon does when it fires a projectile”. He then asserted: “It is easy to evaluate that recoil quantitatively” and he gave a numerical example which translates directly to this relation:
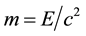 (1)
(1)
attributing an “electromagnetic mass” m (a new concept) to an “electromagnetic bullet” (also a new concept) transporting a pulse of “electromagnetic energy” E at the speed of light c. Written as E = mc2, this relation has become known since around the world as “the most famous equation in the history of physics”.
This communication deprived Einstein of the opportunity to have been the first in modern times to formulate the famous equation. But he had an excuse: as we have just seen: in 1900, penniless and unemployed he had not yet begun his scientific career; he had not been and could not have been invited to contribute to the Leiden Festschrift.
4. Strictly Speaking
Strictly speaking, as constructed by its inventor in 1900, Equation (1) applies only―strictly speaking―to electromagnetic energy, i.e. to energy carried by electromagnetic waves―light. Does it also apply to other forms of energy? In particular does it also apply to the so-called Dark energy physicists have worried about for the past several decades?
In calculations we reported recently [3] , the System of the World contains two kinds or species of points: i-points which form a substrate in the frame of which they bear no (geometric) relations of distance or proximity with each other; and e-points (endpoints) which form a structure having characteristics that Isaac Newton once attributed to Absolute space. When one of these points is randomly set in motion, it acquires a momentum p
Figure 1. Universiteit Leiden welcome motif. http://www.leiden.edu/uploads/homepage/hp14.jpg Welcome motif of the Dutch university where the (modern) discovery of m = E/c2 (E = mc2) was announced in print for the first time.
and a space length l thereby becoming a quantum meteorite which transports a pulse of electromagnetic energy E for a time lapse duration d. The four parameters l, p, E and d are subjected to a constraint, the Absolute Certainty Principle (ACP), a law of nature which requires that, taken together, the four parameters l, p, E and d must satisfy with absolute certainty the fundamental relation
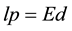 (2)
(2)
which makes the composite Ed a sort of “echo” of the composite lp. What we alluded to in [3] , but did not develop fully then, is the fact that the impact of the ACP on the meteorite involved depends on whether the point concerned was at the origin a i-point or a e-point.
5. E-Quantum Meteorites
E-points by definition are “endpoints”. As a reminder, this arises as follows.
Consider the Unit Line Segment (ULS)

“Evaporate” or “sublimate” all the points the segment contains with the exception of its two endpoints marked e0 and e1 on the above diagram, an intervention we have baptized a surreptitious quantum little bang. Left behind after the line segment deconstruction has been completed, these two endpoints become e-points compelled to maintain relations of order, whatever that might mean, with each other as well as with the other e-points present in the structure. This constraint prevents somehow the e-point which has been randomly set in motion from behaving quite as freely as i-points quantum meteorites do.
In String theory, when an open string propagates through space-time, its endpoints are required to lie on a D-brane, the letter “D” referring to the “Dirichlet boundary condition”. To discover how the constraint might intervene in our case, let us review succinctly how Equation (2) can be derived.
It is properly be written as
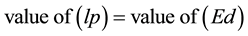
Thus written, it tells us that the composite Ed, which involves energy and time, is some sort of a replicate, ricochet or “echo” of the composite lp, which refers to space and motion. This is a result of considerable significance. To appraise it at its proper level, let us look as we did in [3] into the Alchemist Magician Hat under the scrutiny of the Great Alchemist himself, Isaac Newton.
6. Found in Newton’s Alchemist Hat
In [3] we searched in the Newton Alchemist Hat and we made an “invention” (i.e. the discovery of a hidden treasury). We found in the Hat a treasure that physicists had long believed had been lost forever, Absolute Space. We retrieved Absolute Space and in the now empty Hat (we thought) we found an additional treasure: a point- like object possessing strange characteristics which had escaped attention hitherto. Examining it at close range, we found it to be under the permanent control of an unsuspected law of nature, the Absolute Certainty Principle, which requires said point-like object to follow with absolute certainty paths in Absolute space according to the relation
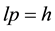
in which h is the famous “Planck constant” and the word paths refers to Feynman paths in action, not to trajectories in space and/or time. But no trace in the Hat of Newton’s Absolute Time.
We pondered why. And suddenly a word we used casually above surged in our mind as containing―per- haps―at least an element of the answer: we remarked an instant ago that the composite Ed is a sort of replicate or echo of the composite lp.
We submit that, at least in certain circumstances, time is a distorted view of space, or more precisely that a time lapse duration d is an “echo” of a space length l. This means that there must exist a relation connecting l and d… at least in the particular case of e-quantum meteorites.
Let us attempt to find what that relation might be.
7. Swept under the Rug (i.e. under the Carpet)
If it does not fit in your scheme, they say, sweep it under the rug―扫到地毯下 in Chinese. If you feel curious, look under the rug, you might find something there that famous people―say Einstein―have swept under the rug because it did not fit in their schemes.
We felt curious and we looked under the rug. We found under the rug a small piece of paper on which someone―Einstein?―had written some kind of an equation―in fact not an equation at all, simply the Greek letter “β” written in italics: β. We laughed.
Not for long.
Einstein describing himself in 1901 as “a mathematical physicist familiar with absolute measurements” (see our Heading 2) started us thinking: if Ed is to be an “echo” of lp, we thought, and more precisely if d is to be a “distorted representation” of l, then let us assume quite simply that l and d are related (are connected) to each other by a proportionality constant. Call it c. then
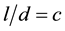
and we see that, measuring the ratio between a space length l and a time lapse duration d, our “absolute measurement” proportionality constant c has the dimension of… a velocity or speed―why not the “speed of light” which has preoccupied natural philosophers and “physicists” after them ever since the day when young Danish astronomer Ole Christensen Rømer or Römer, then working at the Observatoire Royal in Paris, determined in 1676 that it has a finite (constant) value, which, understood as an absolute measurement, makes one second of time correspond to a space length of 299,792,458 meters by today’s reckoning―this fits perfectly well with our scheme.
We are thus led to a (first) conclusion: a e-point in motion is a e-quantum meteorite which moves at the so- called speed of light. Our fundamental scheme for e-quantum meteorites set in motion can then be written on the back of an envelope:

yielding
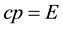
a classical result… which relates of course to the relation m = E/c2 referred to in our Heading 3: it tells us that an electromagnetic “bullet”―a e-quantum meteorite in our terminology―which carries a pulse of electromagnetic energy E at the speed of light also carries with it an electromagnetic momentum p and therefore an electromagnetic mass m related to it by the relation cp = c∙mc = mc2 = E. The novelty is that this result arises from a suspected “constraint” affecting e-points “localized” in the Absolute space structure of the System of the World.
Very well, but why does the constraint yield for c the particular value c = 299,792,458 m/s as experimentally determined?
In geometry, the circumference of a circle of radius r is equal to 2πr, with the proportionality constant π having the particular value
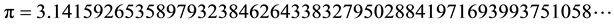
Why this particular value?
We do not know.
Let us return to the Great Invention that Einstein made which has gone unnoticed hitherto. He made it while being caught in the Great Game of Dupes (GGD).
8. The Great Games of Dupes
8.1. Identifying Unidentified Drifting Objects
At the annual meeting of the British Association for the Advancement of Science held in Belfast in August 1874, George Johnstone Stoney, then the good-natured (and elegantly-bearded) Secretary of the Queen’s University of Ireland in Dublin, made science history as he declared: “Nature presents us, in the phenomenon of electrolysis, with a single definite quantity of electricity which is independent of the particular bodies acted on” [4] .
A single definite quantity… we would say today, a quantum.
He then proposed: “This definite quantity of electricity I shall call Er”, adding daringly: “If we make this our unit quantity of electricity, we shall probably have made a very important step in our study of molecular phenomena.”
8.2. Looking for Physical Units of Nature
Shortly after this announcement, George Stoney published a paper “On the Physical Units of Nature” in which he called attention to his minimum quantity of electricity Er as being one of three physical units, “the absolute amounts of which are furnished to us by Nature” to which he added “which may therefore be made the basis of a complete body of systematic units in which there shall be nothing arbitrary” [5] .
Stoney’s other two physical units were the “Maxwell” of velocity―to us today the velocity or speed of light in vacuum―and the “Newton” of gravitation (even though Newton never used such a unit in his investigations).
With his stunning 1874 declarations, Stoney had unwillingly opened the door to an incandescent stream of uncontrolled thoughts which, a quarter of a century later, would lead astray the newly conceived Quantum Physics―as we shall presently discover.
8.3. Inventing a System of Units for All Times and All Civilizations
In 1865, German physicist Rudolph Clausius, then forty-three-years old, had a preference for letters from the last half of the alphabet to represent entities in his equations―he used the letters M to Z, except O and Y. He selected the letter S to represent a concept he had just invented. As for a name, he elected the prefix “en” and the suffix “-ie” used in the name “Energie” and appended in-between the word “trop”, from the Greek “trope” meaning “transformation”. Thus was born the (German) word “Entropie”―Entropy in English to us today.
Thirty-four years later, on Thursday May 18th 1899, then in his forty’s and at the peak of his creativeness, Berlin theoretical physicist Max Planck decided to trace his own pathway in the giant footsteps his great predecessors Rudoplh Clausius and George Stoney had implanted in the fertile soil of physics invention in 1865 and 1874. A deep believer in the thermodynamic concept of Entropy, he read a report to the newly formed German Physical Society (the Deutsche Physikalische Gesellschaft) self-proclaiming his recently formulated logarithmic law of entropy to be a “Universal law of nature”. Then―consciously or unconsciously borrowing the idea from Stoney―he announced that he had carried out the strenuous task of constructing a “Natural system of units” assigning units to all the physical entities known in his days in the form of functions of four “universal constants” of his invention―four, where Stoney had believed that three would suffice.
In embarking on this ambitious project Planck had in mind a plan even more grandiose than the plan Stoney had imagined in 1874: These units, said Planck, “ will necessarily maintain their significance for all times and all civilizations, including extra-terrestrial and non-humans and hence can be designated as “Naturconstanten” (Nature Constants).
Clausius had used capital letters from the second half of the alphabet to designate terms in his equations, to represent his “Nature constants”, Planck used lower case letters taken in the first half of the alphabet: a, b, c and f. These units are known today under modernized symbols and names (suggested by Planck himself on second thoughts):
a has become k and is known as the Boltzmann constant (even though Planck, not Boltzmann, invented it).
b has become h and is known as the Planck constant.
c has remained c and is known as measuring the speed of light (in vacuum).
F has become G and is known as the Newton gravitational constant (even though Newton never used it in his calculations) [6] .
9. The Equation of Happiness
In 1894, the Leipzig professor whom Hermann Einstein had contacted in 1901 telling him “It is you, highly honored Herr Professor, whom my son seems to admire and esteem more than any other scholar currently active in physics” had gone in semiretirement, living with his family in his estate the “Landhaus Energie”―the Country house of Energy―in the small town of Großbothen in Saxony. Now free of his responsibilities as a professor at the University of Leipzig, he participated actively in Germany’s “Monistic movement”, challenging the Church with “Sunday sermons” and promoting the unified science of nature he called Energetics, a generalized form of thermodynamics. One of his ambitions was to replace Planck’s System of Units destined to remain valid for All Times and All Civilizations by his own system making space, time and energy the fundamental entities of nature, supported by Absolute measurements.
In 1905, this now fully-retired professor published as part of his theory of Energetics, a “Theory of Happiness” based notably on a “Happiness equation” which reads [7]

where G stands for Gluck (happiness), A for Arbeit (energy expended in doing useful work), W for Widerstand (energy dissipated in overcoming resistance) and where k is an ad hoc adjustable proportionality constant.
10. Playing the Great Games of Dupes
10.1. Playing Allotria
In 1905, which was to become his famous Annus Mirabilis, Einstein was in a new kind of trouble. Not financially; he was now in his third year working full time as a technical assistant (Examiner) level III, the lowest―as a “cobbler” he said―in the Swiss Patent Office in Bern, a very demanding job that he had been able to secure thanks to the backstage intervention of his best friend’s father, Jules Grossmann. Founded in 1888 and officially named l’Institut Fédéral de la Propriété Intellectuelle (IPI) in French, Eidgenössisches Institutfür Geistiges Eigentum (IGE) in Einstein’s mother tongue (German), Istituto Federaledella Proprietà Intellettuale in Italian, the Swiss Federal Institute of Intellectual Property―the “Patent Office” for short―received day after day written requests for the attribution of a patent―recognition of intellectual property rights―for the invention of new gadgets (devices) described in the submitted document(s). The Office Director gives the document(s) to one of his Examiners; taking into account his field of expertise―the theory of Heat and electrical devices, in the case of Einstein. Standing eight hours a day at a lectern, the selected Examiner is required to study (examine) the document(s) and write a report “in clear and understandable language” to help the Office decide whether the submitted invention actually works, is deserving of patent protection or whether it infringes on existing patents and should be denied the grant of the protection. This tedious occupation has prevented young Einstein so far to make a name for himself in his (secret) field of predilection, Absolute Measurements.
To survive in this tedious environment―and to keep his job―Einstein, now a married man and the proud father of a son, had wisely set up a strict discipline for himself; he reportedly divided his days in three segments of equal lengths: eight hours working at his “cobbler’s trade” at the Patent Office; eight hours sleeping; and eight hours devoted to “Allotria”―a German word derived from the ancient Greek ἀλλότριος (allótrios) from ἄλλος, “other”, the translations of which correspond precisely to what his boss forbade him to do while working at the Office: engage in monkey business, fool around, lark about, mess around in English [8] … He pursued his own search of happiness following two parallel courses:
1) A passive course: reading.
2) An active course: writing.
10.2. Reading
1) At the Swiss Patent Office in 1905, Einstein read―examined―day after day dozens, perhaps hundreds of patent applications.
2) At home or with friends after hours, he read―examined―dozens, perhaps hundreds of physics papers published in the major journals at that time―Annalen der Physik in Germany; Il Nuovo Cimento in Italy; Philosophical Magazine and Journal of Science in Great Britain; Comptes Rendus in France; and even some esoteric journals such as Finska Vetenskaps-Societeten. Öfversigtaf Förhandlingar. You had to be a Cobbler to be aware of its very existence.
How do we know this? Einstein himself told us so (implicitly, see below).
10.3. Writing
1) Having read―examined―a patent application, Einstein writes a report concerning it, long-hand, presumably using one of the two fountain pens he owned at that time [9] and he presents it to the Office Director.
2) At home later in the day, in the company of his wife and/or friends, he writes either a recension―a “review”―of one of the published physics papers he and/or one of his science-minded friends has read― retrieved―in one of the journals referred to above and found interesting―intriguing? To allude to what happens next we have no choice but to divulge here a hitherto well-kept secret. By 1905 Einstein had established a private understanding with a mysterious influential “correspondent” in Berlin. He sends the recension―the review―to this correspondent in Berlin, who has it published without further ado in the Beiblätter zu den Annalen der Physik, the monthly Supplement to Annalen der Physik. In 1905 alone, the Beiblätter published twenty-one of Zinstein’s recensions. As for the major papers hr wrote and published that year in Annalen der Physik…
If his correspondent―if his accomplice in Berlin―had not existed, in all likelihood Einstein would have remained “Herr Einstein”, a middle-class ordinary citizen employee in the Patent Office in Bern and he would not have become Einstein, the genial inventor of E = mc2 and of the theorie(s) of Relativity. Instead…
10.4. Einstein Writes His Heuristic Paper
Einstein’s Annus mirabilis began outwardly in the second half of March 1905 after he had sent to his correspondent in Berlin a flurry of six reviews of papers dealing with the theory of Heat (Thermodynamics), his official field of expertise at the time. He had selected the papers to review in five different European scientific journals. Leaving these reviews aside, let us concentrate our attention on the first of the five papers he sent to Berlin for publication in Annalen der Physik that year. Titled “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt” in German, it has become commonly known in English-speaking countries as Einstein’s “Heuristic paper”.
From the Ancient Greek Εὑρίσκω, “find” or “discover”, the qualifier “heuristic” is interesting―intriguing― but it would take us too far astray to try to unravel the mystery.
Einstein sent the paper out to Berlin on March 17th 1905; it was received by his correspondent the next day and it appeared in print in Annalen der Physik as the 14th paper proposed in the June 9th 1905 issue of the journal [10] .
The Heuristic paper covers seventeen pages. In it, Einstein uses the word Energie―by itself or in combinations German-style as in Energieelement―sixty-six times. Remarkably, the expressions “elementary quantum of action” or “Planck constant” and the symbol h which represents them in equations do not appear in the paper― not even once! And this is not an accident. A careful reading of the paper, either in the German original or in one of its “official” translations, shows clearly that this omission was Einstein’s deliberate choice. In view of the impact Einstein had on Quantum Physics in the early stages of its development, let us review (succinctly) how Einstein performed this acrobatic deed―without a net to protect himself in case of fall!
10.5. Einstein Makes the Planck Constant Disappear in Thin Air: A Perilous Exercise
The Heuristic paper deals primarily―to a large extent―with the problems raised in the consideration of the “black-body radiation”. The so-called “black-body”―in reality an “oven” which is “all-white” inside and has a small hole on its side through which radiation can escape―emits radiation (through this hole) with an intensity which is a function I (T, ν) of the body’s absolute temperature T and the frequency ν for which the intensity is measured. To perfect his history-making formula accounting for this function, Berlin genius physicist Max Planck, in 1900, needed an exponential factor e−x with x a pure number of course. In a desperation move [11] he expressed this pure number as the ratio hν/kT of two factors, hν and kT, having both the dimension of an energy, with k and h two “universal constants”. He then constructed the famous formula that every physicist in the world has seen at least once in his life. In it the exponential factor appears as
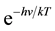
Einstein once remarked: “The secret of creativity is knowing how to hide your sources” [12] . If he had reproduced this factor in his Heuristic paper exactly as Planck had written it in 1900, Planck’s symbol h would have appeared in the paper―an undesirable feature by Einstein’s “creativity” requirement quoted above. Einstein made it disappear.
But you had to be an astute observer of human nature―you had to be Einstein―to imagine a trick that would go undetected.
There is a nice French expression which applies here: Ni vu ni connu… Noch gezien, noch bekend… in Dutch, Weder gesehen noch bekannter… in German, 没有见过, 也没有已知的 in Chinese. Neither seen nor known… in English. To prevent the troublesome symbol h from appearing in his paper, the Cobbler, as he once called himself, simply wrote the exponent of the exponential factor as −βν/T instead of hν/kT as it appeared in Planck’s original formula. And he gave no explanation or introduced, defined or justified his use of the (hitherto unknown) symbol β. It just appeared there―ni vu ni connu…
We had noticed the substitution some time ago… but we paid no attention to it―a detail. A detail which made it possible for Einstein to fulfill in his paper No. 6 his secret ambition: to place Energy instead of dynamical Action (h) at the core of the then emerging Quantum Physics. And just in case one has a doubt…
10.6. Let Us Be Sherlock Holmes
Einstein introduced his new “constant” β without giving any information to his readers as to its significance, satisfied to provide a numerical value for it in Section 2 of his paper, where he writes: β = 4.866 × 10−11 with no indications of units as if his “constant” was a pure number, which it is not. Let us be Sherlock Holmes and investigate what the dimensions of the mysterious “Einstein constant” β might be―after all we know the “Planck constant” h to have the dimension of dynamical action, and that does not disturb anyone; most physicists simply ignore this disturbing fact and treat h any odd way as they would any regular constant such as π, for instance, discarding happily the disastrous consequences that this treatment entails in the case of h..
The Einstein constant measures the ratio h/k of the Planck constant h and the Boltzmann constant k, which are two pillars of the Planck Universal System of units. This “ratio” is easily taken: h has the dimension of an energy “multiplied” by a time, while k has the dimension of an “energy per (degree) Kelvin”. The outcome of this back-of-an-envelope calculation is straightforward… and amazing: The Einstein constant β measures an entity which has the strange dimension of a “time duration per (degree) Kelvin”:
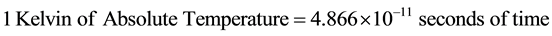
whatever that might mean physically. Einstein did not say.
All of this quite naturally rings a bell.
11. Are Einstein’s Energy Quant-Meteons?
In our preceding communication [3] we coined the expression “quantum meteorites” to designate “points in motion”. To simplify writing in what follows we shall replace it by the shorter expression “meteons”.
The concept of point [Punkte] or of space point [Raumpunkte] is fundamental to Einstein in his Heuristic paper even though he never goes beyond using the words without ever “defining” their physical meaning. This is particularly evident when he speaks of “a light ray starting from a point” [von einem Punkteausgehenden Lichtstrahles] or of electrons “which are bound to points in space” [Raumpunktegeketteten Elektronen].
In the first of the two sentences that interest us here Einstein describes in simple terms his Allotria invention of the concept we call today the photon: “According to the assumption considered here, he wrote, when a light ray starting from a point is propagated, the energy is not continuously distributed over an ever increasing volume, but it consists of a finite number of energy quanta, localized in space, which move without being divided and which can be absorbed or emitted only as a whole.”
We do not feel being particularly adventurous in identifying Einstein’s Energiequanten, which are “points” (Punkte) which “move without being divided”, with our e-quantum meteorites (e-meteons) which are also points which move without being divided. This impression is comforted when we read Einstein’s second sentence extracted from the same paper. Its significance appears to have gone undetected hitherto.
12. Do i-Meteons Carry Dark Energy?
Einstein considers a number (n) of points [Punkte] “(e.g. molecules)” he says, moving in a volume v0. Then he writes (our translation, our emphasis): “Apart from those, there may be in this space arbitrarily many other moving points of some kind or other [Punkteirgendwelcher]”, adding: “we do not make any assumptions about the laws according to which the points considered move in space, except that as far as their motion is concerned no part of space and no direction is preferred above others.”
Moving points of some kind or other… Our concept of i-meteons moving about randomly, i.e. with “no direction preferred above others” and without being subjected to the l = cd constraint, had not been invented then. And so, at least in this regard, we are moving in Einstein’s footsteps (or him in our footsteps, retrospectively). But what kind of energy do these meteons carry?
13. Where Is Dark Energy Hiding?
Dark energy… Right off the bat let us be extremely prudent―for a simple reason. In his Lectures on Physics the great Richard Feynman warned us candidly (our emphasis): “It is important to realize that in physics today we have no knowledge of what energy is [13] .”
We do not know with certainty what Dark energy is, but, as a result of the outstanding investigations Alexandria theoretician Mohamed S. El Naschie has carried out and published recently, its whereabouts in the universe may have been localized. According to M. S. El Naschie, writing in 2015 [14] (our emphasis), “ninety-six percent” of the energy present in the universe is concentrated “at the boundary of the universe”. The rest of the energy is “inside the universe and we call it ordinary energy”. Why “ordinary”? “Because we can measure it” while the dark energy part of the total energy, “being concentrated for all practical purposes at infinity”, cannot be measured directly”. If this be, how do we know that it is there? “We perceive its effects only as a negative pressure forcing the universe to accelerate its expansion” In brief (in other words) “dark energy and ordinary energy are basically one and the same thing, manifested however in different ways depending on scale and topology of spacetime”. And Mohamed S. El Naschie to conclude: “We could do a back of an envelope calculation to come to this momentous result.”
14. Thunder in Spacetime
If our analysis holds true, then dire consequences follow:
1) Einstein’s “energy quanta”―photons in modern terminology―are e-meteons which carry pulses of “ordinary” (electromagnetic) energy and travel at a prescribed speed, the same for all such meteons―the speed of light, c, as a consequence of the “order” constraint which affect them. This ascribes an entirely new physical significance to said speed.
2) Not so for i-meteons. Not compelled to maintain relations of “order” with each other as e-meteons do, they move about freely as Einstein seems to have anticipated when he invented them unknowingly (unwittingly) in 1905, stating: “There may be in this space arbitrarily many other moving points of some kind or other [Punkteirgendwelcher]”.
3) If e-points in motion transport “ordinary energy”, we are then led to believe (to assume) that i-points in motion transport “dark energy” (else there would be no notable difference between the two). In which case we are entitled to say:
4) The Phantom―Dark Energy―is here with us, occurring in the System of the World in the form of i-meteons travelling at speeds not related to the speed of light. It remains to discover why we have (apparently) failed to discover them (experimentally) so far.
5) But maybe we have found them―unknowingly. Indeed, what about these “virtual photons” and other “virtual particles” that physicists are so keen to speak of, saying that they are “off mass shell”, can progress “backwards in time”, do not “conserve energy” and can travel faster (or slower?) than light…
15. The Loch Ness Monster Is Back!
Einstein sought a relation between the Planck constant and the Boltzmann constant, ending up with a relation between time duration and the degree Kelvin of Absolute temperature. The “Planck time” is defined as the time a photon―a e-meteon in our (new) terminology―traveling at the speed of light takes to cover a distance equal to the “Planck length”. Many physicists take this seriously, saying that the Planck time represents the “quantum of time”, i.e. the smallest measurement of time that has any meaning, and that it is equal to 10−43 seconds. No smaller division of time has any meaning, they say.
Let us calculate to what Absolute temperature above the Absolute Zero the Planck time would correspond, using the Einstein constant formula.
Readily done. It corresponds to (1/4.866) × 10−45+11 K, i.e. about 2 × 10−33 K.
If an object were to reach the “Planck temperature” of 1.41 × 1032 K (TP), the radiation it would emit would have a wavelength equal to the Planck length, i.e. 1.616 × 10−26 nanometers, at which point quantum gravitational effects would become relevant. At temperatures greater than or equal to TP, current physical theory breaks down because “we lack a theory of quantum gravity”. We have a favorite saying in situations such as this: “I have seen worse―but not often”.
16. The Ides of March
The month of March seems to have played a special role, at least at times, in Albert Einstein’s life. He was born in March (1879). In March of 1901, he “defined” himself as a “mathematical physicist familiar with absolute measurements”. In March of 1905, he invented his constant β which, in effect, makes the “Planck constant” and the “Boltzmann constant” disappear from sight in Quantum Physics. We invite the attentive reader of the present note to investigate what becomes of Quantum Physics (QP) when this is done. Quite simply this: the shaky tower of the “Planck units” System collapses in a Big Bang, leaving QP in a shamble. To be replaced by what?
As William Shakespeare had his Hamlet wonder [15] :
To be, or not to be: that is the question: Whether tis nobler in the mind to suffer The slings and arrows of outrageous fortune, Or to take arms against a sea of troubles, And by opposing end them?
To us, preparing to conclude this note, the task ahead is clear; we must “take arms against the quantum sea of troubles” and reinvent QP―perhaps on the basis of the System of the World that we have imagined in the context of which two “active principles”, the noX and the Xon, continuously but discontinuously generate little bangs which set off flurries of quantum meteorites―of meteons―transporting (electromagnetic) energy pulses at speeds not necessarily equal to the “speed of light”.
Active Principles?
17. Reinvent Quantum Physics―Do We Dare?
17.1. Anticipating Meteons
Not trying to keep track of dates too precisely; let us briefly survey the past history of points in motion.
In 1784, Swiss physicist Georges-Louis Le Sage formulated a theory of gravitation grounded in the postulate of the existence of an aether made of “ultramondane particles” moving in space at the speed of light. This led English theologian Samuel Tolver Preston to express the idea in 1875 that aether is “rarefied mass” and mass “concentrated aether”, a view which received a profound echo in Cambridge with sir Joseph John Thomson and his Society for Psychical Research, and in France in the mind of College de France professor Paul Langevin, who held that matter is “liquefied aether”.
Going back in time further… According to Leibniz’s 1686 fundamental concept of an inherent vis motrix equal to mv2 for a body of mass m moving at the velocity v, Samuel Preston found, for v = c, an energy equal to mc2. This line of thought was revived in 1903 when, encouraged by his friend, the famed astronomer Giovanni Schiaparelli, Italian railroad engineer Olinto de Pretto published in Venice the extensive memoir that modern tenants of this line of thoughts regard as the first legitimate formulation (proof) of E = mc2.
And before all of them there was…
17.2. Newton, of Course
Wishing to be widely read and understood in 1687 by natural philosophers many (most) of whom lived on the continent, not in England, Isaac Newton wrote his Principia in Latin, the universal language then utilized by all scholars in civilized Europe. In the early years of the Eighteenth century he wrote his Opticks in English, language not commonly used then for the transmission of discoveries made in the field of Natural Philosophy (physics). This made it possible for him to formulate some of his alchemical inventions without fear of being severely ostracized by scholars, who surely would not take seriously a “treatise” written in English. In the Principia Newton would not have taken the risk of writing (in Latin) a sentence such as this, which figures in his Opticks in plain English: “The changing of Bodies into Light, and Light into Bodies, is very conformable to the Course of Nature, which seems delighted with Transmutations” [16] .
Delighted with Transmutations…
Not convinced? Then read what Newton wrote in his Query 31, which is just about the last text he ever published in his lifetime: “For we meet with very little Motion in the World, besides what is owing to these active Principles” (our emphasis). He explained:“If it were not for these Principles, the Bodies of the Earth, Planets, Comets, Sun, and all things in them, would grow cold and freeze, and become inactive Masses; and all Putrefaction, Generation, Vegetation and Life would cease, and the Planets and Comets would not remain in their Orbs” [17] .
Newton also recognized the high significance of Duality in the Universe: it is not by accident that we have two hands and two eyes…
Active Principles… Duality… In our endeavor we identified two “active principles”, the noX and the Xon (duality) and we assigned to them the task of transporting, while spinning, each a quantum (fixed amount) of action, a concept neither Newton nor Einstein “had” in their days―Einstein because his “quantas” do not carry a “unit” amount of action―in fact the very concept of dynamical action was foreign to him throughout his scientific career, he was strictly a believer in “energy” not a believer in “action”. Newton by contrast, if he did not refer to Actio by name, spoke openly of Activity and of Centers, which are “Mathematical points” he said― Punkte, ?, 点, Amaphuzu, точки, Puntos… And Leibniz invoked the conatus, which is an “indivisible minimum of motion”―in brief, a quantum.
As for Einstein…
18. At the Length Truth Will out
In his play The Merchant of Venice (1596), William Shakespeare has his character Lancelot say it in a wonderful way: “At the length truth will out” [18] ―In the end, truth will come out.
It is not by accident but by deliberate choice that Einstein, in writing his Heuristic paper, avoided systematically, from beginning to end, using the Planck constant, i.e. the “constant of nature” which constitutes, all and by itself, the very foundation of Quantum Physics. He replaced it in his paper systematically, from beginning to end, by his own constant β, which has the unexpected dimension of a unit of time per Kelvin degree of Absolute temperature.
Facts are facts, we may choose to ignore them, but they remain facts.
It is also a fact―and facts are facts―that Einstein was not the “first inventor” in modern times of the relation m = E/c2―or of E = mc2 if you prefer. Newton once remarked: “Second inventors have no right”. Einstein acknowledged this simple fact himself goodheartedly in a (short) paper that he published in Annalen der Physik in 1906 [19] , stating unambiguously: “... die einfachen formalen Betrachtungen, die zum Nachweis dieser Behaup- tung...―... the purely formal considerations that need to be performed to demonstrate this assertion [m = E/c2] have been developed for the main [our emphasis] in a work by...” and he spelled out explicitly the name of the min ing engineer genius mathematian who presented his demonstration of said assertion in the Festschrift which was published in Leiden on December 11th 1900, a document anyone can consult at his/her leisure ever since [2] . As to what happened later... That’s another story, as sir Rudyard Kipling would have said. What’s in a name anyway?
19. Epilogue
At a time when experimental physics and technology have reached heights undreamed of a century ago, Quantum Physics remains awkwardly contrived under a pile-up of obsolete or ill-defined concepts. Which enterprising young or not so young theoretician presently residing somewhere on one of the Five Continents after having read this note will become the new Einstein daring to undertake and carry out to fruition the perilous task consisting in taking these steps:
1) Discover and reveal to the World of physics the theoretical and the practical significances of the surprising equation
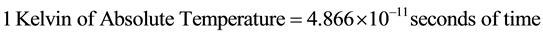
that Albert Einstein―the Albert Einstein of legend―implicitly proposed in his 1905 Heuristic paper. This equation constitutes the Great invention (reminder: discovery of a hidden treasury) that he made during his Annus mirabilis―(not reproducing an invention previously made by someone else before him) and which has remained unnoticed hitherto.
2) Reinstate the elementary quantum of action (h)―perhaps under a new name, such as the “elementary quantum of motion”―at the heart of a rejuvenated Quantum Physics.
3) Demonstrate once for all the detrimental inanity of the Planck universal system of units.
4) Incite physicists to stop referring to the illusory “Planck scale”―Planck length, Planck time…―in their calculations.
As for Dark energy…We found it in this note in the form of an ingredient―an attribute?―carried off in the System of the World by i-meteons―i-quantum meteorites―at speeds not related to the speed of light. To us thus, in this note, clearly the Phantom (Dark energy) is in the House (Figure 2). M. S. El Naschie sees it being concentrated “at the boundary of the universe” (our Heading 12), two projections which require to be reconciled. We note meanwhile, however, that were our analysis to prevail it would facilitate rather than impeach M. S. El Naschie’s proposal to construct a “nanoreactor” to tame the elusive Dark energy for humanity’s benefit [20] .
20. Conclusions
Incidentally, in the title of this note we used the qualiiier Intriguing. We chose this qualifier deliberately in view of its multiple linguistic and philosophical connotations interesting, fascinating, absorbing, exciting, engaging, gripping, stirring, stimulating, curious, compelling, amusing, diverting, provocative, beguiling, thought-pro- voking, titillating, engrossing, tantalizing… [21] .
As for Einstein…In his 1905 “Heuristic” paper, he attacked (surreptitiously) the Planck constant, i.e. the elementary quantum of action, which is at the heart of Quantum Physics―he made it disappear! But he did not attack (criticize) Planck himself directly, quite to the contrary―for a very good reason: his “correspondent” in Berlin―his accomplice, his mentor, his secret “protector” during his Annus mirabilis (and for many years thereafter) was (Figure 3)…
Max Planck.
Figure 2. Dark energy. Is the Phantom in the House? https://encrypted-tbn3.gstatic.com/images?q=tbn:ANd9GcTL3lANQoAoDdDjvf2hqKH7THbByfmP8UE9GKpileNeK_uggzpVL
Figure 3. Einstein (left) with Max Planck. https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcSOd0Fi9Mgr3stO4Q84WsnUXmBHD83hUkVoi6xaiyav9rCyxnl1
Acknowledgements
We are indebted to Dr M. S. El Naschie for calling our attention, as we undertook to write this note, to the problem of locating Dark energy in the universe, and to Ms. Clara Gao, to Ms. Kelly Sang and to Ms. Freya Zhang, JMP Editorial Board Assistants, for their valuable help and advice in properly formatting the manuscript for publication in this journal.
Cite this paper
Jean-PaulAuffray, (2015) On an Intriguing Invention Albert Einstein Made Which Has Gone Unnoticed Hitherto. Journal of Modern Physics,06,1478-1491. doi: 10.4236/jmp.2015.611152
References
- 1. Einstein, H. (1901) The Collected Papers of Albert Einstein, Vol. 1: The Early Years, 1879-1902. Princeton University Press, Princeton.
http://www.the-scientist.com/?articles.view/articleNo/8871/title/Albert-Einstein-Looks-for--a-Job/ - 2. (1900) Archives néerlandaises des sciences exactes et naturelles. Recueil de travaux offerts par les auteurs à H. A. Lorentz. Ser II, Nijhoff, The Hague, 252-278.
http://physicsinsights.org/poincare-1900.pdf - 3. Auffray, J.-P. (2015) Journal of Modern Physics, 6, 878-889.
http://dx.doi.org/10.4236/jmp.2015.67092 - 4. http://www.chemteam.info/Chem-History/Stoney-1894.html
- 5. Stoney, G.J. (1881) Philosophical Magazine, 5, 381-390.
http://dx.doi.org/10.1080/14786448108627031 - 6. Planck, M. (1899) Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin, 5, 440-480.
https://en.wikipedia.org/wiki/Planck_units - 7. http://www.eoht.info/page/Ostwald+happiness+formula
- 8. http://en.langenscheidt.com/german-english/allotria.4
- 9. http://bestfountainpenreview.com/waterman-pen/
- 10. Einstein, A. (1905) Annals of Physics, 17, 132.
http://www.esfm2005.ipn.mx/ESFM_Images/paper1.pdf - 11. https://claesjohnsonmathscience.wordpress.com/article/the-desperation-of-planck-yvfu3xg7d7wt-79/Collected
- 12. Collected Quotes from Albert Einstein.
http://rescomp.stanford.edu/~cheshire/EinsteinQuotes.html - 13. Feynman, R. (1964) The Feynman Lectures on Physics, Vol. 1, Chapter 4.
http://www.feynmanlectures.caltech.edu/ - 14. El Naschie, M.S. (2015) Advances in Pure Mathematics, 5, 560-570.
http://dx.doi.org/10.4236/apm.2015.59052 - 15. http://www.nosweatshakespeare.com/quotes/hamlet-to-be-or-not-to-be/
- 16. Newton, I. (1730) Opticks Query 30, 375.
http://www.gutenberg.org/files/33504/33504-h/33504-h.htm - 17. Newton, I. (1730) Opticks Query 31, 400.
http://www.gutenberg.org/files/33504/33504-h/33504-h.htm - 18. Shakespeare, W. (1596) The Merchant of Venice.
http://www.phrases.org.uk/meanings/390200.html - 19. Einstein, A. (1906) Annalen der Physik, 20, 627-633.
- 20. El Naschie, M.S. (2015) Journal of Modern Physics, 6, 1321-1333.
http://dx.doi.org/10.4236/jmp.2015.69137 - 21. http://www.thefreedictionary.com/intriguing




