Received 1 June 2015; accepted 1 August 2015; published 6 August 2015

ABSTRACT

Agreed with the Lorentz transformations, a multidimensional treatment of motion of elementary particles with the fundamental speed (upper limit of the speed of light) in six-dimensional Euclidean space in Compton neighborhood of observed three-dimensional space is given. Thereby it is supposed that the proper time of any elementary particle is proportional to the path traversed by it in the extra space. By the available experimental data [1] , these suppositions are allowed to find the photon proper energy, 1.44 × 10⁻⁵ eV. It is shown that the difference between the fundamental speed and speed of high-energy photons, in the projection on the three-dimensional space, is negligibly small.

Keywords:

Proper Photon Energy, Dispersion of Light in Vacuum

1. Introduction

In Ref. [1] an experiment is described in which, at the level of precision 3σ, a dependence of the speed of photons in the vacuum of their energy is obtained. It is shown that photons with energies 12.7 GeV are moving faster than the photons of the visible spectrum at 5.1 mm/s. This corresponds to an increase in the relative speed of the photons by the amount 1.69 × 10⁻¹¹. As possible reasons for this dispersion, in Ref. [1] the influence of gravitational fields and virtual photon decays into an electron-positron pairs are indicated. However, multi-dimen- sional interpretation of this dispersion is explained by the presence of proper photon mass (rest mass). The results of Ref. [1] give the possibility on the basis of multidimensional physics to explain the dispersion of light in vacuum by photon rest mass as well to calculate this mass.

Multidimensional treatment of physical phenomena [2] - [4] is based on the principle of simplicity [5] . It is important that there is no need to tie the theory to the pseudo-Euclidean space-time, as in Euclidean space with the number of spatial dimensions greater than three the Lorentz transformations are obtained elementarily under the above postulates [2] .

2. Motion of Elementary Particles in the Compton Neighborhood of Three-Dimensional Space

Following the principle of simplicity, we assume that all elementary particles, including photon move in the six-dimensional Euclidean space with fundamental velocity equal to the upper limit (c) of the speed of light at Compton distance 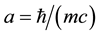from the observed three-dimensional space; here m is the proper particle mass (rest mass). It follows that the proper speed of elementary particles (at rest in X) in the extra space is the same fundamental value c, independent of the particle energy. We also believe that the proper time of an elementary particle is proportional to the length of the path traveled by it in the extra space [2] .

At the same time we allow a slow change of c with the expansion of the three-dimensional universe in the space of a higher number of dimensions. The universe has a finite size and very uniform in large cosmological scales. Therefore, it is a three-dimensional sphere. On small cosmological scales, the three-dimensional space of the universe can be considered locally Euclidean.

With this definition of proper time, the twin paradox is simply explained: the faster an object moves in three-dimensional subspace (X), the lower the speed of elementary particles in the complementary subspace, and hence slower flows its proper time.

We believe that in the complete space the formulas of Newtonian mechanics are applicable with a suitable choice of time specified below, and that the position of the particle is fixed by observer in three-dimensional Euclidean projection onto the subspace 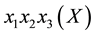tangent to the three-dimensional universe as a three-di- mensional sphere embedded in a complete space. The point of tangency occurs at the position of the observer in X.

From the existence of macroscopic objects in the three-dimensional universe, it follows that the elementary particles move in the extra space on finite paths in sufficient proximity to the three-dimensional universe to the observed interaction of elementary particles could occur. This means that in the extra space on every elementary particle acts a cosmological force perpendicular to the three-dimensional sphere. It keeps the particles at a short distance (a) from this sphere. Otherwise, the elementary particle is infinitely removed at the speed of light from our three-dimensional universe in a straight line in the complete space. Such forces (of type the Lorentz force in which the charge role plays the mass) are the reason for trajectories of elementary particles to be compacted in the extra-dimensional subspace withstanding to centripetal forces in it. This enables the formation of atoms, molecules and the macroscopic bodies.

We believe the distance of an elementary particle of the three-dimensional subspace is equal to Compton radius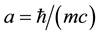, and the total space is the six-dimensional Euclidean one because the simple interpretation of spin and isotopic spin requires just such a value a and at least three additional spatial dimensions. In this case, at the absolute value the angular momentum in the complete space is equal to. This yields a simple interpretation of Heisenberg uncertainty relations, de Broglie waves, Klein-Gordon equation, the intrinsic magnetic moment of the electron, CPT-symmetry [2] . In the six-dimensional space the spin and isotopic spin are treated as projections of the total angular momentum to the subspace X and its complementary subspace Y, respectively, and the intrinsic magnetic moment―as a result of rotation of the charge with the fundamental speed (c) in Y along the orbit of the Compton radius.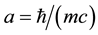

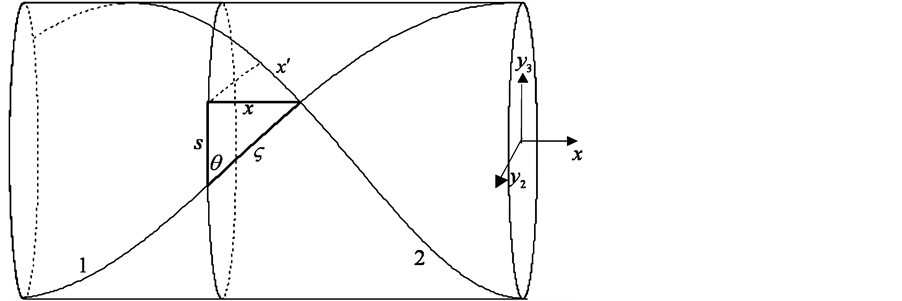
All directions in the subspace Y of considered Euclidean multidimensional space are perpendicular to any directions in three-dimensional subspace X. Therefore, the projections ds and dx of a displacement cdt of a particle moving with the fundamental speed c in complete space of any number of dimensions on Y and X, respectively, are connected by Pythagorean theorem: 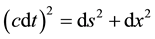where cdt is displacement of the particle in the complete space per time dt (see Figure 1). Hence we obtain the metric of relativity theory.

In the complete space free in X particle moves along the tube of Compton radius a (envelope of geodesics). The tube axis belongs to the three-dimensional subspace X, and the surface of the tube is spaced from the axis by the amount a in subspace Y. Interval ds is a displacement of a particle along a directrix of the tube, dx―along the tube axis.

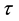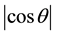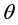Natural and consistent with Lorentz transformations measure of the proper time of a particle is its path length in the complementary subspace Y. Therefore, we assume the proper time of the particle is proportional to this path. It is also proportional to where is the inclination angle of helical line on the motion tube (Figure 2). Therefore, if a particle makes one revolution around the axis of the tube per the proper time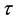, then on the clock of the stationary observer against which the particle moves along the tube at a rate 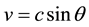it occurs per time.

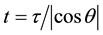Given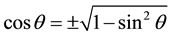, we find

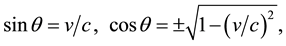(1)

where the upper sign before the square root refers to a particle rotating around the tube axis in the positive direction, the bottom―to its antiparticle, rotating in the opposite direction. This choice of the sign corresponds to the following relation between the intervals of proper time 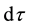of the particle (or antiparticle) and time of a stationary observer:

. (2)

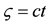
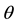
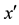
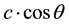
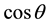
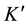
In the fixed frame of reference K a particle has a velocity component along the directrix equal to. The proper time of the particle in terms of a stationary observer, according to (2) is also proportional to, so that the particle in its proper reference frame moves with the speed c.

Note that in contrast to the theory of relativity, which for determining of the proper time is used the hypothetical massless non-dispersive photon, in a multidimensional interpretation of the quantities the real elementary particles with non-zero mass at rest are involved, while the proper time of the particle is proportional to the path traversed by it in the complementary subspace Y.

Momentum of a particle at rest in X is a vector directed along the tangent to the trajectory at the point at which the particle is located in X at present. It is equal in magnitude to mc, the product of the mass m of the particle and its velocity in Y. This value is equal to its proper momentum in relativistic mechanics.

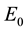
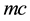
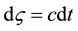
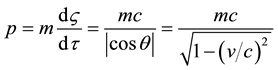
The particle proper energy, by definition, is equal to the product of the momentum at rest and the particle velocity along the trajectory, so. In general, the total momentum of a particle is a vector directed along the tangent to its helical path on the tube. Its magnitude p is equal to the product of the mass m of the particle and the path traversed by the particle in complete space per the proper time spent on this path:

(3)

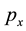
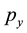
This is the relativistic formula for the total momentum of a particle. Projections and of the total momentum on the generatrix and directrix of a tube are equal to

(4)

respectively. This is the relativistic formula for the total momentum of a particle. In relativistic mechanics these projections are called the spatial and temporal components of the four-momentum of a particle, respectively. The total energy of a particle E is the product of the total momentum p and the speed of motion c along a helical line:

(5)

This value is the total relativistic energy of a particle. Note that the ratio of the total energy to the total momentum of the particle is the same as that for a photon. This is yet another common property of light and substance.

Formulas (4) and (5) for and E have the same form as in the standard relativistic mechanics [6] , but now c is a fundamental constant equal to the upper limit of the speed of light. The notion the total momentum of a particle, introduced by the formula (3), in the standard relativistic mechanics is absent at all.

From (4) and (5) we find and

, (6)

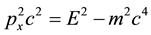
as in the standard relativistic mechanics, where (6) is used for the obtaining m.

Formulas (2)-(6) also hold for the curved axis of a motion tube because in any case all normal sections of such a tube are perpendicular to any directions in the subspace X to which belongs the axis of the tube.

It is impossible to trace the motion of particles in the additional space, or directly measure the length of the path traveled by it in this space. But to justify the theory it is possible to compare its results with the observations that here and in [2] -[4] [7] and done. In particular, the application of Fermat’s principle to the particle trajectory in the six-dimensional Euclidean space leads to Papapetrou metric [2] [8] , which coincides with Einstein metric in the post-Newtonian approximation. In Ref. [4] compared the results of the simplest interpretation of the expansion, in the six-dimensional space, of the Universe as a three-dimensional sphere, with the observational data [9] and the standard cosmology, depending on the cosmological redshift. With setting parameters of the theory [4] , the Hubble constant is H₀ = 60.4 km/s Mpc. The local value of Hubble constant that obtained from local Cepheids without using the Einstein equations is H₀ = 60.9 ± 1.3 km/s Mpc wile from global Cepheids it is H₀ = 62.3 ± 1.3 km/s Mpc. The determination of H₀ from the Sunyaev-Zeldovich effect gives H₀ = 60 ± 3 km/s Mpc [10] .

In standard theory the mass is an invariant defined by equation (6) which remains true also in the multidimensional theory. If we assume that a photon moves with velocity c only in our three-dimensional space, then according to (5) or (6), the energy e of the photon will be finite only when m = 0. If we consider that the motion of particles with velocity c occurs in the complete space, including the additional space as it is assumed here, the velocity v will less than the speed c. Then the photon energy remains finite and in the case non-zero.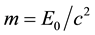

Lorentz transformations are the essence of the theory of relativity. Their interpretation is based on the properties of hypothetical massless photon moving in three-dimensional space in the reference frame of the observer at the speed of light and does not depend on the energy of the photon. However, the Lorentz transformations are valid as well in multidimensional Euclidean space, if all elementary particles have non-zero rest mass, moving in a complete space with the same fundamental speed equal to the upper limit of the speed of light, and the proper time of the particle is proportional to the length of the path traveled in the extra space.

Euclidean space contains only the spatial coordinates. To introduce the time coordinate there is not necessary because the proper time of the particle is a function of its displacement along the spatial coordinate axes of the extra space. Difficulties of the standard theory are caused by implicit assumption that the particles move in three-dimensional space, rather than in the complete space. The interpretation of the experimental results is also made in this assumption.

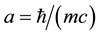
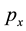
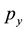
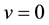
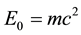
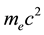
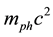
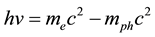
The formulas (3)-(5) are obtained in the assumption that the formulas of Newtonian mechanics are applicable to the particles moving with the fundamental speed c in the complete space at Compton distance from our three-dimensional space if the proper time of an elementary particle is proportional to the path traversed by it in the extra space. Formulas (4) and (5) for, and (6) for E have the same form as in the standard relativistic mechanics, but now c is a fundamental constant equal to the upper limit of the speed of light. For this reason, these values are numerically different, although very little from the corresponding values of the special relativity. It can be determined experimentally. For, the total energy E is reduced to the rest energy. This is seen on the example of the electron-positron annihilation. Here the rest energy of the electron (positron) minus the rest energy of a photon is transformed into the photon kinetic energy.

The main conclusion from this is the need for taking into account the motion of the particles in the additional space.

3. Speed Dispersion of Photons

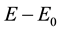
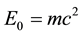
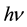
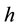
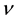
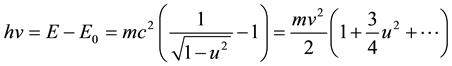
The kinetic energy of the elementary particle is, by definition, equal to the energy difference of the total energy e represented by the formula (5), and the rest energy. For a photon, it also is equal to, where is the Planck constant, is frequency of light, so that for the photon we have

,

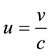
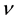
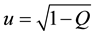
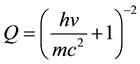
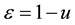
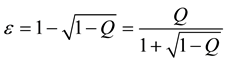
where, is the speed of a photon in the projection onto the subspace X. Hence, , where. In this case, the deviation of the relative velocity of a photon is equal to

.

To reconcile these formulas with the experimental data should be put mc² = 1.4415 × 10⁻⁵ eV. By this at the wavelength 5 × 10⁻⁵ cm we have: hv = 2.48 eV, Q = 3.379 × 10⁻¹¹, ε = 1.69 × 10⁻¹¹. At twice the wavelength hv = 1.24 eV, Q = 1.352 × 10⁻¹⁰, ε = 6.759 × 10⁻¹¹. At less than half the wavelength hv = 4.959 eV, Q = 8.448 × 10⁻¹², ε = 4.224 × 10⁻¹². At hv = 12.7 GeV, Q = 1.288 × 10⁻³⁰, ε = 6.442 × 10⁻³¹.

Compton photon radius 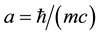is strikingly large in comparison with Compton radiuses of other elementary particles. It is a macroscopic quantity: a = 1.36 cm.

Figure 3 shows the function 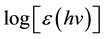depending on the photon energy. Figure 4 shows the same dependence, but for a rapidly changing part of the function.

4. Conclusions

Based on the multidimensional interpretation of motion of massive elementary particles in the complete space in the Compton neighborhood of the observed three-dimensional space X, it is shown that if the photons have the proper energy mc² = 1.44 × 10⁻⁵ eV, whence m = 2.57 × 10⁻⁴¹ kg, the dispersion of their speed in X is the same as in the experiment [1] .

The proper energy of photon, like of any other elementary particle at rest in the reference frame of observer, is the energy of motion in the extra space.

Fundamental velocity c is the velocity of the particle in the complete space.

The speed c negligibly little differs from speed of the high-energy photons in the projection on the three-di- mensional space.

The formula for the photon energy in the case electron-positron annihilation taking into account the motion of the particles in the additional space is obtained.

Cite this paper

I. A.Urusovskii, (2015) Multidimensional Treatment of the Observed Dependence of the Speed of Photon on Its Energy. Journal of Modern Physics,06,1220-1226. doi: 10.4236/jmp.2015.69126

References