Received 3 March 2015; accepted 17 March 2015; published 19 March 2015

ABSTRACT

We compute the dark energy and ordinary energy density of the cosmos as a double Eigenvalue problem. In addition, we validate the result using two different theories. The first theory is based on Witten’s 11 dimensional spacetime and the second is based on ‘tHooft’s fractal renormalization spacetime. In all cases, the robust result is E(O) = mc²/22 for ordinary energy and E(D) = mc²(21/22) for dark energy. Adding E(O) to E(D) we obtain Einstein’s famous equation which confirms special relativity, although it adds a quantum twist to its interpretation. This new interpretation is vital because it brings relativity theory in line with modern cosmological measurements and observations. In particular, we replace calculus by Weyl scaling in all computation which is essentially transfinite discrete.

Keywords:

Double Eigenvalues, Weyl Scaling, Magueijo-Smolin Energy Formula, Dark Energy, Einstein’s Relativity, E-Infinity Theory

1. Introduction

The present work looks at the major cosmological problems associated with the energy density measurement of the entire universe [1] -[11] . We tackle the problem once again from a novel angle, namely the double Eigenvalue problem computation [12] -[19] . Subsequently, we validate our results using Witten’s M-theory [5] [6] and ‘tHooft’s fractal renormalization spacetime [3] . It is important to understand from the outset that our main computational tool is to convert calculs to Weyl scaling to deal with the discrete character of quantum high energy physics [8] .

2. Background Information

2.1. The SU(2) and E8 Lie Symmetry Groups through the Transfinite Looking Glass

In what follows and for later use, we will put SU(2) and E8 Lie symmetry groups as well as two and three Stein spaces under a transfinite microscope to reveal their inner fine structure as E-infinity Cantorian fractal form [20] - [24] . There are 3 generators in SU(2) given by [21] [24]

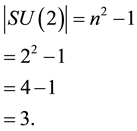(1)

For E8 on the other hand we have 248 generators, which means 496 generators for E8E8. Both groups have extremely important applications outside of pure mathematics, in particular SU(2) is a subgroup of the standard model of high energy quantum particles dealing with the weak force while E8 underpins the prominent theory of superstrings [22] - [24] . The point is that the fundamentals of high energy physics require that we must include 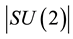on the right side to balance the E-infinity conservation of symmetries equation [5] [6]

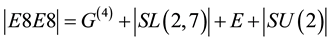(2)

where E is the degrees of freedom of the electromagnetic field as represented by the integer value of the inverse fine structure constant, 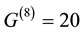are the degrees of freedom of pure gravity in super space of (D = 8) compatible with the rank of E8 and is equal to 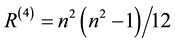for n = 4 of Riemannian tensor of Einstein gravity (n = 4) while SL(2,7) is the symmetry group of Klein’s modular space for which |SL(2,7)| = 336. Consequently we have [6]

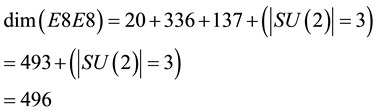(3)

exactly as should be. However we know that the different quantities of the right hand side could not be Weyl scaled, i.e. “differentiated” or “integrated” by being converted into each other unless they are all the same quantities but “measured” at different energies which means at different scales. It was the systematic application of E-infinity theory and its golden mean counting number system which revealed that adding or subtracting the exact transfinite values arsing from the various quantum entanglement probabilities such as that of Hardy, Immirizi, Unruh 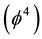and El Naschie 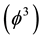which ensures symplecticity and thus the applicability of Weyl scaling calculus. In particular the ‘tHooft k [3] given by as well as

form the transfinite tale of are indispensible for showing that the following transfinite or entanglement correction leads to the following E-infinity exact expression [5] [6] [8] [24] - [3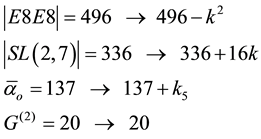4]

(4)

That way however we see that 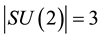is already indirectly taken care of by the effects of entanglement correction. Therefore one could take the view that is not needed at all. Alternatively a transfinite form of SU(2) could be seen under a transfinite microscope to be formed by the following three components [34]

(5)

The first number on the right hand side is what gave |SL(2,7)| its fine structure adjustment, the second number is the |E8E8| transfinite correction while the third number is what gives its scaling “non-violation” with respect to |E8E8|, namely [34]

(6)

where as is easily verified [30] [34] . Another, and maybe more fundamental interpretation, is to take the view that k² and k_o are probably entitled to be called quasi particle as = 0.1803393 has been considered to be a ‘tHooft renormalon [3] . In fact counting particles reveals the quasi-particle nature of k, k₅ = k_o and k² provided we count in the fractal-fuzzy or transfinite logical way [34] . Proceeding in this way we realize that the 12 gauge bosons of the standard model, namely |SU(3)| + |SU(2)| + |U(1)| = 8 + 3 + 1 = are not 12 but really 14 quasi particles with a counting fractal weight equivalent to particle [30] [34] . More explicitly these are one photon counting as, 3 electroweak photons counting as 16k and 8 gluons of thestrong force counting as. To these elementary particles we have one Higgs count- ing as k₅ = k_o = and one graviton counting ask² [3] [34] . The final fractal sum or total topological mass, i.e. asymptotic length of a corresponding field generalizing the Higgs field is neither 12 nor 14 but where is self entanglement of a single quantum particle equivalent to Unruh’s thermal bath or dimensionless temperature as observed in the Rindler wedge [7] . We note that is equal to

[30] [34] .

Next we would like to reason why 16k could also be interpreted as the additional fine structure of SL(2,7). This comes from the fact that |SL(2,7)| = 336 is actually eight copies of the Klein orbit 42 so that 336 = (8)(42). On the other hand 42 is really the truncation of ten copies of the Hausdorff dimension = 4.23606799 so that ten copies of gives 42 [30] [31] [33] . Consequently the exact transfinite result should be 42.3606799 times 8 which gives the transfinite continuation of |SL(2,7)| to [34]

(7)

exactly as anticipated. In fact we could count the 8 copies also using the fractal fuzzy logical way as

where is Hardy’s entanglement [5] [6] and find the dimension of an M-mani- fold related to the sum of all the 17-fractal two and three Stein spaces where the classical Einstein space is a one-Stein space [33] . To show that it is exceedingly illuminating to note that the sum of all the dimensions 17 two and three Stein spaces is exactly 686. When transfinitely corrected, the sum turns out to be exactly equal (5) where. That means [30] [33]

(8)

Now for 8 + one finds on the other hand

(9)

Clearly two copies of dim M gives us the sum of the dimensions of the 17 Stein spaces

(10)

in complete agreement with what we said earlier on [5] [6] [33] .

2.2. E-Infinity Arithmetic and Weyl Scaling as a Discrete High Energy Quantum Calculus

Now is the time for us to look in some detail at the Weyl scaling calculus form of E-infinity [8] . It is a well known fact that the ratio of two successive numbers of the Fibonacci growth law converges towards the golden mean. From this many other results follow and we could thereafter formulate two well known fundamental theorems:

Theorem 1: Any positive integer can be written uniquely as the sum of nonconservative Fibonacci numbers of the “F” series (i.e. the Fibonacci series).

Theorem 2: Any positive real number can be represented uniquely as a sum of nonconservative numbers from the infinite series between and, i.e. the series

From the above and particularly theorem No. 2 we see that the series is like a number system to the base of 2. Furthermore the F and series can easily be used to show that can be written as the sum of and where a and. That means

(11)

Therefore we can write

(12)

In fact something similar to the above recursive formula turned out to be an excellent example of noncommutative space dimensional function [30] [32] which is nothing more or less than Penrose compactified hyperbolic fractal tiling [5] [6] . This dimensional function we give here, not for the sake of completeness but because it represents the dimensional function of E-infinity theory in the K-theoretical form, namely [30] [32]

and. (13)

The exact E-infinity formula corresponding to the above has been used extensively because it is a more compact and superior notation, termed the bijection formula

(14)

Applying to the quantum particle, i.e. the zero set and the quantum wave cobordism, i.e. the

empty set one immediately finds that

(15)

and

(16)

so that we may write

(17)

while

(18)

where D_MU is the Menger Urysohn topological dimension and D_H is the Hausdorff dimension [30] - [33] .

The next most important tool in our mathematical tool kit is Weyl scaling [5] [6] [30] [31] . This is in reality a substitution for calculus and scaling up corresponds to integration while scaling down corresponds to differentiation. Nothing could be simpler than our main scaling sequences as an example to explain what we mean. This we do next.

Let us start by scaling the inverse fine structure constant for a Cooper pair which means fermionic electron forming one boson, i.e.. We will scale it first down (differentiation) and then up (integration) using the golden mean exponents and. That way one finds

" " n = 2 26 + k Super symmetric quantum gravity coupling or the 26 bosonic string dimensions

" " 3 16 + k The extra 16 boson dimensions of Heterotic strings [30]

" " 4 10 The dimensions of super string spacetime [21]

" " 5 6 + k Compactified dimensions of super strings.

" " 6 4 ? k ‘tHooft dimensional regularization fractal spacetime [3]

" " 7 2 + 2k Fractal string world sheet

" " 8 2 ? 3k Complement of the string workd sheet [21] (19)

Note that 26 + k, 16 + k, 10, 6 + k and gives the Heterotic superstrings hierarchy when of ‘tHooft fractal renormalization spacetime [3] is set equal zero. An even more fundamental quantity is the first massless gauge boson of Heterotic superstrings, namely the well known No = 8064 reported for instance by Green in a classical popular reference in Scientific American entitled Super Strings, published September 1986 [35] . The corresponding transfinite exact value is given by ten copies of the intersection of the moduli space M(80) with the dimensionality of the fractal M-theory 11 +. Consequently we have

(20)

To see that this is the correct value we demonstrate first that

(21)

However the exact transfinite instanton density is 26 + k rather than 24 and the 336 is really 336 + 16k as explained earlier on. Consequently

(22)

exactly as anticipated [31] [34] . Now we examine the down scaling spectrum of N_o.

We will give here only the most important results, namely for n = 1, 2, 3, 4, 5 and 6 as well as the remarkable result for n = 16. Thus we have [5] [6] [33]

(23)

(i.e. R. Loll et al spectral dimension). Now the first five results when divided by superstrings dimensionality D = 10 give us the sum of all the E-line 8 exceptional groups, namely (4) = 548.328. The second gives us the compactified Klein modular space which is E-infinity holographic boundary 338.8854382. For n = 4 divided by 10 we fund the compactified electroweak unification value of, namely

. For n = 6 divided by 10 we find the well known modular lattice of Narian D = 80 [21] . Finally for 16 times Weyl differentiation one finds the fermions spectral dimension of R. Loll et al, namely D = 4.02 which measures the fractal spreading out of spacetime-like cosmic growth. It is not the El Naschie E-infinity spacetime Hausdorff dimension 4 + nor the ‘tHooft-El Naschie [3] but is something fundamentally related [5] [6] [30] [33] .

3. A Nonconstructive Derivation of an Extended Einstein Formula for Ordinary Energy and Dark Energy

We start with an epistemological reappraisal of Einstein’s formula from a Lagrangian approach viewpoint which incidentally Einstein never attempted. This Lagrangian is clearly dependant on a single generalized coordinate, namely the ordinary photon. Consequently the equation of motion could in principle be generated from a corresponding Lagrangian L() via the calculus of variation, i.e.

(24)

That way one finds the Eigenvalue to be the famous equation

(25)

However we know in the meantime extremely well that nature harbours far more than our classical photon and is really functioning based on 12 rather than a single messenger particle. In other words our submitted Einstein Lagrangian is missing eleven more generalized coordinates

To be precise the supposed Einstein Langrangian should have included 3 more SU(2) particles of the electroweak, i.e. the experimentally verified, , neutral current Z_o as well as the equally experimentally confirmed 8 gluons of SU(3) which together with the U(1) conventional photon form the basis of our current SU(3) SU(2) U(1) standard model of high energy physics. Not only that but from the physical theory of E-in- finity which is based on the mathematical theory of the highly structured E-infinity golden mean rings we know that the exact fractal number weight of the 12 bosons of the standard model is exactly which is the square root of and more over correspond to 14 rather than 12 particles [34] . From this mathematically firm results we can relax our approach momentarily and make an educated guess based on gauge theory, fractal self similarity and Weyl-Nottale scaling namely that an adequate correction of Einstein’s E = mc² could be obtained by scaling down the eigenvalue using the number of the missing generalized coordinates, i.e. messenger particles of the standard model [5] [6]

(26)

This must be taken in conjunction with either super symmetry or simply Newton’s kinetic energy so that we find at the end that

(27)

That means the ordinary energy-mass relationship should be [3] - [7]

E(O) = mc²/22, (28)

rather than simply E = mc² found for a single photon by Einstein. Now we ask ourselves where is the rest of the energy, namely mc²(21/22)? We could speculate scientifically that there is no rest of energy and that is all what we have. However we could let ourselves be guided by cosmological measurements and observations that the rest is the mysterious dark energy which is suspected to be behind the accelerated rather than decelerated expansion of the cosmos. That could indeed be the case for two reasons. First, it is because 21/22 mc² is indeed the indirectly measured missing dark energy. Second, and that is even more general, we know that the particle-wave duality is a fundamental real aspect of quantum physics and that the wave, although devoid of anything we could call ordinary matter, momentum or energy, has a real physical effect which goes as far as telling the particle where to go. Thus we could make a second educated guess and wonder if we are facing what in mathematics is called a double Eigenvalue problem rather than a single Eigenvalue problem. That would mean that our nonconstructively found 12 equilibrium equations defined via a 12 by 12 solvability determinant

(29)

possesses two Eigenvalues and not merely one Eigenvalue. The first Eigenvalue is that found earlier on E(O) = mc²/22 while the second is inferred from the physical-mathematical scenario to be

. The above problem could be solved easily via comparison theorems for combined Eigenvalue problems due to Southwell and Dunkerly [13] [36] . The corresponding formulas were widely used in the literature on vibration and buckling Eigen frequencies and critical loads. In E-infinity of high energy physics these comparison theorems were used as nested oscillators by Marek-Crnjac [36] . Since mass in quantum mechanics is basically frequency and consequently by Einstein’s equivalence frequency is also energy, we can combine the ordinary energy and the dark energy Eigenvalues as we do for buckling loads or frequency of oscillation. In other words we can write

(30)

Rearranging one finds

(31)

That means

(32)

Assuming that c in a fractal spacetime must be itself an expectation fractal value of a speed that varies between zero and infinity, we see that we can make the following identification ‘transformation’, namely [25]

(33)

or the dual core correspondence

(34)

It is an elementary task to insert these values in the double Eigenvalue formula and find that the result agrees completely with what we obtain from the corresponding Magueijo-Smolin famous extension of Einstein’s E = mc² [25] . Never the less what we did needs a little more elaboration. First in E-infinity theory the topological speed of light is given by an expectation constant transfinite value equal to the golden mean. Second, splitting spacetime into counter factual parts given by the Hausdorff expectation dimension and local part given by the pure entanglement of two Cantorian-fractal points thought outside spacetime, i.e. ten we see that corresponds to c² and corresponds to the intrinsic probability of Cantorian spacetime or its frequency, that is to say its intrinsic topological mass. Seen that way mc² of the Cantorian point in spacetime is which happens to be Hardy’s probability for quantum entanglement of two quantum particles and therefore gives per particle a dimensionless topological energy density equal. Moving now to the fat fractal voids between the zero set particle points of space, i.e. the empty set space we have a five dimensional Kaluza-Klein spacetime with a Kaluza-Klein topological mass equal to 5. That means E = mc² becomes now. The average energy is obviously the average of both energies. The first is the energy density of the quantum particle zero set and the second is clearly the energy density of the quantum wave empty set. The sum is

(35)

Consequently the average is

(36)

which leads to Einstein’s original equation

E = mc². (37)

The two other equations are consequently

(38)

for ordinary energy and

(39)

for dark energy. The sum of both energies gives Einstein’s equation

(40)

We stress again that E(O) and E(D) can be considered experimentally confirmed with high accuracy because they totally agree with the cosmological measurements of COBE, WMAP and Planck as well as the supernova observations [1] -[7] . In conclusion we may add that there is a very simple method to confirm the result of ordinary energy, i.e. 1/22 via the vacuum state of pure gravity applied to Einstein’s 4D space and Witten’s 11D space. The degree of freedom of pure gravity is given as is well known by

(41)

Noting that Einstein’s equation lives in d = 4 and Witten’s equation in d = 11 one finds the following ratio for the Lorentzian factor of E = mc², namely

(42)

and

(43)

4. Deriving the Lorentzian Factors of Dark Energy

Let us first recall the relation between Einstein spacetime and that of ‘tHooft fractal renormalization spacetime. The ratio of the respective dimensionality, i.e. D(‘tHooft) to D(Einstein) defines the dark energy coupling. Thus from [3] [26]

(44)

where, and D(Einstein) which is of course equal four, one finds that

(45)

where is Hardy’s probability of quantum entanglement. Regarding the nice properties of the golden mean arithmetic, one easily finds that

(46)

and therefore our coupling between the two spaces is given by

(47)

To show that the preceding in the meantime well known result for the dark energy density of the cosmos is far from being an ad hoc one, we show in what follows how it can be logically deduced from the general framework of superstrings and Witten’s fractal M-theory.

We recall that |E8| = Dim E8 = 248 and that the transfinitely corrected version is given by

. Now we have to take out of the massless gauge bosons the 11 + dimensions of the fractal version of Witten’s D = 11 M-theory. Since we are using two E8 exceptional Lie symmetry groups we have to then subtract which should not be confused with compactified bosonic dimensions even though they are numerically equal. Second we have to subtract the ‘tHooft coupling order parameter k. That way we have taken out all that is responsible for producing ordinary energy density. The ratio to the total of is consequently the dark energy density in the uni- verse. This conclusion is easily verified by a trivial computation and one finds

(48)

Some readers may still feel awkward about why we had to account for the k coupling in this way. To alleviate any doubt let us compute in a different way without super symmetry. This way we have only D = 4 and we know that the inverse non-super symmetric quantum gravity coupling is. The new point of view starts again with the following self explanatory ratio

(49)

Now that we did not take any super symmetric intersection, we must take the square root because the above expression represents squared. That means

(50)

Consequently

(51)

That way ‘tHooft k is not needed and the same result is of course found, namely that

(52)

exactly as before.

5. Conclusions

Einstein’s equation E = mc², without Einstein or in fact anyone else realizing until recently, consists of two quantum components. The first is the energy of the quantum particle E(O) = mc²/22, which can be readily measured. The second is the energy of what is actually energyless quantum waves E(D) = mc²(21/22). Obviously we say energyless because this is not ordinary energy and it is not a coincidence that it agrees exactly with the energy density of the presumed dark energy of the cosmos. Adding both energies together we are back to the classical relativistic equation of Einstein. These fundamental results were obtained in the last three years or so using various methods.

In the present paper the problem was also nonconstructively solved as a double Eigenvalue problem using the comparison theorems of Southwell and Dunkerley. In addition, we validated the results via Witten’s eleven dimensional theory as well as ‘tHooft’s fractal renormalization spacetime theory. The main computational tool introduced here was the golden mean Weyl scaling which could be viewed as a substitute for calculus [8] .

Cite this paper

Mohamed S. ElNaschie， (2015) Computing Dark Energy and Ordinary Energy of the Cosmos as a Double Eigenvalue Problem。 Journal of Modern Physics，06，384-395. doi: 10.4236/jmp.2015.64042

References