Journal of Modern Physics
Vol.06 No.05(2015), Article ID:55474,12 pages
10.4236/jmp.2015.65060
Influence of Silver Vapours on the Transport of Nitrogen Plasma Properties
Ahmed M. A. Amry1,2*, Mostafa M. Abd El-Raheem1,3, Gamal A. Yahya1,4
1Physics Department, Faculty of Science, Taif University, Taif, KSA
2Physics Department, Faculty of Science, Assiut University, Assiut, Egypt
3Physics Department, Faculty of Science, Sohag University, Sohag, Egypt
4Physics Department, Faculty of Science, Aswan University, Aswan, Egypt
Email: *a.amry25jan@hotmail.co.uk
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 October 2014; accepted 7 April 2015; published 9 April 2015
ABSTRACT
Theoretical investigation of nitrogen-silver arc transport properties and an arc plasma model in stationary state have studied at low temperature i.e. between 3500 K and 13,000 K at atmospheric pressure. Results showed that the presence of small amounts of metal vapours, which have low ionization potential such as silver, modify the plasma characteristics. The solution of Elenbaas-Hel- ler gives us some information about the effect of metal vapours emitted from electrode on the characteristics of the arc column. We concluded that a small fraction of metal vapours in the arc column modify the electric field, current and the axial temperature.
Keywords:
Arc Plasma, Transport Properties, Metal Vapours

1. Introduction
Metallic vapour emitted from electrode is a very important phenomenon affecting most interrupting electric devices. The injections of metal vapours, into the plasma, contaminate the plasma region. Despite the amounts of these “contaminants” may be small, the relatively low ionization potential of such additive may have a strong effect on thermodynamic, transport properties of the plasma and affects the decay of wall stabilized arcs. Most of the available information on it has been generated by theoretical calculation of Shayler, and Fang [1] , Abdelhakim et al. [2] , Ouajji et al. [3] . Some experiments have been designed to measure it by many workers Jaya Ram [4] , Airey et al. [5] , Devoto [6] , Andanson and Cheminat [7] .
2. Theory
The present investigation is concerned with a theoretical calculation of the electrical and thermal conductivity, for an arc plasma at atmospheric pressure contaminated with silver vapours.
These computations need complete knowledge of plasma composition. The method applied for the calculation is based on the following assumptions:
1) The plasma is in Local Thermodynamic Equilibrium (LTE).
2) The density of doubly ionized atoms, for T ≤ 14000 K can be neglected. The arc column considered in this calculations consists of the following species:
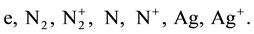
To determine the densities of the above mentioned species, a system of non-linear equations must be solved. The equations describing the densities are:
2.1. Saha-Eggerrt Equation
This equation relates the concentrations of the same type but with different ionization charge and can be written in the form:
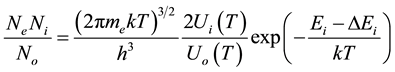 (1)
(1)
where  are the densities of the fundamental and ith state of the ion species A respectively;
are the densities of the fundamental and ith state of the ion species A respectively; 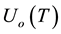 and
and 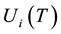 are there corresponding partition function,
are there corresponding partition function, 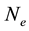 is the electron density,
is the electron density, 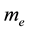 is the electron rest mass,
is the electron rest mass, 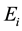 is the ionization potential of species A and
is the ionization potential of species A and 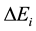 reduction in the ionization potential due to electric microfields in the plasma. The other symbols have their usual meaning.
reduction in the ionization potential due to electric microfields in the plasma. The other symbols have their usual meaning.
2.2. Lowering of the Ionization Potential
For a plasma with only singly ionized particles the following equation is used:
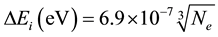 (2)
(2)
where 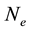 is in cm−3.
is in cm−3.
2.3. The Law of Mass Action for Nitrogen Dissociation
The ratio of neutral atomic nitrogen to molecular nitrogen is described by the law of mass action:
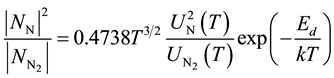 (3)
(3)
where 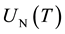 and
and  are the partition functions of N and N2 respectively and Ed is the dissociation potential of N2(= 9.76 eV).
are the partition functions of N and N2 respectively and Ed is the dissociation potential of N2(= 9.76 eV).
In this work, the tabulated values of the partitions by Drellishak et al. [8] have been used and that for Ag, are calculated according to the equation proposed by Lochte-Hojtgreven and Richter [9] .
2.4. Charge Equilibrium in LTE Conditions
The free electron density is related to the concentration of ions by the electric neutrality equation:
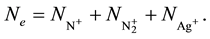 (4)
(4)
2.5. Dalton’s Law
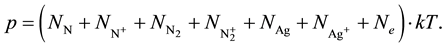 (5)
(5)
2.6. Percentage of Metal Vapour in a Gas
The fraction of silver X present in the arc column is specified by the equation:

Equations (1)-(6) are a closed non-linear system from which the electron density Ne can be deduced. This equation is solved using Newton-Raphson iterative method after this the densities of the other species are then easily calculate. Once the composition of the plasma is known, the computation of heat, mass, and momentum fluxes requires the knowledge of transport properties can be obtained.
3. Collisions Integrals
Accurate calculations of the electrical conductivity can be obtained by knowing the collision integrals (collisions cross-section) of the different interactions. These quantities are defined as:

where E is the relative energy, µ is the reduced mass of colliding particles:

and l, s are the two parameters that define the order of the collision integrals. Thus, the value of the above quantities can be calculated by performing the following integrals:
3.1. The Relevant Cross-Section Q(l)E
where b is the impact parameter.
3.2. The Classical Deflection Angle ϑ(b, E)
where rm is the distance of the closest approach of the two particles in the potential field V(r).
From the above expressions we can say that the problem of calculating Ω(l,s) reduces the knowledge of V(r). The binary collision can be classified into four categories in the thermal plasma.
3.3. Binary Collision
3.3.1. Charged-Charged Collisions
For calculating the collision integrals of charge-charge interaction, Liboff’s method [10] is used as described in Preuss [11] .
3.3.2. Electron-Neutral Collisions
1) Electron-Silver: The momentum transfer cross-section 
Then, we used the value of 

2) Electron-nitrogen: in this case the values given by Capitlli and Devoto [14] , for e-N and e-N2 are used in our program.
3.3.3. Neutral-Neutral Collisions
These collisions are N-N, N-N2, N-Ag, N2-N2 and Ag-Ag. We classified these interactions as follows:
1) Silver-silver and silver-nitrogen: For these interaction, we used Lenard-Jonse potential. The collision integrals calculated with potential are tabulated as a function of reduced temperature T* which is given by:
where ε is the maximum energy of attraction.
2) Nitrogen-nitrogen collisions: For these type of collisions the results of Capitlli and Devoto [14] of collision integrals are used.
3.3.4. Ion-Neutral Collisios
For N+-N collision, the results of collision integrals given by Capitelli et al [15] are used. The collision integrals for the other interactions are calculated.
4. Electrical Conductivity
The electrical conductivity σ is simply defined by the equation:
where J is the charge flux density and E is the electric field.
Because of their relatively high inertia the ions remain at rest, only the electrons moving. The electrical conductivity is mostly due to the electrons so that the Chapman-Enskog method poorly converges for σ. Thus the third approximation must be used to calculate the electrical conductivity. In this interpretation we used the following relation, descriped by Devoto [16] , to calculate σ to a third approximation:
where the coefficients qmp are functions of the collision integrals, temperature and density of the particles.
5. Thermal Conductivity
This physical quantity can be calculated using the following equation. proposed by Spitzer and Harm (Mitchner and Kruger [17] ):
where 


6. Stationary State
The equation of conservation of energy is used successfully to describe the arc plasma in stationary state and to calculate plasma parameters (temperature, electrical and thermal conductivity) of the cylindrical arcs. This equation relates the input electrical energy JE, due to the electric field E, to the losses in energy due to thermal conduction and radiation. Considering an optically thin wall stabilized arc at atmospheric pressure and neglecting the radial convection this equation can be written in the form:

where 

where λ is the thermal conductivity. Considering that the positive column cylindrical in shape, Equation (8) can be written the form:

This equation is a second order differential equation, which has single solution at r = 0 or

We can neglect the radiation in the case low temperature gas heating i.e. when the gas temperature in the arc is less than 12,000 K. Thus the radiation is not present in the balance. It is usually observed experimentally in the case of air heating at approximately atmospheric pressure and at not too high density of arc current. So, the main losses are determined by heat conductivity and the balance of energy of a plasma column looks like:

To solve this equation we used the assumptions used in the reference [18] .
7. Results
The computation of the electrical and thermal conductivities of nitrogen contaminated with electrode metal vapours from silver electrode necessitates complete knowledge of plasma composition. This composition was computed using the method mention above. The curves of Figure 1 represent the electron densities of nitrogen population, at different concentration of silver vapours, as a function of temperature. At low temperature (T < 8000 K) the electron density is due to the ionization of silver atoms while at high temperature (T > 10000 K) it comes from the ionization of nitrogen atoms. This is because of the ionization potential of nitrogen (EN ≈ 14.53 eV) is higher than that of silver (EAg ≈ 7.57 eV). The plasma composition for nitrogen-0.1% silver mixture as a function of plasma temperature at atmospheric pressure is shown in Figure 2.
Figure 3 shows the variation of the electrical conductivity as a function of temperature and concentration of silver vapour. At low temperature i.e., (T < 8000 K) the electrical conductivity is significantly enhanced by the presence of silver vapour. This is clearly due to the lower of ionization potential of silver in comparison with
Figure 1. Electron densities of nitrogen at different concentration of silver plasma at atmospheric pressure.
Figure 2. Plasma composition as a function of temperature for (N2-Ag) and X = 1% Ag at atmospheric pressure.
Figure 3. The electrical conductivity as a function of arc temperature at different concentration of silver vapours.
that of N2 molecule 
The thermal conductivity as a function of arc temperature at different concentration of silver vapour is shown in Figure 4. We remark that, the presence of silver vapour (about 0.1%) modify the thermal conductivity of the arc column. This can be interpreted as that an increasing in the electron density 
Figure 4. The thermal conductivity as a function of arc temperature at different concentration of silver vapours.
Figure 5. Radial temperature distribution for an arc of 0.25 cm arc radius at different concentration of silver vapours.
Figure 6. Radial distribution of the electrical conductivity for a 20 A arc at different concentration of silver vapours.
The variation of the axial temperature as a function of arc current for different concentration of silver vapour is plotted in Figure 7. We remark that at low current (~25 A), the axial temperature due to the presence of silver vapours, is maximum. By increasing the current, the silver arc electrode reaches melting temperature and the arc core strongly contaminated with silver vapour which decrease the axial temperature.
The arc characteristic, i.e. the relation between the electric field strength as a function of arc current is shown in Figure 8 at different concentration of silver vapours. We remark that the presence of metal vapour in the arc
Figure 7. Calculated evolution of axial temperature versus arc current intensity in N2-Ag mixture and pure N2.
Figure 8. The variation of the electric field with current for different concentration of silver vapours.
Figure 9. Evolution of axial temperature with the variation of arc current for different authors.
column modify the arc characteristic for a current of about 25 A. This result approaches the concept of the effect of increasing the electrical conductivity at low temperature region of the plasma.
The variant of axial temperature as a function of arc current for different workers is plotted in Figure 9. It can be seen that our calculations agree closely with those of Ouajji et al. [3] and Hermann et al. [19] until 50 A arc current and significantly lower with that of Sakuta et al. [20] .
8. Conclusions
We predict transport properties of silver-nitrogen gas mixtures in a temperature range from 3000 K to 15,000 K, which are important for an electric arc circuit breakers. When the metal vapours are mixed in with a gas of weak ionization potential; their influence is less clear than in a gas with a high ionization potential.
The presences of silver vapours in the arc column at atmosphere pressure have a significant effect on the temperature distribution, and voltage requirements [21] . This effect is, nevertheless, heavily dependent on the nature of the components of the mixture. When the metal vapours, ejected from electrode, are mixed in with a gas of low ionisation potential; their influence is less obvious than that in a gas with a high ionization potential. This can be observed, if the comparison between the axial arc temperature of an Ar-Ag [22] and N2-Ag mixtures is more strongly influenced by the presence of the silver than it is in a SF6-Ag mixture where the sulphur has a higher ionization potential than that is of copper [23] . The metal vapours have an appreciable influence on the electrical conductivity and on the radiation. The results show that the effect on electrical conductivity is preponderant in low-current arcs whereas that on radiation outweighs it at high currents.
Acknowledgements
The authors acknowledge financial support from Taif University for the project No. 2620-434-1.
References
- Shayler, P.J. and Fang, M.T.C. (1977) Journal of Physics D: Applied Physics, 10, 1659.
- Abdelhakim, H., Dinguirard, J.P. and Vacquie’, S. (1980) Journal of Physics D: Applied Physics, 13, 1427. http://dx.doi.org/10.1088/0022-3727/13/8/012
- Ouajji, H., Cheminat, B. and Andanson, P. (1987) Journal of Physics D: Applied Physics, 20, 635. http://dx.doi.org/10.1088/0022-3727/20/5/011
- Jaya Ram, K. (1974) Zeitschrift für Physik, 271, 217. http://dx.doi.org/10.1007/BF01677926
- Airey, D.R. (1978) Proceedings of the 5th International Conference on Gas Discharges, Liverpool, September 1978, University of Liverpool.
- Devoto, R.S. (1967) Physics of Fluids, 10, 2105-2112. http://dx.doi.org/10.1063/1.1762005
- Andanson, P. and Cheminat, B. (1979) Revue de Physique Appliquée, 14, 775. http://dx.doi.org/10.1051/rphysap:01979001408077500
- Drellishak, K.S., Aeschliman, D.P. and Cambel, A.B. (1965) The Physics of Fluids, 9, 1590. http://dx.doi.org/10.1063/1.1761469
- Lochte-Holtgreven, W. and Richter J. (1995) Radiation of Hot Gases. In: P. Diagnostics, Ed., AIP Press, New York, 1-65.
- Liboff, R.L. (1959) The Physics of Fluids, 2, 40. http://dx.doi.org/10.1063/1.1724389
- Cybulski, R.J., RicMey, E.A. and Keller, T.A. (1962) Application of Liquid-Helium Cryopumping to Large Electric Rocket Vacuum Facilities. In: Preuss, L.E., Ed., Vacuum Symposium Transactions, Vol. 2, Macmillan GO, 1279-1284.
- Trajmar, S., Williams, W. and Strivastava, S.K. (1977) Journal of Physics B: Atomic and Molecular Physics, 10, 3323. http://dx.doi.org/10.1088/0022-3700/10/16/025
- Hirschfelder, J.O., Curtiss, C.F. and Bird, R.B. (1954) Molecular Theory of Gases and Liquids. Wiley, New York.
- Capitelli, M. and Devoto, R.S. (1973) Physics of Fluids, 16, 1835-1841. http://dx.doi.org/10.1063/1.1694222
- Capitelli, M., Celiberto, R., Gorse, C. and Giordano, D. (1995) Plasma Chemistry and Plasma Processing, 16, S269- S302. http://dx.doi.org/10.1007/BF01512639
- Devoto, R.S. (1973) Physics of Fluids, 16, 616. http://dx.doi.org/10.1063/1.1694396
- Mitchner, M. and Kruger, C.H. (1973) Partially Ionized Gases. Wiley, New York.
- Amry, A.M.A., Rasheedy, M.S., El-Koramy, R.A. and Turky, A.A. (1995) Japanese Journal of Applied Physics, 34, 3697-3702.
- Hermann, W. and Schade, I.E. (1970) Zeitschrift für Physik, 233, 333-350. http://dx.doi.org/10.1007/BF01397793
- Sakuta, T., Kito, Y. and Miyachi, I. (1980) IEEE Transactions on Plasma Science, 8, 29-32. http://dx.doi.org/10.1109/TPS.1980.4317261
- Vacquié, S., Rahhaoui, B. and Rahal, A.M. (1990) Journal of Applied Physics, 68, 3153.
- Vacquié, S. (1996) Pure and Applied Chemistry, 68, 1133-1136. http://dx.doi.org/10.1351/pac199668051133
- Chervy, B., Gleizes, A. and Razafinimanana, M. (1994) Journal of Physics D: Applied Physics, 27, 1193. http://dx.doi.org/10.1088/0022-3727/27/6/017
NOTES
*Corresponding author.






















