Received 10 December 2014; accepted 23 December 2014; published 14 January 2015

ABSTRACT

This paper posits an extra force field, “super force field”, as the short-distance additional force field to ordinary force fields (gravitational, weak, electromagnetic, and strong) at absolute zero or extremely high density. The short distance super force field accounts for quantum phase transition at absolute zero, and provides the basic cause of superconductivity above absolute zero by quantum fluctuation. At absolute zero or extremely high density, to prevent inactivation or singularity, respectively, the short-distance super force field emerges in between the core particle and the ordinary force field, resulting in the super ordinary force field. In the super ordinary force field, the short-distance super force field excludes the long-distance ordinary force field. At absolute zero, the super ordinary force field emerges to account for quantum phase transition at absolute zero. Through quantum fluctuation, the super ordinary force appears above absolute zero as in superconductivity. Through quantum fluctuation, superconducting electric current is “super current” as one giant quantum state with the super force field that does not interact with ordinary forces, resulting in zero resistance.

Keywords:

Superconductivity, Digital Space, Quantum Mechanics, Uncertainty Principle, Super Force Field, Quantum Phase Transition, Quantum Fluctuation, Superconductor, Cooper Pairs

1. Introduction

Superconductivity is characterized by zero electrical resistance and exclusion of magnetic fields below a characteristic critical temperature, T_c. The cause of superconductivity is not completely clear. The conventional model of superconductivity is the BCS theory [1] . It consists of Cooper pair as a bound pair of electrons, each having equal but opposite spin and angular momentum. In the BCS theory, the Cooper pairs travel freely through a superconductor, but outside of the Cooper pairs, many interactions can disrupt and destroy the Cooper pairs. To avoid this dilemma, the BCS theory assumes, for some unknown cause, that below T_c. superconductivity involves only the interaction in the Cooper pairs without involving any interactions outside of the Cooper pairs. In quantum mechanics, this assumption of the exclusion of the interactions outside of the Cooper pairs is possible only if a whole superconductor consisting of the Cooper pairs becomes one giant quantum state, like a giant molecule without obstruction for electron flow, resulting in zero electrical resistance. There is no indication that a whole superconductor is one ordinary giant quantum state, like a giant molecule. The assumption of the exclusion of the interactions outside of the Cooper pairs remains unexplained in the BCS theory. Another unexplained phenomenon is quantum phase transition, a phase transition between different quantum phases of matter at absolute zero. It is not clear exactly what quantum phase of matter is at absolute zero.

This paper posits an extra force field, “super force field”, as the short-distance additional force field to ordinary force fields (gravitational, weak, electromagnetic, and strong) at absolute zero or extremely high density. In the super force field model, the quantum phase of matter at absolute zero is simply a force field related to the super force field. Through quantum fluctuation, the super force field appears above absolute zero as in superconductivity. Through quantum fluctuation, superconducting electric current consisting of Cooper pairs is simply “super current” as one special giant quantum state with the super force field that excludes ordinary interactions outside of the Cooper pairs, resulting in zero electric resistance. The basic cause of superconductivity, therefore, is the short-distance super force field.

The short-distance super force field is derived from the digital space structure [2] -[4] . In the conventional space structure, space is homogeneous. In the digital space structure, space can be homogeneous or heterogeneous, and is digitalized by 1 and 0 for attachment space and detachment space, respectively. Attachment space denoted as 1 allows object to attach to account for rest mass and reversible movement, while detachment space denoted as 0 allows no object to attach to account for irreversible kinetic energy. Different combinations of attachment space (as 1) and detachment space (as 0) result in different physical phenomena. The conventional space structure cannot explain clearly the important phenomena, such as the differences in measurement between quantum mechanics and special relativity, the origin of superconductivity, and singularity in black hole. These phenomena can be derived directly by the different combinations of 1 and 0 in the digital space structure. An extra force field (the short-distance the super force field) can be derived from the digital space structure to generate superconductor to exclude ordinary force fields and superstar to replace black hole [5] .

Section 2 deals with the digital space structure. The super force field is described in Section 3. Quantum phase transition related to the super force field at absolute zero is described in Section 4. Section 5 deals with superconductivity related to the quantum fluctuation of the super force field.

2. The Digital Space Structure

The digital space structure [2] - [4] consists of attachment space (denoted as 1) and detachment space (denoted as 0). Attachment space attaches to object permanently or reversibly. Detachment space detaches from the object at the speed of light. Attachment space relates to rest mass and reversible movement, while detachment space relates to irreversible kinetic energy. Different stages of our universe have different space structures [6] .

The transformation between mass (massive particle) in attachment space and kinetic energy (massless particle) in detachment space is through the scalar Goldstone boson. For example, massive particles with n units of attachment space, denoted as (1)_n, are converted into massless particles with n units of detachment space, denoted as (0)_n through the Goldstone bosons. The addition of the Goldstone bosons to massless particles in detachment space results in massive particles in attachment space, while the removal of removal of the Goldstone bosons in attachment space leads to massless particles in detachment space.

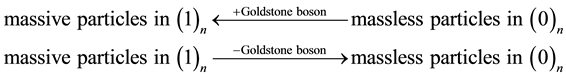(1)

The Goldstone boson provides the longitudinal degree of freedom for massive particle in attachment space. The Goldstone boson itself is a zero-energy virtual particle by taking energy from and returning energy to the object transformed by the Goldstone boson. The Goldstone boson in the Standard Model for electroweak interaction is the Higgs boson [7] .

The combination of attachment space (as 1) and detachment space (as 0) brings about three different space structures: binary partition space, miscible space, or binary lattice space as below.

(2)

Binary partition space, (1)_n(0)_n, consists of two separated continuous phases of multiple quantized units of attachment space and detachment space. In miscible space, attachment space is miscible to detachment space, and there is no separation of attachment space and detachment space. Binary lattice space, (1 0)_n, consists of repetitive units of alternative attachment space and detachment space.

Binary partition space is the space for wavefunction in quantum mechanics. In wavefunction,

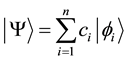(3)

Each individual basis element, 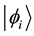, attaches to attachment space, and detach from the adjacent basic elements by detachment space. In binary partition space, a basic element contains both attachment space and detachment space. Neither attachment space nor detachment space is zero in binary partition space for a basic element. The measurement in the uncertainty principle in quantum mechanics is essentially the measurement of attachment space and momentum in binary partition space: large momentum has small non-zero attachment space, while large attachment space has low non-zero momentum. In binary partition space, an entity is both in constant motions as wave for detachment space and in stationary state as a particle for attachment space, resulting in the wave-particle duality.

Detachment space contains no object that carries information. Without information, detachment space is outside of the realm of causality. Without causality, distance (space) and time do not matter to detachment space, resulting in non-localizable and non-countable space-time. The requirement for the system (binary partition space) containing non-localizable and non-countable detachment space is the absence of net information by any change in the space-time of detachment space. All changes have to be coordinated to result in zero net infor- mation. This coordinated non-localized binary partition space corresponds to nilpotent space. All changes in energy, momentum, mass, time, space have to result in zero as defined by the generalized nilpotent Dirac equation by B. M. Diaz and P. Rowlands [8] .

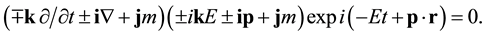(4)

where E, p, m, t and r are respectively energy, momentum, mass, time, space and the symbols ±1, ±i, ±i, ±j, ±k, ±i, ±j, ±k, are used to represent the respective units required by the scalar, pseudoscalar, quaternion and multivariate vector groups. The changes involve the sequential iterative path from nothing (nilpotent) through conjugation, complexification, and dimensionalization. The non-local property of binary partition space for wavefunction provides the violation of Bell inequalities [9] in quantum mechanics in terms of faster-than-light influence and indefinite property before measurement. The non-locality in Bell inequalities does not result in net new information.

In binary partition space, for every detachment space, there is its corresponding adjacent attachment space. Thus, no part of the object can be irreversibly separated from binary partition space, and no part of a different object can be incorporated in binary partition space. Binary partition space represents coherence as wavefunction. Binary partition space is for coherent system. Any destruction of the coherence by the addition of a different object to the object causes the collapse of binary partition space into miscible space. The collapse is a phase transition from binary partition space to miscible space.

(5)

Another way to convert binary partition space into miscible space is gravity. Penrose [10] pointed out that the gravity of a small object is not strong enough to pull different states into one location. On the other hand, the gravity of large object pulls different quantum states into one location to become miscible space. Therefore, a small object without outside interference is always in binary partition space, while a large object is never in binary partition space.

The information in miscible space is contributed by the miscible combination of both attachment space and detachment space, so information can no longer be non-localized. Any value in miscible space is definite. All observations in terms of measurements bring about the collapse of wavefunction, resulting in miscible space that leads to eigenvalue as definite quantized value. Such collapse corresponds to the appearance of eigenvalue, E, by a measurement operator, H, on a wavefunction, Y.

(6)

In miscible space, attachment space is miscible to detachment space, and there is no separation of attachment space and detachment space. In miscible space, attachment space contributes zero speed, while detachment space contributes the speed of light. A massless particle, such as photon, is on detachment space continuously, and detaches from its own space continuously. For a moving massive particle consisting of a rest massive part and a massless part, the massive part with rest mass, m₀, is in attachment space, and the massless part with kinetic energy, K, is in detachment space. The combination of the massive part in attachment space and massless part in detachment leads to the propagation speed in between zero and the speed of light. To maintain the speed of light constant for a moving particle, the time (t) in moving particle has to be dilated, and the length (L) has to be contracted relative to the rest frame.

(7)

where is the Lorentz factor for time dilation, and length contraction, E is the total energy,

and K is the kinetic energy.

As described in Reference [6] , before the beginning of our current universe, the universe contained only attachment space, and at the beginning of the current universe, the 10d particle universe was sliced into six particles: 9d, 8d, 7d, 6d, 5d, and 4d equally by mass. Detachment space (0) involves in the slicing of dimensions. Attachment space is denoted as 1. For example, the slicing of 10d particles into 4d particles is as follows.

(8)

where m is for the number of units of core particles, n is for the number of units of force fields, and k is number of types of force fields. The two products of the slicing are the 4d-core attachment space for core particle and 6 types of 4d quantized units for the ordinary force fields. The 4d core attachment space surrounded by 6 types of many (n) 4d-quantized units corresponds to the core particle surrounded by 6 types of many small 4d particles. The ordinary force fields are the force fields in binary lattice space.

3. The Super Force Field

The uncertainty principle is applicable to binary partition space (1)_n(0)_n. The uncertainty principle for quantum mechanics is expressed as follows.

(9)

The position, x, and momentum, p, of a particle cannot be simultaneously measured with arbitrarily high precision. The uncertainty principle requires every physical system to have a zero-point energy (non-zero minimum momentum) and to have a non-zero minimum wavelength as the Planck length. In terms of the space structure, detachment space relating to kinetic energy as momentum is σ_p, and attachment space relating to space (wavelength) for a particle is σ_x. Neither detachment space nor attachment space is zero in the uncertainty principle, and detachment space is inversely proportional to attachment space. Quantum mechanics for a particle follows the uncertainty principle.

The uncertainty principle is applicable only to continuous detachment space. The n units of detachment space in binary lattice space (10)_n are separated, so the uncertainty principle is not applicable to binary lattice space. As a result, particles in binary partition space follow the uncertainty principle, while the ordinary force fields (electromagnetic, strong, weak, and gravitational force fields) in binary lattice space follow the certainty principle, (Particles follow quantum mechanics with the uncertainty principle, while ordinary force fields without occupied particles follow classical mechanics without the uncertainty principle.) For ordinary force field at absolute zero with infinitesimal movement, all detachment space (momentum) in binary lattice space virtually ceases to exist, so the binary lattice space as the force field collapses into infinite attachment space (wavelength) with infinitesimal momentum, resulting in the inactivation of force field. At extremely high density to produce infinite interacting energy (infinite momentum) from the interaction among particles at infinitesimal distances, all attachment space (rest mass) in the binary lattice space virtually ceases to exist, so the binary lattice space as the force field collapses into infinite detachment space (momentum) with infinitesimal wavelength, resulting in singularity as infinite interacting energy.

In the generalized uncertainty principle [11] , an extra term related to the Planck energy is introduced to avoid singularity.

(10)

where α is a constant and G relates to the Planck energy, At energy much below the Planck energy, the extra term in Equation (10) is irrelevant and the Heisenberg uncertainty principle is recovered, while approaching the Planck energy, the extra term becomes relevant, and is related to the minimal observable length. In this paper, an extra force field is introduced to maintain the non-zero minimal length and momentum at the extreme conditions. This extra force field is “the super force field” in binary partition space that follows the uncertainty principle. The super force fields with non-zero minimum momentum and wavelength emerge in between particles and their the ordinary force fields (electromagnetic, strong, weak, and gravitational force fields) to prevent the inactivation of force fields at absolute zero and singularity at extremely high density in the ordinary force fields as follows.

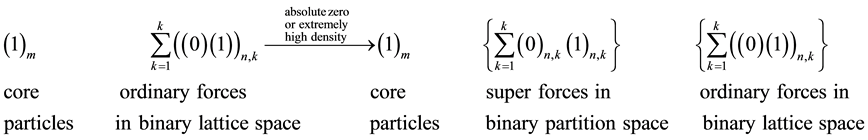
where m is for the number of units of core particles, n is for the number of units of force fields, and k is number of types of force fields. The super force field has only one orbital, so the super force field is a short-distance force field, while the ordinary force fields have many separated orbitals, so the ordinary force fields are long- distance force fields. The short-distance super force field and the long-distance ordinary force fields coexist as the super ordinary force field. The super ordinary force field as a whole entity avoids inactivation and singularity at the extreme conditions.

At extremely high density, the super ordinary force field produces singularity-free superstar [5] instead of black hole with singularity. A singularity-free superstar results from the collapse of a large star. Gammaray burst (GRB) generated during this process of collapse is in good agreement with the observation of GRB. At absolute zero, quantum phase transition produces the super ordinary force field as discussed in Section 4, and the quantum fluctuation of the super ordinary force field generates superconductivity as discussed in Section 5.

4. Quantum Phase Transition

In the conventional model, a quantum phase transition (QPT) is a phase transition between different quantum phases of matter at absolute zero [12] . In the super force field model, quantum phase transition corresponds to super phase transition (SPT) as the phase transition between ordinary force field and the super ordinary force field at absolute zero. In the super ordinary force field, the short-distance super force field and the long-distance ordinary force field are separated, and the super force field excludes the ordinary force field. As a result, no long-distance ordinary force field exists in the short-distance super force field. For examples, under super phase transition, orderly ferromagnetism with ordinary magnetism is transformed into disorderly paramagnetism resulted from the exclusion of ordinary magnetism by the super force field in short-distance.

The distance of the super force field for individual particles is very short. The emergence of the detectable super force field requires the dense system of a large number of correlated (strongly interacted) particles, typically electrons, with the super force field. The combination of the distances of the super force fields among correlated electrons in a dense-correlated electron system [13] allows the emergence of the detectable super force field. As a result, the super force field has the property of emergence [14] as a process whereby the super force field arises through interactions among electrons in a dense-correlated electron system. For example, a highly dense Einstein-Bose condensate, such as Helium-4, undergoes quantum phase transition. The inducer to form the dense-correlated electron system for the emergence of the super force field is “super inducer” corresponding to quantum phase transition inducer in the conventional model. The common quantum phase transition inducers include pressure [15] , magnetic field [16] , and doping [17] . In the conventional model, the quantum phase transition is driven by quantum phase transition inducer, and quantum critical point (QCP) is the critical (g_c) strength or amount of a quantum phase transition inducer to attain quantum phase transition at absolute zero. In the super force field model, quantum phase transition inducer corresponds to super inducer, and quantum critical point corresponds to super critical point (SCP).

To have super phase transition above absolute zero requires quantum fluctuation through Heisenberg’s uncertainty principle. In the conventional model, quantum critical point can be extended from absolute zero to the temperature above absolute zero through quantum fluctuation, and such extended quantum critical point is called quantum criticality [18] . In the super force field model, quantum criticality corresponds to super criticality. The extended super ordinary force field appears above absolute zero through quantum fluctuation. Super phase transition and super criticality are shown in Figure 1.

5. Superconductivity

Superconductivity is characterized by zero electrical resistance and exclusion of magnetic fields below a characteristic critical temperature, T_c. In a superconductor, the resistance drops abruptly to zero at T_c. An electric current flows through a loop of superconducting wire indefinitely with no power source. In the super force field model, superconducting electric current is in the short-distance super force field that excludes ordinary force fields. Without interacting with ordinary force fields in short distance, superconducting electric current does not have electrical resistance.

The emergence of the super force field in electric current occurs in the dense-correlated electron systems that involve quasiparticle fluctuations in terms of the fluctuations between the absorption and emission of quasiparticles. Quasiparticles include phonon and magnon (spin wave) [19] for low temperature superconductor and high temperature superconductor, respectively. A phonon is a collective excitation of the crystal lattice atoms or ions, while a magnon is a collective excitation of the electrons’ spin structure in a crystal lattice. During the formation of superconductivity, passing electrons absorb and emit quasiparticles continuously by lattice vibration or antiferromagnetic spin fluctuation. The continuous quasiparticle fluctuation between absorption and emission results in virtual quasiparticles. The quantum fluctuation of virtual quasiparticles transforms virtual quasiparticle in ordinary force field to virtual super quasiparticle in the super ordinary force field, and transforms passing electrons

into super bound electrons bound by virtual super quasiparticles. Super bound electrons correspond to conventional Cooper pairsas shown in Figure 2.

At the critical temperature T_c, the overlapping of super virtual quasiparticles around the passing super bound electrons constitutes the anisotropic “super density wave” corresponding to conventional charged or spin density wave for the whole material. Super density wave excludes external ordinary forces such as repulsive Coulomb force, resulting in superconducting electric current without electrical resistance. Superconducting electric current is “super current” as one giant quantum state with the super force field that does not interact with ordinary forces, resulting in zero resistance. T_c is proportional to the binding energy from virtual super quasiparticle connecting super bound electrons, because heat can break the bonds in super density wave. To have superconductivity for a whole material, the super density wave has to be total instead of partial for the whole material. The partial super density wave competes with the total super density wave. At T_c and below T_c, the total super density wave dominates the partial density wave by redirecting the electrons from the partial super density wave to the total super density wave [20] . The partial super density wave corresponds to incommensurate fluctuations in pseudogap.

The super ordinary force field as the coexistence of the short-distance super force and the long-distance ordinary force in the super ordinary force corresponds the conventional Hubbard model [21] . In the Hamiltonian of the Hubbard model, there is a coexistence of a kinetic term allowing for tunneling (“hopping”) of particles between sites of the lattice and a potential term U consisting of an on-site Coulomb repulsion.

(11)

where represents short-distance nearest-neighbor interaction on the lattice. The kinetic term corresponds to the short-distance super force, and U corresponds to the long-distance ordinary force. As in the short-distance super force, electron hopping can only take place between nearest-neighbor sites, and all hopping processes have the same kinetic energy, −t. The binding of electrons results in an electronic band structure. The super force in super ordinary force is responsible for superconductivity. The Hubbard model produces both a metallic state and an insulating state, depending on the values of ?t and U.

The standard theory for the conventional low temperature conductivity is the BCS theory [1] . According to the theory, as one negatively charged electron passes by the positively charged ions in the lattice of the superconductor, the lattice distorts. This in turn causes phonons to be emitted to form a channel of positive charges around the electron. The second electron is drawn into the channel. Two electrons link up to form the “Cooper pair” without the normal repulsion.

In the super force field model of the low temperature superconductor, a virtual super phonon is the link for electrons. In the super force field model, as an electron passes the lattice, lattice atom absorbs the energy of the passing electron to cause a lattice bond to stretch or to contract. When the lattice bond recoils to normal position, the lattice atom emits a phonon, which is absorbed by the next passing electron. The electron then emits the phonon, which is absorbed by the next lattice atom to cause its bond to stretch. When the lattice bond recoils to normal position, the lattice atom emits a phonon, which is absorbed by the next passing electron. This process of

the continuous absorption and emission of phonons by the nearest passing electrons and the nearest sites in lattice brings about virtual phonons in ordinary force field. The quantum fluctuation of virtual phonons transforms virtual phonons in ordinary force field into virtual super phonons in the super ordinary force field, and transforms passing electrons into passing super bound electrons, corresponding to conventional Cooper pairs. At the critical temperature T_c above absolute zero, the overlapping of virtual super phonons around the passing super bound electrons constitutes the anisotropic super density wave with a s-orbital structure corresponding to conventional charged density wave that excludes external ordinary forces such as repulsive Coulomb force, resulting in superconductor without electrical resistance. Lattices in low temperature superconductors have simple structures, containing no subsystem that has partial super wave. As a result, there is no incommensurate charged density wave for pseudogap in low temperature superconductors.

The super force field in superconductor repels magnetism as in the Meissner effect. The energy (stiffness) of the super force field can be determined by the penetration of boson force field into the super force field as expressed by the London equation for the Meissner effect.

(12)

where H is an external boson field and λ is the depth of the penetration of magnetism into super force field shell. This equation indicates that the external boson field decays exponentially as it penetrate into the super force field. The super bond energy (E_l) in super bond connecting super bound electrons is two times the energy gap D_t of a super bound electron at T_c.

(13)

The elimination of superconductivity is to break the super bonds of super bound electrons.

The super force field is a confined short distant force field, so the neighboring super phonons have to be close together. To have a continuous super lattice without gaps, it is necessary to have sufficient density of the vibrating lattice atoms. Thus, there is critical density, D_c, of vibrating lattice atoms. Below D_c, no super lattice can be formed. In a good conductor, an electron hardly interacts with lattice atoms to generate lattice vibration, so a good conductor whose density for vibrating lattice atoms below D_c does not become a superconductor. T_c is directly proportional to the density of vibrating lattice atoms and the frequency of the vibration (related to the isotope mass). The “gap” in super lattice is the area without vibrating lattice atoms. The gap allows electrical resistance. Superconductor has “perfect super lattice” without significant gap, while “imperfect super lattice” has significant gap to prevent the occurrence of superconductivity.

High temperature superconductor that has a much higher T_c than low temperature superconductor is derived from magnon fluctuation through antiferromagnetic spin fluctuation. All high temperature superconductors involve the particular type of insulator with various kinds of dopants. A typical insulator is Mott insulator, such as copper oxides, CuO₂. CuO₂ forms a two-dimensional layer, with the Cu atoms forming a square lattice and O atoms between each nearest-neighbor pair of Cu atoms. In the undoped CuO₂, all of the planar coppers are in the Cu²⁺ state, with one unpaired electron per site. Two neighboring unpaired electrons with antiparallel spins have lower ground energy than two neighboring unpaired electrons with parallel spins. Consequently, CuO₂ layer consists of the antiparallel spin pairs, resulting in antiferromagnetism. The insulating character of this state is thought to result, not from the antiferromagnetism directly, but from the strong on-site Coulomb repulsion, which is the energy cost of putting an extra electron on a Cu atom to make Cu⁺. This Coulomb energy for double occupancy suppresses conduction.

La_xSr_xCu₂O₄ is an example of high temperature conductor. The key ingredient consists of CuO₂ layers. The doping of Sr provides chemical environment to shift the charge away from the CuO₂ layers, leaving “doping holes” in the CuO₂ layers. The shifting of electrons allows the occurrence of electric current. When an antiparallel spin pair loses an electron by doping, a doping hole is in the spin pair. In the super force field model, the adjacent passing electron outside of the pair fills in the hole. The filled-in passing electron has a parallel spin as the electron in the original pair. Parallel spin pair has higher ground state energy than antiparallel pair, so the filled-in electron absorbs a magnon to gain enough energy to undergo a spin change. The result is the formation of an antiparallel spin pair. The antiparallel spin pair has lower ground state energy than an antiparallel spin pair, so it emits a magnon. The next passing electron absorbs the magnon, undergoes a spin change, and repeats the process. The process is the continuous spin fluctuation with continuous absorption and emission of magnons [22] [23] . This process of the absorption and emission of magnons by the nearest passing electrons brings about virtual magnons in ordinary force field. The quantum fluctuation of virtual magnons transforms virtual magnons in ordinary force field into virtual super magnons in the super ordinary force field, and transforms passing electrons into passing super bound electrons, corresponding to conventional Cooper pairs. At T_c above absolute zero, the overlapping of virtual super magnons around passing super bound electrons constitutes the anisotropic super density wave with a d-orbital structure corresponding to conventional spin density wave that excludes external ordinary forces such as repulsive Coulomb force, resulting in superconductor without electrical resistance. The binding energy of super bound electrons from spin fluctuation is higher than that from lattice vibration, so T_c for high temperature superconductor based on the spin fluctuation is higher than T_c for low temperature superconductor based on lattice vibration.

Materials in high temperature superconductors have complex structures. The partial super density waves compete with the total super density waves. As a result, there are incommensurate super density waves for pseudogap in high temperature superconductors. Lee and Davis propose that antiferromagnetic spin fluctuation is the universal cause not only for superconductivity but also for all the observed incommensurate spin density wave fluctuation in pseudogaps [24] . The differences in superconductivity and pseudogaps in different materials are derived from the varying energy levels of the electrons that are free to carry current on the Fermi surface as in the following effective Hamiltonian,

(14)

The first term is about the Fermi surface and the second term is about antiferromagnetic spin fluctuation. In the equation, k and s are the momentum and the spin labels, respectively. S_i represents the total spin operator in the ith unit cell. is a sum restricted to the neighborhood of the Fermi surface, ε(k) is the dispersion of the relevant band in the vicinity of the Fermi surface, and should be understood as a electron-electron scattering term. One example of the competitive partial super density wave and the total super density wave is observed and calculated by Hayward, Hawthorn, Melko, and Sachdev [20] . The experiments observe that as the temperature decreases, incommensurate density wave fluctuations whose strength rises gradually over a wide temperature range above T_c, but then decreases as the temperature is lowered below T_c.

The super force field is derived from the digital space structure where space is digitalized by 1 and 0 for attachment space and detachment space, respectively. Attachment space allows object to attach to account for rest mass, while detachment space allows no object to attach to account for kinetic energy. The combination of attachment space and detachment space brings about the three structures: binary partition space, miscible space, and binary lattice space. Binary partition space (1)_n(0)_n accounts for quantum mechanics of particle-wave and the super force field. In miscible space (1+0)_n, attachment space is miscible to detachment space without separation to account for special relativity. Binary lattice space (1 0)_n accounts for ordinary force fields. The uncertainty principle with non-zero minimum momentum and wavelength is applicable only to binary partition space, not binary lattice space. As a result, ordinary force fields without non-zero minimum momentum and wavelength become inactivated at absolute zero, and singularity at extremely high density. To prevent inactivation and singularity, the super force field in binary partition space emerges in between the core particle and the ordinary force field, resulting in the super ordinary force field at the extreme conditions. In the super ordinary force field, the short-distance super force field excludes the long-distance ordinary force field. At absolute zero, quantum phase transition is the transition between ordinary force and the super ordinary force.

Through quantum fluctuation, the super ordinary force field appears above absolute zero. Superconducting electric current becomes the supper current that excludes ordinary force fields. Without interacting with ordinary force fields, superconducting electric current does not have electrical resistance. The emergence of the super force field in electric current occurs in the dense-correlated electron systems that involve quasiparticle fluctuations in terms of the fluctuations between the absorption and emission of quasiparticles, including phonon and magnon for low temperature superconductor and high temperature superconductor, respectively. The result is the formation of virtual quasiparticles. The quantum fluctuation of virtual quasiparticles brings about virtual super quasiparticles in the super force field, and the binding of passing electrons with virtual super quasiparticles results in superconducting electric current that is super current as one giant quantum state with the super force field. Table 1 shows the comparison between the super force model and the conventional model for superconductivity.

6. Conclusion

This paper posits an extra force field, “super force field”, as the short-distance additional force field to ordinary force fields (gravitational, weak, electromagnetic, and strong) at absolute zero or extremely high density. The short distance super force field accounts for quantum phase transition at absolute zero, and provides the basic cause of superconductivity above absolute zero by quantum fluctuation. At absolute zero or extremely high density, to prevent inactivation or singularity, respectively, the short-distance super force field emerges in between the core particle and the ordinary force field, resulting in the super ordinary force field. In the super ordinary force field, the short-distance super force field excludes the long-distance ordinary force field. At extremely high density, the super ordinary force field produces singularity-free superstar [5] instead of black hole with singularity. As a result, the super force field solves the problem of singularity in physics. At absolute zero, the super ordinary force field emerges to account for quantum phase transition at absolute zero. Through quantum fluctuation, the super ordinary force appears above absolute zero as in superconductivity. Through quantum fluctuation, superconducting electric current is “super current” as one giant quantum state with the super force field that does not interact with ordinary forces, resulting in zero resistance.

References