Received 4 September 2014; revised 1 October 2014; accepted 25 October 2014

ABSTRACT

The De Broglie’s approach to the quantum theory, when combined with the conservation rule of momentum, allows one to calculate the velocity of the electron transition from a quantum state n to its neighbouring state as a function of n. The paper shows, for the case of the harmonic oscillator taken as an example, that the De Broglie’s dependence of the transition velocity on n is equal to the n-dependence of that velocity calculated with the aid of the uncertainty principle for the energy and time. In the next step the minimal distance parameter provided by the uncertainty principle is applied in calculating the magnetic moment of the electron which effectuates its orbital motion in the magnetic field. This application gives readily the electron spin magnetic moment as well as the quantum of the magnetic flux known in superconductors as its result.

Keywords:

Velocity of the Electron Transitions between Quantum Levels, De Broglie Wave Packets, Magnetic Moment of the Electron Spin, Quantum of the Magnetic Flux, The Uncertainty Principle for Energy and Time

1. Introduction

The paper has as its aim to approach two rather different problems, both on the basis of the uncertainty principle for energy and time. The first is connected with the speed of transition between two different (neighbouring) quantum levels of the harmonic oscillator. The approach is based on the fact that in the oscillator case a space difference characteristic for two quantum levels can be easily calculated on a semiclassical footing, so in order to obtain the speed of transition only the corresponding time interval is required. This interval is provided by the uncertainty principle which couples 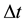with the corresponding energy change. The result obtained for the seeked velocity of transition is in a satisfactory agreement with a corresponding difference of the De Broglie velocities connected with the same transition.

The second problem is directed to the calculation of the electron magnetic moment. Classically this moment is an effect of the angular momentum of the electron particle moving along the orbit induced by the magnetic field. In fact the magnetic moment differs from the angular momentum only by a constant multiplier. But the uncertainty principle provides us with the result that not every size of parameters describing the classical particle motion in the magnetic field is acceptable. First the minimal intervals in space and time which should not be violated in course of the motion are presented. An application of one of these intervals, namely the spatial one, to calculation of the magnetic moment of the orbiting electron gives readily the spin magnetic moment of that electron.

2. De Broglie’s Transition Velocity between the Quantum Levels and Its Alternative Calculation

Before the outspring of the wave mechanics the De Broglie’s velocities of the wave packets were applied in calculating the action function entering the Sommerfeld rule defining the quantum levels of the old quantum theory [1] -[5] . This calculation was represented by the formula:

(1)

Here is the rest mass of the electron, 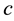is the speed of light, 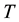is the time period of the moving body―say an oscillator―along a closed orbit, 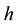is the Planck constant, is the velocity of the wave packet, 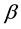is the ratio

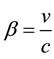(2)

and 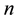is the index of a quantum state.

By neglecting the radical expression in the denominator of (1), which for small 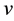is close to unity, we obtain in (1) the formula

(1a)

or

(3)

on condition we put

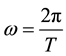(4)

for the expression of the circular frequency, and

(5)

Formula (3) is an expression for the double kinetic energy of the harmonic oscillator calculated at position where the oscillator potential energy is zero, so the oscillator has only its velocity. For a linear oscillator having momentum a full expression for energy is

(6)

therefore a situation of the vanishing potential energy in (6) is attained at

(7)

An advantage of the De Broglie’s treatment is that it applies the notion of the wave packet velocity which can be next identified with the speed of a particle, for example an electron particle; see e.g. [6] .

In general the velocity observable in quantum systems is seldom discussed, though it can be of use when the electron transition between two quantum states takes place. A difficulty in calculating the transition speed between two quantum states is due to the fact that in principle we have no suitable formalism to that purpose. For example, in the framework of the old quantum theory, we can rather easily define the position change, say

(8)

of some special point of a system having the space coordinate, when this change is connected with the change of a quantum state, but a stumbling block is to calculate the time interval

(9)

associated with the interval (8). For an oscillator an easily accessible change of is the change of the oscillator amplitude

(10)

due to the change of the quantum state n of the oscillator. The amplitude (10) is readily obtained from (6) because at the turning points of the oscillator we have

(11)

so

(12)

Here is the oscillator energy in state:

(6a)

This formula is simplified to that applied in the old quantum theory, so the quantum-mechanical correction 1/2 to is neglected.

The first aim of the present paper is to calculate on the basis of the uncertainty principle which couples the energy change due to an electron transition with the transition time interval (9). The principle is represented by the formula [7] - [10]

(13)

which―in calculating―is approximated by

(13a)

The accuracy of (13a) increases as much as the speed of the examined transition approaches the velocity. The aim of the first part of the paper is to compare the transition velocity obtained from the uncertainty principle with that derived with the aid of the formalism given by De Broglie.

3. Speed of Transitions between Quantum States Calculated on the Basis of (1a) and (13a)

For an individual quantum state the Formula (1a) gives

(14)

so for we have

(14a)

The central oscillator point (7) in which only the kinetic energy does not vanish repeats for all quantum states, but the oscillator velocities will differ at that point according to (14) [we neglect here the result that in fact (3) gives a double kinetic energy at point (7)]. Since the motion across (7) is performed along the same direction for all, it is natural to assume the conservation of momentum at that point. In effect the difference of between states and can be identified with the transition speed between and. Therefore we obtain for that speed the difference

(15)

The approximation entering the last steps of (15) holds for large.

The formalism of calculating the transition speed on the basis of (13a) requires some more manipulations. The aim is to obtain the transition velocity in terms of the formula

(16)

where from (12) and (6a)

(17)

On the other hand, the interval calculated from the uncertainty principle expressed in (13a) is

(18)

because

(19)

In effect of (17) and (18), the transition velocity (16) between and becomes

(20)

The both formulae, (15) and (20), become identical on condition the constant is replaced by a half of the constant given in (14a).

The problem of the difference of transition speeds considered separately for the case of emission or absorption of energy is here neglected: in fact we can substitute only positive, or absolute, into (13a) in order to obtain real. Nevertheless a formal distinction between the emission and absorption of energy by the oscillator is possible; see Ref. [11] .

4. Discussion on the Speed of the Transition Wave

It can be noted that the square value of the speed entering (1a) is modified in (1) by the factor

(21)

Therefore in order to obtain with the aid of (21) roughly a full agreeement between the De Broglie velocity (15) and that of (20) we should solve the equation

(22)

Equations (2) and (22) give

(23)

which is equivalent to the bi-quadratic equation

(23a)

This gives

(23b)

or

(24)

from which and from (14a) we obtain the following requirement for the frequency:

(25)

5. Magnetic Moment of an Electron Moving on an Orbit in a Constant Magnetic Field and Its Value Attained at the Extremal (Minimal) Radius Size Supplied by the Principle of Uncertainty

In examining the uncertainty principle for energy and time [see (13a)] two parameters concerning respectively a minimal space distance between two particles

(26)

and a minimal time interval between two events

(27)

could be derived [10] . Similar parameters characteristic for the distance in space and time, equal respectively to

(26a)

and

(27a)

have been proposed at a time of the outspring of quantum mechanics [5] [12] - [14] . The Formula (26a) is better known as the Compton wave length of the electron (equal to cm) [6] . The (26a) and (27a) differ from (26) and (27) solely by the factor of.

The task undertaken in the present paper is to apply a minimal distance (26) to calculate the magnetic moment of an electron orbiting in a constant magnetic field. This moment is defined classically by the angular momentum of the particle multiplied by a constant factor [15]

(28)

Upon the action of a constant magnetic field having the induction any electron is assumed to perform a constant orbital motion along a circle having the radius

(29)

where is the electron velocity on the orbit (being transversal to the direction of the magnetic field) and

(30)

is the circular frequency of the motion. In the first step our task is to calculate a critical (maximal) value of at which the motion can be performed. This is obtained if we note that the orbital velocity cannot exceed c, so we have the upper limit

(31)

and the smallest orbital radius should be equal to (26). In this way we obtain from (29)-(31) combined with (26) the condition for the critical:

(32)

A solution of (32) yields

(33)

The next step is to calculate the electron angular momentum with the use of (26) and (33). For a circular orbit and this gives

(34)

A final step is to substitute the result of (34) into the expression for the electron magnetic moment. We obtain

(35)

The result in (35) is equal precisely to the magnetic moment of the electron considered as a spin magnetic moment; see [6] and [16] . A characteristic point is that no quantization process has been used in calculations: the result is based solely on the uncertainty principle (13a) and classical electrodynamics.

Let us note that obtained in (33) causes a critical circulation frequency of the size:

(36)

6. Remarks on the Spin Magnetic Moment

A rather natural step can be an application of the uncertainty principle to other kinds of matter than electrons. Here one has to be cautious because in the Formula (13a) ceases to be the electron mass. Another point is the calculation of: for example for the nuclear matter and its reactions the change of the mass should be taken into account [17] [18] .

For electrons, however, an application of the critical interval (26) can be done also in case of the electrostatics. This leads to a critical (maximal) strength of the electric field acting on an electron via the Coulomb interaction force:

(37)

For electrons the force obtained in this way is equal to only

(37a)

Both forces and [see (37) and (33)] depend strongly on. For example they increase dramati- cally with a substitution of the electron mass by the proton mass. On the other hand, the ratio of the forces (37) and (33) becomes a well-known constant

(38)

independent of the particle mass.

An interesting situation gives a coupling of the radius considered in (32) with the magnetic induction represented by. A product of the elementary planar surface

(39)

and in (33) gives

(40)

This is a quantum of the magnetic flux which is well-known in the theory of superconductors, see e.g. [19] .

7. Summary

In the paper two rather different effects have been examined in reference to the uncertainty principle for energy and time.

The first one concerns the change of speed of the De Broglie wave in case of transition from a quantum state to a neighbouring state. The transition speed obtained from the uncertainty principle has the same functional dependence on as the speed calculated from the De Broglie theory.

Another calculation considers the spin magnetic moment of the electron which in quantum mechanics is conventionally obtained in course of solving the Dirac’s equation; see e.g. [6] . We show that the same result for the spin magnetic moment can be attained by combining the uncertainty principle with the classical electromag- netic theory. Here a critical (minimal) length of the orbit radius derived from the uncertainty principle is combined with a critical (maximal) accessible strength of the magnetic induction. The parameter is calculated on the basis of electrodynamics supplemented by the relativistic theory.

A by-product of this calculation is a quantum of the magnetic flux well-known in the theory of super- conductors; see (40). It is obtained by multiplication of the induction entering (33) and elementary surface―due to the quantum distance (26)―represented in (39). This result implies that

(41)

from (33), as well as in (39), can be considered as the quanta of the magnetic induction and the surface area, respectively. A similar quantum concerning the intensity of the electric field can be obtained from (37):

(42)

The ratio of and provides us with the fine-structure constant (38) well known from the atomic theory; see e.g. [6] .

The semi-classical model of a spinning electron developed in the present paper is as follows. The electron is gyrating with a speed close to along a circular orbit of the radius defined by the distance (26) [see also (32)] which is derived from the uncertainty principle; see (13a) and [10] . The distance (26) is shorter by the factor of than the Compton length presented in (26a). It gives

(43)

which is shorter by many times than the first radius of the Bohr orbit in the hydrogen atom equal to 0.53 × 10⁻⁸ cm, but larger―also by many times―than the classical radius of the electron particle equal to [15] :

(44)

The circulation of the spinning electron is corresponding to the presence of the magnetic field in (41) and has the frequency (36) equal to about.

The magnetic moment obtained due to the circulation is equal to the Bohr magneton [see (35)]. The lowering of the magnetic interaction energy being an effect of creation of a spinning electron system is

(45)

References