Journal of Modern Physics
Vol.05 No.17(2014), Article ID:51735,6 pages
10.4236/jmp.2014.517183
Presence of Multifractality in High-Energy Nuclear Collisions
M. I. Haque1, M. Tariq2, Tahir Hussain3
1Department of Kulliyat, AK Tibbiya College, Aligarh Muslim University, Aligarh, India
2Department of Physics, Aligarh Muslim University, Aligarh, India
3Department of Applied Physics, Aligarh Muslim University, Aligarh, India
Email: mihaqueamu@gmail.com, mtariqamu@gmail.com, tahir.phys@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 September 2014; revised 25 September 2014; accepted 13 October 2014
ABSTRACT
In the present study an attempt is made to examine multifractality in multiparticle production in relativistic nuclear collisions; multifractality is investigated in 14.5 A GeV/c 28Si-nucleus collisions. For this, Gq-moments are calculated and variations of  with
with  are looked into. Values of mass exponents, tq, and generalised dimensions, Dq, are obtained. Analysis of multifractal moments reveals that multiplicity fluctuations are of dynamical nature.
are looked into. Values of mass exponents, tq, and generalised dimensions, Dq, are obtained. Analysis of multifractal moments reveals that multiplicity fluctuations are of dynamical nature.
Keywords:
Multifractal Moments, Dynamical Fluctuations, Quark-Gluon Plasma, Emulsion

1. Introduction
Analysis of high-energy heavy-ion collisions [1] -[4] offers a unique opportunity to investigate occurrence of dynamical fluctuations [5] - [7] in A-A collisions. To understand the real dynamics of multiparticle production, multifractality is envisaged to become an important tool for both theoretician and experimentalist. Intermittency and multifractality in turbulent fluids have been extensively studied [8] . It was suggested that multifractal analysis is carried out by calculating multifractal moments, 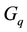 , of the multiplicity distributions in a given pseudorapidity
, of the multiplicity distributions in a given pseudorapidity  space. The main purpose of adopting multifractal moments,
space. The main purpose of adopting multifractal moments, 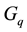 , approach is to explain multifractality and self-similarity in multiparticle production in relativistic nucleus-nucleus collisions. However,
, approach is to explain multifractality and self-similarity in multiparticle production in relativistic nucleus-nucleus collisions. However, 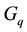 - moments are greatly influenced by statistical fluctuations in the case of events having lower multiplicities. It is worth mentioning that if the particle production process exhibits self-similar behavior, a modified form of
- moments are greatly influenced by statistical fluctuations in the case of events having lower multiplicities. It is worth mentioning that if the particle production process exhibits self-similar behavior, a modified form of 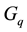 - moment is used by introducing a step function [2] , which leads to power-law dependence on the phase space bin size. Importance of multifractal analysis of high-energy nuclear collision data lies in the fact that these moments can be calculated for the negative values of the order of moments,
- moment is used by introducing a step function [2] , which leads to power-law dependence on the phase space bin size. Importance of multifractal analysis of high-energy nuclear collision data lies in the fact that these moments can be calculated for the negative values of the order of moments, 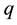 , also, whereas factorial moments are defined only for positive integral values of the order of moments. High-energy heavy-ion collisions are considered to be an ideal site for creating the conditions for producing Quark-Gluon Plasma (QGP) and dynamical fluctuations are one of the most reliable signals of QGP formation. Fluctuations in multiplicity and pseudorapidity distributions [9] are the most significant approaches to study nuclear matter produced in these collisions. Using the calculated values of various moments, non-statistical fluctuations in high-energy nuclear interactions can be investigated. It may be noted that multifractality may play an important role for searching the existence of dynamical fluctuations in the multipaticle production.
, also, whereas factorial moments are defined only for positive integral values of the order of moments. High-energy heavy-ion collisions are considered to be an ideal site for creating the conditions for producing Quark-Gluon Plasma (QGP) and dynamical fluctuations are one of the most reliable signals of QGP formation. Fluctuations in multiplicity and pseudorapidity distributions [9] are the most significant approaches to study nuclear matter produced in these collisions. Using the calculated values of various moments, non-statistical fluctuations in high-energy nuclear interactions can be investigated. It may be noted that multifractality may play an important role for searching the existence of dynamical fluctuations in the multipaticle production.
2. Mathematical Formalism
In order to study multifractality, a selected pseudorapidity interval,  is partitioned into
is partitioned into  bins of equal size
bins of equal size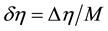 . Let
. Let  be the number of particles lying in
be the number of particles lying in 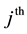 bin, then multifractal moments,
bin, then multifractal moments,  , may be calculated [1] [10] using:
, may be calculated [1] [10] using:
 (1)
(1)
where quantity  is defined as
is defined as 

In the above expression the summation is carried over non-empty bins only. For a given data sample, averaging is done over all the events comprising the total number of events, 


If rapidity distribution possesses fractal nature, a power-law behavior of 


where 
The resulting linear dependence of 



The generalized dimensions, 

Increase in the value of 


3. Experimental Details
We have analyzed data set comprising 555 events produced in 14.5 A GeV/c 28Si-nucleus collisions. Data sample include collisions with


4. Results and Discussion
4.1. Study of 
Figure 1 shows the variations of 









Figure 1. Variations of 

Figure 2. Variations of 

4.2. Mass Exponents
Values of the mass exponents, 












Figure 3 shows that the values of 





Figure 3. Variations of



Figure 4. Variations of 

FRITIOF generated data. It is noticed that the variations are similar for both the data sets. Again target dependence of the mass exponents, 



4.3. Generalized Dimensions
Figure 6 exhibits the variations of the generalized dimensions, 

Figure 5. Variations of mass exponents, 

Figure 6. Variations of generalized dimensions, 

5. Conclusion
The results of the present study are quite important for drawing meaningful conclusions regarding occurrence of multifractality in multiparticle production in high-energy nucleus-nucleus collisions. It is clearly observed that 





References
- Hwa, R.C. (1990) Physical Review D, 41, 1456. http://dx.doi.org/10.1103/PhysRevD.41.1456
- Hwa, R.C. and Pan, J.C. (1992) Physical Review D, 45, 1476. http://dx.doi.org/10.1103/PhysRevD.45.1476
- Jain, P.L., Sengupta, K. and Singh, G. (1990) Physics Letters B, 24, 273. Derado, T., et al. (1992) Physics Letters B, 283, 151. Albajar, C., et al. (1992) Zeitschrift für Physik C, 56, 37.
- Ghosh, D., et al. (1991) Physics Letters B, 272, 5. Ghosh, D., et al. (1996) Zeitschrift für Physik C, 71, 243.
- Schmidt, H.R. and Schukraft, J. (1993) Journal of Physics G: Nuclear and Particle Physics, 19, 1705. http://dx.doi.org/10.1088/0954-3899/19/11/006
- Kajantie, K. and Mclerran, L. (1982) Physics Letters B, 119, 203. http://dx.doi.org/10.1016/0370-2693(82)90277-5
- Bjorken, J.D. (1983) Physical Review D, 27, 140. http://dx.doi.org/10.1103/PhysRevD.27.140
- Mandelbrot, B.B. (1982) The Fractal Geometry of Nature. Freeman, New York.
- Muller, B. (1995) Reports on Progress in Physics, 58, 611. Singh, C.P. (1993) Physics Reports, 236, 147.
- Chiu, C.B. and Hwa, R.C. (1991) Physical Review D, 43, 100. http://dx.doi.org/10.1103/PhysRevD.43.100
- Jain, P.L., Singh, G. and Mukhopadhyay, A. (1992) Physical Review C, 46, 721. http://dx.doi.org/10.1103/PhysRevC.46.721








