Received 16 August 2014; revised 14 September 2014; accepted 3 October 2014

ABSTRACT

We discuss the Brouers-Sotolongo fractal (BSf) kinetics model. This formalism interpolates between the first and second order kinetics. But more importantly, it introduces not only a fractional order n but also a fractal time parameter a which characterizes the time variation of the rate constant. This exponent appears in non-exponential relaxation and complex reaction models as dem- onstrated by the extended use of the Weibull and Hill kinetics which are the two most popular approximations of the BSf (n, a) kinetic equation as well in non-Debye relaxation formulas. We show that the use of nonlinear programs allows an easy and precise fitting of the data yielding the BSf parameters which have simple physical interpretations.

Keywords:

Fractal Kinetics, Farmacokinetics, Cancer Research, Water Treatment, Adsorption, Porous Materials, Activated Carbons

1. Introduction

These last years the Brouers-Sotolongo fractal kinetics model [1] , referred as BSf model in the following, has been invoked and used in a number of problems: in biosorption kinetics [2] , non exponential kinetics of surface chemical reactions [3] , adsorption on mesoporous carbons [4] [5] and spin dynamics in magnetic systems [6] .

On the other hand many of the works (we quote some of the most recent) dealing with pharmacokinetics [7] , cancer treatment and remission kinetics are based on Hill [8] -[13] , Weibull [14] -[16] , and Tsallis [17] [18] kinetic formulas. In aqueous sorption problems especially in the treatment of air and water in environment research, the most popular formulas are the quasi-first and -second order reaction equations.

In this paper we want to show that BSf model contains all of these formulas as approximations, each of them corresponding to a particular choice of the parameters. More elaborate methods have been introduced using the notion of fractional derivative [7] . These formal developments, more sophisticated mathematically, do not change essentially the physical picture of the kinetics in complex reactions. The purpose of the formalism discussed in this paper is to give a physical meaning to the empirical formulations used in the literature and to present a formally and physically well defined model tractable computationally and amiable to further extensions.

2. The Brouers-Sotolongo Fractal Kinetic Equation

In this section we derive the equation and its various approximations encountered in the literature. The starting point is the derivation of the n-order reaction rate equation. We will consider the two cases, a decreasing and an increasing populations. For a decreasing population, we have

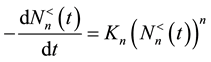(1)

whose solution is

(2)

If we use the deformed exponential [1]

(3)

and if we define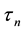

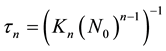(4)

we can write in a compact form

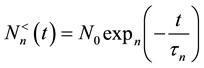(5)

with a bit of algebra one obtains a first order differential equation

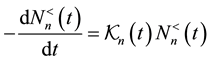(6)

with a time dependent reaction rate

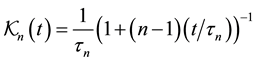(7)

For, one has a slowing down of the effective rate

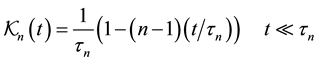(8)

and for

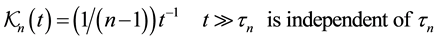(9)

These two behaviors expressing memory and aging effects appearing when.

For increasing populations, we have

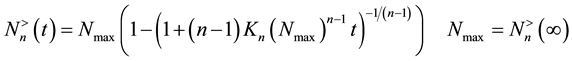(10)

(11)

(12)

(13)

(14)

For n = 1, one recovers the first order memoryless exponential decrease or increase behavior with.

These results do not exhibit the power law time dependence of the reaction rate observed in many reaction in complex chemical systems [19] and in non-Debye relaxation [20] and which led to the introduction of empirically fractal kinetics formulae [21] [22] . Here this “fractal” behavior can be introduced quite naturally if we introduce in Equations (3) and (4) instead of an n-deformed exponential, a n-deformed Weibull function as this has been done in other works on complex systems [1] [23] [24] .

(15)

with a characteristic time

(16)

The form has the form of the survival function of the Burr XII distribution [25] . The effective time-dependent rate coefficient now reads

(17)

Equation (15) is solution of a “fractal” differential equations

(18)

(19)

The effective reaction rate has two asymptotic behaviors:

(20)

(21)

For, we get the same power law variation of the rate coefficient as in the work of [19] [20] and collaborators as well as in the fractal phenomenological description of the heterogeneous reaction kinetics if we identify the Kopelman [21] fractal parameter with. As noted in [1] , the concept of effective time dependent rate breaks down as , since diverges. The general solution of the fractal differential Equation (18) does not suffer from such difficulty and is well defined in the positive time domain. In any case as for geometric fractals, for physical reasons, there appears natural cut-off which sometimes can make difficult an exact determination of the exponent.

The two asymptotic behaviors of the population evolutionary law Equation (15) are:

(22)

independent on n for while for, one has:

(23)

It is important to notice that in BSf kinetics the exponent for large t is given by the ratio involving the two exponent parameters:

(24)

For special values of the parameters n and, some usual kinetics are recovered:

1)

(25)

which is the first order kinetics.

2)

(26)

which is a “Weibull kinetics”. If, this is a “streched exponential kinetics”.

3)

(27)

(28)

This is the “Tsallis” kinetics.

4)

(29)

this is the second order kinetics.

5)

(30)

this the fractal second order or Hill kinetics.

It is important to note that as soon as, the time dependence of the kinetics depends on the initial concentration. We will call the kinetics giving rise to the population evolutionary law (30) the kinetics

(31)

(32)

For increasing population, one has

(33)

(34)

solution of

(35)

In the Weibull case, we have

(36)

The Hill equation is obtained in the case,

(37)

It is of interest to recall that the solutions (30) an (32) can be obtained from exponential kinetics by assuming a distribution of the rate constant K due to fluctuations of the exponent of the Arrhenius law: resulting from the distribution of sorption energies E. This was discussed in details in [1] . We have shown in the same paper that the equation can be also derived using the stochastic methods of the Wroslaw school [19] [20] .

3. Application of the Equation

In the application of equation in the sorption of polutents by activated carbons or other substrates in the liquid phase, one analyzes the kinetics of the dissolved molecules by gram of activated carbon absorbed at time t, (in mg/g). If the maximum adsorbed quantity is given by the equation to be used is:

(38)

When n and a are ≠1, one can no longer define a time independent rate constant and the relevant quantity characterizing the time evolution of the process is the characteristic time.

The quantity measures the sorption power and one can also define a “half-reaction time” which is the time necessary to sorb half of the equilibrium quantity and is defined by

(39)

which gives

(40)

In the case of Weibull kinetics and Hill kinetics, this reduces respectively to and .

Although the BSf model has been invoked in a number of papers, it has been used correctly in a very few. We can mention the work of Harissa et al. [26] on adsorption of pigments on algaes and the paper by S. Gaspard et al. [27] dealing with the the use of activated carbon for water treatment and where a fractal behavior has been identified clearly and a correlation made with independent measures of the geometrical fractal structure of the sorbent in the case of macroporous activated carbon.

As an illustration we have applied the equation to a set of published measurements done by the group of the Avinashilingam Deemed University [28] . These data deal with the kinetics of the adsorption of methylene blue onto the activated carbon prepared from fruits of Mimusops elengi and commercially activated carbon for comparative purpose. For each of them, the authors have considered three different initial concentrations of methylene blue. We refer to this article for the experimental conditions of concentration, temperature and pH. They have used linearization method to analyze their results. One knows the shortcomings of linear fitting and here we have used the nonlinear fitting methods of the last version of the “Matematica^c” software which allows a much better precision. As can be seen from the results, the equation leads to a better description of the process and makes easier the comparison of different sorbent-sorbate couples. The results are reported in the table for the six cases considered in [28] .

These results do not agree with the linearized calculations of [28] which concluded that the adsorption process follows a first-order kinetics. We find a clear fractal behavior with an a exponent close to 0.5 in the range of 0.35 < a < 0.65, and the order n of the reaction being 2 or larger. The regression factor is very close to 1 and in Figure 1, we show the graphical results for the case of lower R² (case 3) to demonstrate the quality of the fitting. A calculation allows to make a choice between a Weibull and a Hill approximation. Here obviously the best choice would be the Hill equation. The difference between results of case 3 and the other 5 cases shows that it is important to have results until complete saturation. And obviously the more experimental points, the

better fitting. These two simple facts are not always recognized by experimentalists and this can lead to erroneous results and the use of empirical not physical formulas.

Cite this paper

F.Brouers, (2014) The Fractal (BSf) Kinetics Equation and Its Approximations. Journal of Modern Physics,05,1594-1601. doi: 10.4236/jmp.2014.516160

References