Received 7 July 2014; revised 4 August 2014; accepted 1 September 2014

ABSTRACT

Using powerful concepts and tools borrowed from the seminal arsenal connecting physics fundamentals with esoteric set theoretical operations developed in recent years by Alexandria E-infinity theoretician M. S. El Naschie, this paper explores the deep implications of some of the dualities Dr El Naschie has identified and analyzed in his exposes, connecting them with our own Xonic Quantum Physics (XQP) which places dynamical action rather than spacetime and energy at the core of the System of the World.

Keywords:

E-Infinity, El Naschie, Space, Time, Spacetime, Topology, Cantor Sets, Energy, Xon, Xonic Quantum Physics, Planck Scale, Dirac Electron

1. Introduction

In three preceding Notes [1] -[3] we presented a System of the World in which an active principle, the Xon, generates Space and Time by “occurring” in a substrate made up of i-points bearing no geometric relations of distance or proximity with each other—in brief, which do not constitute a continuum. Our aim in the present paper is to develop this description further.

Mathematical physics is the art of using concepts and methods borrowed from evolving mathematics to formally express findings made in physics. Keeping in mind that our modern word physics derives from the Greek φύσις (phúsis) “nature”, while the word mathematics comes from the ancient Greek μάθημα (máthēma) “that which is learnt” (“what one gets to know”), we have organized this paper as follows.

We first consider an entity made up of points forming a continuum as a potentially symbolic representation of spacetime. Opposite to the Xon, we introduce an agent capable of generating voids in this continuum, the noX. We then show that in performing this deconstruction, the noX disrupts the continuum in such a way that it leaves behind a continuum containing two different kinds of points, i-points and e-points. Further on in this paper we investigate the significance of the concept of continuity, concluding that it should not be retained as a fundamental characteristic of space in general and of spacetime(s) in particular.

Next, we raise the question: Spacetime of Space and Time? We show that even the most dedicated adepts of spacetime use Time—“ordinary” time—explicitly in their considerations, thereby answering the question we just raised: Time, all and by itself, is of the essence, particularly in Quantum Physics.

We examine in this context the problems raised by the Earth’s motion(s). We show that Ampère’s famous 1820 Expérience décisive (Decisive Experiment) leads to the formulation of a startling Universal Law of Nature, first recognized as such by French genius mathematician (and theoretical physicist) Henri Poincaré in 1901: Nature appears to be engaged in a “conspiracy” which makes it impossible for Man to ascertain the Earth’s presumed motion(s) by whatever means one might imagine.

We conclude this Essay, in the spirit of the Yin and the Yang esoteric doctrine, on a philosophical note: Quantum Physics dualities—the Xon and the noX, i-Points and e-Points, Dark Energy and Ordinary Energy...— may very well be ruling the System of the World, unseen actors (dis)continuously participating in explosive series of constructive and deconstructive xonic Little Bangs.

2. Visiting Spacetime

In 1874, Saint-Petersbug born German mathematician Georg Cantor, then twenty-nine years old, published the epoch-making paper which founded Set Theory. Three years later, Cantor proved the theorem which asserts that for any positive integer n, there exists a 1-to-1 correspondence between the points on the unit line segment and all of the points in an n-dimensional space. Stunned by this discovery, Cantor exclaimed to his colleague, the mathematician Richard Dedekind, a former pupil of Gauss in Göttingen: “Je le vois, mais je ne le crois pas!” (“I see it, but I don’t believe it!”) [4] .

We shall take advantage here of Cantor’s “Je le vois” theorem to represent 4-dimensional spacetime in terms of the 1-dimensional Unit Line Segment (ULS).

Spacetime was invented in 1905 by French genius mathematician Henri Poincaré under the appellation Espace quadridimensionnel. Three years later—precisely on Monday September 21, 1908—Alexotas-born German mathematician Hermann Minkowski gave it the name “Raum und Zeit”, which soon became “Raumzeit” and was translated as “Spacetime” in English. The reader interested in the history of the subject will consult with profit Thibault Damour’s brilliantly documented essay “What is missing from Minkowski’s ‘Raum und Zeit’ lecture” which is available in arXiv [5] .

Consider the modest line segment of length 1, (0, 1), we shall call it the ULS there after. Select two points a and b on this segment, leave these two points untouched and remove (extract) all the points laying between them on the ULS. Repeat (conceptually) this deconstruction procedure on the ULS segments remaining, each time extracting the points lying between the endpoints of the segment concerned. In a remarkable paper published recently [6] , Alexandria E-infinity theoretician M. S. El Naschie has demonstrated (using a slightly different notation and vocabulary) that when conducted randomly ad infinitum in a particular fashion which he has described in detail, this iterative asymmetric process generates two complementary Cantor point sets with deeply differing significant characteristics which can be exploited to yield information of considerable physical interest.

Deeply different, these two sets share nevertheless one significant characteristic. Inasmuch as the distances between the points it contains are defined, the ULS is a metric space, a characteristic the two sets extracted from it retain. Being a line segment, the ULS has the classical dimension 1. Not so for the two sets extracted from it. Retaining the property of being metric spaces, however, they can be assigned a Hausdorff dimension, a formal generalisation of the ordinary concept of “dimension” not easily defined with words. The reader not familiar with this topological concept will find useful information concerning it in [6] .

This having been said, a subtle yet probing question arises right off the bat: in the preceding expose, how should the verbs remove and/or extract be understood? We examine this question before proceeding further on.

3. Generating Voids

In the standard language of Topology as used in the context of Cantor algebra, the verbs “remove” and/or “extract” (or delete) simply signify that the points concerned are “mathematically” removed (deleted) from the segment concerned. But what if the mathematical description does in fact relate to a deconstruction process physically taking place within the System of the World?

In the spirit of the preceding remark, and for the purpose of the present paper, we shall assign to the mathematical verbs “remove” or “extract” a more appropriate physical significance: we shall say that the points concerned are not removed from the interval segment on which they lie; we shall say instead that they remain on the segment to which they belong but have been spatially disconnected from each other in such a way that they no longer participate in the segment topological structure. One might say that their spatial interrelations have been “sublimated”.

This interpretation fares well with, and gives support to, El Naschie’s contention that the voids generated in the ULS (the TUI—Topological Unit Interval—for him) as a result of the removal iterative process described above represent Emptiness, not Nothingness.

Now if this sublimation process is not to be viewed simply as a mathematical device but corresponds in fact to a physical phenomenon, then it must result from the intervention in the ULS of a “sublimating” or “deconstructing” agent which we shall “personify” in what follows by calling it the noX for reasons which will become apparent further on in this paper.

This being, let us review the characteristics of the two complementary Cantor sets generated by this noX Iterative Deconstruction Process (nIDP), which entails, indeed, deconstructing step by step the unit line segment.

4. Giving Dimension to the Voids

As demonstrated by Dr. El Naschie, the complementary Cantor sets resulting from the ULS iterative deconstruction are:

● a Cantor point set S₀ [our designation] collecting the points left behind on the ULS during the iterative deconstruction process (these points are notably, but not exclusively, gap endpoints, see our Heading 14) having a Hausdorff dimension given by [7]

. (1a)

where ϕ designates the celebrated Golden Ratio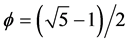. El Naschie calls this set the Zero set.

This result is remarkable in itself, in particular because if the deconstruction had been performed using the classical triadic Cantor set method for example, instead of El Naschie’s particular random technique, it would have produced a Hausdorff dimension having the more banal value ln2/ln3. Dotted with outstanding properties, the singularly irrational Golden Ratio ϕ is indeed a true marvel of Nature [8] . To encounter it in the present context constitutes a most inspiring occurrence.

The result is also remarkable for another reason. The points left over on the ULS after the noX deconstruction has occurred are points which have retained the positions they originally occupied on the ULS, thereby remaining in relations of distance, if not of proximity, with each other. They are not i-points. Let us call them e-points.

● a Cantor set S_E [our designation] collecting the gaps generated in the ULS by the iterative deconstruction, i.e. a set collecting the points still in the gaps but spatially disconnected during the noX sublimation process according to our scheme. It possesses a Hausdorff dimension given by

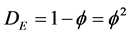(1b)

El Naschie calls this set the Empty set since it is made up of voids.

This set is of special interest to us in the present paper, notably because, as pointed out by El Naschie himself, the gaps—the voids—it contains are regions of No space and No time.

No space and No time… As per our definition, the points this set contains are points which bear no relations of distance or proximity with one another. They are not e-points, they are i-points!

Let us investigate how the Xon generates space (lengths) by “occurring” in their midst.

5. Xonic Quantum Physics

We shall reason within the framework of the theoretical scheme we have presented in our three preceding papers [1] -[3] , referred to collectively in the present paper as constituting Xonic Quantum Physics (XQP).

We have allowed our deconstructing agent, the noX, to intervene in the ULS, disrupting its topological structure. We now allow the Xon—counterpart to the noX—to intervene—to occur—in the Empty set gaps, thereby generating topological connections between the i-points present in the gaps according to the Leibniz-De Broglie fundamental relation

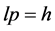(2)

in which l designates a (space-like) length, p an associated (linear) momentum, and h the dynamical action element carried by the Xon—Planck’s “constant”. This equation places dynamical action rather than energy (or spacetime) at the heart of Quantum Physics.

There is no compelling reason, of course—quite to the contrary—to assume that the length referred to in Equation (2) has some kind of Euclidean structure. It is more likely to constitute, at best, a fractal. All these considerations have been exposed and justified in some detail in our initial presentation of XQP [1] .

The Xon generates space elements (lengths). We now examine how it also generates time elements (durations).

6. Generating Durations

In calculations L. MarekCnjac carried out recently with Dr El Naschie [9] , these two authors make use of what they call “Einstein’s iconic formula for the maximal total energy of a classical particle” corresponding to the famous mass/energy relation E = mc².

The mass/energy relation was originally discovered (before Einstein) as m = E/c². When used in this form, the “iconic formula” provides a simple way to convert Equation (2) into an equation involving time, and more precisely, involving a time lapse or duration.

This arises as follows.

In Equation (2), the factor p designates the linear momentum imparted on substrate i-points by the acting Xon. I-points have Zero dimension, hence we can safely assume that they also have Zero mass (like the incongruous photon). The momentum they acquire is therefore given quite simply by

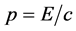(3)

where c designates the Xon message velocity which travels the (linear) distance l in a time lapse (time duration) d. Equation (3) then reads

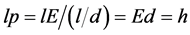(4)

as a result of which we now have duration as well as space lengths in the reconstructed ULS segment.

This remark gives us a clue to the role our e-points might play in nature. Taken together, they form a set which is discontinuous but orderly: the points it contains follow each other in a certain order.

They are the points the Xon uses to generate… time durations.

Thus defined, time does not pass, it does not flow; it ticks and it lasts.

In |6], El Naschie went on to connect the Cantor set S₀ to the “ordinary energy” of a “quantum particle” and the Cantor set S_E to “dark energy” forming a “Halo” in the cosmos.

We shall examine this proposal. But before doing so, let us summarize the first outstanding new results our analysis has yielded.

We started with the premise of a substrate presumably present in nature made up of i-points bearing no geometric relations of distance or proximity with each other, and of e-points which retain a relation of order with respect to one another. If our analysis is correct, it then follows that spacetime itself (assuming for the time being that it exists as a physical entity partaking in the fabric of the universe) must contain the two kinds of points, i-points and e-points, a characteristic not hitherto recognized as an attribute of spacetime.

Hermann Minkowski died tragically at age forty-four less than four months after he had delivered his famous “Raum und Zeit” lecture in Cologne. He left a legacy concerning spacetime less than satisfactory on several counts [5] . One of them bears on the bold prophecy he professed as a kind of conclusion to his lecture: “Henceforth, space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality”.

Let us investigate why this prediction has not materialized.

7. When Time is of the Essence

Paleontologists will tell you—should you happen to be asking them...—that Dinosaurs first appeared during the Triassic period 231.4 million years ago and were “the dominant terrestrial vertebrates for 135 million years [our emphasis] [10] ”. Thus time—”ordinary” time, measured in years and capable of passing—enters as a fundamental structural ingredient in the way paleontologists see (conceive) the functioning of the System of the World: for them, time has been ticking as “ordinary time” during at least these millions of years—way before anyone was there with a clock to measure its passing.

General Relativity physicists will tell you by contrast—even if you should not happen to be asking them!— that time does not exist as such, only as a (hidden) ingredient of curved spacetime. Other physicists will tell you however—upon hearing what the General Relativity people have been telling you...—that their (generally accepted) Big Bang theory provides a (generally accepted) cosmological model for the early development of the universe. The Big Bang occurred approximately 13.798 ± 0.037 billion years ago, they will explain. And they will add: “At this time [again, our emphasis] the universe was in an extremely hot and dense state and began expanding rapidly.” Then they will conclude: “After the initial expansion, the universe cooled sufficiently to allow energy [once more, our emphasis] to be converted into various subatomic particles, including protons, neutrons and electrons [11] .” The terms we have emphasized in the preceding paragraphs refer to processes involving yesterday, today and presumably tomorrow—in brief the passing of time.

Relativistic spacetime was invented for one specific reason—to resolve one specific difficulty physicists encountered in their researches that we shall now examine.

8. Time Is Ticking

Is It Not?

Suppose nothing moves, suppose nothing changes. Then time, as we know it here on Earth, would be standing still. We would not be able to say that it is passing—that it is ticking.

The passing of time is motion in disguise (clocks).

The Earth rotates around its NS axis at the rate of one rotation in approximately twenty-four hours. It also moves on its orbit around the Sun at the rate of about one full orbit in some three hundred and sixty-five days.

The Sun is a star belonging in the Milky Way, a spiral galaxy composed of two major spiral arms connected by a “bar” which contains an estimated one hundred to four hundred billion other stars. The Solar System, hence the Earth with it, is located on the inner edge of one of the spiral-shaped arms, the so-called Orion Arm.

The Milky Way is one of the many billions of galaxies which together form the Universe. As a whole, it moves at a velocity in the order of six hundred km/sec as measured with respect to (imaginary) extragalactic frames of reference.

Distant galaxies are seen to recede from the Milky Way—and us from them—at velocities approaching the speed of light. In fine, how fast—and in what direction—is the Earth moving?

The Earth is moving, that’s for sure—Eppur si muove (Galileo).

Very well, then, let us attempt to prove or demonstrate that the Earth IS moving.

9. The Decisive Experiment

Henri Poincaré found in 1901 an astonishingly simple and easy way to prove whether or not the Earth is moving. He formulated the following proposal:

Place two static electric charges of equal sign—say negative—a short distance from each other somewhere— anywhere—on the surface of the Earth. If the Earth is moving, it carries with it the two charges in its motion. Then by well established laws of electrodynamics the following apply:

1) The two moving charges are equivalent to—produce the same effects as—continuous (DC) electric currents (Rowland, Berlin, 1870s).

2) Running parallel to each other and flowing in the same direction, the two continuous currents must attract each other—they would repel each other if they ran in opposite directions (A. M. Ampère’s Expérience Décisive—The Decisive Experiment—Paris, 25 September 1820 [12] ).

3) Fact: the two charges do not attract each other; at best, they repel each other.

10. Conclusion

Either the Earth is not moving—it is, as the Ancients believed, immobile at the centre of the Universe.

Or....

11. A Startling Universal Law Rules the System of the World

Wise, prudent and... daring, Henri Poincaré recalled how, on February 26, 1616, his great predecessor Galileo Galilei had been called to cardinal Roberto Bellarmine’s residence in Rome to be ordered (on formal instructions from Pope Paul V) “to abandon completely [...] the opinion that the Sun stands still at the center of the world and the earth moves, and henceforth not to hold, teach, or defend [this doctrine] in any way whatever, either orally or in writing” [13] . Now, nearly three centuries later, how was he, Poincaré, to tell his contemporaries that maybe, after all...

Incidentally, a great expert in Analysis Situs—but in what field of mathematics and/or physics and/or philosophy, was he not an expert...—Poincaré found a way. He let it be known that Nature appears to be engaged in a “conspiracy” to make it impossible for Man to ascertain the Earth’s presumed motion(s) bywhatever means one might imagine. In brief, for all practical purposes, the System of the World functions as if the Earth does not move, thereby apparently giving comfort to cardinal Bellarmine’s 1616 admonition to Galileo.

12. Games the Electromagnetic Field Plays

Whether the Earth moves or does not move, we certainly can move or observe motion, notably linear uniform motion—motion at constant speed on a straight line—on the Earth. But there too, something strange occurs. Galileo—him again—noticed it.

Place on a boat a cage containing flying animals such as butterflies or birds and a jar containing fishes swimming in water. Observe their comportment. The flying animals and the fishes behave exactly the same whether the boat is still at bay in Venice or moving on a straight course at constant speed on a calm sea. In brief, uniform (linear) motion produces no detectable effects—é come nullo.

But behold!

In 1864, Scottish virtuoso mathematician James Clerk Maxwell, then professor of Natural Philosophy at King’s College in London, informed the scientific community that an entity he called the Electromagnetic field perverts space uniformly. He supplied a set of eight (partial differential) equations (later extended to twenty then reduced to four in algebraic vector notation) describing the characteristics and presumed behaviour of this field [14] . To construct his theory, Maxwell referred to a number of concepts and symbols, some borrowed from his contemporaries or predecessors—Oersted, Ampère, Gauss...—, others of his own invention, many of which have since then become obsolete: the magnetic Intensity H; the current Density J; the electric Displacement D; the quantity of free Electricity ρ; the angular Impulse A; the electromagnetic Force E; the electromagnetic Potential φ; the specific Resistance σ... by means of which he expressed eight mathematical laws supposed to govern the field: the Law of total currents; the Equation of magnetic force; Ampère’s circuital Law; the electromotive Force created by convection, induction and by static electricity (later renamed the Lorentz force); the electric elasticity Equation; Ohm’s Law; Gauss’s Law; and the Equation of continuity.

The impact of this work was considerable... particularly when it was found that the Maxwell Equations system does not conform to Galileo’s precept that uniform motion é come nullo.

Indeed, consider the following situation.

Repeat Poincaré’s conceptual two charges experiment, but instead of two charges use two infinite parallel sheets of equal uniform static areal charge density. By Gauss’ Law, which Maxwell’s Equations incorporate, the two plates repel each other. Now imagine an observer travelling at constant linear speed between the plates. By Rowland’s Rule (see Section 5 above), this observer will see two currents flowing parallel to each other and in the same direction on the surface of the plates. Then, by Ampère’s Decisive Experiment, flowing in the same direction the two currents must attract each other, thereby decreasing the net (repulsive) force between the plates.

This does not happen.

Deeming the situation intolerable, physicists did their best to remedy it.

Did they attempt to modify Maxwell’s Electromagnetic Theory?

They eventually replaced it by Feynman’s Quantum Electrodynamics, the famous QED. But they first decided to pally the difficulty by inventing... the theory of Relativity.

The rest is legend—except for this.

13. Spacetime Is an Optical Illusion

In 1905 and thereafter, mathematicians and physicists combined their efforts to invent relativistic spacetime—a four-dimensional continuum in the Poincaré-Minkowski original invention; still a continuum but made to be flexible in the Grossmann-Hilbert General Relativity system adopted by Einstein in 1915; augmented to five dimensions in the Kaluza-Klein (K-K) model—in the framework of which Maxwell’s Equations could continue to regulate the System of the World unchanged and without violating Poincaré’s Universal Law which stipulates that Nature conspires to make it impossible for Man to measure the motion(s) of the Earth and its (presumed) quasi uniform linear orbital motion in particular.

Maxwell’s Electromagnetic Theory has now given way to Quantum Electrodynamics, but the concepts of relativity and spacetime which the Maxwell’s original system brought into being are still with us. This leaves unresolved the fundamental question: is the very concept of spacetime still relevant in the context of contemporary modern physics and notably in the contexts of Quantum Physics and E-infinity theory? Or does it constitute an “object” worthy of figuring in the Museum of Obsolete Concepts (the MOC)…?

We now address this fundamental question: why would the spacetime continuum thus continuously de-and-reconstructed (as per our scheme) appear to us to form a continuum?

14. Spacetime Does Not Exist… and Is Discontinuous!

One characteristic shared by most, if not all, variantes of spacetime, is their ambition to describe a physical continuum supposedly partaking in the fabric of nature.

In his article On the Foundations of Geometry published in 1898 (and expanded further in 1903), Henri Poincaré investigates the reason we perceive space as being a (three dimensional) continuum [15] . He ascribes the phenomenon not to a requirement of space itself, but to the way we combine and interpret “impressions” we receive from the external world. Briefly outlined, and somewhat translated, his argument runs as follows.

Divers impression systems, originated in the external world, are transmitted to our brain, which then compares them among themselves. Often, two of these systems cannot be distinguished from one another, or they can be distinguished from one another, yet not from a third system intermediate to both. When this happens, these systems, taken together, generate a “physical continuum”, each impression system being an element of the continuum.

Poincaré gave a concrete example of the scheme thus established.

Assume we can distinguish an object A, measuring 10 mm, from an object C, measuring 12 mm, but cannot distinguish either one from an object B measuring 11 mm. For us, A, B, C … then constitute a continuum, even though this continuum does not necessarily possess objective reality. Indeed, its structure leads to intolerable logical difficulties. In the example given above it yields the relations A = B, B = C, A < C. To alleviate this logical inconsistency, Poincaré introduces the notion of a mathematical continuum in which the constitutive elements do not overlap each other, as they do in the physical continuum, leading to the logically acceptable relations A < B, B < C, A < C, in the example considered.

This has been said. Let us return to our main purpose.

15. Structuring a Five Dimensional Spacetime

In his all-important May 2013 paper [13] , El Naschie uses the two Cantor sets which arise from the deconstruction process just described to construct two five dimensional Kaluza-Klein spacetimes.

The choice of five dimensions instead of four, as in the more famous General Relativity spacetime, is not a surreptitious choice. It derives from the fact that the construction with five dimensions rather than four leads to particularly attractive results for the physical interpretation. This again is related to the outstanding mathematical properties of the Golden Ratio, as we shall see presently.

For the Zero set S₀, El Naschie constructs a quasi Hausdorff five dimensional hyper volume having the topological density

(5a)

and for the Empty set S_E, a quasi Hausdorff five dimensional hyper volume having the topological density

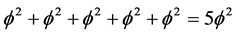(5b)

In both instances the five dimensions are homogenous—one of them is not time-like in particular unlike the other four which are obviously space-like. In brief Time—and more precisely time duration—is conspicuously absent from this construction.

Time is generally said to be passing. Energy is generally thought to be stored and eventually spent.

El Naschie recognizes the K-K five dimensional spacetimes constructed according to the procedure described above to contain energy in two distinct forms: “ordinary energy”, said to be present in the volume ϕ⁵ which originated in the Cantor set S₀, and “dark energy” forming a Halo in the volume 5ϕ²which originated in the Cantor set S_E.

How are these energies generated?

According to the XQP (re)construction scheme of the two Cantor sets under consideration, set S_E results from the occurrence of an active principle, the Xon, in the substrate formed by ULS points which have been disconnected in the noX deconstruction process of the ULS—i-points in our terminology. We are thus led to consider that dark energy is the result of the occurrence of the Xon in an i-points substrate—precisely as we originally imagined in our paper [1] .

The idea that “dark energy” might have an origin different from that of “ordinary energy” is compatible with the fact that, as per our analysis, ordinary energy originates in set S₀ which contains the points left over from the original structure—they have retained their original positions on the ULS and are therefore in relations of distance with each other. They are not i-points. We did call them e-points. Let us briefly examine what they might be.

The deconstruction scheme which leaves behind the Cantor set S₀ with the desirable Hausdorff dimension 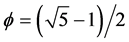is not quite the same as the deconstruction scheme which generates the classic triadic Cantor set C₃which has the more ordinary Hausdorff dimension ln2/ln3. We shall nevertheless use the classic triadic model here to illustrate as simply as possible what might be involved.

The “triadic” Cantor set C₃ arises when ULS points located at positions 1/3 and 2/3 on the ULS segment considered are iteratively left untouched (with some other untouched points, e.g. the point 1/4) as endpoints of each segment removed to constitute cumulatively the set C₃ in the end. In this particular case, the positions of the points thus left behind on the ULS are specified by the straightforward formula k/n² with k, n integers and k ≤ n, as is easily verified, yielding a spectrum reminiscent of the Schrödinger prediction for the energy levels of the hydrogen atom, 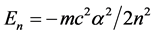, where n is an integer, m the electron mass, c the speed of light and α the illustrious Sommerfeld Fine structure constant.

[We should note, passim, that the Sommerfeld formula for his so-called fine structure constant α yields interesting XQP information when (re)written as e²/2παc = h, which is our Equation Ed = h for the special case when the Leibniz intensio factor E has the particular value 2παe²/l representing the repulsion two “charges” e exert on each other when held at a distance l/2πα apart, where l measures the length light would have covered over the duration d. It might be worthwhile to undertake further exploration of this result.]

Is the Cantor set S₀ physically realized in Nature?

Many other sets having interesting Hausdorff dimensions have been identified. The interested reader will find a comprehensive list of such sets in [16] . As of this writing, we have made no further attempt to probe this aspect of the problem.

16. Does the Planck Scale Pose a Problem?

One last remark before ending this presentation.

E-infinity theoreticians—and General Relativity physicists in general—are deeply preoccupied by the implications the so-called “Planck scale” might bear on their theory. At this scale, they say that the concepts of size and distance “breakdown” as quantum indeterminacy become virtually absolute [17] .

In Xonic Quantum Physics, the relations lp = h and Ed = h which define space lengths and time durations respectively are valid at all scales and do not imply an assumed “quantum indeterminacy”—quite the contrary: they are the very foundations of the theory. We illustrate this fact by considering the following contemporary example.

Tokyo Metropolitan University mathematical physicist Shigeru Sasabe recently published in this Journal a paper entitled “Spin-Magnetic moment of Dirac Electron and Role of Zitterbewegung” [18] .

The very existence of a magnetic moment associated with the electron is one of the vexing questions a Quantum Physics theoretician has to face—how, why does the magnetic moment arise. We showed that there is a xon signature in the electron spin [2] . S. Sasabe proposes his own answer to this vexing question: “[The Dirac] electron spin-magnetic moment, he suggests, may be caused not by usual electric current but by some new current [generated] when the electron undergoes transition between two states of positive and negative energies.”

The novel and imaginative solution Shigeru Sasabe thus presents and defends in his paper—a “transition current” capable of generating a magnetic moment as an ordinary circular electric current would—constitutes an attractive proposal in itself. It also opens up another perspective that we shall now examine.

Under the heading “Concluding remarks”, the author asserts: “In quantum theory, the conservation law of energy may break by ΔE in time Δt, where ΔEΔt ≅ ћ.”

In this equation, as is usual nowadays, the author presents Planck’s constant h in its “reduced form”, also called Dirac’s constant, ћ = h/2π.

This apparently innocent choice raises in fact a deep question concerning the proper use of the symbol h in Quantum Physics.

In 1900, Max Planck made the fortuitous discovery that dynamical action—Actio to its inventor, Leibniz— occurs in Nature in the form of tiny elements—elementary quanta to Planck—all carrying the same amount— the same “quantity” or quantum—of said dynamical action. Planck proposed to represent this elementary quantity—this elementary quantum—by the symbol h. It follows that the “reduced form” ћ = h/2π, which represents less than a sixth of h, is at best a physically meaningless symbol: a “quantum” of action can never be found in Nature having the value ћ or integral multiples of it.

The factor 2π is not significant in the context of the present considerations. We shall therefore rewrite Shigeru Sasabe’s equation more simply as ΔEΔt ≅ h. With ΔE = E and Δt = d, in a slightly different notation, this is our equation Ed = h. Sasabe’s “energy current” is thus shown to be governed by one of the two XQP fundamental rules, a most rewarding result.

17. (Optimistic) Concluding Remarks

M. S. El Naschie’s E-infinity theory proposes intriguing connections between set theoretical concepts and quantum mechanical wave-particle dualities. Pursuing this endeavor in the present paper in the framework of our own Xonic Quantum Physics theory, we have encountered new dualities which remind us of the ancient philosophy of the Yin and the Yang which invokes complementary rather than opposing forces interacting to form a dynamic system in which the whole is greater than the assembled parts. We summarize our most significant findings in this regard:

● The System of the World is run by two complementary active principles

the ↓☻◄ noX and the Xon ►☺↑

● The noX deconstructs clusters formatted by the Xon, leaving behind a discontinuous substrate containing two kinds of points

i-points ◦ and ◘ e-points.

● The Xon generates Space and Time (rather than Spacetime) in the form of

space lengths├ and ┤time durations.

● Energy may exist in the cosmos in two complementary forms

dark energy ◙ made from i-points and ordinary energy ☼ made from e-points.

● In fine, we are in the presence of two complementary theoretical approaches to Quantum Physics

E-infinity ♠ and ♦ XQP.

In conclusion, let us briefly return to the question we raised earlier in this paper: is the concept of spacetime still relevant in the context of contemporary modern physics and notably in the contexts of Xonic Quantum Physics and E-infinity theory?

Our analysis leads to this fascinating answer:

The continuous (compact) Unit Line Segment we used to represent spacetime in this paper hides in fact a subjacent reality consisting of two discontinuous complementary Cantor sets containing two different kinds of points—i-points and e-points by our terminology. The same might be true of continuous relativistic spacetime(s). They might, at best, represent superficial representations of a hidden discontinuous reality in the secret of which the noX and the Xon perform (dis)continuously what we have called in our paper [3] xonic Little Bangs which result in (dis)continuously constructing and deconstructing the structural elements of the System of the World—space lengths and time durations.

General Relativity physicists do not regard their 4-dimensional pseudo-Riemannian manifold spacetime as constituting an approximation, however. To them it describes THE fundamental structural ingredient of the universe (together with energy!). The problem is, Quantum Physics’ main ambition is to probe the System of the World’s (hidden) inner workings. If it is to preserve whole heartedly its integrity, Quantum Physics must then be unwilling to accommodate in its midst a concept which hides by smoothing them out discontinuities inherent to the System. For this reason, if for none other, we submit that the spacetime of General Relativity be placed as a venerable reliquary in the Quantum Physics Museum of Obsolete Concepts (the QPMOC), alongside with such other honorable imaginative inventions of yesteryears as Faraday’s Physical Lines of Forces, Ampère’s Conflit Electrique, Maxwell’s Displacement Current, Lorentz’s Luminiferous Aether, Planck’s Energy Elements, together with… why not, an effigy of Nessesiteras Rhombopteryx, the Loch Ness Monster (Nessie) which entertained us for a while with the inspiring impression of being an engaging Reality.

Acknowledgements

We wish to express our appreciation to Ms. Kelly Sang, JMP Editorial Board Assistant for her valuable help and advice in properly formatting this paper for publication.

References