Journal of Modern Physics
Vol.5 No.8(2014), Article
ID:46360,18
pages
DOI:10.4236/jmp.2014.58071
The Proof That There Are No Invariabilities of Lorentz Transformations in the Interaction Theories of Micro-Particle Physics
Xiaochun Mei
Institute of Innovative Physics, Fuzhou, China
Email: ycwlyjs@yeah.net
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 March 2014; revised 13 April 2014; accepted 12 May 2014
Abstract
It is proved in this paper that there are at least five situations in the interaction theories of microparticle physics that the Lorentz transformations have no invariabilities. 1) In the formula to calculate transition probabilities in particle physics, the so-called invariability factor of phase space d3p/E is not invariable actually under the Lorentz transformations. Only in one-dimensional motion with uy = uz = 0, it is invariable. 2) The propagation function of spinor field in quantum theory of field has no invariability of Lorentz Transformation actually. What appears in the transformation is the sum of Lorentz factors aμνaλμ ≠ δνλ when ν, λ = 1, 4, rather than aμνaλμ = δνλ. But in the current calculation, we take aμνaλμ = δνλ. The confusion of subscript’s position leads to wrong result. 3) Though the motion equations of quantum fields and the interaction Hamiltonian are unchanged under the Lorentz transformation, the motion equation of perturbation which is used to calculate the transition probability in the interaction representation has no invariability. 4) The interactions between bound state’s particles have no Lorentz invariability. In fact, the principle of relativity has no approximation if it holds. 5) The calculation methods of high order perturbations normalization processes in quantum theory of fields violate the invariability of Lorentz transformation. The conclusions above are effective for strong, weak and electromagnetic interactions and so on. Therefore, the principle of relativity does not hold in the micro-particle’s interactions. On the other hand, the invariability principle of light’s speed is still effective. So the formulas of special relativity still hold, but we should consider them with absolute significances.
Keywords:Principle of Relativity, Lorentz Invariability Violation, Quantum Theory of Filed, Quantum Mechanics, Phase Space Factor, Propagation Function, Normalization, CMBR, Cosmology

1. Introduction
The Einstein’s special relativity is based on two foundational principles. One is the principle of relativity and another is the invariability of light’s speed. According to the principle of relativity, motion is a relative concept. We cannot determine whether a reference frame is moving in a uniform speed or at rest by physical experiments. Speaking more strictly, the forms of physical laws are unrelated to the choices of reference frames. To reach this aim, physical quantities should be covariant under Lorentz transformations.
Because most macro-physics involve low speed’s processes, special relativity is mainly used in micro-physics processes. Micro-physics includes relativity quantum theory of field and non-relativity quantum mechanics. Because the motion equations and interactions Hamiltonians in quantum theory of field are considered invariable under Lorentz transformation, physicists believes that interaction processes of micro-particles satisfy the principle of relativity.
However, astronomic observations founded that the cosmic microwave background radiation (CMBR) was anisotropic in space distribution. If we take the reference frame in which CMBR is isotropic as an absolutely static reference frame, observations indicate that our solar system is moving in a speed about 390 Km/s along a certain direction in the coordinate system of celestial sphere. This velocity can be considered as the absolute velocity of solar system. In fact, Big Bang cosmology needs an absolutely static reference frame. We can think that all initial velocities of materials in the universe were caused by the accelerating processes in Big Bang. So physics is in a dilemma situation at present. Cosmology and relativity are inconsistent. This is a serious problem.
In this paper, we prove that the principle of relativity is only a subjective and specious judgment under macroscopic and low speed’s conditions, just as Galileo’s intuitional experiments in a closed ship. Under microscopic and high speed’s conditions, the principle of relativity does not hold. In fact, the principle of relativity has never been accurately verified by experiments. Physicists have never carried out experiments in a reference frame with high enough speed to verify the correctness of relativity principle!
In the processes of micro-particle’s decays and collisions, the transition probabilities are considered having nothing to do reference frames. Quantum theory of field is constructed in this principle and the interaction theories of micro-particles are considered satisfying the principle of relativity. However, in this paper, we carefully examines the motion equations and the interaction Hamiltonians of micro-particles in quantum theory of field and finds that at least in five situations the interaction theories of micro-particles have no invariability under Lorentz transformation.
1) The so-called invariability factor of phase space 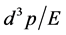 in the formulas of transition probability has no invariability of Lorentz transformation actually. Only in the one-dimensional motion process with
in the formulas of transition probability has no invariability of Lorentz transformation actually. Only in the one-dimensional motion process with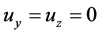 , it is invariable. The result indicates that all transition processes of micro-interactions have no invariabilities under Lorentz transformation. The commutation relations of field operators have no invariability due to this result.
, it is invariable. The result indicates that all transition processes of micro-interactions have no invariabilities under Lorentz transformation. The commutation relations of field operators have no invariability due to this result.
2) The propagation function of spinor field has no the invariability of Lorentz Transformation actually. What appears in the transformation is the sum of Lorentz factors 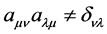 when
when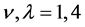 , rather than
, rather than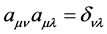 . But in the current calculation, we take
. But in the current calculation, we take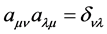 . The confusion of subscript’s position leads to serious mistake.
. The confusion of subscript’s position leads to serious mistake.
3) Though the motion equations of gauge fields and spinor fields and the interaction Hamiltonians are unchanged under Lorentz transformation, the motion equation of perturbation theory used to practically calculate the transition probabilities in interaction representation has no Lorentz invariability. In fact, even the most foundational normalization formulas of probability wave in quantum theory of field and quantum mechanics have no invariability of Lorentz transformation too. Unfortunately, these problems are neglected at present.
4) The interactions between bound state’s particles violate the invariability of Lorentz transformation. In fact, so-called relativity quantum theory of field only describes interaction processes in which particles are free at their initial and final states. The Hamiltonians of interactions are constructed by free particle’s wave functions. What are measured in experiments are free particles at final states. Because the wave functions and the products  of four-dimensional momentum of free particles are invariable quantities of Lorentz transformations, the probability amplitudes of transitions are invariable.
of four-dimensional momentum of free particles are invariable quantities of Lorentz transformations, the probability amplitudes of transitions are invariable.
However, in physics, more are the interactions between bound particles in which the wave functions, energies and momentums have no symmetries of free particles. We have 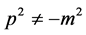 so that the product
so that the product 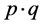 is not the invariable quantity of Lorentz transformation again. The interaction Hamiltonians cannot be constructed by free particle’s wave functions and physical quantities. The method of quantum theory of field may be ineffective. In this paper, we prove that the interactions between bound state’s particles have no Lorentz invariability by several examples just as the scatting process of electrons in external field, the fine structure of hydrogen atomic energy levels and the emission and absorption of photons in atoms.
is not the invariable quantity of Lorentz transformation again. The interaction Hamiltonians cannot be constructed by free particle’s wave functions and physical quantities. The method of quantum theory of field may be ineffective. In this paper, we prove that the interactions between bound state’s particles have no Lorentz invariability by several examples just as the scatting process of electrons in external field, the fine structure of hydrogen atomic energy levels and the emission and absorption of photons in atoms.
According to current understanding, relativity quantum theory of field describes unstable particles with high speed, and non-relativity approximate quantum mechanics describes stable particles with low speeds. This classification is unsuitable for the principle of relativity principle. The principle of relativity has no approximation. If the principle of relativity is correct, it should also be effective for the micro-particles with low speeds. In fact, classical Newtonian theory also satisfies the principle of relativity. The motion equations of Newtonian mechanics are unchanged under the Galileo’s transformation. However, the motion equations and Hamiltonians of nonrelativity quantum mechanics cannot keep unchanged no matter under the Galileo’s transformation or the Lorentz’s transformation. This fact indicates that micro-particle physics has no relativity in essence! So called nonrelativities of motion equation and interaction Hamiltonians in quantum mechanics are not caused by the approximation methods of descriptions. The truth is that relativity does not exist in micro-physics at all!
5) The normalization processes of high order perturbations in quantum theory of fields violate the invariability of Lorentz transformation. We take the Lamb shift of hydrogen atomic energy levels as concrete example at first and then prove the conclusion generally.
The conclusions above are generally effective for strong, weak and electromagnetic interactions. Therefore, the principle of relativity does not hold in the fields of micro-particle’s interactions. However, the invariability principle of light’s speed is still effective. It means that the formulas of special relativity can still hold. But they should be explained with absolute significance.
In this way, the experiments of micro-particles and the observations of macro-cosmology become consistent and the contradiction between cosmology and special relativity can be eliminated thoroughly.
2. The Lorentz Transformation of Phase Space Factor
2.1. The Invariability Quantities of Lorentz Transformation in Particle Physics
In particle physics, the basic formula to calculate the decay probability in particle physics is [1]
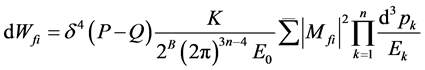 (1)
(1)
The basic formula to calculate the collision cross-sections is
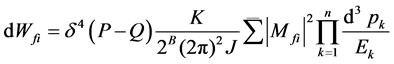 (2)
(2)
In the formulas, the probability amplitude  is the factor of dynamics and others are kinetic factors.
is the factor of dynamics and others are kinetic factors. 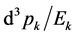 is the factor of phase space for the
is the factor of phase space for the ![]() outgoing particle at final state. All text books and documents consider this factor as the invariable quantities of Lorentz transitions. However, it is not unless in one-dimensional motion with
outgoing particle at final state. All text books and documents consider this factor as the invariable quantities of Lorentz transitions. However, it is not unless in one-dimensional motion with .
.
Before proving it, we need to define the invariable quantity of Lorentz transformation. In Einstein’s special relativity, physical quantities are transformed in the forms of covariance. Suppose that there is a physical quantity 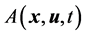 composed of space-time coordinates and particle’s velocity in the inertial reference frame
composed of space-time coordinates and particle’s velocity in the inertial reference frame . It may be a scalar, vector or tensor (subscripts are neglected). We transform it to the reference frame
. It may be a scalar, vector or tensor (subscripts are neglected). We transform it to the reference frame ![]() which moves in a uniform speed
which moves in a uniform speed 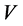 relative to
relative to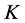 . If obtained
. If obtained  contains relative speed
contains relative speed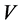 , we say that the physical quantity is not the invariable quantity of Lorentz transformation. If it does not contain
, we say that the physical quantity is not the invariable quantity of Lorentz transformation. If it does not contain 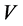 and the relation that
and the relation that 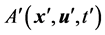 depends on
depends on ![]() is the same as that
is the same as that 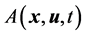 depends on
depends on![]() , we say that it is the invariable quantity of Lorentz transformation.
, we say that it is the invariable quantity of Lorentz transformation.
We take several examples commonly appearing in particle physics. Suppose that ![]() moves along the positive direction of
moves along the positive direction of ![]() axis relative to
axis relative to , the Lorentz coordinate transformations are (set
, the Lorentz coordinate transformations are (set ).
).
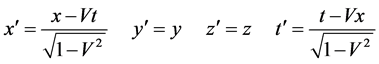 (3)
(3)
The inversed transformation of (3) is
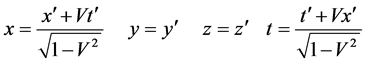 (4)
(4)
The Lorentz transformations of velocities are
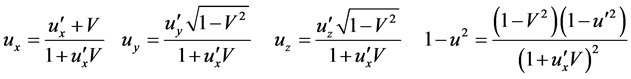 (5)
(5)
So space-time coordinates  and velocities are not the invariable quantities of Lorentz transformation, but
and velocities are not the invariable quantities of Lorentz transformation, but 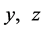 are unchanged. In reference frame
are unchanged. In reference frame , momentum and energy of a particle with mass m are
, momentum and energy of a particle with mass m are
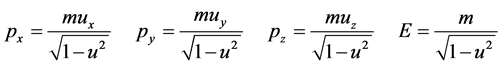 (6)
(6)
Substituting (5) in (6), we obtain the Lorentz transformations of momentum and energy
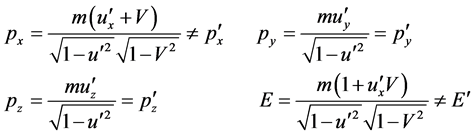 (7)
(7)
So ![]() and
and  are the invariable quantities of Lorentz transformations, but
are the invariable quantities of Lorentz transformations, but 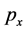 and
and 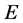 are not. Writing them in the four-dimensional forms with
are not. Writing them in the four-dimensional forms with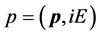 , we have
, we have
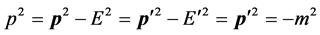 (8)
(8)
So ![]() is the invariable quantities of Lorentz transformation, thought it is equal to a constant. The factor
is the invariable quantities of Lorentz transformation, thought it is equal to a constant. The factor ![]() in (2) is also the Lorentz invariable quantity
in (2) is also the Lorentz invariable quantity
 (9)
(9)
We can prove it easily. According to (6), we have
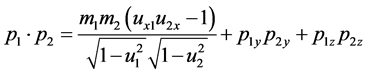 (10)
(10)
According to (7), we get
 (11)
(11)
In particle physics, similar invariable quantities are
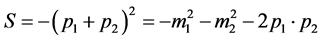 (12)
(12)
 (13)
(13)
Meanwhile, we have
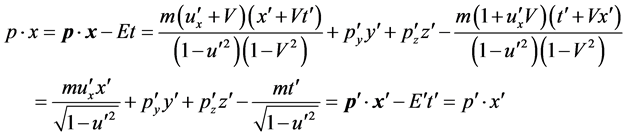 (14)
(14)
So the wave function of free particle is also the invariable quantities of Lorentz transformation with
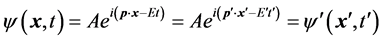 (15)
(15)
The definition of ![]() function in particle physics is
function in particle physics is
 (16)
(16)
Transforming it to ![]() reference frame, because
reference frame, because ![]() and
and  are unchanged, we only need to calculate the relation between
are unchanged, we only need to calculate the relation between 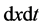 and
and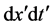 . By using the Jacobi’s matrix of integral transformation, we have
. By using the Jacobi’s matrix of integral transformation, we have
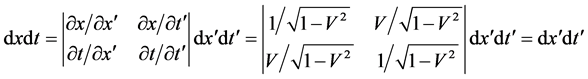 (17)
(17)
So  and (16) are also the invariable quantity of Lorentz transformation with
and (16) are also the invariable quantity of Lorentz transformation with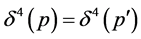 .
.
2.2. The Lorentz Transformation of Phase Space Factor
If phase space factor is the invariable quantity of Lorentz transformation, it should satisfy
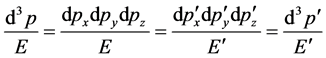 (18)
(18)
We will prove that (18) only holds in the situation of one-dimensional motion with . In general situation when
. In general situation when 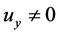 and
and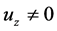 , (18) is untenable. Because
, (18) is untenable. Because ![]() and
and 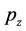 are invariable with
are invariable with  and
and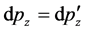 , we only need to discuss
, we only need to discuss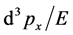 . In
. In  reference frame, we have
reference frame, we have
 (19)
(19)
here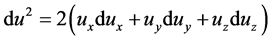 . In the situation of one-dimensional motion with
. In the situation of one-dimensional motion with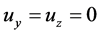 , we set
, we set 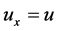 and have
and have
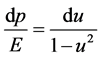 (20)
(20)
On the other hand, in general situations with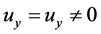 , according to (5), we have
, according to (5), we have
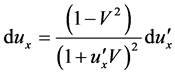 (21)
(21)
 (22)
(22)
Comparing (22) with (19), we have
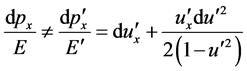 (23)
(23)
It is obvious that 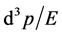 is not unchanged under the Lorentz transformation. Only when
is not unchanged under the Lorentz transformation. Only when 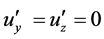 and
and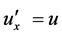 , we have
, we have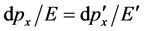 . Only by this result, we can declare that the transition probabilities of interaction processes of micro-particles have no invariability of the Lorentz transformation. Because relative speed V can be arbitrary, the factor of phase space also becomes arbitrary one. Because of
. Only by this result, we can declare that the transition probabilities of interaction processes of micro-particles have no invariability of the Lorentz transformation. Because relative speed V can be arbitrary, the factor of phase space also becomes arbitrary one. Because of  when
when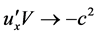 , the difference between two reference frames may be great. For the concrete calculation, according to (7), we have
, the difference between two reference frames may be great. For the concrete calculation, according to (7), we have
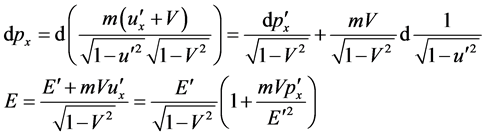 (24)
(24)
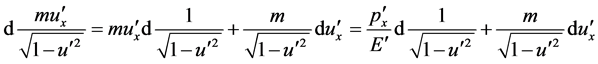 (25)
(25)
We obtain
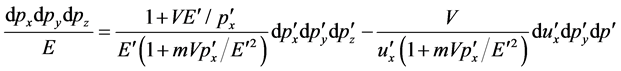 (26)
(26)
By using the Jacobi’s formula, we get
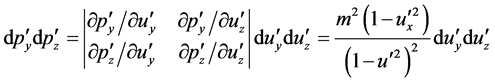 (27)
(27)
here . Suppose that the integrand function is unchanged with
. Suppose that the integrand function is unchanged with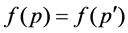 , we get
, we get
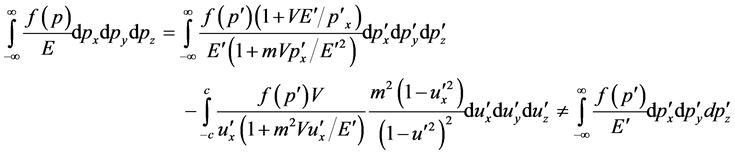 (28)
(28)
The up and down limits of integral signals about 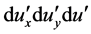 are
are![]() . The reason is that when
. The reason is that when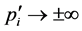 , we have
, we have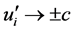 .
.
3. The Lorentz Transformations of the Motion Equation of Spinor Field and the Hamiltonian of Electromagnetic Interaction
3.1. The Lorentz Transformation Matrix of Four-Dimensional Space-Time Coordinates
In special relativity, we take 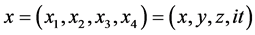 and write (3) as
and write (3) as  with
with
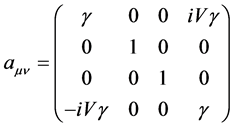 (29)
(29)
here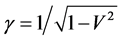 . The inversed transformation (4) is
. The inversed transformation (4) is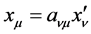 . According to the invariability principle of light’s speed, we have
. According to the invariability principle of light’s speed, we have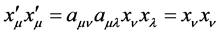 , so we have
, so we have 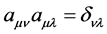 [2] . We should pay attention to the positions of indexes. According to (29), we have
[2] . We should pay attention to the positions of indexes. According to (29), we have 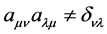 or
or 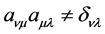 when
when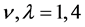 . By writing them out clearly, we have
. By writing them out clearly, we have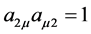 ,
, 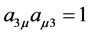 and
and
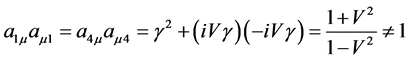 (30)
(30)
The others are zero. This result is very significant for our discussions below. It is proved that what appears in the Lorentz transformation of propagation functions of spinor fields is 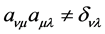 when
when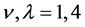 . But in the current calculation, we take
. But in the current calculation, we take . The confusion of subscript’s position leads to wrong result, so that we think that propagation functions of spinor fields is Lorentz invariable.
. The confusion of subscript’s position leads to wrong result, so that we think that propagation functions of spinor fields is Lorentz invariable.
3.2. The Lorentz Transformations of Spinor Field and Its Motion Equation
The Dirac equation of free spinor field in  reference frame is
reference frame is
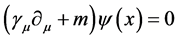 (31)
(31)
By transforming it to ![]() reference frame and considering
reference frame and considering , we have following differential relations [2]
, we have following differential relations [2]
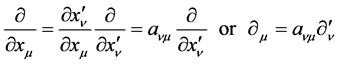 (32)
(32)
It indicates that the covariant rule of differential operator 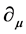 is the same as that of coordinate transformation
is the same as that of coordinate transformation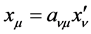 . Substituting (32) in (31) and let
. Substituting (32) in (31) and let 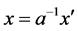 represent
represent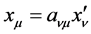 , we get
, we get
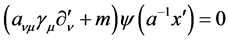 (33)
(33)
By introducing matrix 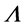 and acting it on the left side of (33), we get
and acting it on the left side of (33), we get
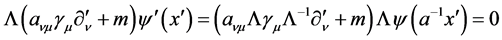 (34)
(34)
Suppose that there exists reversal matrix ![]() and let
and let
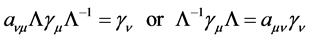 (35)
(35)
It has been proved 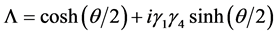 with
with  and
and 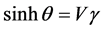 in quantum theory of field [2] . Defining new wave function
in quantum theory of field [2] . Defining new wave function 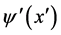 with
with
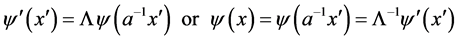 (36)
(36)
we can write (31) as
 (37)
(37)
(37) and (31) have the same form, so we say that the motion equation of free spinor field is invariable under the Lorentz transformation. On the other hand, it has been proved 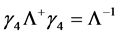 in quantum theory of field [1] . Based on it, we get
in quantum theory of field [1] . Based on it, we get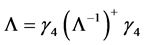 . By considering relation
. By considering relation 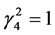 and (36), we obtain
and (36), we obtain
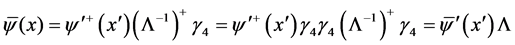 (38)
(38)
3.3. The Lorentz Transformation of the Hamiltonian of Electromagnetic Interaction
In quantum theory of field, by considering the interaction between electromagnetic field and spinor field, the motion equation in 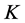 reference frame is
reference frame is
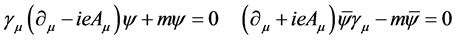 (39)
(39)
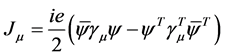
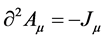 ℋ
ℋ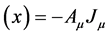 (40)
(40)
Here ℋ(x) is the Hamiltonian of interaction. According to the covariant rule of vector in special relativity, similar to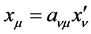 , the transformation of four-dimensional electromagnetic potential
, the transformation of four-dimensional electromagnetic potential 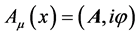 is [3]
is [3]
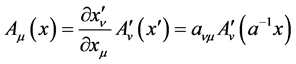 (41)
(41)
We write out the concrete results
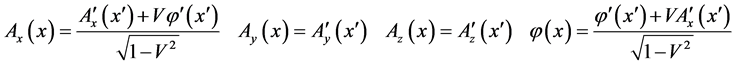 (42)
(42)
The reversed transformation of (41) is
 (43)
(43)
It is similar to 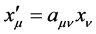 with concrete forms
with concrete forms
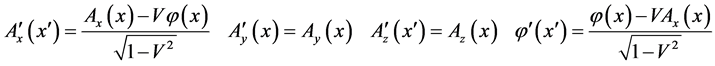 (44)
(44)
The motion equation (39) of non-free spinor particle contains the item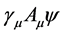 . By producing
. By producing 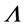 it on the left side and considering (35), (36) and (41), we get
it on the left side and considering (35), (36) and (41), we get
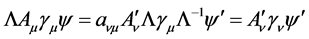 (45)
(45)
So the motion equation of non-free spinor particle is Lorentz invariable. Similarly, considering (35), (36), (38) and (41), we get
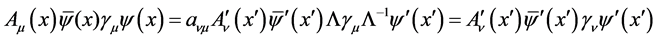 (46)
(46)
The Hamiltonian of electromagnetic interaction is also invariable under Lorentz transformation.
3.4. The Lorentz Transformations of Basic Equation of Perturbation and the Normalization Formula of Probability Wave
However, in quantum theory of field, we calculate particle’s transition probabilities in interaction representation. The basic equation of perturbation used practically is [2]
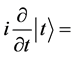 ℋ
ℋ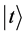 (47)
(47)
In fact, the probability amplitude 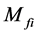 in (1) and (2) are deduced based on (47). It is easy to see that (47) has no invariability even though the interaction Hamiltonian is unchanged under the Lorentz transformation. The reason is that operator
in (1) and (2) are deduced based on (47). It is easy to see that (47) has no invariability even though the interaction Hamiltonian is unchanged under the Lorentz transformation. The reason is that operator 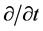 cannot keep unchanged. According to (32), let
cannot keep unchanged. According to (32), let 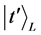 represent the Lorentz transformation of
represent the Lorentz transformation of , the Lorentz transformation of (47) is.
, the Lorentz transformation of (47) is.
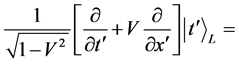 ℋ
ℋ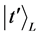 (48)
(48)
Using (48) to do calculation, the transition probability is certainly different from that based on (47). In fact, even for the most foundational normalization formula of probability wave in quantum theory of field and quantum mechanics, there is no invariability of Lorentz transformation with
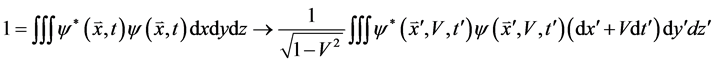 (49)
(49)
Unfortunately, these problems are neglected at present.
4. The Lorentz Transformations of Commutation Relations of Field Operators and Propagation Functions
4.1. The Lorentz Transformations of Commutation Relations and Propagation Functions of Scalar Fields
In quantum theory of field, the operators of scalar fields can be written as
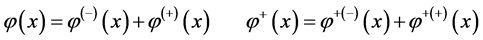 (50)
(50)
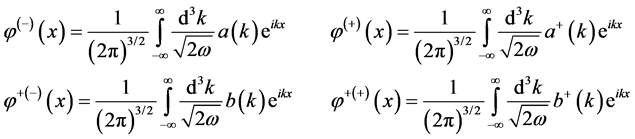 (51)
(51)
Their commutation relations are
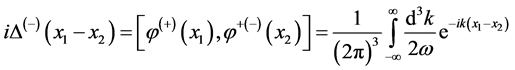 (52)
(52)
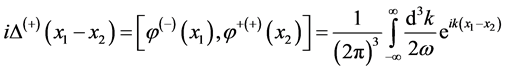 (53)
(53)
As mentioned before, 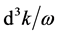 is not Lorentz invariable quantity, so the commutation relations of scalar fields have no Lorentz symmetries. The propagation function of scalar field is
is not Lorentz invariable quantity, so the commutation relations of scalar fields have no Lorentz symmetries. The propagation function of scalar field is
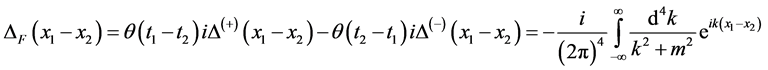 (54)
(54)
According to (17), 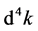 is invariable under Lorentz transformation. The other quantities in (54) are Lorentz invariable. So the propagation functions of scalar fields are unchanged under the Lorentz transformation. The situations of electromagnetic field are similar to scalar fields (with
is invariable under Lorentz transformation. The other quantities in (54) are Lorentz invariable. So the propagation functions of scalar fields are unchanged under the Lorentz transformation. The situations of electromagnetic field are similar to scalar fields (with ). The commutation relations have no symmetries but the propagation functions have under Lorentz transformations.
). The commutation relations have no symmetries but the propagation functions have under Lorentz transformations.
4.2. Lorentz Transformations of Commutation Relations and the Propagation Functions of Spinor Fields
In quantum theory of field, the operators of spinor fields can be written as
 (55)
(55)
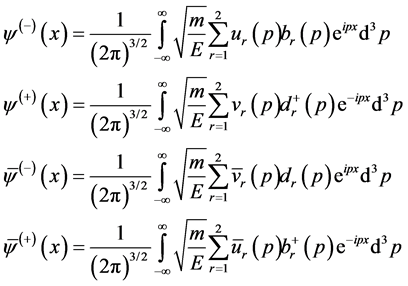 (56)
(56)
The commutation relations are
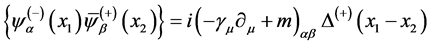 (57)
(57)
 (58)
(58)
Here 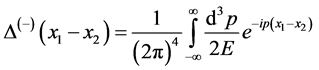 (59)
(59)
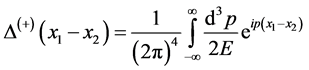 (60)
(60)
By transforming them to moving reference frame, according to (36) and (38), we have 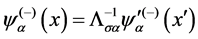 and
and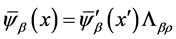 . Let
. Let  represent the direct Lorentz transformation of (57), by considering (32), we have
represent the direct Lorentz transformation of (57), by considering (32), we have
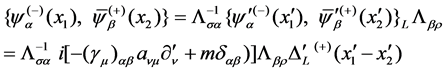 (61)
(61)
here 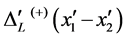 is the Lorentz transformation of
is the Lorentz transformation of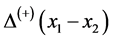 . According to (35) and by considering
. According to (35) and by considering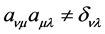 , we have
, we have
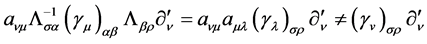 (62)
(62)
(61) becomes
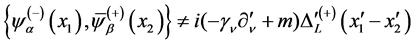 (63)
(63)
Similarly, the transformation of (58) is
 (64)
(64)
However, in the current quantum mechanics of field, we take  and lead to wrong result
and lead to wrong result 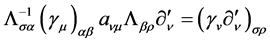 [2] . In addition, by considering the Lorentz transformation of phase factor
[2] . In addition, by considering the Lorentz transformation of phase factor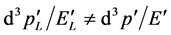 , we have
, we have
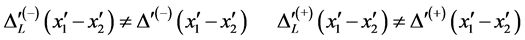 (65)
(65)
The commutation relations of spinor fields have no Lorentz symmetry too. The propagation function of spinor field is defined as
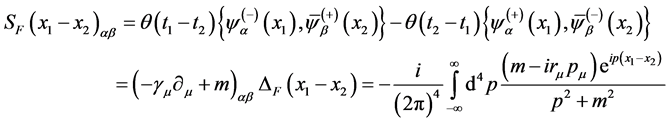 (66)
(66)
Here 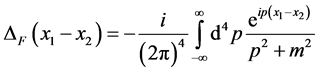 (67)
(67)
Set 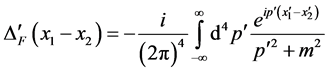 (69)
(69)
According to (63) and (64), the Lorentz transformation of spinor field is
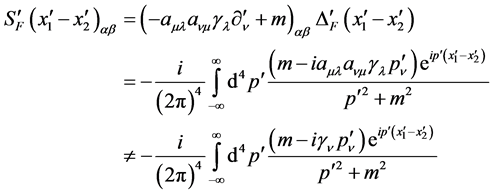 (70)
(70)
Therefore, the propagation function of spinor field has no invariability of Lorentz transformation too.
5. The Lorentz Transformation of Probability Amplitudes in Low Order Processes in Quantum Theory of Field
5.1. The Lorentz Transformation of First Order Decay Processes
The first order process describes particle’s decay in quantum theory of field. In the formula (1),  is particle’s energy. Because
is particle’s energy. Because 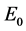 is not invariable quantity under Lorentz transformation, (1) is not invariable too. In fact, the relation between particle’s life and decay probability is
is not invariable quantity under Lorentz transformation, (1) is not invariable too. In fact, the relation between particle’s life and decay probability is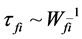 . According to special relativity, time is depends on reference frame. In the reference frame in which particle is at rest, particle’s life is longest. Only by this fact, we can say that the decay processes of micro-particles have no symmetry of Lorentz transformation. In addition,
. According to special relativity, time is depends on reference frame. In the reference frame in which particle is at rest, particle’s life is longest. Only by this fact, we can say that the decay processes of micro-particles have no symmetry of Lorentz transformation. In addition, 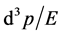 is not invariable quantity which also leads to the symmetry violation of Lorentz transformation in the first order decay process.
is not invariable quantity which also leads to the symmetry violation of Lorentz transformation in the first order decay process.
5.2. The Lorentz Transformation of Second Order Collision Processes
The transition probability of second order collision process is described by (2). Because the propagation function of spinor field has no invariability of Lorentz transformation, the probability amplitude  containing the propagation lines of Fermion violates the symmetry of Lorentz transformation. For example, for the Compton scatting process
containing the propagation lines of Fermion violates the symmetry of Lorentz transformation. For example, for the Compton scatting process
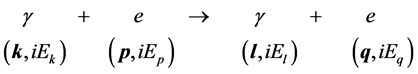
the transition probability amplitude is [2]
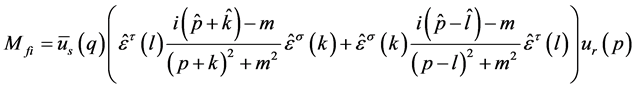 (71)
(71)
here 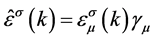 is Lorentz invariable, but
is Lorentz invariable, but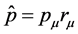 ,
, 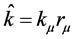 and
and 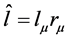 which come from the propagation function of electron have no symmetries of Lorentz transformation. We have
which come from the propagation function of electron have no symmetries of Lorentz transformation. We have
 (72)
(72)
and so do for  and
and![]() . So we have
. So we have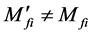 . The second process of Compton scatting has nor relativity. For the second order process containing the propagation line of bosons, for example, the scatting process between electrons,
. The second process of Compton scatting has nor relativity. For the second order process containing the propagation line of bosons, for example, the scatting process between electrons, 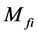 is symmetric under Lorentz transformation. But in the more high order processes of electron’s scatting, the propagation line of fermion will appear. The processes still have no symmetry of Lorentz transformation.
is symmetric under Lorentz transformation. But in the more high order processes of electron’s scatting, the propagation line of fermion will appear. The processes still have no symmetry of Lorentz transformation.
6. The Lorentz Transformations of Interactions between Bound State’s Particles
6.1. The Motion Equations of Bound Particles
According to present classification, the theories of micro-physics are divided into relativity quantum theory of field and non-relativity approximated quantum mechanics. Quantum theory of field describes unstable particles with high moving speed, mainly used in the interaction processes between elementary particles which are free at their initial and final states. The interaction Hamiltonians can be constructed by using the wave functions of free particles. As shown in (14) and (15), the wave function of free particle is invariable under Lorentz transformation. The amplitudes of transition probabilities can also be represented by the products of four-dimensional energy momentums of free particles just 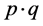 which are the invariable quantity of Lorentz transformation.
which are the invariable quantity of Lorentz transformation.
However, fundamental particles physics is only a branch of physics. These particles are created in laboratory and then decay immediately. So quantum theory of field can only dealt a small part of physics which has no closed relation with real world. What closely connected to practical world is the interaction between bound particles, for example, atoms emitting photos, superconductors and condensed matter and so on. In these problems, the interaction Hamiltonians cannot be constructed by free particle’s wave functions. For non-free particles, we have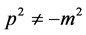 . The product
. The product 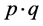 is not the invariable quantity of the Lorentz transformation. The method of quantum theory of field may not be effective in general.
is not the invariable quantity of the Lorentz transformation. The method of quantum theory of field may not be effective in general.
Non-relativity quantum mechanics describe stable particles with low moving speed. However, the principle of relativity has no approximation. It is either tenable or not tenable. If it is tenable, it should hold for the particles moving in low speeds. In fact, the principle of relativity is considered to be tenable in classical Newtonian mechanics. The formulas of the Newtonian mechanics are considered unchanged under the Galileo’s transformation. The motion equations of non-relativity quantum mechanics cannot keep unchanged under the Lorentz transformation. Can it be invariable under the Galileo’s transformation? The answer is neglected. For example, the Schrodinger’s equation is
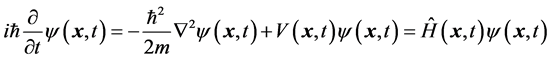 (73)
(73)
It is not invariable no matter for the Lorentz transformation or the Galileo’s transformation. So generally speaking, quantum theories of common micro-physics have no relativity. So-called the non-relativity of bound particle’s motion equations is not due to the approximate description methods we used. The essence is that they have no relativity at all!
We take electron’s scatting in eternal field, fine structure of hydrogen atomic energy level and light’s emission and absorption in bound atoms as examples to prove this conclusion below. The free particle’s Dirac equation of quantum mechanics is based on special relativity and invariable under Lorentz transformation. However, it becomes non-relativity when it is used to describe the energy levels of bound hydrogen atoms.
6.2. The Lorentz Transformation of Electron’s Scatting in External Field
Suppose that the external field is static electric field with form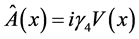 . The interaction Hamiltonian is
. The interaction Hamiltonian is
ℋ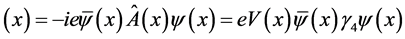 (74)
(74)
(74) is not the Lorentz invariable quantity. Based on it, it is proved in quantum theory of field that the effective scatting section is [1]
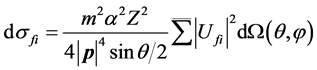 (75)
(75)
The transition probability amplitude is
 (76)
(76)
here 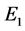 and
and 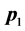 are the energy and momentum of incident particle and
are the energy and momentum of incident particle and 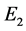 and
and 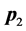 are that of outgoing particle. We have
are that of outgoing particle. We have
 (77)
(77)
By transforming (77) to moving reference frame, we have
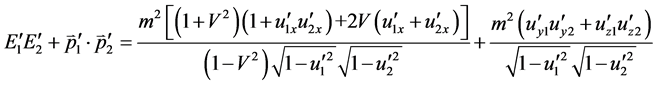 (78)
(78)
So (78) is not the Lorentz invariable quantity. In addition, phase space factor is not unchanged, so (75) has no relativity.
6.3. The Lorentz Transformation of Fine Energy Level Structure of Hydrogen Atom
It is obvious that the energy levels of hydrogen atom cannot be calculated by quantum theory of field, though it can be used to calculate the high order revision (Lams shift). By considering relativity quantum mechanics, the motion equation of an electron in hydrogen atom is
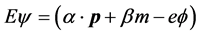 (79)
(79)
here 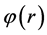 is electron’s potential function. Dirac used (79) to do calculation and obtained the formula of fine structure of hydrogen atomic energy level [4]
is electron’s potential function. Dirac used (79) to do calculation and obtained the formula of fine structure of hydrogen atomic energy level [4]
 (80)
(80)
However, 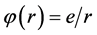 is not the Lorentz invariability quantity with
is not the Lorentz invariability quantity with
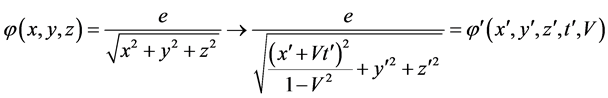 (81)
(81)
After transformation, the potential is related to speed and time. It is impossible for us to obtain the energy levels if we do calculation in ![]() reference frame by using
reference frame by using 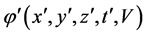 as potential. So the fine structure of hydrogen atomic energy level has no relativity.
as potential. So the fine structure of hydrogen atomic energy level has no relativity.
6.4. The Lorentz Transformation of Light’s Emission and Absorption in Bound Atoms
In the radiant process of common material, interaction between electromagnetic wave and bound electron in atom is involved. Suppose that electromagnetic wave transits along  axis, according to non-relativity quantum mechanics, the interaction Hamiltonian is [5]
axis, according to non-relativity quantum mechanics, the interaction Hamiltonian is [5]
 (82)
(82)
here free plane wave 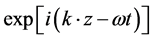 is Lorentz invariable, but operator
is Lorentz invariable, but operator 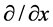 is not. According to the (32), its transformation is
is not. According to the (32), its transformation is
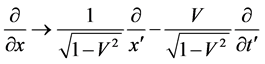 (83)
(83)
The operator is acted on the wave function of bound electron and the bound wave function is not Lorentz invariable. The result has no symmetry of Lorentz transformation. Similarly, (82) is not invariable under the Galileo’s coordinate transformations. No mater from what angle, the processes of light’s emission and absorption have no relativity too.
In fact, for most practical problems of micro-physics, we cannot use the method of relativity quantum theory of field to deal with. We can only calculate them by non-relativity quantum mechanics. Under the conditions of low speeds, these methods are very effective. We cannot say they are imprecise. More important is that these problems have no the symmetries of Lorentz transformation in essence, we cannot impose relativity on them.
7. The Lorentz Transformations of High Order Perturbations Normalization Processes in Quantum Theory of Field
7.1. The Lorentz Transformation of Lamb Shift
The high order perturbation processes of quantum theory of fields contain infinite and need to be renormalized. The normalization may introduce the symmetry violation of Lorentz transformation. At first, we take the Lamb shift of hydrogen atom’s energy levels as examples. By the normalization calculation, the Lamb shift is [6]
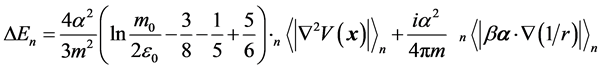 (84)
(84)
here 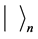 is the wave function of bound electron in hydrogen atom. For the ground state’s electron, we have
is the wave function of bound electron in hydrogen atom. For the ground state’s electron, we have
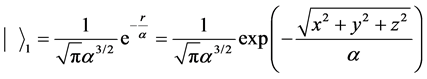 (85)
(85)
By transforming it to moving reference frame, we get
 (86)
(86)
New wave function depends on time and relative speed without Lorentz invariability. Operators 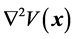 and
and  are not invariable too. Both average values
are not invariable too. Both average values and
and 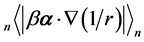 are not symmetrical under the Lorentz transformation. So the Lamb shift has no relativity.
are not symmetrical under the Lorentz transformation. So the Lamb shift has no relativity.
7.2. The Lorentz Symmetry Violations Caused by Integral Transformations
In the normalization processes of high order perturbations, following integrals are involved
 (87)
(87)
here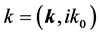 ,
, 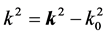 and
and . As we known that
. As we known that 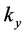 and
and 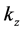 are Lorentz invariable, bud
are Lorentz invariable, bud  and
and  are not. By using the Jacobi’s formula, we have
are not. By using the Jacobi’s formula, we have
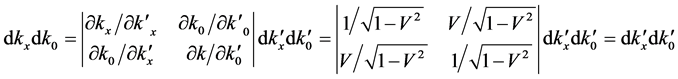 (88)
(88)
So 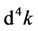 is still the invariable quantity of Lorentz transformation. Because
is still the invariable quantity of Lorentz transformation. Because 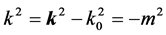 is also Lorentz invariable, (87) is unchanged under the Lorentz transformation.
is also Lorentz invariable, (87) is unchanged under the Lorentz transformation.
However, the direct calculation of (87) is difficult. In order to complete the integrals, we need to move the original point of coordinate, then introduce transformation  and obtain
and obtain 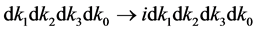 as well as
as well as 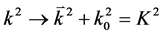 . By introducing four-dimensional spherical coordinates [4]
. By introducing four-dimensional spherical coordinates [4]
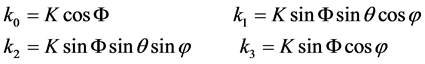 (89)
(89)
we get
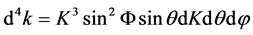 (90)
(90)
In this way, for same simple situations, (87) can be integrated. For example
 (91)
(91)
Let  is the Lorentz transformation of
is the Lorentz transformation of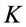 , we have
, we have
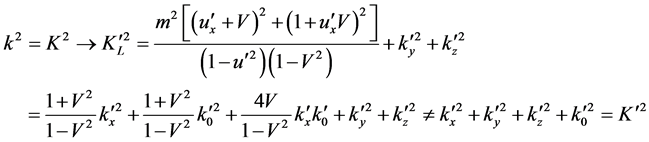 (92)
(92)
So 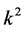 is not the invariable quantity of Lorentz transformation, (87) and (91) are not invariable again. Because (87) and (91) appears in the common normalization processes of high order perturbations commonly, the calculation methods of normalizations violate the Lorentz invariability generally. Let’s take several examples below.
is not the invariable quantity of Lorentz transformation, (87) and (91) are not invariable again. Because (87) and (91) appears in the common normalization processes of high order perturbations commonly, the calculation methods of normalizations violate the Lorentz invariability generally. Let’s take several examples below.
7.3. The Lorentz Transformation of Mass Normalization
The probability amplitude of mass normalization is [6]
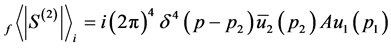 (93)
(93)
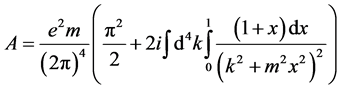 (94)
(94)
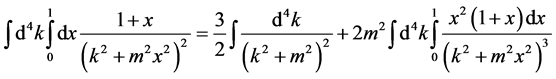 (95)
(95)
By introducing 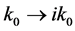 and considering
and considering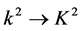 , we have
, we have
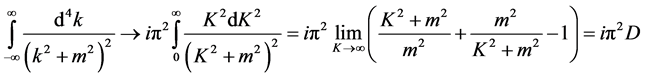 (96)
(96)
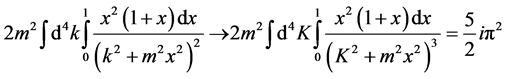 (97)
(97)
 in (96) is linearly infinite, but (97) is finite. Because
in (96) is linearly infinite, but (97) is finite. Because  is Lorentz invariable, but
is Lorentz invariable, but  is not according to (92), we have
is not according to (92), we have
 (98)
(98)
 (99)
(99)
The probability amplitude of mass normalization has no invariability of Lorentz transformation.
7.4. The Lorentz Transformation of Vacuum Polarization
The probability amplitude of vacuum polarization is [6]
 (100)
(100)
 (101)
(101)
 (102)
(102)
here  is infinite, we have
is infinite, we have
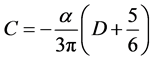 (103)
(103)
By taking several simplifications, including
 (104)
(104)
we obtain
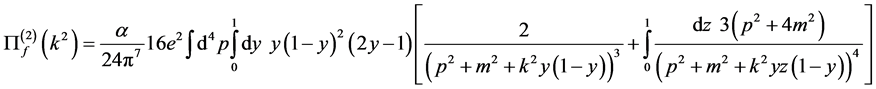 (105)
(105)
Let 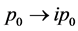 and
and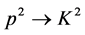 , the integral of (105) is
, the integral of (105) is
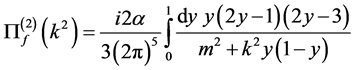 (106)
(106)
Similarly, because 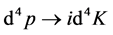 is invariable but
is invariable but  is not under the Lorentz transformation. So (105) is not invariable. We cannot obtain (106) from (105) after Lorentz transformation. Besides, (102) contains
is not under the Lorentz transformation. So (105) is not invariable. We cannot obtain (106) from (105) after Lorentz transformation. Besides, (102) contains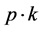 . If we take
. If we take 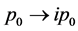 in (102), correspondingly, we should let
in (102), correspondingly, we should let 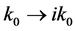 in (105), so that
in (105), so that 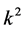 in (105) and (106) is not Lorentz invariable again. But this point was neglected in the current theory of normalization.
in (105) and (106) is not Lorentz invariable again. But this point was neglected in the current theory of normalization.
7.5. The Lorentz Transformation of Third Order Vertex Angle Process
The amplitude of third order vertex angle process is [6]
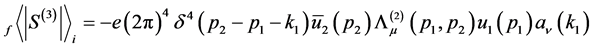 (107)
(107)
Set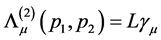 , we get
, we get
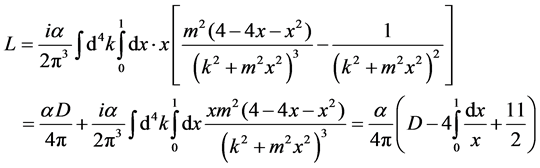 (108)
(108)
Similarly, 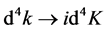 is Lorentz invariable but
is Lorentz invariable but  is not. We have
is not. We have
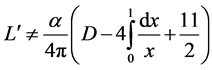 (109)
(109)
The normalization of the third order vertex angle process is not invariable under Lorentz transformation.
It notes that this kind of symmetry violation is caused by the calculation method of integral transformation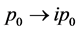 . If we do not introduce this transformation, there is no symmetry violation. We should to ask whether or not the symmetry violation is essential? The problem is that if we do not let
. If we do not introduce this transformation, there is no symmetry violation. We should to ask whether or not the symmetry violation is essential? The problem is that if we do not let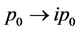 , the integral cannot be completed so that concrete results cannot be obtained to compare with experiments. We should consider the integral transformation as a part of normalization calculation. Because the results of normalizations are consistent with experiments, in this meaning, we may say that the calculation method which leads to Lorentz symmetry violation has the practical meaning in physics.
, the integral cannot be completed so that concrete results cannot be obtained to compare with experiments. We should consider the integral transformation as a part of normalization calculation. Because the results of normalizations are consistent with experiments, in this meaning, we may say that the calculation method which leads to Lorentz symmetry violation has the practical meaning in physics.
In summary, three basic normalizations processes of electromagnetic interaction violate the symmetry of Lorentz transformation. The conclusion is also suitable for other interaction theories.
8. Discussion
By the analysis above, we see that the principle of relativity cannot hold in the interaction theories of microparticles at all! But why physicists did not find this problem up to now? This question is worthy of our thought.
When Einstein put forward special relativity in 1905, science community has not yet reached common understanding about whether or not atoms exist, not to mention quantum mechanics and elementary particle physics. It was the matter after relativity was accepted widely when it was applied in elementary particle physics. Physicists believed relativity was correct, so that Lorentz symmetry violation in micro-physics was neglected consciously or unconsciously. Speaking in other words, the problems of Lorentz symmetry violations in microparticle physics were handled vaguely. However, as long as we get to the bottom of matter, the problems still emerge from the water.
In special relativity, the invariability principle of light’s speed and the principle of relativity are independent each other. But in some situations, they are connected. The Lorentz formula is deduced based on the invariability principle of light’s speed. According to the principle of relativity, the Lorentz formula has relative significance only. Meanwhile, the principle of relativity declares that the forms of physical motion equations do not change with reference frames. To reach this aim, physical quantities should be transformed in covariant forms. As shown in (41) and (42), covariance is for general physical quantities and Lorentz transformation is for space-time coordinate. Both are different concepts, but we often do not distinguish them.
Besides, in order to keep the motion equation of spinor field unchanged, we should introduce spinor transformation. However, as shown in (36), spinor transformation is not covariant. That is to say, in order to make the motion equation of quantum mechanics unchanged, covariance is not enough. The problem is very complex actually. It is proved in this paper that even though spinor transformation is considered, the interaction theories of micro-particles have yet no relativity.
On the other hand, the invariability principle of light’s speed has obtained a lot of verifications, especially in the experiments of high energy accelerators. For example, the experiment to measure light’s speed in the process that high energy proton decays into meson and photon in CERN in 1964. However, the principle of relativity is only a kind of belief without really strict verification. Because common experiments only involve low speed motions, similar to Galileo, modern physicists make their judgments according to common experiments. They belies that the principle of relativity is alright.
So the real situations may be that the effectiveness of the invariability principle of light’s speed coves the ineffectiveness of the principle of relativity. In fact, up to now days, physicists have never made practical measurements in the moving reference frame with high enough speed to verify the principle of relativity. The Michelson interference experiment seems to prove that the absolute motion of the earth cannot be measured. However, in relativity, we use the invariability of light’s speed to explain the Michelson interference experiment. In this meaning, the Michelson interference experiment only verifies the invariability principle of light’s speed, without verifying the principle of relativity.
Ironically, many pioneers of relativity including Michelson, Lorentz, Poincare and March and so on did not accept Einstein’s relativity. What they opposed was the principle of relativity, rather than the invariability principle of light’s speed. The reason was that the principle of relativity leads to various logic paradoxes. In fact, it is the problem of experiment whether or not the invariability principle of light’s speed can hold. If there is no the principle of relativity, we can still reach the Lorentz transformation based on the invariability principle of light’s speed. In this case, the Lorentz transformation becomes absolute, just as Lorentz himself considered it. All formulas of special relativity are still effective, but become absolute ones. The effects of special relativity also become absolute ones.
However, it is mainly a logic problem whether or not the principle of relativity is tenable. So it is easy to cause arguments. Since Einstein established special relativity one hundred years ago, criticism has never stopped. The arguments are so violent and last so long time that it is unwonted in the history of science. The arguments are concentrated on the space-time paradox problems just as length paradox and time paradox which are often specious. Correctness and mistakes are mixed together so that it is difficult to obtain correct judgment. Because these problems do not belong to the main stream of physical research at present time, physicists do not pay attention to them again.
A dramatic change appeared in 1960’s when CMBR was founded. The isotropy of CMBR provided a choice of absolutely static reference frame for physics. The principle of relativity is not a problem of logic again. It became a problem which can be verified through experiments and observation of astronomy. In fact, the Sagnac effect found in 1912 had indicated that the relativity of motion was impossible. The time comparison experiments of microwave communications through satellite between Xian and Tokay achieved in 2001 also revealed the same conclusion [7] . But what can really provide an absolutely static reference frame for physics is just the isotropy of CMBR. Because it contradicts the relativity principle of motion directly, physics is in an awkward position at present.
On the other hand, all arguments about relativity principle such as space-time paradox, Sagnac effect, and the isotropy of CMBR are macro-phenomena. But macrocosm is composed of micro-particles. If the physical laws of micro-particles have relativity, physicists have reason to believe the principle of relativity. But if the physical laws of micro-particles have no invariability under the Lorentz transformations, physicists have no reason to stick to the relativity principle of motion again.
The proofs in this paper are clear and certain without any speciousness. So there is only a way for physics. That is to give up the principle of relativity but reserve the invariability principle of light’s speed. In this way, all formulas of special relativity can be reserved but we need to explain them in absolute forms. The author will discuss this problem later.
About three hundred years ago, Newton established classical mechanics. Newton thought that absolute space existed, but he did not know where it was. Modern cosmology found absolute reference frame for physics. Particle physics will also provide its judgment for absolute motion. Both macro-physics and microphysics reach united conclusion again.
References
- Chou, G.X. (1980) Introduce to Quantum Theory of Field. Science Publishing Company, Beijing, 125, 166, 171, 203.
- Luo, C.X. (1986) Introduce to Quantum Theory of Field. Publishing Company of Shanxi Normal University, Xi’an, 136, 137, 143.
- Cai, S.S. and Hu, Y. (1985) Classical Electrodynamics. Publishing Company of Fudan University, Shanghai, 398.
- Zhou, J.Y. (1986) Quantum Mechanics. Science Publishing Company, Beijing, 602.
- Zhou, S.X. (1962) Quantum Mechanics. High Education Publishing Company, Beijing, 239.
- Zhu, H.Y. (1960) Quantum Theory of Field. Science Publishing Company, Beijing, 228, 259, 298, 300, 305.
- Sun, H.W. and Li, Z.G. (2001) Space Navigation Measurement Technology. 55-58.

