Journal of Modern Physics
Vol.5 No.11(2014), Article
ID:47492,14
pages
DOI:10.4236/jmp.2014.511105
Measuring Mass and Spin of Dark Matter Particles with the Aid Energy Spectra of Single Lepton and Dijet at the 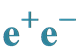 Linear Collider
Linear Collider
I. F. Ginzburg1,2
1Sobolev Institute of Mathematics, Novosibirsk, Russia 2Novosibirsk State University, Novosibirsk, Russia
Email: ginzburg@math.nsc.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 January 2014; revised 18 February 2014; accepted 16 March 2014
ABSTRACT
In many models stability of Dark Matter particles 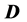 is ensured by conservation of a new quantum number referred to as
is ensured by conservation of a new quantum number referred to as 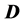 -parity. Our models also contain charged
-parity. Our models also contain charged 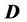 -odd particles
-odd particles 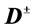 with the same spin as
with the same spin as . Here we propose a method to precisely measure the masses and spins of
. Here we propose a method to precisely measure the masses and spins of 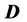 -particles in the process
-particles in the process 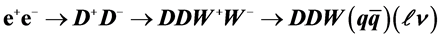 with a signature dijet
with a signature dijet 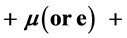 nothing. It is shown that the energy distribution of the lepton has singular points (upper edge and kinks or a peak) whose positions are kinematically determined. For precise determination of
nothing. It is shown that the energy distribution of the lepton has singular points (upper edge and kinks or a peak) whose positions are kinematically determined. For precise determination of 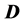 and
and 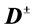 masses, it is sufficient to measure these singular points and upper edge of dijet energy spectrum. After this procedure, even an approximate measurement of the corresponding cross section allows a determination of the spin of
masses, it is sufficient to measure these singular points and upper edge of dijet energy spectrum. After this procedure, even an approximate measurement of the corresponding cross section allows a determination of the spin of 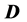 particles to be performed. New points of this work are: 1) We propose to use only the well measurable energy spectra of individual leptons and the upper edge of the dijet energy spectrum. 2) We propose to identify the spin of
particles to be performed. New points of this work are: 1) We propose to use only the well measurable energy spectra of individual leptons and the upper edge of the dijet energy spectrum. 2) We propose to identify the spin of 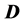 -particles via value of the cross section for the discussed process.
-particles via value of the cross section for the discussed process.
Keywords:Dark Matter, W-Boson, Lepton, Linear Collider

1. Introduction
1.1. Models
In the broad class of models Dark Matter (DM) consists of particles  similar to those in SM, with the following properties:
similar to those in SM, with the following properties:
• The neutral DM particle 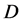 with mass
with mass 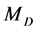 and spin
and spin 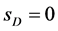 or
or 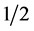 has a new conserved quantum number, which we call the
has a new conserved quantum number, which we call the 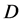 -parity. All known particles are
-parity. All known particles are 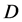 -even, while the
-even, while the 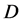 is
is 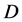 -odd.
-odd.
• In addition to , other
, other 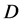 -odd particles exist: a charged
-odd particles exist: a charged 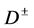 and (sometimes) a neutral
and (sometimes) a neutral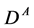 , with the same spin
, with the same spin 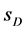 and with masses
and with masses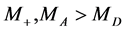 . The
. The  -parity conservation ensures stability of the lightest
-parity conservation ensures stability of the lightest  -odd particle
-odd particle .
.
• These 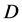 -particles interact with the SM particles via the Higgs boson
-particles interact with the SM particles via the Higgs boson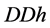 ,
, 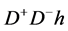 ,
, 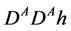 and via the covariant derivative in the kinetic term of the Lagrangian. These are the gauge interactions
and via the covariant derivative in the kinetic term of the Lagrangian. These are the gauge interactions ,
,  ,
, 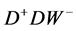 ,
, 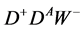 ,
,  with the standard electroweak couplings
with the standard electroweak couplings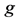 ,
, 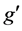 and
and 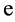 (coupling to
(coupling to 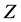 can be added by a mixing factor
can be added by a mixing factor , deviation from 1 appears due to possible mixing of
, deviation from 1 appears due to possible mixing of 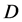 with other
with other 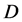 -odd neutrals).
-odd neutrals).
 The first example of such model provides well known MSSM (see e.g. [1] -[6] ) for specific set of parameters. Here our term
The first example of such model provides well known MSSM (see e.g. [1] -[6] ) for specific set of parameters. Here our term 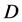 -parity means
-parity means 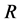 -parity. For the considered set of parameters,
-parity. For the considered set of parameters, 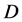 is the lightest neutralino
is the lightest neutralino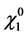 , the heavier neutralino
, the heavier neutralino 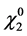 can play role
can play role 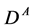 and the next in mass
and the next in mass 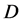 -odd particle is the lightest chargino, spin of these
-odd particle is the lightest chargino, spin of these 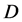 -particles
-particles . The other
. The other 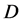 -odd particles (in particular, sleptons and squarks) are supposed to be heavier than the ILC beam energy
-odd particles (in particular, sleptons and squarks) are supposed to be heavier than the ILC beam energy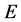 .
.
 The second example of such models provides the Inert Doublet Model (IDM) (see e.g. [7] -[13] and Appendix A). That is the
The second example of such models provides the Inert Doublet Model (IDM) (see e.g. [7] -[13] and Appendix A). That is the  symmetric Two Higgs Doublet Model, containing two scalar doublets
symmetric Two Higgs Doublet Model, containing two scalar doublets 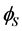 and
and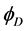 . The “standard” scalar (Higgs) doublet
. The “standard” scalar (Higgs) doublet 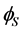 is responsible for electroweak symmetry breaking and the masses of fermions and gauge bosons just as in the Standard Model (SM). The second scalar doublet
is responsible for electroweak symmetry breaking and the masses of fermions and gauge bosons just as in the Standard Model (SM). The second scalar doublet 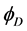 doesn’t receive vacuum expectation value and doesn’t couple to fermions. In this model the
doesn’t receive vacuum expectation value and doesn’t couple to fermions. In this model the  -parity conservation is ensured by a
-parity conservation is ensured by a  symmetry, four degrees of freedom of the Higgs doublet
symmetry, four degrees of freedom of the Higgs doublet 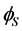 are the same as in the SM: three Goldstone modes and the standard Higgs boson
are the same as in the SM: three Goldstone modes and the standard Higgs boson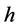 . All the components of the scalar doublet
. All the components of the scalar doublet 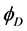 are realized as the massive
are realized as the massive 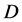 -particles: two charged
-particles: two charged 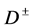 and two neutral ones
and two neutral ones ,
,  with masses
with masses ,
, 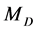 ,
,  respectively with
respectively with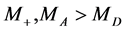 . IDM contains no other
. IDM contains no other 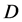 -odd particles. All
-odd particles. All 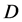 -particles have spin
-particles have spin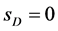 .
.
A possible value of mass 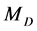 is limited by stability of
is limited by stability of 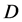 during the Universe existence [14] -[20] . The non-observation of the processes
during the Universe existence [14] -[20] . The non-observation of the processes 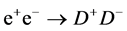 and
and 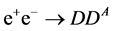 at LEP gives
at LEP gives 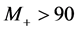 GeV and
GeV and 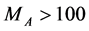 GeV (at
GeV (at 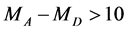 GeV) [11] -[13] . Limitations for masses of neutralino and chargino can be found in [20] . For IDM, limitations for parameters of
GeV) [11] -[13] . Limitations for masses of neutralino and chargino can be found in [20] . For IDM, limitations for parameters of 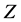 -peak,
-peak, 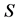 and
and 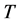 results in ([11] -[13] [20] )
results in ([11] -[13] [20] )
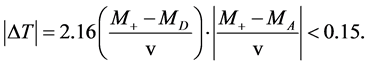 (1)
(1)
with 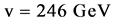 expectation value of Higgs field. Further, we will have in mind
expectation value of Higgs field. Further, we will have in mind 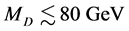 and assume
and assume  GeV.
GeV.
1.2. The Problem
The neutral and stable  can be produced and detected via production
can be produced and detected via production 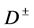 or
or 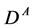 and subsequent decay
and subsequent decay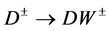 ,
, 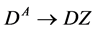 with either on shell (real) or off shell
with either on shell (real) or off shell  or
or . The off shell
. The off shell 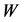 emerges as a
emerges as a 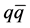 pair (dijet1) or
pair (dijet1) or , having the same quantum numbers as
, having the same quantum numbers as  but with an effective mass
but with an effective mass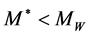 . From now on,
. From now on, 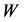 or
or 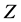 refers to any of these two cases.
refers to any of these two cases.
To discover the DM particle, one needs to specify such processes with a clear signature. The 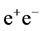 Collider ILC/CLIC provides an excellent opportunity for this task (see, e.g., [21] [22] ) in the process
Collider ILC/CLIC provides an excellent opportunity for this task (see, e.g., [21] [22] ) in the process 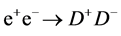 with a clear signature, see Equations (6) and (7) below. The cross section of this process is a large fraction of the total cross section of
with a clear signature, see Equations (6) and (7) below. The cross section of this process is a large fraction of the total cross section of  annihilation, Section 3.3.
annihilation, Section 3.3.
The masses 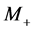 and
and 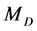 could be found via the edges of the energy distribution of dijets, originating from
could be found via the edges of the energy distribution of dijets, originating from  from decay
from decay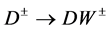 , section 2.2, 2.4 (see [5] [6] for MSSM and [11] -[13] for IDM). However, this method cannot provide a good accuracy in measuring the mass. Indeed, the individual jet energy measurement suffers from a sizable uncertainty. In particular, this uncertainty smoothes the lower edge in the dijet energy spectrum.
, section 2.2, 2.4 (see [5] [6] for MSSM and [11] -[13] for IDM). However, this method cannot provide a good accuracy in measuring the mass. Indeed, the individual jet energy measurement suffers from a sizable uncertainty. In particular, this uncertainty smoothes the lower edge in the dijet energy spectrum.
On the contrary, the lepton energy can be measured much more precisely. In this paper we show, first, that the energy distribution of leptons has singular points whose positions are kinematically determined. Measuring positions of these singularities will allow, in principle, to determine masses 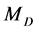 and
and  with good precision (Sections 2.3 and 2.4). In contrast to [5] -[6] [11] -[13] , our description is suitable for different models.
with good precision (Sections 2.3 and 2.4). In contrast to [5] -[6] [11] -[13] , our description is suitable for different models.
Moreover, we present a simple method for measuring spin of DM particles in these very experiments.
The discussed problem differs strongly from that for the case when the lightest charged D-odd particle is slepton (another set of parameters of MSSM). In the latter case DM particles are produced via slepton pair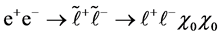 . First of all, signature of this process is quite different from that one in our problem (6), (7). Second, the energy of observable lepton decay product of slepton is measurable well in each individual event, in difference with our case, when similar product of decay,
. First of all, signature of this process is quite different from that one in our problem (6), (7). Second, the energy of observable lepton decay product of slepton is measurable well in each individual event, in difference with our case, when similar product of decay, 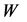 , is seen as dijet or lepton plus neutrino with badly measurable energy in each individual event. Therefore, the approach used in the analysis of slepton production (cf. [23] -[25] ) cannot be applied directly to our problem.
, is seen as dijet or lepton plus neutrino with badly measurable energy in each individual event. Therefore, the approach used in the analysis of slepton production (cf. [23] -[25] ) cannot be applied directly to our problem.
The overall picture is summarized in Section 3. Short conclusion is given in Section 4.
In the Appendix B we discuss the potential of the process 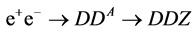 for similar problems, for completeness. In contrast with previous studies, we find that this potential is not too high.
for similar problems, for completeness. In contrast with previous studies, we find that this potential is not too high.
In the Appendix C we consider possible background processes and show that the most of them can be neglected at the analysis.
1.3. Scale of Cross Sections
We express discussed cross sections via
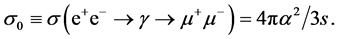 (2)
(2)
The total cross section of 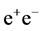 annihilation at ILC for
annihilation at ILC for  GeV is
GeV is . The annual integrated luminosity
. The annual integrated luminosity 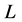 for the ILC project [22] gives
for the ILC project [22] gives
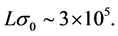 (3)
(3)
The process 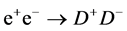 represents a significant fraction of all
represents a significant fraction of all 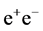 annihilation events-see (19), (20), Figure 2 and Table2 With the luminosity (3), the annual number of events of discussed type will be
annihilation events-see (19), (20), Figure 2 and Table2 With the luminosity (3), the annual number of events of discussed type will be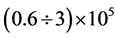 , depending on
, depending on 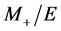 and
and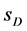 , and about
, and about 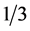 of them (in the mode with
of them (in the mode with 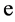 or
or 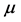 plus dijet) are suitable for our analysis.
plus dijet) are suitable for our analysis.
2. The Process 
Note before all that the energies, 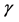 -factors and velocities of
-factors and velocities of  are
are
 (4)
(4)
2.1. The Signature
 If
If 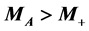 or
or 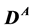 is absent, once produced, particles
is absent, once produced, particles 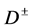 decay fast (with a unit probability) to
decay fast (with a unit probability) to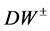 ,
,
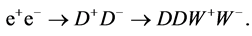 (5)
(5)
The observable states are decay products of  with a large missing transverse energy
with a large missing transverse energy 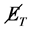 carried away by the invisible
carried away by the invisible 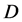 -particle, and the missing mass of particles escaping observation
-particle, and the missing mass of particles escaping observation 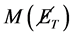 is large. In contrast to the LHC, where a large flux of low
is large. In contrast to the LHC, where a large flux of low 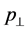 particles demands an additional
particles demands an additional  cut off, at
cut off, at  LC such particles are absent.
LC such particles are absent.
Therefore, the signatures of the process in the modes suitable for observation are
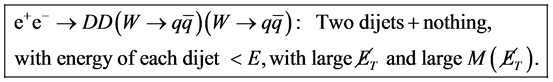 (6a)
(6a)
 (6b)
(6b)
At 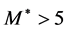 GeV, the branching ratios for different channels of
GeV, the branching ratios for different channels of  decay are roughly identical for on-shell
decay are roughly identical for on-shell  [20] and off-shell
[20] and off-shell . In particular, the fraction of events with signature (6a) is
. In particular, the fraction of events with signature (6a) is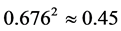 . The fraction of events with signature (6b) is
. The fraction of events with signature (6b) is  (here 0.17 is a fraction of
(here 0.17 is a fraction of 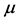 or
or 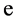 from the decay of
from the decay of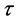 ). At
). At 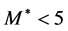 GeV,
GeV,  and
and 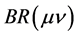 increase, while the dijet becomes a set of a few hadrons.
increase, while the dijet becomes a set of a few hadrons.
 If
If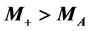 , when analysing the main process
, when analysing the main process , one more decay channel is added,
, one more decay channel is added, . Its branching ratio
. Its branching ratio 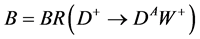 is typically less than 0.5 (see discussion in section 2.4). Particle
is typically less than 0.5 (see discussion in section 2.4). Particle 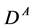 decays fast to
decays fast to , creating new cascades
, creating new cascades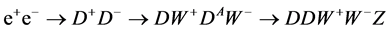 ,
,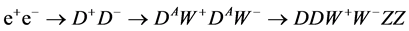 . As a result, the signature of the processes
. As a result, the signature of the processes 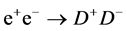 in the modes suitable for observation contains both (6) and processes with decay
in the modes suitable for observation contains both (6) and processes with decay ’s or
’s or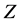 ’s in the mentioned cascades:
’s in the mentioned cascades:
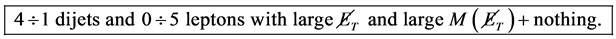 (7)
(7)
Note that the processes with invisible decay 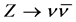 (we denote these states as
(we denote these states as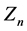 , their
, their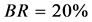 ) have signature (6).
) have signature (6).
2.2.  Energy Distribution in
Energy Distribution in 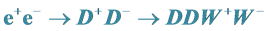
Here we consider the energy distribution of 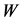 with an effective mass
with an effective mass . At each value of
. At each value of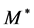 , we have in the rest frame of
, we have in the rest frame of  a two-particle decay
a two-particle decay 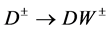 with2
with2
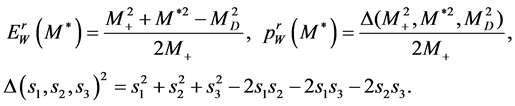 (8)
(8)
Denoting by 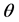 the
the 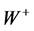 escape angle in the
escape angle in the 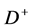 rest frame with respect to the direction of
rest frame with respect to the direction of 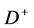 motion in the laboratory frame and using
motion in the laboratory frame and using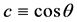 , we find the energy of
, we find the energy of 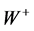 in the laboratory frame as
in the laboratory frame as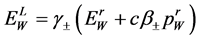 . Therefore, at given
. Therefore, at given , the energy
, the energy 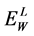 of
of 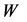 lies within the interval
lies within the interval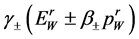 .
.
In particular, at 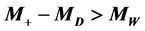 we have
we have , and the kinematical edges of the
, and the kinematical edges of the 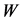 energy distribution are
energy distribution are
 (9)
(9)
At  we have
we have , and obtain similar edges, which are different for each value of
, and obtain similar edges, which are different for each value of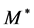 . The absolute upper and lower bounds on the energy distribution of
. The absolute upper and lower bounds on the energy distribution of 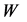 are attained at
are attained at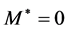 , they are equal to
, they are equal to
 (10)
(10)
At the highest value 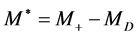 we have
we have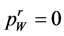 , and an interval (9) is reduced to a point, where the entire
, and an interval (9) is reduced to a point, where the entire  energy distribution has a maximum (peak) of
energy distribution has a maximum (peak) of
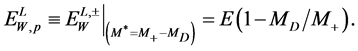 (11)
(11)
2.3. Single Lepton Energy Distribution in 
The fraction of such events for each separate lepton,  ,
,  ,
, 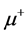 or
or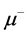 , is about 0.08, their sum is about 0.33 of the total cross section of the process. We will speak, for definiteness,
, is about 0.08, their sum is about 0.33 of the total cross section of the process. We will speak, for definiteness, 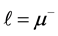 and neglect the muon mass.
and neglect the muon mass.
Note that in the laboratory frame, for a 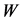 with some energy
with some energy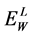 , its
, its 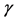 -factor and the velocity are
-factor and the velocity are 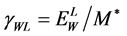 and
and .
.
We study the distribution3 of muons over its energy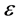 ,
,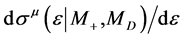 . We show that this distribution has singular points, whose positions are kinematically determined, i.e. model independent.
. We show that this distribution has singular points, whose positions are kinematically determined, i.e. model independent.
a) If  we have
we have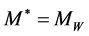 , and the muon energy and momentum in the rest frame of
, and the muon energy and momentum in the rest frame of 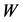 are
are . Just as above, denoting by
. Just as above, denoting by 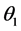 the escape angle of
the escape angle of 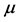 relative to the direction of the
relative to the direction of the 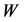 in the laboratory frame and using
in the laboratory frame and using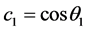 , we find that the muon energy in the laboratory frame is
, we find that the muon energy in the laboratory frame is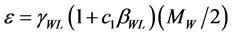 . Therefore, for these muons
. Therefore, for these muons 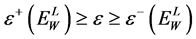 where
where
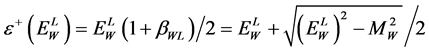 and
and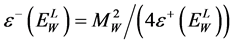 .
.
It is easy to check that the interval corresponding to energy 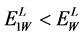 is located entirely within the interval, correspondent to energy
is located entirely within the interval, correspondent to energy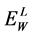 . Therefore, all muon energies lie within the interval determined by the highest value of
. Therefore, all muon energies lie within the interval determined by the highest value of 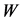 energy:
energy:
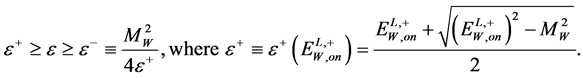 (12)
(12)
(Note that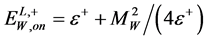 .)
.)
With a shift of 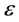 from these boundaries inwards, the density of states in the
from these boundaries inwards, the density of states in the 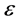 distribution grows monotonically due to contributions of smaller values
distribution grows monotonically due to contributions of smaller values  up to values
up to values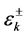 , corresponding to the lowest value of
, corresponding to the lowest value of 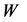 energy
energy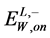 :
:
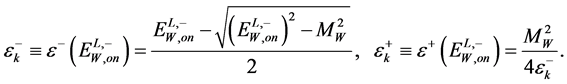 (13)
(13)
In these points the energy distributions of muons has kinks. Between these kinks, the 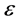 -distribution is approximately flat.
-distribution is approximately flat.
Figure 1, the left plot, shows the energy distribution of muons for the case of the matrix element independent of . Since positions of kinks are kinematically determined, it is not surprising that calculations for distinct models (containing different angular dependence) demonstrate variations in shapes but do not perturb the position of kinks.
. Since positions of kinks are kinematically determined, it is not surprising that calculations for distinct models (containing different angular dependence) demonstrate variations in shapes but do not perturb the position of kinks.
b) If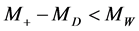 , the
, the 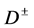 decays to
decays to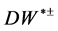 , where
, where 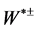 is an off-shell
is an off-shell 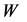 with an effective mass
with an effective mass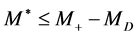 . The calculations for each
. The calculations for each 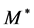 similar to shown above demonstrate that the muon energies are within the interval appearing at
similar to shown above demonstrate that the muon energies are within the interval appearing at :
:
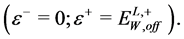 (14)
(14)
Similarly to the preceding discussion, the increase of 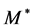 shifts the interval boundaries inwards. Therefore, the muon energy distribution increases monotonously from the outer bounds up to the maximum (peak) at
shifts the interval boundaries inwards. Therefore, the muon energy distribution increases monotonously from the outer bounds up to the maximum (peak) at 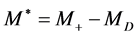 (cf. (11)):
(cf. (11)):
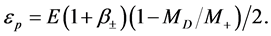 (15)
(15)
To get an idea about the shape of the peak, we use the distribution of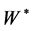 ’s (dijets or
’s (dijets or 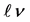 pairs) over the effective masses
pairs) over the effective masses 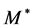 which is given by the spin-dependent factor
which is given by the spin-dependent factor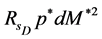 :
:
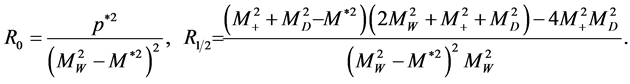 (16)
(16)
The density of muon states in energy is calculated by convolution of kinematically determined distribution with distribution (16). Neglecting the angular dependence of the matrix element, we obtain the result in form of
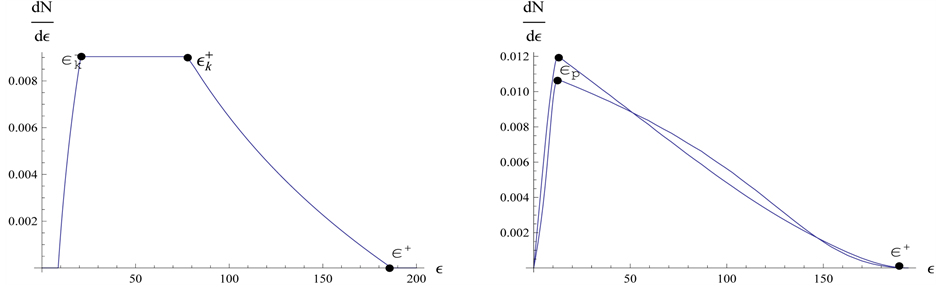
Figure 1. Distributions 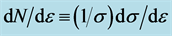 at
at 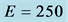 GeV,
GeV,  GeV for
GeV for 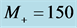 GeV—the case with
GeV—the case with 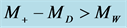 (the right plot) and for
(the right plot) and for 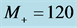 GeV—the case with
GeV—the case with  (the left plot). In the latter case, the higher and lower peaks are for
(the left plot). In the latter case, the higher and lower peaks are for 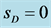 and
and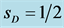 , respectively.
, respectively.
Figure 1, right plot. One can see that the discussed peak is sharp enough for both values of spin 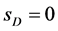 and
and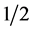 .
.
Characteristic values for singular points in the energy distributions of muons (kink and peak) together with similar points for the energy distributions of  (dijets) are given in Table1
(dijets) are given in Table1
The cascade 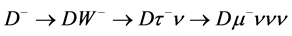 modifies the spectra just discussed. The energy distribution of
modifies the spectra just discussed. The energy distribution of  produced in the decay
produced in the decay  is the same as that for
is the same as that for 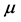 or
or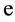 , discussed above (within the accuracy of
, discussed above (within the accuracy of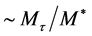 ). Once produced,
). Once produced, 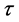 decays to
decays to 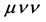 in 17% of cases (the same for decay to
in 17% of cases (the same for decay to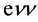 ). These muons are added to those discussed above.
). These muons are added to those discussed above.
In the 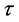 rest frame, the energy of muon is
rest frame, the energy of muon is 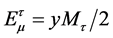 with
with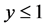 . The energy spectrum of muons is
. The energy spectrum of muons is  (see textbooks). This spectrum and the distributions obtained above are converted into the energy distribution of muons in the Lab frame. It is clear that this contribution is strongly shifted towards the soft end of the entire muon energy spectrum.
(see textbooks). This spectrum and the distributions obtained above are converted into the energy distribution of muons in the Lab frame. It is clear that this contribution is strongly shifted towards the soft end of the entire muon energy spectrum.
The resulting distribution retains the upper boundary of the energy distribution of muons 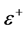 (12), (14). Numerical examples show that here the upper kink is smeared, while lower kink
(12), (14). Numerical examples show that here the upper kink is smeared, while lower kink  become even more sharp without shift from position (13) in wide region of masses
become even more sharp without shift from position (13) in wide region of masses  and
and . The position of peak (15) is also shifted weakly.
. The position of peak (15) is also shifted weakly.
2.4. Additional Decay Channels at 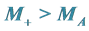
At  the decay
the decay 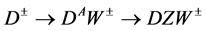 become possible and the processes
become possible and the processes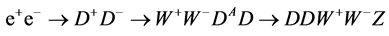 , etc. with signature (7) should be taken into account.
, etc. with signature (7) should be taken into account.
The total probability of 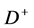 decay to
decay to  and
and 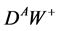 equals 1. The decay
equals 1. The decay 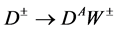 is described by the same equation as
is described by the same equation as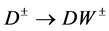 , but with other kinematical factors since
, but with other kinematical factors since . In the IDM the probability of this new decay is lower than that without
. In the IDM the probability of this new decay is lower than that without 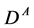 due to smaller final phase space, i.e.
due to smaller final phase space, i.e.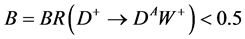 . In the MSSM value of
. In the MSSM value of 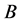 depends additionally on the mixing angles. We assume that in general case
depends additionally on the mixing angles. We assume that in general case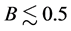 .
.
Below we limit ourself by the study of processes with signature (6b), (7a). Unfortunately, some of new processes with intermediate 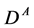 look as those with signature (6) since large fraction (20%) of decays of
look as those with signature (6) since large fraction (20%) of decays of  is invisible (
is invisible (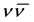 final states). We denote these states of
final states). We denote these states of 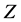 as
as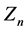 .
.
Let us consider in more detail production of an observed state with signature (6b), (7a) 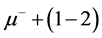 dijets
dijets  nothing. This state can be obtained from two different cascades.
nothing. This state can be obtained from two different cascades.
1) The cascade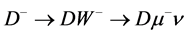 . The energy distribution of
. The energy distribution of  here reproduces
here reproduces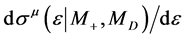 , discussed in Section 2.3 with an additional factor
, discussed in Section 2.3 with an additional factor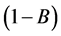 .
.
2) Cascade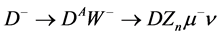 . Since couplings
. Since couplings 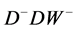 and
and 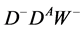 differ by a phase factor only (and perhaps mixing angle factors), the energy distribution of
differ by a phase factor only (and perhaps mixing angle factors), the energy distribution of 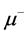 in this case is described by the same dependence
in this case is described by the same dependence 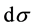 but with the change
but with the change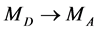 , the corresponding contribution to the entire energy distribution is
, the corresponding contribution to the entire energy distribution is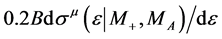 . For brevity we will write
. For brevity we will write 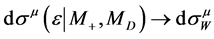 and
and
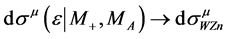 . The resulting energy distribution is
. The resulting energy distribution is
 (17)
(17)
The shape of the distribution  is similar to that for
is similar to that for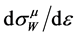 , but with different positions of kinks and (or) peak. As
, but with different positions of kinks and (or) peak. As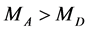 , these new kinks and (or) peak are situated below similar points for
, these new kinks and (or) peak are situated below similar points for . Since this contribution is much smaller than the main contribution
. Since this contribution is much smaller than the main contribution 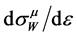 (with the overall ratio
(with the overall ratio 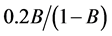 at
at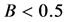 ), it only results in a weak reshaping of the full energy distribution as compared with distributions
), it only results in a weak reshaping of the full energy distribution as compared with distributions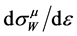 .
.
Note that in the case 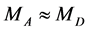 the distributions
the distributions 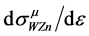 and
and 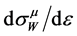 are close to each other, and
are close to each other, and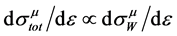 . In the opposite degenerate case
. In the opposite degenerate case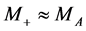 , the quantity
, the quantity 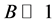 and the influence of the intermediate
and the influence of the intermediate 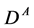 state on the result is negligible. (Such very cases are widely discussed in context of MSSM).
state on the result is negligible. (Such very cases are widely discussed in context of MSSM).
3. The Overall Picture
Observation of events with signature (6), (7) will be a clear signal for DM particle candidates. The nonobservation of such events will allow to find lower limits for masses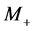 , like [11] -[13] . One can hope that these limits will be close to the beam energy
, like [11] -[13] . One can hope that these limits will be close to the beam energy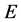 .
.
At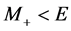 , the cross section
, the cross section 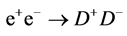 is a large fraction of the total cross section of
is a large fraction of the total cross section of 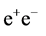 annihilation, and it makes this observation a very realistic task.
annihilation, and it makes this observation a very realistic task.
3.1. Distortion of the Obtained Results
A more detailed analysis reveals two sources of distortion of the obtained results (we neglect them in our preliminary analysis).
1. The final width of 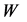 and
and 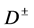 (
(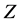 and
and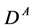 ) leads to a blurring singularities derived. This effect increases with the growth of
) leads to a blurring singularities derived. This effect increases with the growth of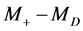 .
.
2. The energy spectra under discussion will be smoothed due to QED initial state radiation (ISR), final state radiation (FSR) and beamsstrahlung (BS). The ISR and FSR spectra are machine independent, while BS spectrum is specific for each machine (but well known during operations). This smoothing decreases accuracy in measuring of masses. However, the precise knowledge of mentioned spectra allows to solve the problem about restoration original accuracy by means methods of deconvolution in so called “incorrect inverse problem”. This work and the estimates of the range where masses and spins can be determined with reasonable accuracy will be the subject of the forthcoming paper.
3.2. Masses
Masses 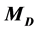 and
and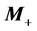 . In a well known approach, one measures edges in the energy distributions of dijets, representing
. In a well known approach, one measures edges in the energy distributions of dijets, representing 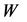 in the decay
in the decay 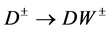 [5] [6] . However, the individual jet energies and consequently, effective masses of dijets cannot be measured with a high precision. The observed lower edge of the
[5] [6] . However, the individual jet energies and consequently, effective masses of dijets cannot be measured with a high precision. The observed lower edge of the 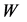 energy distribution in the dijet mode and the position of a peak in this distribution (11) are smeared by this uncertainty. One can only hope for a sufficiently accurate measurement of the upper edge of the
energy distribution in the dijet mode and the position of a peak in this distribution (11) are smeared by this uncertainty. One can only hope for a sufficiently accurate measurement of the upper edge of the 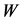 energy distribution,
energy distribution, 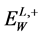 (9), (10).
(9), (10).
We suggest to extract the second quantity for description of masses from the lepton energy spectra. The lepton energy is measurable with a high accuracy. We found above that the singular points of the energy distribution of the leptons in the final state with signature (6a) are kinematically determined, and therefore can be used for a mass measurement.
M1) If a 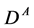 particle is absent or
particle is absent or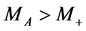 , the results (12)-(15) describe the energy distributions completely. The shape of the energy distribution of leptons (with one peak or two kinks) allows to determine which case is realized,
, the results (12)-(15) describe the energy distributions completely. The shape of the energy distribution of leptons (with one peak or two kinks) allows to determine which case is realized, 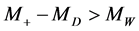 or
or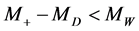 .
.
At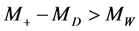 , the positions of upper edge in the dijet energy distribution
, the positions of upper edge in the dijet energy distribution 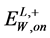 (9) and the lower kink in the muon energy distribution
(9) and the lower kink in the muon energy distribution 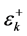 (13) give us two equation necessary for determination of
(13) give us two equation necessary for determination of 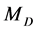 and
and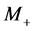 . We reproduce these equations for clarity
. We reproduce these equations for clarity
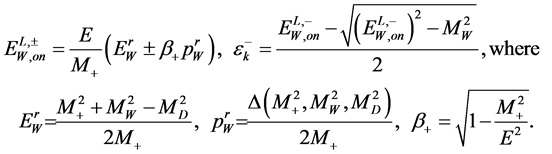 (18)
(18)
At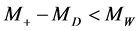 , two similar equations are provided by the position of the upper edge in the dijet energy distribution
, two similar equations are provided by the position of the upper edge in the dijet energy distribution 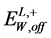 (10) and the peak in muon energy distribution
(10) and the peak in muon energy distribution  (15).
(15).
In both cases the position of the upper edge in the dijet energy distribution  or
or 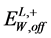 should be extracted from all events with signature (6), (7), the position of the lower kink in the muon energy distribution
should be extracted from all events with signature (6), (7), the position of the lower kink in the muon energy distribution  or peak
or peak 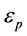 can be extracted from events with signature (6b) only.
can be extracted from events with signature (6b) only.
M2) The signal of realization of the inequality 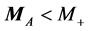 will be observation of the process
will be observation of the process , having signature (26). In this case the position of the upper edge in the dijet energy distribution is the same as in previous case. The position of lower edge in the dijet energy distribution is either shifted or smeared, in this case the method of [5] [6] becomes completely inapplicable. The entire energy distribution of muons in the observed state
, having signature (26). In this case the position of the upper edge in the dijet energy distribution is the same as in previous case. The position of lower edge in the dijet energy distribution is either shifted or smeared, in this case the method of [5] [6] becomes completely inapplicable. The entire energy distribution of muons in the observed state 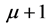 or
or 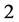 dijet
dijet 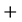 nothing was described in the Section 2.4. It was shown there that taking into account a new decay channel
nothing was described in the Section 2.4. It was shown there that taking into account a new decay channel 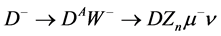 changes the position of the main singularities in the muon energy spectrum very weakly. Therefore the above mentioned procedure for finding
changes the position of the main singularities in the muon energy spectrum very weakly. Therefore the above mentioned procedure for finding 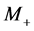 and
and 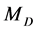 can be used in this case as well.
can be used in this case as well.
The opportunity to extract new singularities from the data, related to  (and giving additionally
(and giving additionally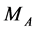 ), requires a separate study (see also analysis in Appendix B).
), requires a separate study (see also analysis in Appendix B).
3.3. Spin of 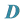 -Particles
-Particles 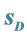
 The amplitude of the process
The amplitude of the process 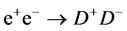 is the sum of model-independent QED diagram (the photon annihilation), the
is the sum of model-independent QED diagram (the photon annihilation), the  annihilation diagram and in some models
annihilation diagram and in some models  -channel exchange by other
-channel exchange by other 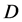 -odd particles. We start with the description of cross section in the minimal approximation, taking into account only photon and
-odd particles. We start with the description of cross section in the minimal approximation, taking into account only photon and 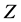 annihilation diagrams. Neglecting terms
annihilation diagrams. Neglecting terms 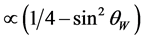 (described
(described  interference) we have:
interference) we have:
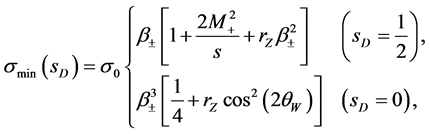 (19)
(19)
where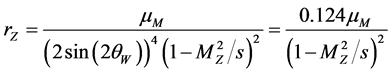 , factor
, factor 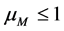 is expressed via parameters of possible mixing, etc. Figure 2 and Table 2 represent dependence of
is expressed via parameters of possible mixing, etc. Figure 2 and Table 2 represent dependence of 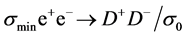 (19) on beam energy
(19) on beam energy 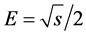 for
for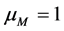 .
.
The cross section of the process is reduced by contribution of the diagram with  -channel exchange by other
-channel exchange by other 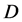 -odd particle
-odd particle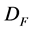 . This decrease is not so strong if mass of
. This decrease is not so strong if mass of 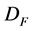 is high enough. For example, if mass of selectron is more than 250 GeV (condition 2 in Section 1 and [20] ), the cross section for
is high enough. For example, if mass of selectron is more than 250 GeV (condition 2 in Section 1 and [20] ), the cross section for 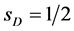 is reduced by a factor
is reduced by a factor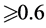 ,
,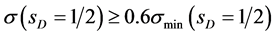 . Combining with numbers from Figure 2 and Table 2 we
. Combining with numbers from Figure 2 and Table 2 we
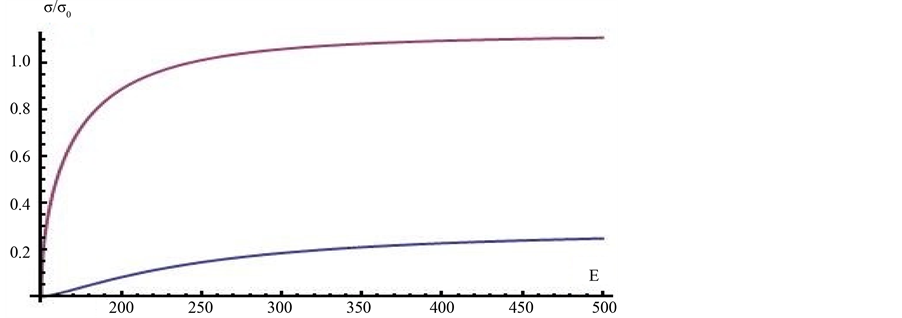
Figure 2. The upper curve for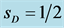 , the lower for
, the lower for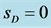 ;
; 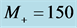 GeV.
GeV.
Table 2. Some values of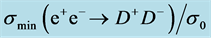 .
.
obtain (for identical masses  at a given beam energy
at a given beam energy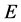 ):
):
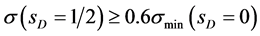 (20)
(20)
 The experimental value of the
The experimental value of the  cross section is obtained by summing over all processes with signature (6), (7) (that is about 3/4 of the total cross section). By taking into account the known BR’s for
cross section is obtained by summing over all processes with signature (6), (7) (that is about 3/4 of the total cross section). By taking into account the known BR’s for 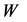 decay the accuracy of this restoration of
decay the accuracy of this restoration of 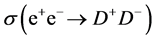 can be improved.
can be improved.
When masses 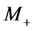 become known, the cross section
become known, the cross section 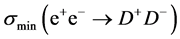 is calculated with reasonable precision with Equation (19). The strong inequality (20) allows to determine spin
is calculated with reasonable precision with Equation (19). The strong inequality (20) allows to determine spin 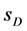 from the obtained values of cross sections even with a handful of well-reconstructed events.
from the obtained values of cross sections even with a handful of well-reconstructed events.
4. Conclusions
We consider models in which stability of dark matter particles 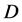 is ensured by conservation of new quantum number referred to as
is ensured by conservation of new quantum number referred to as 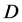 -parity. Besides these models contain charged particles
-parity. Besides these models contain charged particles  with the same
with the same 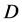 -parity. (Examples Inert Doublet Model with scalar
-parity. (Examples Inert Doublet Model with scalar 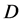 -particles and MSSM with
-particles and MSSM with 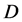 -particle of spin 1/2 and
-particle of spin 1/2 and  - parity equal
- parity equal 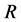 -parity). In these models we have studied the energy distribution of single lepton in the process like
-parity). In these models we have studied the energy distribution of single lepton in the process like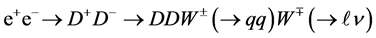 , having high enough cross section. Simple analysis allows us to establish that this distribution has singular points, kinks, peaks and end points, which are driven by kinematics only, and therefore are model-independent. Based on this analysis, we propose to use the mentioned distribution at future linear
, having high enough cross section. Simple analysis allows us to establish that this distribution has singular points, kinks, peaks and end points, which are driven by kinematics only, and therefore are model-independent. Based on this analysis, we propose to use the mentioned distribution at future linear  collider ILC, CLIC, etc. for precise measuring of masses of dark matter particles and charged particles
collider ILC, CLIC, etc. for precise measuring of masses of dark matter particles and charged particles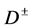 .
.
This method is in several aspects superior to the standard approaches discussed elsewhere.
1) It uses leptons which are copious and can be accurately measured in contrast with jets that individual energy can be measured only with lower precision.
2) These singularities are robust and survive even when superimposed on top of any smooth background.
In addition, even a rough measurement of cross sections with a very clean signature allows us to determine spin of DM particles based on the results of mentioned kinematical measurements.
Acknowledgments
This work was supported in part by grants RFBR and NSh-3802.2012.2, Program of Dept. of Phys. Sc. RAS and SB RAS “Studies of Higgs boson and exotic particles at LHC” and Polish Ministry of Science and Higher Education Grant N202 230337. I am thankful to A. Bondar, E. Boos, A. Gladyshev, A. Grozin, S. Eidelman, I. Ivanov, D. Ivanov, D. Kazakov, J. Kalinowski, K. Kanishev, P. Krachkov and V. Serbo for discussions.
References
- Hooper, D. (2009) TASI 2008 Lectures on Dark Matter. arXiv:0901.4090 [hep-ph]
- Maniatis, M. (2009) The Next-to-Minimal Supersymmetric extension of the Standard Mod. arXiv:0906.0777 [hep-ph]
- Kazakov, D.I. (2010) Supersymmetry on the Run: LHC and Dark Matter. arXiv:1010.5419 [hep-ph]
- Ellis, J. (2010) New Light on Dark Matter from the LHC. arXiv:1011.0077 [hep-ph]
- Li, Y. and Domerotski, A. (2010) Chargino and Neutralino Masses at ILC. arXiv: 1007.0698
- Asano, M., Fujii, K., Hundi, R.S., Itoh, H., Matsumoto, S., Okada, N., Saito, T., Suehara, T., Takubo, Y. and Yamamoto, H. (2011) Identification of new physics and general WIMP search at the ILC. arXiv:1007.2636 [hep-ph]
- Deshpande, N.G. and Ma, E. (1978) Physical Review D, 18, 2574-2576. http://dx.doi.org/10.1103/PhysRevD.18.2574
- Barbieri, R., Hall, L.J. and Rychkov, V.S. (2006) Improved Naturalness with a Heavy Higgs: An Alternative Road to LHC Physics. arXiv:hep-ph/0603188.
- Ginzburg, I.F., Kanishev, K.A., Krawczyk, M. and Sokolowska, D. (2010) Evolution of Universe to the present inert phase. arXiv:1009.4593 [hep-ph]
- Gustafsson, M., Rydbeck, S., Lopez-Honorez, L. and Lundstrom, E. (2012) Physical Review D, 86, Article ID: 075019. http://dx.doi.org/10.1103/PhysRevD.86.075019
- Espirito Santo, M., Hultqvist, K., Johansson, P. and Lipniacka, A. (2003) DELPHI 2003-002 PHYS 928. http://delphiwww.cern.ch/pubxx/delnote/dn2003.html
- Lundstrom, E., Gustafsson, M. and Edsjo, J. (2009) Inert Doublet Model and LEP II Limits. arXiv:0810.3924 [hep-ph]
- Aoki, M., Kanemura, S. and Yokoya, H. (2013) Reconstruction of Inert Doublet Scalars at the International Linear Collider. arXiv:1303.6191 [hep-ph]
- Dolle, E.M. and Su, S. (2009) Physical Review D, 80, Article ID: 055012. http://dx.doi.org/10.1103/PhysRevD.80.055012
- Dolle E., Miao X., Su S., Thomas B. (2010) Physical Review D, 81, Article ID: 035003.http://dx.doi.org/10.1103/PhysRevD.81.035003
- Lopez Honorez, L., Nezri, E., Oliver, J.F. and Tytgat, M.H.G. (2007) The Inert Doublet Model: An Archetype for Dark Matter. arXiv:0612275 [hep-ph]
- Nezri, E., Tytgat, M.Y.G. and Vertongen, G. (2009) Positrons and antiprotons from inert doublet model dark matter. arXiv:0901.2556 [hep-ph]
- Andreas, S., Hambye, T. and Tytgat, M.H.G. (2008) WIMP Dark Matter, Higgs Exchange and DAMA. arXiv: 0808.0255 [hep-ph]
- Honorez, L.L. and Yaguna, C.E. (2010) The Inert Doublet Model of Dark Matter Revisited. arXiv:1003.3125 [hep-ph]
- Particle Data Group (2012) Physical Review D, 86, Article ID: 010001. http://dx.doi.org/10.1103/PhysRevD.86.010001
- Heuer, R.D., et al. (2001) TESLA Technical Design Report, DESY 2001-011, TESLA Report 2001-23, TESLA FEL 2001-05.
- International Linear Collider TDR (2013) The International Linear Collider Technical Design Report—Volume 2: Physics. arXiv:1306.6352 [hep-ph]
- Moortgat-Pick, G. (2008) Journal of Physics: Conference Series, 110, Article ID: 072027. http://dx.doi.org/10.1088/1742-6596/110/7/072027
- Freitas, A., Martyn, H.U., Nauenberg, U. and Zerwas, P.M. (2004) Sleptons: Masses, Mixings, Couplings. arXiv: hepph/0409129
- Conley, J.A., Dreiner, H.K. and Wienemann, P. (2012) Measuring a Light Neutralino Mass at the ILC: Testing the MSSM Neutralino Cold Dark Matter Model. arXiv:1012.1035 [hep-ph]
- Ginzburg, I.F (2010) Simple and robust method for search Dark Matter particles and measuring their properties at ILC in various models of DM. arXiv:1010.5579 [hep-ph]
Appendix
A. Inert Doublet Model (IDM)
The IDM the 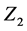 symmetric Two Higgs Doublet Model, containing two scalar doublets
symmetric Two Higgs Doublet Model, containing two scalar doublets 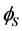 and
and , in which fermions are coupled to only field
, in which fermions are coupled to only field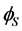 . The
. The 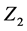 symmetry forbids
symmetry forbids 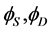 mixing. It is described by the Lagrangian
mixing. It is described by the Lagrangian
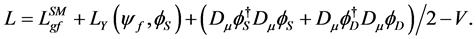 (21)
(21)
Here,  describes the
describes the 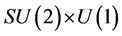 Standard Model interaction of gauge bosons and fermions. The
Standard Model interaction of gauge bosons and fermions. The 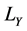 describes the Yukawa interaction of fermions
describes the Yukawa interaction of fermions 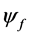 with only one scalar doublet
with only one scalar doublet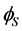 , having the same form as in the SM,
, having the same form as in the SM, 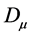 is standard covariant derivative,
is standard covariant derivative,
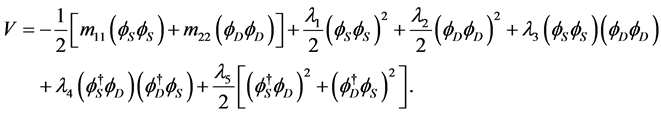 (22)
(22)
All parameters of this Higgs potential are real and condition of its stability has form
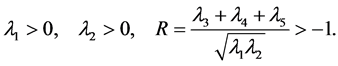 (23)
(23)
The IDM is realized at
 (24)
(24)
In this case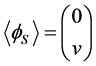 ,
, . Therefore, the doublet
. Therefore, the doublet 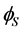 is responsible for electroweak symmetry breaking and the masses of fermions and gauge bosons just as in the Standard Model (SM). The second scalar doublet
is responsible for electroweak symmetry breaking and the masses of fermions and gauge bosons just as in the Standard Model (SM). The second scalar doublet  doesn’t receive vacuum expectation value and doesn’t couple to fermions.
doesn’t receive vacuum expectation value and doesn’t couple to fermions.
Four degrees of freedom of the Higgs doublet 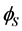 are such as in the SM: three Goldstone modes become longitudinal components of the EW gauge bosons, one component becomes the standard Higgs boson
are such as in the SM: three Goldstone modes become longitudinal components of the EW gauge bosons, one component becomes the standard Higgs boson . All the components of the scalar doublet
. All the components of the scalar doublet 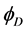 are realized as the massive
are realized as the massive 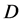 -particles: two charged
-particles: two charged  and two neutral ones
and two neutral ones ,
, 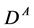 with masses
with masses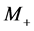 ,
, 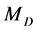 ,
,  respectively.
respectively.
 e By construction,
e By construction, 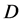 -particles possess a new conserved multiplicative quantum number (named here as
-particles possess a new conserved multiplicative quantum number (named here as 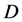 - parity) and therefore the lightest particle among them can be a candidate for DM particle. In this model all
- parity) and therefore the lightest particle among them can be a candidate for DM particle. In this model all 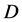 - particles have spin
- particles have spin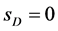 . The other features of IDM can be found in ref. [7] -[10] .
. The other features of IDM can be found in ref. [7] -[10] .
B. Process 
One more process leading to production of  -odd particles at ILC is also observable at
-odd particles at ILC is also observable at 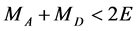 (in particular, at
(in particular, at  ):
):
 (25)
(25)
This process has a clear signature in the modes suitable for observation
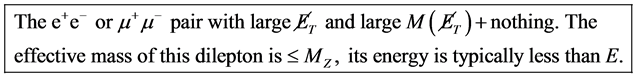 (26a)
(26a)
 (26b)
(26b)
At 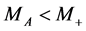 the BR for channel with signature (26a) is 0.06, for the channel with signature (26b) 0.7. We skip channel
the BR for channel with signature (26a) is 0.06, for the channel with signature (26b) 0.7. We skip channel  with
with 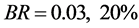 of decays of
of decays of 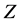 are invisible
are invisible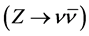 .
.
At 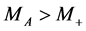 BR’s for processes with signature (26) become less, since new decay channels
BR’s for processes with signature (26) become less, since new decay channels 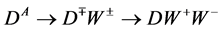 are added with signature
are added with signature
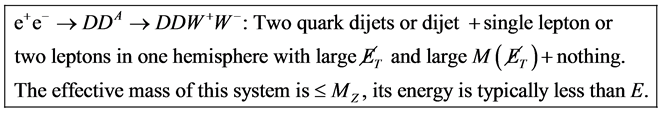 (27)
(27)
The cross section of the process 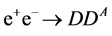 is model dependent. In the IDM it is determined unambiguously, in MSSM result depends on mixing angles and on the nature of fermions
is model dependent. In the IDM it is determined unambiguously, in MSSM result depends on mixing angles and on the nature of fermions  and
and  (Dirac or Majorana). In all considered cases at
(Dirac or Majorana). In all considered cases at 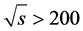 GeV this cross section is smaller than
GeV this cross section is smaller than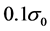 . Since the BR for events with signature (26a) is 0.06, at the luminosity (3) annual number of events with this signature is smaller than
. Since the BR for events with signature (26a) is 0.06, at the luminosity (3) annual number of events with this signature is smaller than . This number looks insufficient for kinematical analysis with high enough precision, (but limitations for masses can be obtained (cf. [11] -[13] for LEP)).
. This number looks insufficient for kinematical analysis with high enough precision, (but limitations for masses can be obtained (cf. [11] -[13] for LEP)).
Nevertheless we describe, for completeness, the energy distributions of  in this process. The obtained equations are similar to (4), (8)-(10) for new kinematics.
in this process. The obtained equations are similar to (4), (8)-(10) for new kinematics.
The 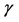 -factor and velocity of
-factor and velocity of 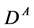 in c.m.s. for
in c.m.s. for 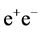 are
are
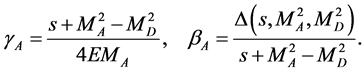 (28)
(28)
For production of 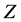 with an effective mass
with an effective mass 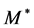 (
(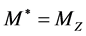 at
at 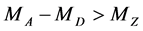 and
and 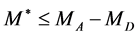 at
at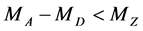 ) in the rest frame of
) in the rest frame of 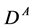
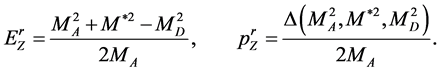 (29)
(29)
At 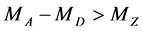 the
the 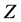 -boson energy
-boson energy 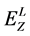 lies within the interval with edges
lies within the interval with edges
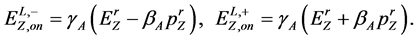 (30)
(30)
At 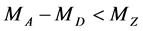 similar equations are valid for each value of
similar equations are valid for each value of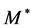 . Absolute upper and lower edges of the energy distribution of
. Absolute upper and lower edges of the energy distribution of  are reached at
are reached at :
:
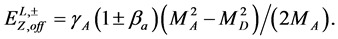 (31)
(31)
The peak in the energy distribution of dilepton appears at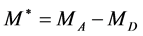 :
:
 (32)
(32)
Masses 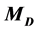 and
and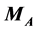 . At first sight, measurement of kinematical edges of the dilepton spectrum (30) (at
. At first sight, measurement of kinematical edges of the dilepton spectrum (30) (at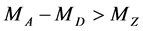 ) gives two equations for
) gives two equations for 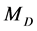 and
and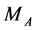 , allowing for determination of these masses. At
, allowing for determination of these masses. At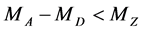 , the same procedure can be performed separately for each value of the effective mass of dilepton [26] . In the latter case, the absolute edges of the dilepton energy spectrum (31) and the position of the peak in this spectrum (32) could be also used for measuring
, the same procedure can be performed separately for each value of the effective mass of dilepton [26] . In the latter case, the absolute edges of the dilepton energy spectrum (31) and the position of the peak in this spectrum (32) could be also used for measuring 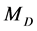 and
and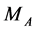 .
.
In any case, the upper edge in the dijet energy spectrum 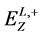 (30), (31) (signature (26)) gives one equation, necessary to find
(30), (31) (signature (26)) gives one equation, necessary to find 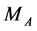 and
and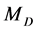 . In principle, necessary additional information gives position of lower edge in the dilepton energy spectrum
. In principle, necessary additional information gives position of lower edge in the dilepton energy spectrum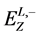 . However, as it was noted above, the anticipated number of events with signature (26a) looks insufficient for obtaining precise results. Together with good results for
. However, as it was noted above, the anticipated number of events with signature (26a) looks insufficient for obtaining precise results. Together with good results for 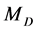 and
and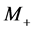 , one can hope to find an accurate value of
, one can hope to find an accurate value of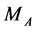 .
.
C. Backgrounds
C1. Background to the process with signature (6)
We show here that the cross sections of possible background processes (with suitable simple cuts) are 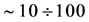 times less than the cross section of the signal process and therefore they can be neglected at analysis. Note that some our estimates can be corrected due to ISR and beamstrahlung.
times less than the cross section of the signal process and therefore they can be neglected at analysis. Note that some our estimates can be corrected due to ISR and beamstrahlung.
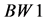 . The process
. The process 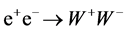 gives the same final state as those with signature (6). However, many of its features are not permitted by this signature. This fact allow to exclude the BW1 process from analysis with a good confidence applying suitable cuts.
gives the same final state as those with signature (6). However, many of its features are not permitted by this signature. This fact allow to exclude the BW1 process from analysis with a good confidence applying suitable cuts.
Let us discuss e.g. the observable mode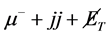 .
.
(a) For the process BW1 energy of each dijet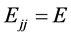 .
.
Application of cut in the dijet energy 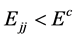 with large enough
with large enough 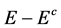 keeps all dijets from the signal process and leaves only small fraction of cross section of process BW1.
keeps all dijets from the signal process and leaves only small fraction of cross section of process BW1.
The dijet energy 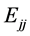 in BW1 can be less than
in BW1 can be less than 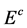 only if
only if 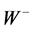 (seen as
(seen as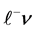 ) is strongly off shell with effective mass much higher than
) is strongly off shell with effective mass much higher than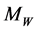 . The probability of such situation is estimated easily, it is
. The probability of such situation is estimated easily, it is 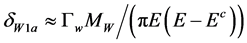 . The examples considered in the Table 1 allow to use cut
. The examples considered in the Table 1 allow to use cut 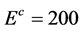 GeV and this cut leaves only 0.0012 of total cross section of BW1 process.
GeV and this cut leaves only 0.0012 of total cross section of BW1 process.
(b) For BW1 the missing mass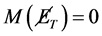 . Application of cut
. Application of cut 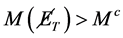 with suitable
with suitable 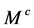 keeps all events of the signal process but diminishes contribution of BW1 in the events with signature (6A) even further.
keeps all events of the signal process but diminishes contribution of BW1 in the events with signature (6A) even further.
For dijet+dijet mode total energy of these dijets in the process BW1 differs from  only due to inaccuracy of measurements. For the examples considered in the Table 1 this energy deficit should be larger than 100 GeV.
only due to inaccuracy of measurements. For the examples considered in the Table 1 this energy deficit should be larger than 100 GeV.
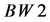 . The same (in its content) final state as we consider for signal process can be achieved via mechanism without at least one intermediate
. The same (in its content) final state as we consider for signal process can be achieved via mechanism without at least one intermediate 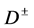 in
in 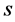 -channel, e.g.
-channel, e.g. . To simplify text of discussion, we will write here about the case
. To simplify text of discussion, we will write here about the case 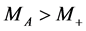 only.
only.
The contribution of this mechanism to the total cross section is at least in 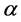 times less then that of the signal process. Indeed, in the signal process the value of cross section is given by the second order process
times less then that of the signal process. Indeed, in the signal process the value of cross section is given by the second order process . It includes the intermediate decay
. It includes the intermediate decay 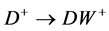 with probability 1, the corresponding cross section is
with probability 1, the corresponding cross section is 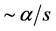 (an additional
(an additional  in the formal diagram is compensated by the small
in the formal diagram is compensated by the small 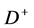 width
width 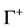 in the denominator of propagator). In the process BW2 we have third order process with decays in final stage (if
in the denominator of propagator). In the process BW2 we have third order process with decays in final stage (if 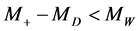 that is even the fourth order process). The neutrino exchange term enhances this contribution only logarithmically. If necessary, it can be reduced by variation of longitudinal polarization of initial electron and additionally by the cut in transverse momentum of muon
that is even the fourth order process). The neutrino exchange term enhances this contribution only logarithmically. If necessary, it can be reduced by variation of longitudinal polarization of initial electron and additionally by the cut in transverse momentum of muon 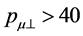 GeV.
GeV.
The interference of this BW2 mechanism with the signal one is also very small. In particular, in the signal process final leptons 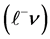 and
and 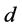 form system with effective mass
form system with effective mass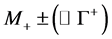 , while in the process BW2 this value of effective mass is only small part of entire phase space of this system, contributed to the total cross section.
, while in the process BW2 this value of effective mass is only small part of entire phase space of this system, contributed to the total cross section.
Therefore, the contribution of mechanism BW2 can be neglected with accuracy better than 1%.
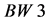 .
. . This background is absent if
. This background is absent if 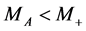 or
or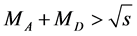 . If
. If 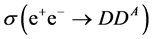 is not small at given
is not small at given , this fact will be seen via an observation of the process
, this fact will be seen via an observation of the process 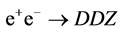 (26). The cross section
(26). The cross section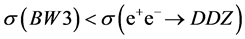 , i.e. it is much less than
, i.e. it is much less than 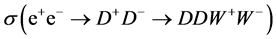 (roughly, by one order of magnitude). In this process all recorded particles move in one hemisphere in contrast to the with signal process, where they move in two opposite hemispheres. Therefore, the contribution of this background process may be reduced additionally by application of suitable cuts.
(roughly, by one order of magnitude). In this process all recorded particles move in one hemisphere in contrast to the with signal process, where they move in two opposite hemispheres. Therefore, the contribution of this background process may be reduced additionally by application of suitable cuts.
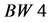 . In the SM processes with an observed state, satisfying criterion (6), large
. In the SM processes with an observed state, satisfying criterion (6), large 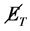 is carried away by additional neutrinos. The corresponding cross section is at least one electroweak coupling constant squared
is carried away by additional neutrinos. The corresponding cross section is at least one electroweak coupling constant squared 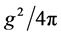 or
or  smaller than
smaller than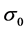 , with
, with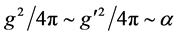 . Therefore,
. Therefore,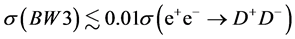 .
.
C2. Background to 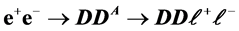
We consider these background processes only for completeness, since anticipated number of events for the process itself is not so large. We subdivide these background processes into 3 groups.
BZ1.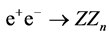 . At first sight, this process can mimic the process
. At first sight, this process can mimic the process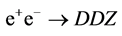 . However, the dilepton or dijet in this process have the same energy
. However, the dilepton or dijet in this process have the same energy 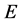 as the colliding electrons. The criterion (26) excludes such events from the analysis.
as the colliding electrons. The criterion (26) excludes such events from the analysis.
The cross section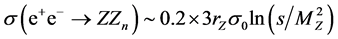 . The variants of this process with off-shell
. The variants of this process with off-shell , giving another effective mass of observed dijet or dilepton but with energy close to
, giving another effective mass of observed dijet or dilepton but with energy close to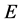 , has cross section which is smaller by a factor
, has cross section which is smaller by a factor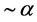 .
.
BZ2. Processes with independent production of separate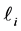 :
:
(BZ2.1)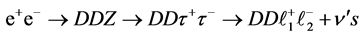 ,
,
(BZ2.2)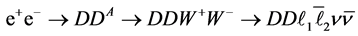 ,
,
(BZ2.3)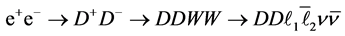 ,
,
(BZ2.4)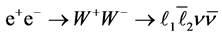 .
.
In these processes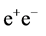 ,
,  ,
, 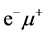 and
and 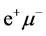 pairs are produced with identical probability and identical distributions. Hence, the subtraction from the
pairs are produced with identical probability and identical distributions. Hence, the subtraction from the  and
and 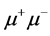 data the measured distributions of
data the measured distributions of 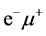 and
and 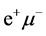 eliminates a contribution of these processes from the energy distributions under interest. This procedure does not implement substantial inaccuracies since cross sections of these processes after suitable cuts are small enough.
eliminates a contribution of these processes from the energy distributions under interest. This procedure does not implement substantial inaccuracies since cross sections of these processes after suitable cuts are small enough.
The cross sections of processes (BZ2.1), (BZ2.2) are small in comparison with that for . In the process (BZ2.3) leptons are flying in the opposite hemisphere, in contrast to the process under study
. In the process (BZ2.3) leptons are flying in the opposite hemisphere, in contrast to the process under study , where the leptons are flying in the same hemisphere. The cross section of the process (BZ2.4) is basically large. The application of cuts
, where the leptons are flying in the same hemisphere. The cross section of the process (BZ2.4) is basically large. The application of cuts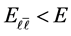 ,
, 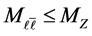 leaves less than
leaves less than 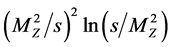 part of the cross section. The obtained quantity becomes smaller than that for the signal.
part of the cross section. The obtained quantity becomes smaller than that for the signal.
NOTES
![]()
1We use term “dijet” for all products of  decay in
decay in 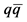 mode that are 2 quark jets or 2 quark jets plus gluon jet(s) or few hadrons for off shell
mode that are 2 quark jets or 2 quark jets plus gluon jet(s) or few hadrons for off shell  with small effective mass.
with small effective mass.
![]()
2We denote quantities in the rest system of 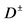 and in the Lab system by using superscripts
and in the Lab system by using superscripts 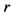 and
and  respectively, additional superscript
respectively, additional superscript 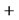 or
or  corresponds to upper or lower value of this quantity. Subscripts
corresponds to upper or lower value of this quantity. Subscripts 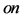 or
or 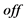 correspond to on shell or off shell
correspond to on shell or off shell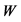 ’s, subscripts
’s, subscripts 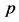 or
or 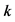 mark values, correspondent to peak or kink. Other subscripts and superscripts look evident.
mark values, correspondent to peak or kink. Other subscripts and superscripts look evident.
![]()
3We find useful, to mark in the argument of this distribution also masses of produced 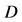 -particle
-particle 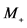 and
and 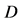 -particle appeared in its decay
-particle appeared in its decay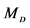 .
.



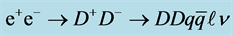 (in GeV) at
(in GeV) at 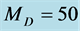 GeV.
GeV.