Journal of Modern Physics
Vol.5 No.3(2014), Article ID:43128,6 pages DOI:10.4236/jmp.2014.53020
IUPAC Periodic Table Quantum Mechanics Consistent
7, rue de l’Ambroisie 75012 Paris, France
Email: bschaeffer@wanadoo.fr
Copyright © 2014 Bernard Schaeffer. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Bernard Schaeffer. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 29, 2013; revised December 27, 2013; accepted January 25, 2014
Keywords:Periodic Table; Aufbau Principle; Exclusion Principle; Helium; Lutetium; Lawrencium; Quantum Mechanics
ABSTRACT
Most periodic tables of the chemical elements are between 96% and 100% in accord with quantum mechanics. Three elements only do not fit correctly into the official tables, in disagreement with the spherical harmonics and the Pauli exclusion principle. Helium, belonging to the s-block, should be placed beside hydrogen in the s-block instead of the p-block. Lutetium and lawrencium belonging to the d-block of the transition metals should not be in the f-block of the lanthanides or the actinoids. With these slight modifications, the IUPAC table becomes quantum mechanics consistent.
1. Introduction
The purpose of this paper is to find the necessary characteristics of a consistent periodic table of quantum mechanics, neglecting electron spin, “except that we adopt the exclusion principle” [1]. There is a great variety of periodic tables due to the various graphical, mathematical, physical or chemical criterions used. We shall modify slightly the official International Union of Pure and Applied Chemistry (IUPAC) table, in order to make it entirely compatible with the Schrödinger theory of the hydrogen atom. The Bohr Aufbau principle (lowest energy), Pauli exclusion principle (pairing), Hund’s rule (equal energy) and Madelung rule 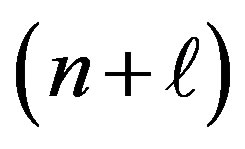 are briefly discussed.
are briefly discussed.
2. Short History of the Periodic Table
The Mendeleev table is more than one century old. It was originally based on atomic masses with twelve lines and eight columns, corresponding already but partially to the blocks s, p and d of quantum mechanics. The transition metals were moved separately and the rare gases replaced the corresponding column after their discovery by Ramsay. Moseley replaced the mass with the atomic number as a classification criterion. The transuranians were discovered by Seaborg who placed the lanthanoids and actinoids separately, below the table, for reasons of compactness. In 1985 the IUPAC Commission on the Nomenclature of Inorganic Chemistry proposed a new notation for the groups of the periodic table where the numbering of the groups was changed from VIII groups to 18 columns (Figure 1).
3. Description of the Periodic Table
The periodic table (Figure 1) has 4 blocks, the first one ( = 0), on the left, has two columns, one corresponds to the spin up and the second to the spin down with an exception, helium He, placed with the inert gases although it has 2 electrons instead of 6 in the next period (
= 0), on the left, has two columns, one corresponds to the spin up and the second to the spin down with an exception, helium He, placed with the inert gases although it has 2 electrons instead of 6 in the next period ( = 1). The fourth period (
= 1). The fourth period ( = 3) contains 10 columns with an anomaly on the first column, left. The last period (
= 3) contains 10 columns with an anomaly on the first column, left. The last period ( = 4) corresponding to the lanthanides and actinides, has 15 columns, an uneven number.
= 4) corresponding to the lanthanides and actinides, has 15 columns, an uneven number.
According to the Pauli exclusion principle of quantum mechanics, all elements are coupled: the elements with even atomic numbers have an even number of electrons and uneven elements have uneven numbers of electrons.
4. Periodic Table and Electronic Structure
The complete electronic structure of the atom (e.g. the hydrogen atom) is necessary to predict the physical and chemical properties of the elements. Some elements have configuration anomalies in the electronic sequence. For example chromium has the following electronic structure [Ar]4s13d5 and not the expected one, [Ar]4s23d4. This does not change the structure of the table because copper and chromium are in the middle of the d-block. Helium, lutetium and lawrencium, being at the boundary of their blocks, it is important to analyze their position.
4.1. Helium
It is well known that helium has a 1s2 structure, a spherical mode of vibration, as hydrogen 1s1; the difference resides in the number of electrons: two instead of one. Helium, pertaining to the s-block of the K-Shell (Figure 2), is usually placed with the other rare gases at the right of the table where the electronic structure of the outermost subshell is np6 with a maximum of six electrons instead of two for helium (1s2). Moreover, as Bartlett [2] has shown, the noble gases are not so inert. There exist compounds of xenon and krypton with fluorine, chlorine, hydrogen, platinum [3], gold [4]. There is no chemical reason any more to place helium with the other noble gases. Some authors put He in the p-block by writing the electronic structure as 1s2p0. p0 has no meaning: it contains no electron. The electronic structure of He is 1s2 and that’s all. The vacant box beside hydrogen waits for helium where it has its natural place.
He may be called a s-block noble gas. Its filled outer subshell s-block of valence electrons cannot appear in the p-block e.g. in column 18.
4.2. Lutetium and Lawrencium
Lutetium and lawrencium are traditionally considered to belong respectively to the lanthanoids and to the actinoids, with 15 elements each [3] instead of 14 in contradiction with the Pauli exclusion principle doubling the number of 7 spherical harmonics in the f-block. Indeed, each atom with an uneven atomic number is paired with the next atom, with an even atomic number. Lutetium (named Cassiopeium Cp by Bohr) has the structure (Xe)
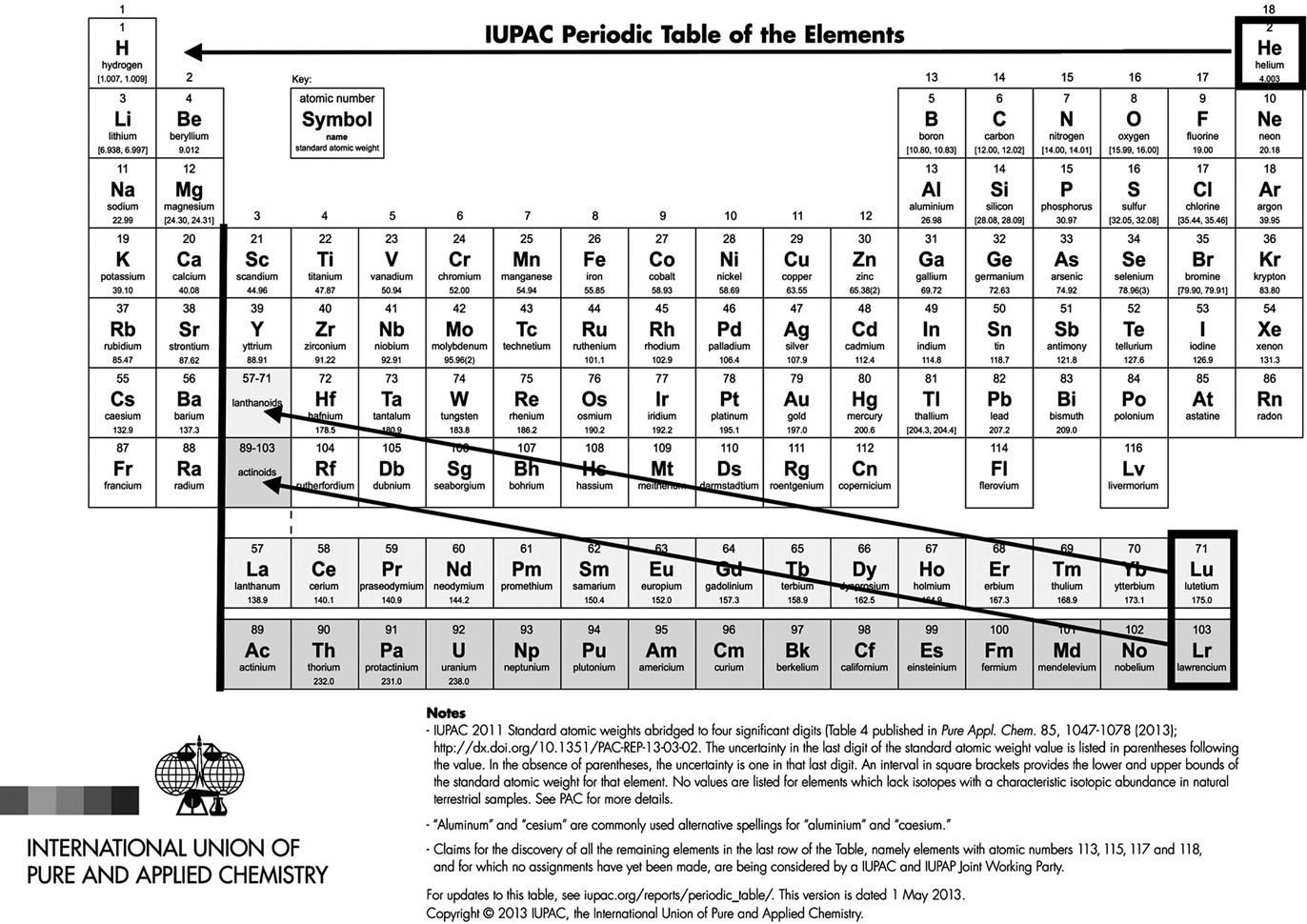
Figure 1. IUPAC official table, with suggested corrections. One can see a vacant place at the right of H, contradicting the heading “periodic table”: He should be there. According to quantum mechanics, the periods should be 2, 6, 10 and 14. The other anomaly is the lanthanides and actinides piled up into the Lu and Lr boxes! They should have an even number of elements each, e.g. 14 and not 15 and begin at the black vertical line. The two first columns should be to the right instead of the left but this is less important.

Figure 2. This corrected periodic table is built by applying the Schrödinger equation of quantum mechanics combined with the Pauli exclusion principle. The drawings show the plane nodes of the spherical harmonics (the spherical nodes do not show except for the fundamental orbital in dotted line). It is a slightly corrected IUPAC table where He is in the s-block instead of the p-block. Lutecium Lu and lawrencium Lr are in the d-block instead of the f-block: their correct location is shown bold on grey. All blocks have an even number of elements, paired in conformity with the Pauli exclusion principle. In order to have a regular increase of , from right to left, the two left columns,
, from right to left, the two left columns,  = 0, should be placed at the right of the table and one line higher in order to have the same n +
= 0, should be placed at the right of the table and one line higher in order to have the same n +  on a horizontal line, as in the Janet table.
on a horizontal line, as in the Janet table.
4f145d1s2, found by Bohr and Coster [5]. Having the first electron of the 5d subshell of the transition metals, it has to be in the d-block and not among the lanthanides, in the f-block.
With these changes, the Pauli exclusion principle is satisfied: the f-block, without Lu, contains an even maximum of 14 electrons. The two first rows of the d-block have each 10 elements; it should be the same for the two last rows. Indeed, lutetium and lawrencium pertain to the d-block of the transition metals with 10 elements and therefore not to the f-block of the lanthanoids. Lutetium and lawrencium may be called lanthanoid and actinoid of the d-block but cannot appear within the f-block with the 28 lanthanides and actinides. They have to be correctly placed below Sc and Y in the d-block as was shown by Bohr and co-workers [5]. After almost one century, this error has not yet been corrected. It is not because two persons resemble each other that they are of the same family.
5. Bohr Theory of the Hydrogen Atom
The Bohr theory of the hydrogen atom describes accurately the energy levels of the hydrogen atom and the Balmer series with circular trajectories of the electrons [5]. The electrons move around the nucleus like planets around the sun with a supplementary condition: the angular momentum should be quantized, that is an integer multiple of the reduced Planck constant h/2π, restricting the orbits to quantum integers.
6. Wave Mechanics of the Hydrogen Atom
Schrödinger developed a wave equation whose solutions are standing waves similar to the standing waves in a spherical resonator [6]. Born compares the hydrogen atom with a circular membrane fixed at the circumference. The number of radial nodal lines is the quantum number of the state of vibration [7]. The hydrogen nucleus with its electrostatic potential may be compared to a pond limited by a slope. The waves propagate at a variable velocity, like that of a tsunami function only of the water depth. The velocity of the matter waves [8] depends only on the velocity of the electron depending on the electrostatic potential, like a comet being captured by the sun if its velocity is smaller than the escape velocity. An electron approaching a proton will be captured in similar conditions. It loses energy by radiation until its angular momentum be exactly a multiple of the reduced Planck constant h. In the Schrödinger theory of the hydrogen atom, the electron emits permanently a stationary matter wave also called de Broglie wave [8]. The particle has to stay in the interference fringes of the matter wave with a probability proportional to the intensity of the wave, obtained by solving the Schrödinger equation. A stationary wave exists only for the Bohr values of the energy. The potential energy being function of the position r of the electron, the kinetic energy is the difference between the Bohr energy En of state n and the electrostatic potential V(r).
7. Related Empirical Principles
7.1. Bohr Aufbau Principle (1921)
The Aufbauprinzip (building-up principle) postulates a hypothetical process in which an atom is progressively “built up” from its predecessor, by adding one proton and one or more neutrons to the nucleus plus one electron to the outermost free atomic orbital [5]. The Aufbau is similar to building a house, following the blueprint. The periodic table is built from the top and increasing number of electrons from left to right.
7.2. Pauli Exclusion Principle (1925)
According to the Pauli exclusion principle, each orbital may contain one or two electrons only [9]. The electron has a magnetic moment like a tiny magnet due to its spinning electrical charge. Two opposite magnets attract themselves. A third electron is not attracted because the resulting magnetic moment of the magnets is zero. This means that the chemical elements are paired, an uneven atomic number is paired with the next one, having an even atomic number. They attract themselves when their magnetic moments are opposite, equilibrated by the centrifugal force.
7.3. Hund’s Rule (1925)
When electrons fill orbitals of equal energies, they occupy as many different orbitals as possible. Hund’s rule [10] may be interpreted as the reverse of the exclusion principle. Indeed, when the electrons are few, their distance on their orbit is large, the repulsive electrostatic force is thus stronger than the magnetic force. Hund’s rule is useful to predict the detailed electronic configuration but has no effect on the periodic table structure.
7.4. Madelung Rule (1926)
Also known after Janet (1927) the n +  rule [11] has been explained by Klechkowski (1962). Orbitals with a lower n +
rule [11] has been explained by Klechkowski (1962). Orbitals with a lower n +  value are filled before those with higher n +
value are filled before those with higher n +  values. In the case of equal n +
values. In the case of equal n +  values, the orbital with a lower n value is filled first. This is the quantitative formula corresponding to the Aufbau principle.
values, the orbital with a lower n value is filled first. This is the quantitative formula corresponding to the Aufbau principle.
8. Suggested Updating of the Compact Periodic Table
The periodic Figure 2, IUPAC style modified, is obtained from the spherical harmonics of Figure 3, combined with the Pauli exclusion principle. The drawings, modified from [12] show the spherical harmonics of the outermost orbitals of the atoms.
The vacant box beside hydrogen is now filled with helium. Lutetium and lawrencium are in the d-block below scandium and yttrium. The lanthanoids and actinoids are 14 each in the f-block as predicted by the exclusion principle and the spherical harmonics. As in most periodic tables, only the wave structure appears, not the real electronic structure of the atoms.
9. Conclusion
There exists a large variety of periodic tables, depending on the criterions used to build them. The chemical properties are not quantifiable, and their choice is as a criterion
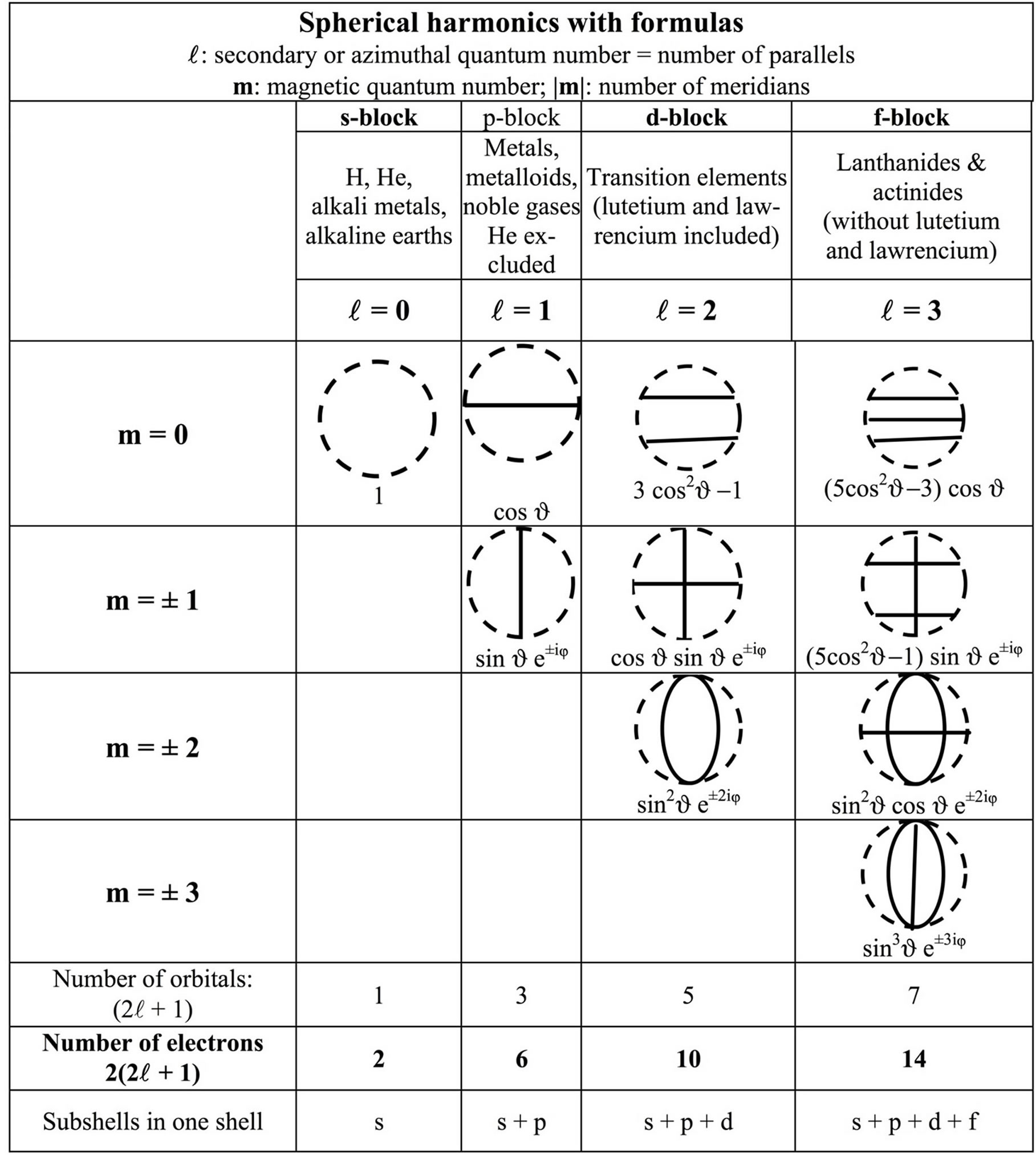
Figure 3. The void sphere (dotted circle) corresponds to the spherically symmetrical vibration mode of states with  = 0. It is the only spherical state represented by a dotted circle on Figure 2 for reason of visibility. All other modes have circular plane vibration nodes. The azimuthal quantum number
= 0. It is the only spherical state represented by a dotted circle on Figure 2 for reason of visibility. All other modes have circular plane vibration nodes. The azimuthal quantum number 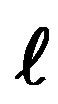 gives the number of parallels and the magnetic quantum number m, the number of meridians. The other spherical states are not shown on Figure 2 needing a more complicated table; if they were shown, they would appear as concentric circles [12].
gives the number of parallels and the magnetic quantum number m, the number of meridians. The other spherical states are not shown on Figure 2 needing a more complicated table; if they were shown, they would appear as concentric circles [12].
to build the periodic table being subjective. There are also purely mathematical arguments like symmetry criterions but their physical basis is tenuous. Most periodic tables being around 96% quantum mechanics consistent, 3 minor corrections are necessary. They consist to place hydrogen H, lutetium Lu and lawrencium Lr in their respective  -blocks. Helium will be therefore in the s-block side by side with hydrogen. Lutetium and lawrencium have to be moved from the f-block into the d-block, below yttrium Y. It may be acceptable to call He a noble gas of the s-block, Lu and Lr, lanthanide and actinide of the d-block. The IUPAC table with these three slight corrections would be practically entirely quantum mechanics consistent. An even better presentation would place the
-blocks. Helium will be therefore in the s-block side by side with hydrogen. Lutetium and lawrencium have to be moved from the f-block into the d-block, below yttrium Y. It may be acceptable to call He a noble gas of the s-block, Lu and Lr, lanthanide and actinide of the d-block. The IUPAC table with these three slight corrections would be practically entirely quantum mechanics consistent. An even better presentation would place the  = 0 elements to the right as in the Janet or left-step table [3,13].
= 0 elements to the right as in the Janet or left-step table [3,13].
REFERENCES
- R. P. Feynman, M. L. Sands and R. B. Leighton, “The Feynman Lectures on Physics, Quantum Mechanics,” California Institute of Technology, Pasadena, 1966.
- N. Bartlett, Proceedings of the Chemical Society, Vol. 6, 1962, p. 218.
- E. R. Scerri, “The Periodic Table: Its Story and Its Significance,” Oxford University Press, Oxford, 2006.
- A. K. Brisdon, Annual Reports on the Progress of Chemistry, Section A, Vol. 97, 2001, pp. 107-116. http://dx.doi.org/10.1039/b104213k
- N. Bohr, Nature, Vol. 112, 1923, pp. 29-44.
- E. Schrödinger, Annalen der Physik, Vol. 79, 1926, pp. 361-376. http://dx.doi.org/10.1002/andp.19263840404
- M. Born, “Atomic Physics,” Dover, New York, 1989.
- L. de Broglie, “Annales de Physique, 10e Série, Tome III,” Janvier-Février, 1925.
- W. Pauli, Zeitschrift für Physik, Vol. 31, 1925, pp. 373- 385. http://dx.doi.org/10.1007/BF02980592
- F. Hund, Zeitschrift für Physik, Vol. 33, 1925, pp. 345- 371. http://dx.doi.org/10.1007/BF01328319
- E. Madelung, “Mathematische Hilfsmtittel des Physikers,” 3rd Edition, Springer, Berlin,1936. http://dx.doi.org/10.1007/978-3-662-02177-4
- B. Schaeffer, “Relativités et Quanta Clarifiés,” Publibook, Paris, 2007.
- C. Janet, “Concordance de l’Arrangement Quantique, de Base, des Électrons Planétaires des Atomes—Avec la Classification Scalariforme, Hélicoïdale, des Éléments Chimiques,” Imprimerie Départementale de l’Oise, Beauvais, 1930.

