Journal of Modern Physics
Vol.5 No.1(2014), Article ID:42255,5 pages DOI:10.4236/jmp.2014.51005
Hubble Diagram Test of 280 Supernovae Redshift Data
Paul-Klee-Str.5, D-67061 Ludwigshafen am Rhein, Germany
Email: LaszloMarosi@aol.com
Received November 9, 2013; revised December 7, 2013; accepted January 2, 2014
ABSTRACT
We compare the Hubble diagram calculated from the observed redshift (RS)/magnitude (μ) data of 280 Supernovae in the RS range of z = 0.0104 to 8.1 with Hubble diagrams inferred on the basis of the exponential tired light and the Lambda Cold Dark Matter (ΛCDM) cosmological model. We show that the experimentally measured Hubble diagram follows clearly the exponential photon flight time (tS)/RS relation, whilst the data calculated on the basis of the ΛCDM model exhibit poor agreement with the observed data.
Keywords:Redshift/Magnitude Data Fitting; Linear Hubble Relation; Exponential Hubble Relation; ΛCDM Cosmological Model
1. Introduction
The basic assumption of the Lambda Cold Dark Matter (ΛCDM) cosmological model is that the universe is expanding, according to the Hubble’s law [1], at a velocity of v = zc = H0DC, where z is the redshift (RS), c is the velocity of light, H0 is the Hubble constant, and DC is the co-moving radial distance that can be derived from the observable z/μ data by (1).
 (1)
(1)
An important test of confidence in modeling the universal expansion is to compare the observed z/μ data with those derived on the basis of the ΛCDM model. The results presented in the literature, however, are not undisputed and are still a matter of debate. LaViolette [2] and more recently, López-Corredoira [3], Crawford [4], and Marosi [5-7] have shown that the static or slowly expanding universe models fit the observational data better than the data calculated on the basis of the presently prevailing ΛCDM model.
Such results, however, are usually refuted with the argument that the static universe contradicts many other cosmological observations, for example, the time dilation test and the cosmic microwave background (CMB) temperature versus RS test [8].
It is not the aim of this paper to argue in favor of or against either the expanding or static cosmological models. We only want to examine which of the two relations:
the linear Hubble’s law or the exponential 
fits the observational RS/μ data more accurately.
We mean that the result of a proper data fitting procedure of reliable observational data cannot be ignored out of respect to the predictions of a theory. If facts contradict the theoretical expectations, then the only scientifically adequate answer can be that the underlying theory is at best, incomplete.
In this paper, we analyze the observed Hubble diagram compiled from 280 supernovae z/μ data in the range of z = 0.0104 to 8.1. We expect that in the high RS range, it should be possible to check more precisely whether the Hubble diagram follows a linear z = H0DC/c relation, or the exponential
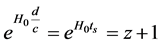 (2)
(2)
relation; an effect that is perceptible only slightly in the z < 1 region.
2. Data Collection and Processing
In our analysis, we have included 171 gold-set data [9], 59 calibrated high-RS gamma-ray burst (GRB) data (Hymnium data set) and 50 low-RS GRBs obtained by Wei [10] from the 557 Union 2-compilation.
As the z/μ data are plagued by considerable scatter, similar to the procedure described in [5], the potential μ = a × zb function was used to perform a global fitting over the RS range of z = 0.0104 to 8.1.
As differences between the different cosmological models become more pronounced only in the linear tS/z data representation, using Equations (2)-(4), the potential best fit data were converted into a tS/z data set.
The photon flight time tS was calculated from
 (3)
(3)
In Equations (2) and (3), tS means the flight time of the photons from the co-moving radial distance DC to the observer, which should not be confused with the photon travel time (t) in an expanding universe. tS means the flight time of photons between emission and reception, (tS = DC/c, c is the velocity of light), which is proportional to the DC that in entered in the linear Hubble law.
The photon flight time tS for the ΛCDM model was calculated with H0 = 72.6 km·s–1·Mpc–1, ΩM = 0.266, ΩΛ = 0.732 and k = 0 [11].
For the purpose of performing χ-squared tests in the high RS range of tS ×10–14 = 6000 to 11000 between the potential best fit and the tS/z data calculated on the basis of the ΛCDM model we included 41 equidistant tS/z data points in addition to the observed data.
The dimension of H0 for the exponential function is expressed by the energy loss with time and it has the dimension Hz·s–1·Hz–1 instead of km·s–1·Mpc–1 as in the ΛCDM model.
Excel, Excel Solver and WinSTAT [12] software were used for the data fitting, refinement, and analysis and data presentation.
3. Results
The potential best fit curve of the 280 observed z/μ data points is shown in Figure 1.
Four outliers with standard deviation > 3σ were identified in the z/μ data set and omitted from further regression analysis.
Results are shown in Tables 1 and 2.
It can be seen from Table 2 that the omitted outliers have relatively little influence on the regression coeffi-
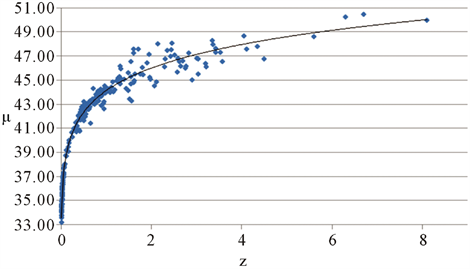
Figure 1. Solid line: potential μ = a × zb fit, diamonds: observed RS/μ data.
Table 2. Results of regression with μ = a × zb using 171, 276 and 280 z/μ data points.
cients a and b and that all the results for a and b lie within the very small error limits of a ± 0.02 and b ± 0.0006, respectively.
For further data treatment the potential best fit function obtained from 276 data points
 (4)
(4)
was used.
Tables 3-6 show the statistics of the fitting procedure with 276 data points.
4. The tS/(z + 1) Data Representation
Figure 2 shows the Hubble diagrams measured and calculated with 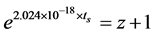 in the range of z + 1 = 1.0104 to 5.35.
in the range of z + 1 = 1.0104 to 5.35.
The goodness of fit indicators between the observed tS/(z + 1) data and the exponential e2.024x function for z + 1 = 1.0104 to 5.5, 6.5 and 9.1 are summarized in Table7 The precise agreement between the measured and calculated data in the range of z + 1 = 1.0104 to 5.5 strongly supports the conclusion that the tS/(z + 1) function is exponential. It seems very likely that the small deviations at z + 1 > 5.5 are due to small systematic errors in distance measurements or to the calibration method at very high RSs.
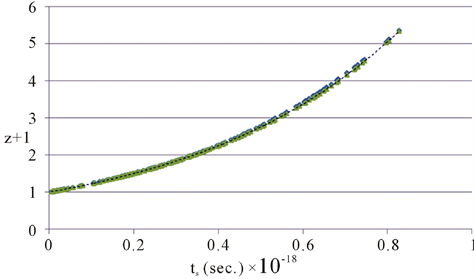
Figure 2. Observed data (diamonds), data calculated with  (triangles), trendline with e2.024x (dashed line).
(triangles), trendline with e2.024x (dashed line).
tS/z Diagram in the Range of z = 0.0104 - 8.1, Comparison with the ΛCDM Model
Figure 3 shows the tS/z diagram in the range of z = 0.0104 to 8.1 calculated using Equation (4) with the observed z/μ data set (squares), the exponential function  (triangles), and the tS/z relation derived from the ΛCDM model (circles) with H0 = 72.6 km s–1 Mpc–1, ΩM = 0.266, ΩΛ = 0.732 and k = 0.
(triangles), and the tS/z relation derived from the ΛCDM model (circles) with H0 = 72.6 km s–1 Mpc–1, ΩM = 0.266, ΩΛ = 0.732 and k = 0.
One can see from Figure 3 that, similar to the plot shown in Figure 2, the curves calculated from the best fit and the exponential function 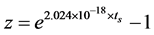 are nearly concurrent over the entire range of z, Pchi square = 1, whilst at z > 2 the tS/z data calculated based on the ΛCDM model show clearly a different slope and depart considerably from both, the linear and the exponential functions. The χ-square test indicates statistical significance between the observed tS/μ and the calculated ΛCDM data of P = 0.0173, indicating that from a statistical point of view, the two models are essentially different.
are nearly concurrent over the entire range of z, Pchi square = 1, whilst at z > 2 the tS/z data calculated based on the ΛCDM model show clearly a different slope and depart considerably from both, the linear and the exponential functions. The χ-square test indicates statistical significance between the observed tS/μ and the calculated ΛCDM data of P = 0.0173, indicating that from a statistical point of view, the two models are essentially different.
At RSs z < 0.3 (Figure 4), the tS/z curves for the potential best fit, the exponential function, and the ΛCDM model can be fitted with the linear function z = 0.000228725 × tS – 0.00332331 (R2 = 0.9989) with good approximation. The linear approximation, however, is deceiving. As can be seen in Figure 3, that at high RSs, the best-fit and the exponential curves follow strictly the exponential energy depletion relationship.
5. Conclusions
The most impressive result of the Hubble diagram test is
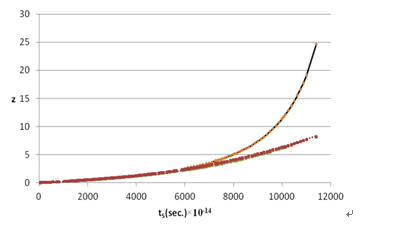
Figure 3. Redshift of type Ia supernovae as a function of tS = DC/c. Squares: tS/z data inferred from the potential best-fit curve of the observed z/μ diagram. Triangles: the exponential tS/z relation with H0 = 2.024 × 10–18. Circles: tS/z relation derived from the ΛCDM model with H0 = 72.6 km·s–1·Mpc–1.
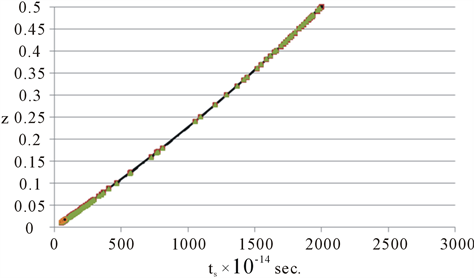
Figure 4. The “linear” tS/z relation in the low RS region for the potential best fit and the exponential function, and for the tS/z data calculated based on the ΛCDM model.
that the tS/z relation obtained from the potential best fit data can be expressed nearly exactly by the exponential formula 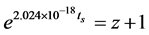 over the entire range of z = 0.01 to 8.1.
over the entire range of z = 0.01 to 8.1.
In contrast, in the RS range z > 2 the tS/z curve derived from the ΛCDM model with H0 = 72.6 km·s–1·Mpc–1, ΩM = 0.266, ΩΛ = 0.732 and k = 0, shows poor agreement with the observed data. The χ-square test indicates statistical significance between the observational potential fit and the calculated ΛCDM data of P = 0.0173, indicating that from a statistical point of view the two models are essentially different.
Based on the results presented in this paper, a reconsideration of the ΛCDM model appears warranted.
Acknowledgements
I am grateful to Professor Rainer Mattes of the Westfälische Wilhelms-Universität, Münster, Germany, for his support and his continuous interest in this work..
REFERENCES
- E. P. Hubble, Proceedings of the National Academy of Sciences of the United States of America, Vol. 15, 1929, pp. 167-173. Uhttp://dx.doi.org/10.1073/pnas.15.3.168U
- P. A. LaViolette, The Astrophysical Journal, Vol. 301, 1986, pp. 544-553. Uhttp://dx.doi.org/10.1086/163922U
- M. López-Corrediora, Recent Research in Development of Astronomy & Astrophysics, Vol. 1, 2003, p. 561. Uhttp://arxiv.org/abs/astro-ph/0310214U
- D. A. Crawford, The Journal of Cosmology, Vol. 13, 2011, pp. 3875-3946.
- L. A. Marosi, Advances in Astronomy, Vol. 2013, 2013, Article ID: 917104. Uhttp://dx.doi.org/10.1155/2013/917104U
- L. A. Marosi, “Hubble Diagram Test of Expanding and Static Cosmological Models, A New Interpretation of the Cosmic Redshift,” The General Science Journal, Research Papers-Astrophysics/Download/4931, 18 June 2013. http://gsjournal.net/Science-Journals/Essays-Astrophysics/Download/4931
- L. A. Marosi, Physics Research International, Vol. 2012, 2012, Article ID: 640605. Uhttp://dx.doi.org/10.1155/2012/640605U
- A. Sandage, “The Universe at Large. Key Issues in Astronomy and Cosmology,” Cambridge University Press, Cambridge, 1992.
- A. G. Riess, A. G. Sirolger, J. Tonry, et al., The Astrophysical Journal, Vol. 602, 2004, pp. 665-687. Uhttp://dx.doi.org/10.1086/383612U
- H. Wei, Journal of Cosmology and Astroparticle Physics, Vol. 2010, 2010, Article ID: 020. Uhttp://dx.doi.org/10.1088/1475-7516/2010/08/020U
- E. L. Wright, Publications of the Astronomical Society of the Pacific, Vol. 118, 2006, pp. 1711-1715. Uhttp://dx.doi.org/10.1086/510102U
- WinSTAT, “Statistik-Add-In für Microsoft® Excel,” R. Fitch Software, 2013. http://www.winstat.de


