Journal of Modern Physics
Vol.4 No.10(2013), Article ID:38868,5 pages DOI:10.4236/jmp.2013.410169
Gravity and Faster than Light Particles
1Isaac Newton Institute for Mathematical Sciences, Cambridge, UK
2Ariel University, Ariel, Israel
Email: asya@ariel.ac.il
Copyright © 2013 Asher Yahalom. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 16, 2013; revised July 18, 2013; accepted August 21, 2013
Keywords: general relativity; euclidian metric; superluminality
ABSTRACT
In this paper, I discuss whether superluminal particles exist in the general relativistic theory of gravity. It seems that the answer to this question is negative. In truth, the result may only represent a difficulty to special but not general relativity, the later allowing both Lorentzian and Euclidian metrics. An Euclidian metric does not restrict speed. Although only the Lorentzian metric is stable, an Euclidian metric can be created under special gravitational circumstances and persist in a limited region of space-time causing possible superluminality.
1. Introduction
It is well known that our daily space-time is approximately of Lorentz (Minkowski) type with a metric
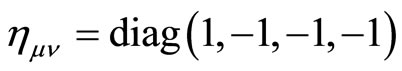 .
.
The above statement is taken as one of the central assumptions of the theory of special relativity and has been supported by numerous experiments. But one should ask why should it be so?
Many textbooks [1] state that in the general theory of relativity, any space-time is locally of the type
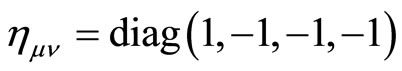 although it can not be presented so globally due to the effect of matter. This is a part of the demands dictated by the well known equivalence principle. The above principle is taken to be one of the assumptions of general relativity other assumption such as diffeomorphism invariance, and the requirement that theory reduce to Newtonian gravity in the proper regime lead to the Einstein equations:
although it can not be presented so globally due to the effect of matter. This is a part of the demands dictated by the well known equivalence principle. The above principle is taken to be one of the assumptions of general relativity other assumption such as diffeomorphism invariance, and the requirement that theory reduce to Newtonian gravity in the proper regime lead to the Einstein equations:
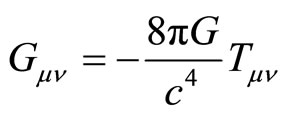 (1)
(1)
in which 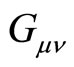 is the Einstein tensor,
is the Einstein tensor, 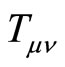 is the stressenergy tensor,
is the stressenergy tensor,  is the gravitational constant and
is the gravitational constant and 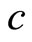 is the velocity of light.
is the velocity of light.
The Principle of Equivalence rests on the equality of gravitational and inertial mass, demonstrated by Galileo, Huygens, Newton, Bessel, and Eötvös. Einstein reflected that, as a consequence, no external static homogeneous gravitational field could be detected in a freely falling elevator, for the observers, their test bodies, and the elevator itself would respond to the field with the same acceleration [1]. This means that the observer will experience himself as free, not feeling the effect of any force at all. Mathematically speaking for the observer space time is locally (but not globally) flat and Minkowskian.
The point is that one need not assume that space-time is locally Lorentz based on an empirical (unexplained) facts, rather one can derive this property from the field equations based on the stability of the Minkowskian solution. Other unstable flat solutions of non Minkowskian type, such as an Euclidian metric  can exist in a limited region of space-time. In an Euclidian metric there are no speed limitations and thus the alleged particle can travel in faster than light speed. The reader should notice that already Eddington [2, Page 25] has considered the possibility that the universe contains different domains in which some domains are locally Lorentzian and others have some other local metric of the type
can exist in a limited region of space-time. In an Euclidian metric there are no speed limitations and thus the alleged particle can travel in faster than light speed. The reader should notice that already Eddington [2, Page 25] has considered the possibility that the universe contains different domains in which some domains are locally Lorentzian and others have some other local metric of the type

or the type
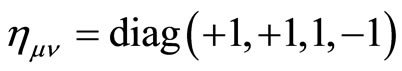 .
.
The stability of those domains was not discussed by Eddington.
Many authors have suggested explanations to the locally Lorentzian nature of space-time [3-6]. What is common to all the above approaches is that additional theoretical structures & assumptions are needed. In previous works [7-9] it was shown that General relativistic equations and linear stability analysis suffice to obtain a unique choice of the Lorentzian metric being the only one which is stable. Other metrics are allowed but are unstable and thus can exist in only a limited region of space-time. The analysis will not be repeated here, the reader is referred to the original literature. It should be mentioned that the choice of coordinates in the Fisher approach to physics is also justified using the stability approach [10]. The nonlinear stability question of the Lorentzian metric was settled by D. Christodoulou & S. Klainerman [11]. As for the nonlinear instability of other spaces of constant metric this remains an open question at this time.
The plan of this paper is as follows: in the first section we describe possible mechanisms of metric change. In the following section we describe a particle trajectory in a general flat space. The next section includes analysis of particle trajectories in Lorentz space-time for both the subluminal and superluminal cases. The following section will discuss dynamics in the presence of an Euclidean metric. Then the possible physical implications of the current theory are described. Finally some concluding remarks are given.
2. Possible Mechanisms of Metric Change
It was shown in [7] that among the possible flat space metrics only the Lorentzian metric is stable and can persist for a considerable region of space-time. Nevertheless one may still inquire if a mechanism exists by which a metric change does occur1, can we create some how a metric of the type

in some region of space-time? The answer obviously has to do with the only reason a metric should change according to equation (1) and this is . Looking at available solution of general relativity one finds that metric changes are quite common.
. Looking at available solution of general relativity one finds that metric changes are quite common.
The Schwarzschild square interval (in terms of spherical coordinates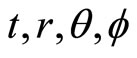 ) is given by:
) is given by:
 (2)
(2)
In which 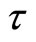 is the proper time, and
is the proper time, and 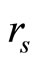 is the Schwarzschild radius (in meters) of the massive body, which is related to its mass
is the Schwarzschild radius (in meters) of the massive body, which is related to its mass  by
by
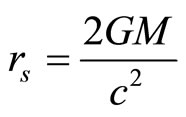 .
.
It is obvious that while for 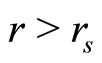 the metric is locally (up to scaling)
the metric is locally (up to scaling)
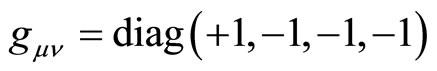 . For
. For 
the metric is locally (up to scaling)
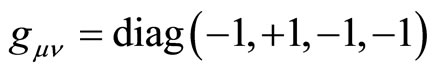 .
.
Hence the direction of temporal and (one) spatial axis is exchanged. Notice, however, that although the sign of the eigen-values did change we are still left with a Lorentzian metric.
Another example is the Friedman-LemaitreRobertson-Walker square interval which is well known in cosmological models:
 (3)
(3)
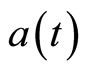 is known as the “scale factor” and
is known as the “scale factor” and 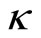 may be taken to have units of length
may be taken to have units of length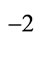 , in which case
, in which case  has units of length and
has units of length and 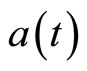 is unitless.
is unitless.  is then the Gaussian curvature of the space at the time when
is then the Gaussian curvature of the space at the time when . Hence for radial distances such that
. Hence for radial distances such that
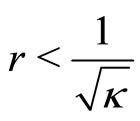
the metric is locally (up to scaling)
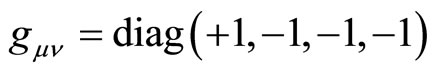
that is Lorentzian. However, for
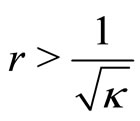
the metric is locally (up to scaling)
 .
.
this means that a particle propagating in a radial direction will experience an Euclidean metric.
One should notice that in the above cases a signature change is accompanied by a metric singularity [12] while the signature changes considered by Eddington [2] involve zeros. However, metric singularities are not curvature singularities and can be removed by proper choice of coordinates.
It will be also interesting to find a metric which is completely Euclidean in some regime of space-time, while being Lorentzian in another such a transitory metric may take the form
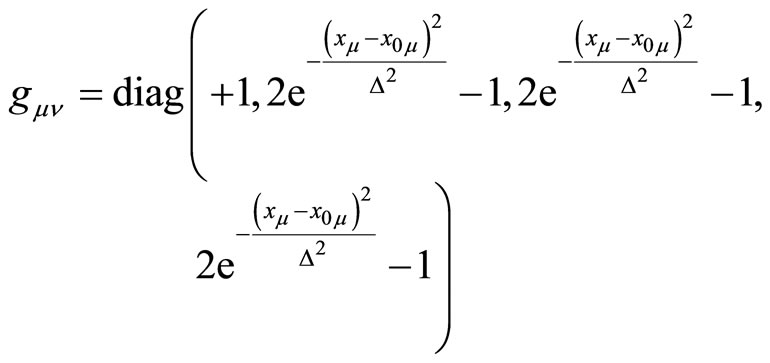
which is necessary to create an Euclidean domain of a width  located at
located at . More analytical effort should be invested in order to describe accurately the conditions under which space-time will become locally completely Euclidean.
. More analytical effort should be invested in order to describe accurately the conditions under which space-time will become locally completely Euclidean.
3. Particle Trajectories in Flat Space
Let us now look at a particle travelling in a space-time with a constant metric of arbitrary form. Such a particle can be described by the Action 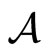 and Lagrangian
and Lagrangian :
:
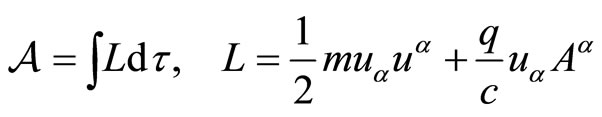 (4)
(4)
In the above  is some parameter along the trajectory,
is some parameter along the trajectory,  2 are the particle coordinates,
2 are the particle coordinates,
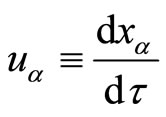 ,
,
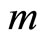 is the particle mass,
is the particle mass, 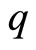 is the particle charge and
is the particle charge and 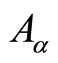 are some functions of the particle coordinates (that transform as a four dimensional vector). Basic variational analysis leads to the following equations of motion:
are some functions of the particle coordinates (that transform as a four dimensional vector). Basic variational analysis leads to the following equations of motion:
 (5)
(5)
It is customary to use as a parameter the length of the trajectory:
 (6)
(6)
in which 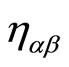 is the metric.
is the metric.
3.1. Lorentz Space-Time
Let us assume a Lorentz Space-Time with a metric
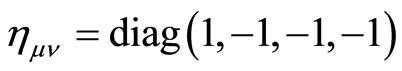 .
.
Hence space-time is dissected into spatial and temporal coordinates. The spatial coordinates are
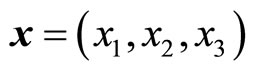
and the temporal coordinate is . Since it is customary to measure time in different units (seconds) than space (meters) we write
. Since it is customary to measure time in different units (seconds) than space (meters) we write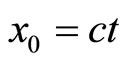 , in which
, in which 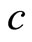 serves as a units conversion factor. We now define the velocity:
serves as a units conversion factor. We now define the velocity:
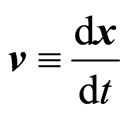 .
.
In a similar way we dissect 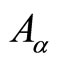 into temporal and spatial parts:
into temporal and spatial parts:
 (7)
(7)
Using equation (7) , we can define a magnetic field:
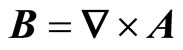 (8)
(8)
( has the standard definition of vector analysis) and an electric field:
has the standard definition of vector analysis) and an electric field:
 (9)
(9)
For subluminal particles  we can than write
we can than write 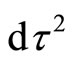 as:
as:
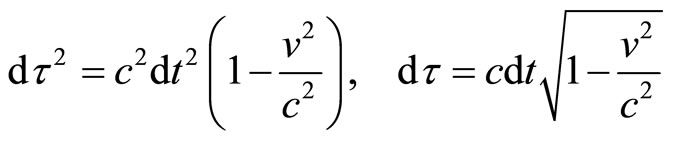 (10)
(10)
And using the above equations one can write the spatial part of equation (5) as:
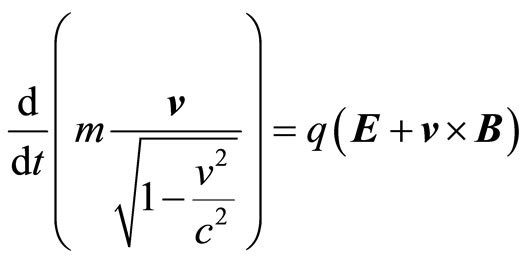 (11)
(11)
The above equation shows clearly that a subluminal particle in a Lorentz space must remain subluminal. Since as the particle is accelerated to 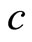 its “effective mass”
its “effective mass”
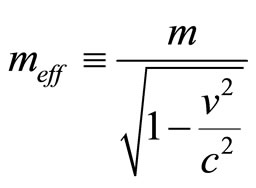
becomes infinite. On the other hand for superluminal particles (which are  at
at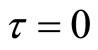 ) we can write
) we can write 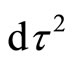 as:
as:
 (12)
(12)
And using the above equations one can write the spatial part of equation (5) as:
 (13)
(13)
Here the difficulty would be to go below the velocity 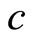 (invalidating claims that the particle losses energy by interacting with the gauge field and becomes subluminal again). In the absence of forces the velocity of the above particle remains constant and superluminal. We conclude that in a Lorentz space time there is a difficulty to pass the velocity
(invalidating claims that the particle losses energy by interacting with the gauge field and becomes subluminal again). In the absence of forces the velocity of the above particle remains constant and superluminal. We conclude that in a Lorentz space time there is a difficulty to pass the velocity  from below or above as is well known.
from below or above as is well known.
3.2. Euclidean Space-Time
Let us assume an Euclidean space-time with a metric
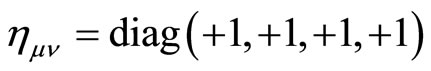 .
.
Here space-time is dissected (arbitrarily) into spatial and temporal coordinates as in the Lorentz space which are measured in the customary units. Again we define the velocity:

and dissect  into temporal and spatial parts as in equation (7). Using equation (7), we can define the magnetic field as in equation (8) but the electric field is defined now as:
into temporal and spatial parts as in equation (7). Using equation (7), we can define the magnetic field as in equation (8) but the electric field is defined now as:
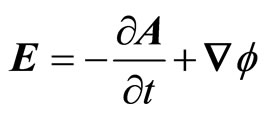 (14)
(14)
notice that this definition for the electric field is different than in the Lorentz space but is necessary in order to maintain Faraday’s law. For all particles either (subluminal or superluminal) we can than write  as:
as:
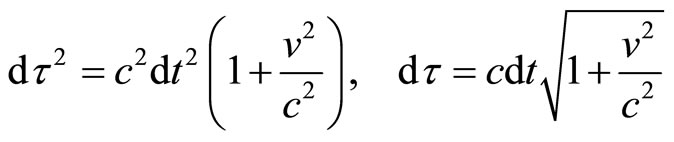 (15)
(15)
And using the above equations one can write the spatial part of equation (5) as:
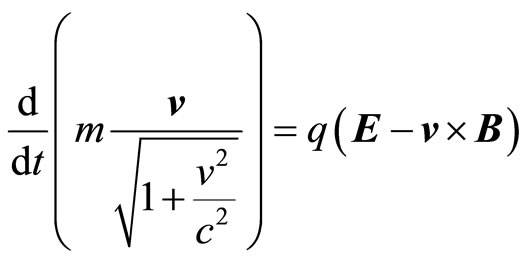 (16)
(16)
The above equation shows clearly that particles in an Euclidean space are quite indifferent to passing the velocity .
.
4. Some Possible Physical Implications
One obvious physical implication of the previous analysis is that a particle can be accelerated to a velocity close to the velocity 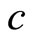 in a Lorentz space, enter into an Euclidean space and be accelerated further in this region to velocities above the speed
in a Lorentz space, enter into an Euclidean space and be accelerated further in this region to velocities above the speed 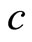 and emerge in a Lorentz space in which it will remain above the speed
and emerge in a Lorentz space in which it will remain above the speed 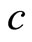 for ever unless it is decelerated in an Euclidean space again.
for ever unless it is decelerated in an Euclidean space again.
This certainly may happen to a particle which travels radially in a Friedman-Lemaitre-Robertson-Walker metric passing outwards the critical radius of
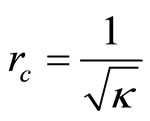
and then coming back at superluminal velocities.
But if such particles do exist how would their existence bear on existing physical and astrophysical problems?
An obvious implication has to do with the homogeneity problem, superluminal particle are not restricted by the velocity of light and hence can bring a very young universe into thermal equilibrium. Of course a more popular mechanism for achieving this is inflation [13]. However, one should notice that a Higgs type fields do not give the correct density perturbation spectrum [13], hence one is forced to postulate a new field which is not a part of any particle model and thus is a possible but inelegant solution of the homogeneity problem. Alternatively one can speculate that homogeneity is achieved by ordinary matter which can become superluminal as the current analysis shows.
Another implication which is less obvious is that superluminal particle consist of at least some part of galactic or inter-galactic dark matter [14] (26.8% of the matter in the universe are known to be dark). Since a quantum theory of superluminal particles is not well developed at this stage, such a theory once elaborated may suggest that those particles do not interact efficiently with radiation and thus appear dark.
A further implication has to do with the accelerating cosmological expansion. Since space-time has a different metric for 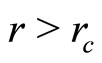 it may be that physics is different for such extreme distances. This bears on the correct interpretation of red shifts in such extreme distances as well.
it may be that physics is different for such extreme distances. This bears on the correct interpretation of red shifts in such extreme distances as well.
Last but not least one should remember that although classical physics is assumed to take place in a Lorentzian background, quantum field theory calculations are done in an Euclidean background using the Wick rotation. This is usually justified on the basis that it is an analytic continuation. But an analytic continuation is a mathematical technique which has no physical justification in Lorentzian space-time but makes perfect sense if part of space-time, in particular the part which is very close to the particle is Euclidean. Hence one may speculate that each elementary particle may carry with it a "bubble" of a microscopic Euclidean space-time.
5. Conclusion
We have shown that general relativity allows for nonLorentzian space-times, in particular this is allowed in part of the Friedman-Lemaitre-Robertson-Walker universe. The result of which is that superluminal particles can exist in such a cosmology. Some of the cosmological implications of superluminal particles regarding the homogeneity problem, and dark matter problems are underlined. Some other possible implications of non Lorentzian metrics which are not connected to superluminality but may be a consequence of non-Euclidean metrics are also suggested. Of course much more detailed analysis is needed to reach a definite conclusion regarding any of the above physical problems, but the existence of nonLorentzian space-times and superluminal particles suggests a plausible solution.
REFERENCES
- S. Weinberg, “Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity,” John Wiley & Sons, Inc., Hoboken, 1972.
- A. S. Eddington, “The Mathematical Theory of Relativity,” Cambridge University Press, Cambridge, 1923.
- A. Carlini and J. Greensite, Physical Review D, Vol. 49, 1994, pp. 866-878. http://dx.doi.org/10.1103/PhysRevD.49.866
- E. Elizalde, S. D. Odintsov and A. Romeo, Classical and Quantum Gravity, Vol. 11, 1994, p. L61-L68. http://dx.doi.org/10.1088/0264-9381/11/4/002
- Y. Itin and F. W. Hehl, Los Alamos Archive gr-qc/ 0401016, 2004.
- H. van Dam and Y. J. Ng, Los Alamos Archive hep-th/ 0108067, 2001.
- A. Yahalom, Foundations of Physics, Vol. 38, 2008, pp. 489-497. http://dx.doi.org/10.1007/s10701-008-9215-3
- A. Yahalom, International Journal of Modern Physics D, Vol. 18, 2009, pp. 2155-2158. http://dx.doi.org/10.1142/S0218271809016090
- A. Yahalom “Advances in Classical Field Theory,” Chapter 6, Bentham eBooks eISBN: 978-1-60805-195-3, 2011.
- A. Yahalom, International Journal of Modern Physics D, Vol. 19, 2010, pp. 1-5. http://dx.doi.org/10.1142/S0218271810018347
- D. Christodoulou and S. Klainerman, “The Global Nonlinear Stability of the Minkowski Space,” Seminaire Equations Aux Derivees Partielles (dit “Goulaouic-Schwartz,”), Princeton University Press, Princeton, 1989-1990, Exp. No. 13, p. 29.
- D. Lynden-Bell Private Communication.
- A. H. Guth, “Starting the Universe: The Big Bang and Cosmic Inflation,” In: J. Cornell, Ed., Bubbles, Voids and Bumps in Time: The New Cosmology, Cambridge University Press, Cambridge, 1995, p. 105
- V. C. Rubin, “Weighting the Universe: Dark Matter and Missing Mass,” In: J. Cornell, Ed., Bubbles, Voids and Bumps in Time: The New Cosmology, Cambridge University Press, Cambridge, 1995, p. 73.
NOTES
1In the sense that the eigen-values of the metric change signs.
2Raising and lowering indices is done using the metric as is customary.

