Journal of Modern Physics
Vol.4 No.9(2013), Article ID:36565,5 pages DOI:10.4236/jmp.2013.49159
Theory of Deuteron and MCPE
Department of Physics, Osmania University, Hyderabad, India
Email: cvavbc@gmail.com
Copyright © 2013 Chintalapati vavb Chandraraju. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 8, 2013; revised June 19, 2013; accepted July 4, 2013
Keywords: Morphed Potential Energy; Bindingenergy; Radius; Quadrupole Moment; Superposed State; Morphed Coulomb Potential Energy
ABSTRACT
All the experimental values of the Deuteron nucleus except the magnetic moment are theoretically derived using the ordinary methods of quantum mechanics along with the morphed gravitational potential energy. To convince that the potential energy function used is indeed the right one, it is applied to determine the energy spectrums of the nuclei: 1) Triton, 2) helium-3, 3) lithium-7, 4) Beryllium-9, and 5) Beryllium-8. The Morphed Coulomb Potential Energy (MCPE) is also obtained. With the help of MCPE and the gravitational potential energy of the electron, the charge quantum number is obtained. For galaxies, the two dominant forces that are responsible for the expansion, contraction or stationary state of the universe are obtained.
1. Introduction
The Deuteron nucleus is the simplest of all the nuclei. It consists of a Proton and a neutron with a total spin quantum number of one. The orbital angular momentum is zero. The binding energy of this nucleus is 2.2251 MeV. The Deuteron has a root-mean-square electro-magnetic radius of approximately 2.1 F [1]. A radio-frequency molecular beam method has been employed to determine the quadrupole moment of the Deuteron as Q = 0.00282 barn. The magnetic dipole moment is nuclear mag.
nuclear mag.
The Deuteron is a quantum mechanical system. Can we derive these results by the methods of quantum mechanics? To determine these results theoretically, one should know the correct potential energy that operates among the nucleons. In references [2,3], we obtained a potential energy which was closely connected to the gravitational potential energy. We called this potential energy the “Morphed Gravitational Potential Energy, MGPE”.
In Section 2, we will apply this MGPE for the Deuteron nucleus to find its energy spectrum and wave functions. In this section, we will determine the ground state energy as well as the radius of this nucleus. In Section 3 the quadrupole moment is estimated using the methods of quantum mechanics. The magnetic moment is also estimated in this section. Section 4 is used to determine the ground state wave functions and binding energies of some nuclei. Section 5 contains our conclusions.
2. Deuteron Nucleus
The morphed gravitational potential energy for the Deuteron nucleus is found to be [2,3]
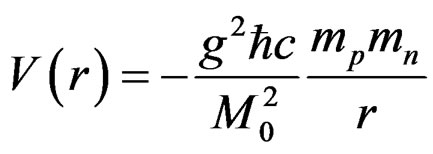 , (2.1)
, (2.1)
where,
 . (2.2)
. (2.2)
In the above expression 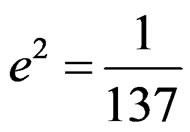 is the fine structure constant and 0.2254 is the Weinberg mixing parameter [4]. The parameter
is the fine structure constant and 0.2254 is the Weinberg mixing parameter [4]. The parameter  is different for each nucleus. For the Deuteron nucleus it is given by [3],
is different for each nucleus. For the Deuteron nucleus it is given by [3],
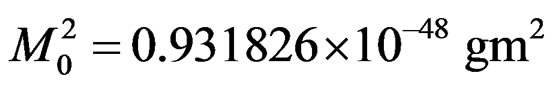 . (2.3)
. (2.3)
The time independent Schrödinger equation for the deuteron is given by,
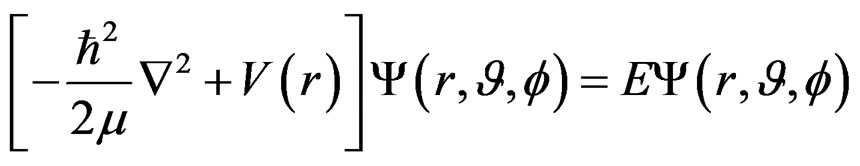 . (2.4)
. (2.4)
Here the reduced mass 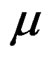 is given by,
is given by,
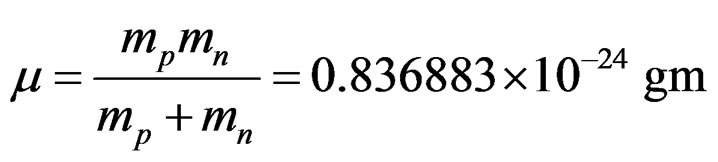 . (2.5)
. (2.5)
The spherically symmetric potential leads to the solution [5-7],
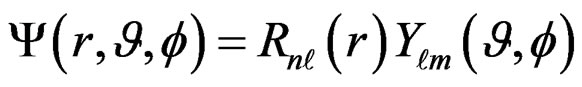 , (2.6)
, (2.6)
Where the quantum numbers n, 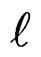 and m have the following values as in the case of the hydrogen atom:
and m have the following values as in the case of the hydrogen atom:
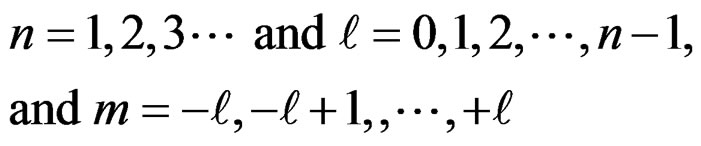
The radial wave function is given by,
 . (2.7)
. (2.7)
The dimensionless parameter  in Equation (2.7) is given by,
in Equation (2.7) is given by,
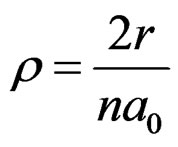 , where n is the principal quantum number. (2.8)
, where n is the principal quantum number. (2.8)
Here,
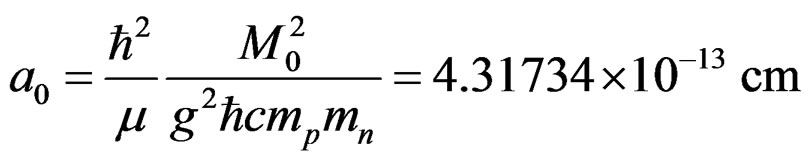 . (2.9)
. (2.9)
The energy spectrum for this case is given by,
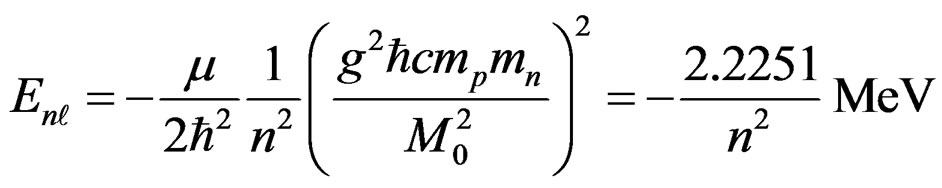 . (2.10)
. (2.10)
The normalization constant A in Equation (2.7) is given by,
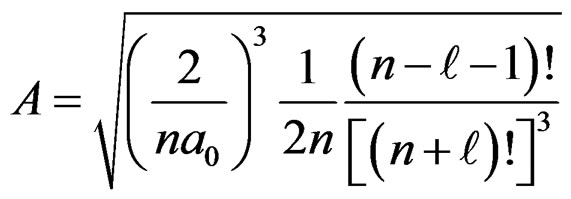 . (2.11)
. (2.11)
All the above results are obtained by a simple transcription of the hydrogen atom results with an appropriate change of variable. The ground state energy of the deuteron nucleus is given by −2.2251 Mev. This is an excellent result. The radius of the deuteron nucleus is half of Equation (2.9) whereas Equation (2.9) gives the distance between the two nucleons. The radius is the distance of either of the nucleons from the center of mass. This result also agrees pretty well with the experiment. There are excited energy levels but these are a blessing in disguise. These will be necessary to explain the quadrupole moment of the deuteron nucleus as we show in the next section.
3. The Quadrupole Moment and the Magnetic Moment of the Deuteron
Experimentally a small positive electric quadrupole moment is observed for the Deuteron. The total angular momentum quantum number J = 1 for the Deuteron. It is also in a definite state of parity. The J value equal to one can be obtained from different combinations of the orbital angular momentum 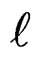 and the spin S such as,
and the spin S such as,
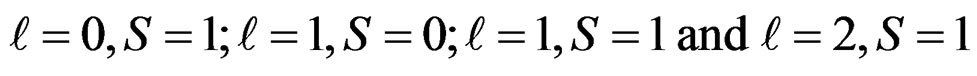 , (3.1)
, (3.1)
and no more. For the deuteron the principal element of the total wave function is the 3S1 state. The only other state in which the two particles give the same total angular momentum and parity is the 3D1 state (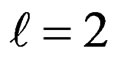 , S = 1 and J = 1). We therefore conclude that the total wave function of the deuteron must have the form
, S = 1 and J = 1). We therefore conclude that the total wave function of the deuteron must have the form
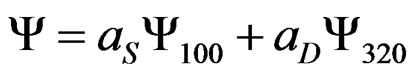 . (3.2)
. (3.2)
From Equations (2.6 & 2.7) we readily find that,
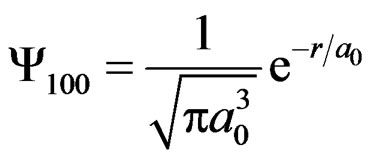 , (3.3)
, (3.3)
And,
 . (3.4)
. (3.4)
These wave functions are solutions of the Schrödinger equation of the deuteron nucleus with the morphed gravitational potential energy. The superposed state given by Equation (3.2) shows that the shape is not spherical and this leads to a quadrupole moment for the Deuteron nucleus. The quadrupole Moment is given by [8-10],
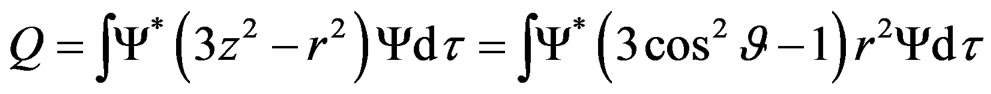 . (3.5)
. (3.5)
In the center of mass system the distance of the neutron and proton from the center of mass is r/2 and only the proton contributes to Q, the neutron being uncharged. The quadrupole moment is therefore given by,
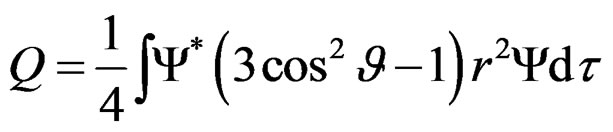 . (3.6)
. (3.6)
When we insert Equations (3.2)-(3.4) into Equation (3.6) we obtain four volume integrals and the very first integral will be zero, the second and third integrals are equal and the fourth integral is non-zero and this gives,
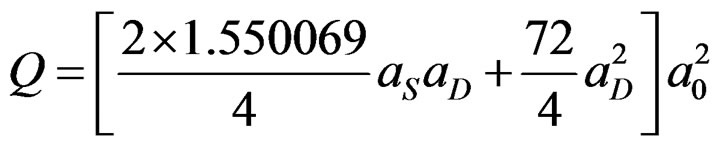 . (3.7)
. (3.7)
The estimation of the quadrupole moment of the deuteron is now possible if we now can fix the expansion coefficients 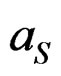 and
and 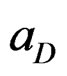 of the superposed wave function of Equation (3.2). These are given by,
of the superposed wave function of Equation (3.2). These are given by,
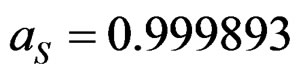 , (3.8)
, (3.8)
and,
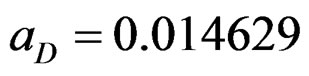 . (3.9)
. (3.9)
These expansion coefficients satisfy the following relation to conserve the probability.
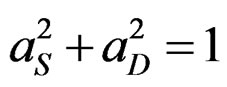 . (3.10)
. (3.10)
From the above the estimated value of the quadrupole moment of the deuteron is,
 . (3.11)
. (3.11)
The above result is obtained without assuming any tensor forces. We will now find the expectation value of the total Hamiltonian for the superposed state given by Equation (3.2).
 . (3.12)
. (3.12)
The above expectation value is −2.224677 MeV which is almost equal to the ground state energy of the deuteron in the s-state.
The operator for the magnetic moment μ of the Deuteron is given by.
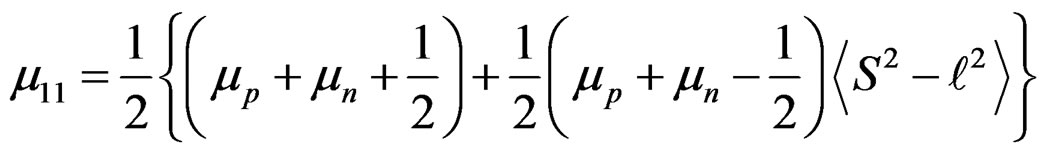 , (3.13)
, (3.13)
where S is the total spin quantum number and 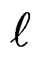 is the orbital angular quantum number. The expectation value of the above operator for the superposed state of Equation (3.2) is given by,
is the orbital angular quantum number. The expectation value of the above operator for the superposed state of Equation (3.2) is given by,
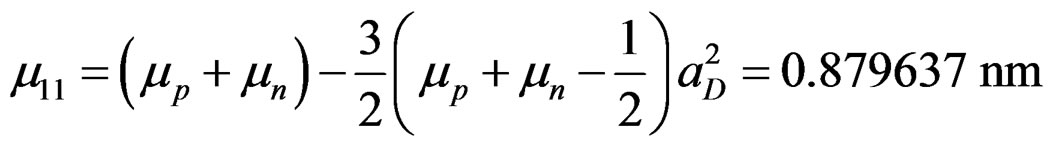 . (3.14)
. (3.14)
This value is no different from the sum of the two magnetic moments. The experimental value is about 0.85 nm. This value can be reproduced if we take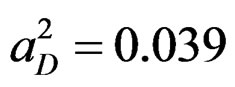 . But then the quadrupole moment will not be correct with this value of
. But then the quadrupole moment will not be correct with this value of . We believe that the quadrupole moment calculation is more correct because it is based on wave functions obtained by solving the equation. The answer for the magnetic moment should be found through relativistic extension of the model.
. We believe that the quadrupole moment calculation is more correct because it is based on wave functions obtained by solving the equation. The answer for the magnetic moment should be found through relativistic extension of the model.
4. MGPE for Some Nuclei
To show that the “Morphed Gravitational Potential Energy, (MGPE) is indeed correct we apply this potential energy to some more nuclei.
1) Triton nucleus is made up of one proton and two neutrons. The binding energy of this nucleus is [11]
8.4817 MeV. The total spin is J = +. The core for this nucleus mustbe a proton-neutron because this combination is more tight than a neutron-neutron binding [see 3]. Therefore the core mass 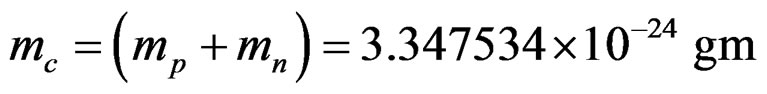 . The MGPE for this nucleus is,
. The MGPE for this nucleus is,
 , (4.1)
, (4.1)
where
 . (4.2)
. (4.2)
This value is obtained by comparing the ground state energy with the binding energy of this nucleus. The orbital angular momentum for the ground state must be zero for this nucleus. Hence the principal quantum number n = 1, 2, 3, etc. The energy Eigen values are given by
 , (4.3)
, (4.3)
where,
 . (4.4)
. (4.4)
2) The nucleus 2He3 contains two protons and a neutron. The binding energy of this nucleus is 7.178 MeV. and J = (1/2)+. So  for this nucleus. The core mass for this nucleus is also same as for the triton nucleus. The total potential energy in this case is given by,
for this nucleus. The core mass for this nucleus is also same as for the triton nucleus. The total potential energy in this case is given by,
 , (4.5)
, (4.5)
where,
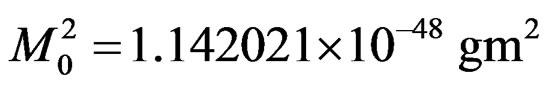 . (4.6)
. (4.6)
The energy spectrum for this nucleus is given by,
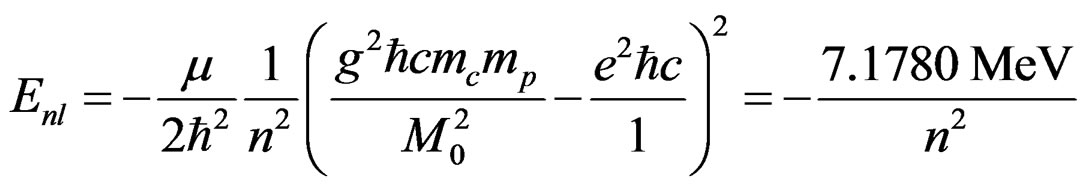 . (4.7)
. (4.7)
The reduced mass in this case is given by,
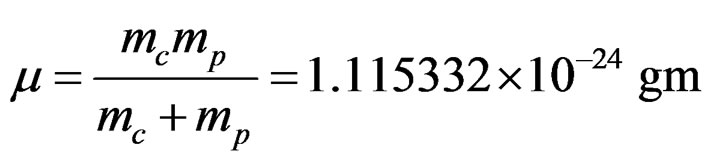 . (4.8)
. (4.8)
The principal quantum number for this nucleus is n = 1, 2, 3, It should be noted that Helium-4 and Helium-3 Nuclei have different values of M0 in the MGPE expressions.
3) The nucleus 3Li7 (Lithium) Has a binding energy of 39.2452 MeV and a J = (3/2)−. Therefore 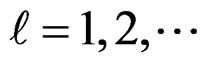 and the principal quantum number
and the principal quantum number 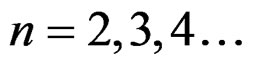 for this nucleus. The core of this nucleus consists of 3 protons and 3 neutrons and hence
for this nucleus. The core of this nucleus consists of 3 protons and 3 neutrons and hence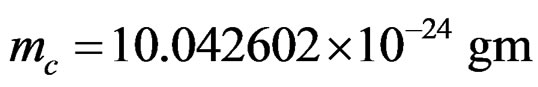 . There is a neutron outside this core and the Potential energy is given by,
. There is a neutron outside this core and the Potential energy is given by,
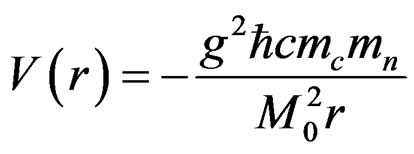 , (4.9)
, (4.9)
where, . (4.10)
. (4.10)
The energy spectrum for this nucleus is given by,
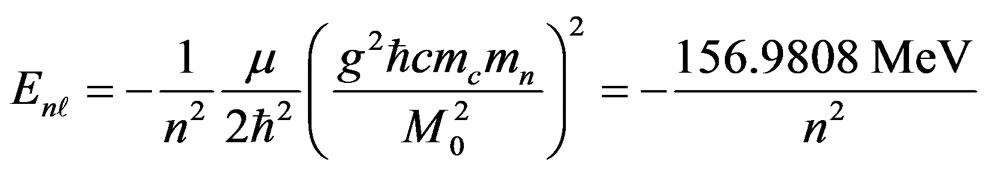 . (4.11)
. (4.11)
For this case the reduced mass is given by,
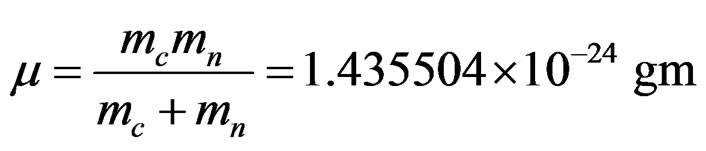 . (4.12)
. (4.12)
4) The binding energy of the Beryllium nucleus, 4Be9, is 58.1648 MeV. It has a spin J = (3/2)− and therefore the principal quantum number for this nucleus is 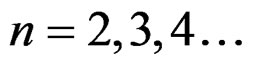 as in the case of Lithium. This nucleus has 4protons and 5 neutrons. The core part has a mass mc = 13.390136 × 10−24 gm and there is one neutron outside the core. The potential energy for this case is given by,
as in the case of Lithium. This nucleus has 4protons and 5 neutrons. The core part has a mass mc = 13.390136 × 10−24 gm and there is one neutron outside the core. The potential energy for this case is given by,
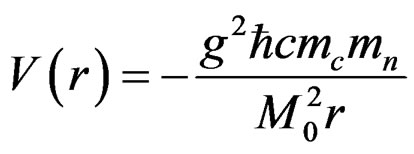 , (4.13)
, (4.13)
where,
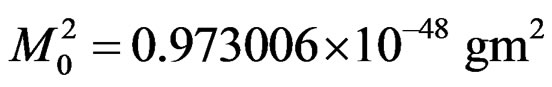 . (4.14)
. (4.14)
The energy spectrum for this nucleus is given by,
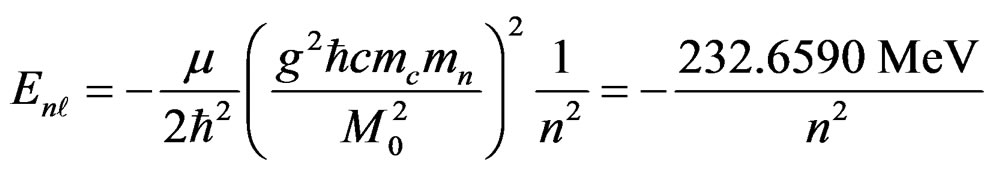 . (4.15)
. (4.15)
In this case the reduced mass is given by,
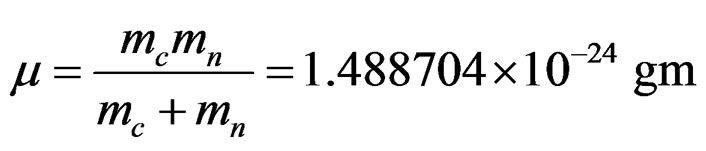 . (4.16)
. (4.16)
5) The beryllium-8 nucleus has 4 protons and 4 neutrons and it is very unstable and decays into two helium-4 nuclei. The binding energy of this nucleus is 56.5 Mev. We assume here that this nucleus is a bound system of two helium-4 nuclei and the total potential energy is given by,
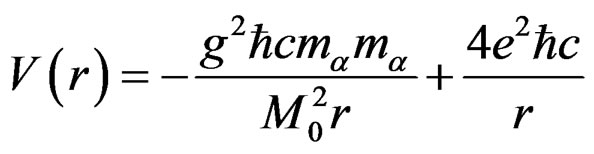 , (4.17)
, (4.17)
Where, 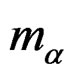 is the exact mass of the
is the exact mass of the 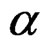 particle and is given by,
particle and is given by, 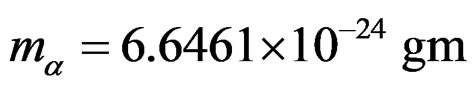 and the reduced mass is half of this. In the above expression the parameter
and the reduced mass is half of this. In the above expression the parameter 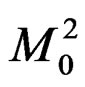 is given by,
is given by,
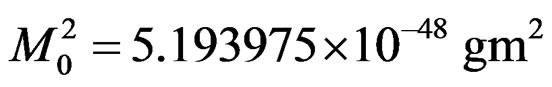 . (4.18)
. (4.18)
The energy spectrum in this case is given by,
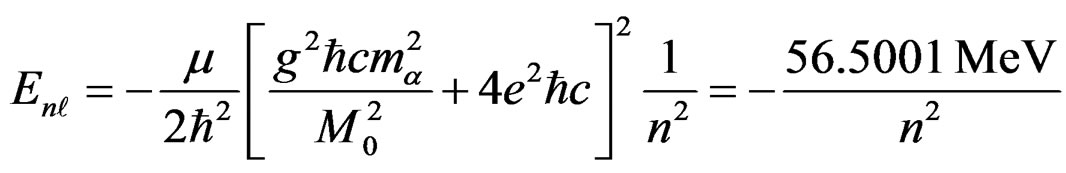 . (4.19)
. (4.19)
Here n = 1, 2, 3∙∙∙ is the principal quantum number.
5. Morphed Gravitational Potential Energy and the MCPE
In this paper, the MGPE along with the methods of quantum mechanics is used to estimate all the known experimental facts of the Deuteron nucleus. The estimated quadrupole moment agrees pretty well with the experiment. The Deuteron is supposed to have no excited states. But here n = 1 and n = 3 excited states are superposed to explain the quadrupole moment. The energy of the superposed state is almost identical to the ground state energy of the Deuteron. The parity conservation prohibits n = 2 and other excited states. A similar situation may exist in the case of other nuclei for which many possible energy levels are listed here. Finally, it should be noted that the parameter M0 is not a universal constant. It depends on the mass of the nucleus. The functional dependence of M0 on the interacting masses is unclear as of now.
There is an experimental fact which is quite often ignored. There is no object whose mass is zero but carries an electric charge. All charged particles have finite mass. Why is it necessary to have a finite mass in order to be electrically charged? It is this question that is ignored. The electrostatic PE between two charges 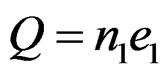 and
and 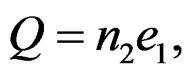 where
where 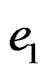 is the charge on the proton, and n1 and n2 are integers, which can be positive or negative is given by,
is the charge on the proton, and n1 and n2 are integers, which can be positive or negative is given by,
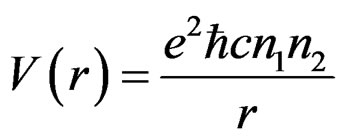 , (5.1)
, (5.1)
where 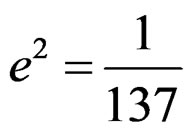 is the fine structure constant and it will take care of the system of units used. In the above expression the charged particle can have any mass including zero. To avoid this, we rewrite Equation (5.1) in the following way
is the fine structure constant and it will take care of the system of units used. In the above expression the charged particle can have any mass including zero. To avoid this, we rewrite Equation (5.1) in the following way
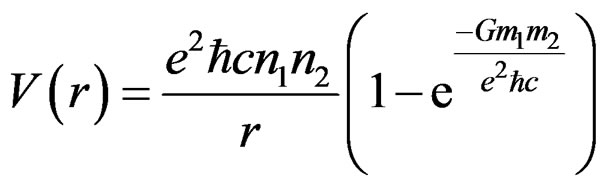 . (5.2)
. (5.2)
In the above expression, m1 is the mass of the particle whose charge is n1e1 and m2 is the mass of the particle whose charge is n2e1. The Coulomb potential energy given by Equation (5.2) will be zero if either mass is zero. Also, it will be zero whenever both the masses are zero. In other words, there will not be any Coulomb potential energy for zero mass particles. An approximation to Equation (5.2) is given by
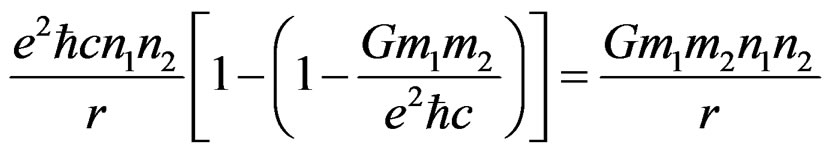 . (5.3)
. (5.3)
In spite of the appearances, the final expression is Coulomb potential energy. This is called the “Morphed Coulomb Potential Energy” (MCPE).
For an electron, the total potential energy is given by
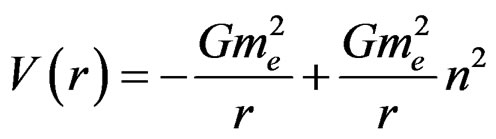 , (5.4)
, (5.4)
where the second term is the MCPE of the electron. The above total PE will be zero if n = ±1. By convention, we choose n = −1 for the electron. Similarly the morphed gravitational PE and the Coulomb PE add up to zero.
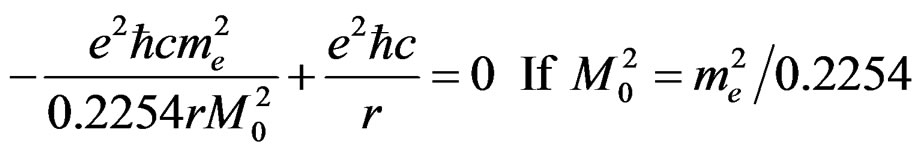 . (5.5)
. (5.5)
On a cosmic scale, the Morphed Coulomb PE and the gravitational potential energy between two Galaxies are given by
 , (5.6)
, (5.6)
where M1 and M2 are the masses of the galaxies whose electric charges are n1e1 and n2e1. Here, e1 is the charge of the proton and n1 and n2 are integers which can be positive or negative. Depending on these integers, the force can be repulsive, attractive or zero. Thus the universe can expand, contract or be stationary.
Finally, we point out one observation
 , (5.7)
, (5.7)
where 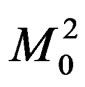 is given by Equation (2.3). This can be used to reexamine the Lamb shift.
is given by Equation (2.3). This can be used to reexamine the Lamb shift.
6. Acknowledgements
This work is supported by Ajitha Ganapathiraju, Seshu R Ganapathiraju and Prudhvi R Chintalapati. The author is very grateful to them.
REFERENCES
- H. A. Enge, “Introduction to Nuclear Physics,” AddisonWesley, Ontario, 1966.
- C. C. Raju, Journal of Modern Physics, Vol. 4, 2013, pp. 459-462.
- C. C. Raju, Journal of Nuclear and Particle Physics, Vol. 3, 2013, pp. 25-28.
- C. C. Raju, International Journal of Theoretical Physics, Vol. 36, 1997, pp. 2937-2939. doi:10.1007/BF02435719
- L. I. Schiff, “Quantum Mechanics,” McGraw-Hill, New York, 1955.
- G. Baym, “Lectures on Quantum Mechanics,” W.A. Benzamin, New York, 1969.
- E. E. Anderson, “Modern Physics and Quantum Mechanics,” W.B. Sanders, Toronto, 1971.
- R. R. Roy and B. P. Nigam, “Nuclear Physics,” WileyEastern, Delhi, 1979.
- R. J. Bin-Stoyle, “Nuclear and Particle Physics,” Thompson, India, 1991.
- M. L. Pandya and R. P. S.Yadav, “Elements of Nuclear Physics,” KedarNath Ram, Meerat, 1994.
- S. S. M. Wong, “Introductory Nuclear Physics,” Prentice Hall, India, 1996.

