Journal of Modern Physics
Vol.4 No.6A(2013), Article ID:33586,7 pages DOI:10.4236/jmp.2013.46A005
Could Superconductivity Contribute to the Saturn Rings Origin?
Modern Science Institute, SAIBR, Moscow, Russia
Email: chernyv@bk.ru
Copyright © 2013 Vladimir V. Tchernyi (Cherny). This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 13, 2013; revised May 16, 2013; accepted June 11, 2013
Keywords: Origin of Saturn Rings; Origin of Planetary Rings; Superconductivity of the Planetary Rings
ABSTRACT
The article shows how the phenomenon of superconductivity can contribute to the origin of Saturn rings. The main argument for this coming from the general physics consideration and based on the fact that Saturn has a magnetic field, and the temperature of the environment in its vicinity is low enough to think about superconductivity.
1. Introduction
Pyotr Kapitsa the Nobel Prize winner (1978) for the work in low-temperature physics said: “The worst in scientific work is triviality. The most important is not accuracy but novelty. Never miss a chance of publication of new ideas.” (Uspekhi Fizicheskih Nauk (Physics-Uspekhi), 1994, Vol. 164, p. 1326). So in this paper we have proposed an idea of contribution of the superconductivity to the Saturn rings origin.
Currently, there is no clear understanding of the origin of the Saturn’s rings. Two versions of the ring origin are known now. One assumes that the rings were originated when an asteroid-type body approached the Saturn and then was destroyed by gravity and centrifugal forces and subsequently the rings were created from the debris. The second idea assumes the rings are formed from the particles of the protoplanetary cloud around the Saturn. However, this model has not been fully developed yet. This paper proposes a novel mechanism how rings could originate from the frozen particles of the protoplanetary cloud after the formation of the magnetic field of the Saturn. The model is based on the electromagnetic interaction of ice-carbon superconductive particles with the planetary magnetic field.
The founder of the theory of electromagnetic waves, J. K. Maxwell in his award winning paper on the subject “On the stability of the motion of Saturn’s rings” (1859), deduces that the rings of the Saturn cannot be solid and the rings could be stable only if they consist of “an indefinite number of unconnected particles orbiting Saturn in much the same way as our Moon orbits the Earth” [1], gravitational forces otherwise would destroy them. Groundbased experiments and the data from Pioneer, Voyager 1, 2 and Cassini-Huygens space missions have revealed that the rings are composed of pure ice particles, and ice particles with carbon and other impurities.
After G. Galileo (1610), many researchers have studied the nature of the Saturn rings [for example, 1-16]. Different ring systems are morphologically quite distinct but all are shaped by a few common processes. This is the angular momentum transport of the rings particles by gravitational interactions between satellites, moons and ring matter. In fact, orbital resonances between satellites, moons and ring particles play an important role in forming a specific structure of the rings and gaps and enhancing the influence of the satellites. Moreover, extensive experimental data confirmed importance of magneto-hydrodynamic, plasma, and especially electromagnetic phenomena on the nature of the ring structure.
Despite rich database available, no physically satisfactory model of the Saturn rings exists yet, and many experimental data have no explanation.
Superconductivity of the ring particles may reflect the fact that the ring particles are relics of the early days of the Solar system, and the particles were never subject to coalescence and heating. Indeed, the Sun heats the rings weakly, so that the temperature in the area of the rings is about 70 - 110 K. Therefore, presence of superconducting substance may be possible in the space behind the belt of the asteroids. Although superconducting particles can form a relatively compact macroscopic structure formation, on short distances however, they weakly repel each other in presence of an external magnetic field (resembling a fluidized bed).
In 1933 W. Meissner and R. Ochsenfeld found that there is a complete ejection of magnetic field lines from the interior of the body as it transition into the superconducting state. The high-temperature superconductivity was discovered by Bednortz and Muller in 1986 [17]. In 1986 superconductivity of ice subjected to high pressure was experimentally demonstrated by A.N. Babushkin1 et al. [18]. High temperature superconductivity of a fullerene C36 has been conjectured recently by Grossman et al. [19]. Considering a 7% of a glassy carbon composition of Saturn rings, the superconductive properties of these rings are quite plausible.
We conjecture the proposed model [22-33] that assumes existence of a superconducting fraction of the particles forming the Saturn rings would allow enhancing classical theories of the planetary rings (gravitational, mechanical, magneto hydrodynamic plasma interactions).
An interesting point of this work is that even though its subject concerns a problem related to astronomy, the solution may come from laboratory scale experiments on an electromagnetic interaction for dust systems subjected to a static magnetic field (see, for example [20]).
2. Experimental Data Analysis
2.1. Thin Width and Sharp Edges of the Rings
Similarly to iron magnetic particles that create dense and rarefied regions in a non-uniform magnetic field, superconducting particles also form bands, looking from outside like a system of rings. Superconducting particles collapse into a system of rings as a result of their exchange between the areas of a smaller magnetic field, within the plane of the magnetic equator, with the force: F = −mdH/dz, where m—the magnetic moment of the particle, dH/dz—the gradient of the magnetic field along the z axis of the magnetic dipole. The force of the diamagnetic expulsion forms sharp edges of the ring: F = −mdH/dy, where dH/dy—the gradient of the magnetic field along the radius of the ring. The accidental break in the ring will be stabilized by the force of the diamagnetic expulsion F = −mdH/dx, where dH/dx—gradient of the magnetic field in the tangential direction. The image of the magnetic field line deformation measured for the ring F by the Pioneer mission [5,6,12] looks like the image of the magnetic field expulsed from the ring. It is of the same nature as for the well-know case of a small superconducting ceramic sample pushing out its own internal magnetic field, under the low temperature from the contact with liquid nitrogen [17].
2.2. Planetary Radial Dust Flow
Superconducting material is characterized by the London’s penetration depth lL of the magnetic field [17]. For particles of sizes comparable with the London’s penetration depth, the influence of the magnetic field on superconductivity becomes appreciable. Smaller particles do not couple to the planetary magnetic field, because they loose their superconductivity due to their small size. Dynamics of these particles is different from dynamics of particles with larger size, >2lL. Small particles will fall down to the planet due to gravity. Thus, existence of a radial planetary dust flux composed of submicron’s size particles is related to a lack of superconductivity of the ring particles due to their small size. It is also possible for the particles to loose their superconductivity by collisions and by magnetic field fluctuations.
2.3. The Azimutal Brightness of the Saturn A Ring
Present understanding of this phenomenon is based on: 1) the assumption of a synchronous rotation of the ring’s particles with their asymmetrical form as extended ellipsoids directed under a small angle to the orbit; 2) existence of an asymmetrical albedo of the surface [5,6,12]. Consider now our SIP model for this phenomenon. If a superconductor is placed in the magnetic field, a magnetic moment directed oppositely to the external field is induced. The matter is magnetized, not along the external magnetic field but in the opposite direction. A superdiamagnetic ring particle in a form of a rod attempts to align itself perpendicularly to the magnetic field lines. It is a known fact from the science on ice [21], that growing snowflakes at temperature below –22˚C take a form of prisms. Thus, the prism of the superconducting ice particle will be oriented perpendicularly to the field lines of the poloidal and toroidal components of the magnetic fields of the Saturn. It becomes now clear that the variable azimutal brightness of the Saturn’s rings system A is related to the orientation of the elongated ellipsoid of the superconducting particles versus the direction of the planetary magnetic field.
2.4. The Saturn Ring B Spokes
The Saturn ring B spokes as well as the spokes of any wheel, are aligned nearly radially. The size of the spokes is about 104 km along the radius and about 103 km along the orbit of the ring. The matter of the spokes consists of the micron and submicron size particles [11]. There were many attempts to explain the nature of these spokes. Generally, all the models are based on the action of the force of gravity. Nevertheless a different idea was put forward that Registration of rotating spokes is perhaps related to the electromagnetic force. Analysis of the spectral radiation power of spokes provides a specific periodicity about 640.6 ± 3.5 min, which almost coincides with the period of rotation of the magnetic field of Saturn (639.4 min). Moreover, a strong correlation of maxima and minima of activity of spokes with the spectral magnetic longitudes is connected to presence or absence of the radiation of Saturn’s Kilometric Radiation (SKR). It enforces the assumption of the dependence of the spoke dynamics on the magnetic field of Saturn and testifies to the presence of large-scale anomalies in the magnetic field of Saturn. We can suggest the following explanation of it. Superconducting ice particles of the ring matter are orbiting in accordance with the Kepler’s law and have own speed on each orbit. Further, a magnetic field of Saturn has its own anomalies along some radial direction from the planet.
When the particles enter into this anomalous region, the force of diamagnetic expulsion applied to the particles, changes. The particles begin to change their orbit. For a significant number of participating particles, this process for the external observer appears as a turbulent cloud stretched along the radius in a form of a spoke. After passing the anomaly, particle return to their prior orbit and the common appearance of the rings is recovered.
2.5. High Reflection and Low Brightness of the Rings Particles in the Radiofrequency Range
We can explain also using our superconductivity model. Discovery in 1973 of a strong radar-tracking reflection from the rings of Saturn was surprising [5,6,12]. It turned out that the rings of the Saturn actually have the greatest radar-tracking section among all bodies of the Solar system. It was explained by assuming a metallic nature of the particles. The data of the Voyager excludes this possibility. The disk of superconducting particles completely reflects radiation with frequencies below 1011 Hz and poorly reflects radiation with higher frequencies, as in the case of a superconductor. The superconductors have practically no electric resistance up to frequencies of 100 MHz. A threshold is at the frequency of about 100 GHz, and above it a fast quantum phenomena causes a sharp increase of resistance, as it is shown on Figure 1. Hence a specific characteristic of brightness follows.
2.6. Intrinsic Wide Band Pulse Radiation of the Rings
Data from Voyager have shown that the rings radiate intrinsic wide band pulse radiation within the 20 KHz - 40.2 MHz [5,6,12]. These waves probably are the result of an interaction of charged particles with the particles of ice and friction of ice particles when the costriking occurs. These incidental radio discharges are called Saturn’s Electrostatic Discharges (SED). The average period
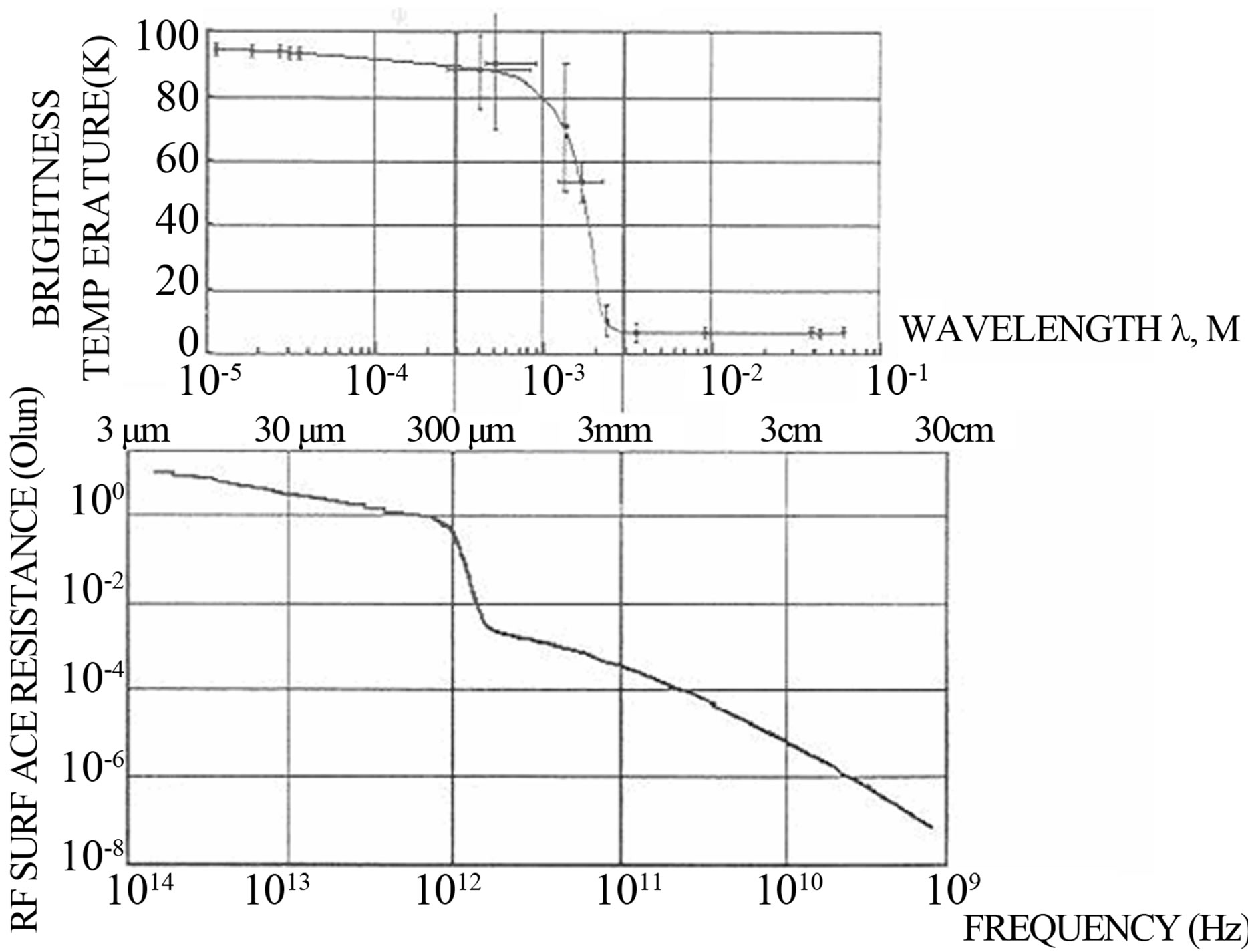
Figure 1. The top diagram is the dependence of the brightness temperature of the rings on the wavelength: the transition from the radiation of the almost black body to practically a complete reflection is observed [5,6,12]. The bottom diagram is dependence of the surface resistance of the superconductor on frequency for Nb at T = 4.2 K [17].
of SED is well determined and was established as 10 hour 10 ± 5 min and 10 hour 11 ± 5 min by Voyager-1, -2. If the ring has a source of SED, the area of this source can be located at the distance of 107,990 - 109,000 km from the planet according to the measured periodicity. Experimental data for SKR, SED and spokes activity are specifying electromagnetic coupling between the planetary ring system and the magnetosphere of the planet. In accordance with considering electromagnetic model, when particles with superconductivity are approaching to the distance about 10−8 m, or if they have a dot contact, it creates superconducting transition between them, and electrons can be tunneled through it. And consequently this type of weak link starts to generate electromagnetic radiation—nonstationary Josephson phenomenon [17,20-33]. The radiation frequency is proportional to the junction voltage, ν = 2 eV/h, where 2e/h = 483.6 MHz/µV, e is a charge of electron, h is Plank constant.
2.7. Frequency Anomalies of Thermal Radiation of the Rings in the 100 µm - 1 cm Range
The measured brightness temperature for the short wavelengths is less than the true brightness temperature of the rings, and for the longer wavelengths, the rings look much colder than in the case when the radiation corresponds to their physical temperature [5,6,12]. Within the range 100 µm - 1 mm the brightness temperature of the ring (Figure 1) sharply falls below the black body characteristics. For the wavelengths longer than 1 cm a ring behaves as the diffusion screen, reflecting planetary and cold space radiation. The central part of the spectral range 100 µm - 1 cm is the most sensitive part of dependence which may contain the important information for the fundamental properties of the substance of the particles. Following our model, for a superconducting condition, the electrons do not interact with the crystal lattice and do not exchange energy with it; therefore they cannot transfer heat from one part of the body into another. Hence, when the substance passes into a super conducting condition, its heat conductivity is lowered. And under temperatures significantly below critical there are very few ordinary electrons capable of transferring heat [20-33].
2.8. Color Difference of Rings on Small Scale
The balance of the three forces determines the position of the superconducting particles in the gravitational and magnetic planetary fields: gravitational force, centrifugal one and diamagnetic expulsion, Figure 1. Following our model, we consider the distribution of three particles (a, b, c) with equal weights and on close orbits. Let the particle a be entirely superconducting pure ice, b—the iced particles with impurity of clathrate-hydrates of ammonia or methane (NH3; CH4 H2O), c—ice particles with impurities of sulfur and iron containing silicates (H2S). Each impurity provides its own contribution to the superconductivity phase and it will determine the color of the particle. The force of a diamagnetic expulsion—FL. Therefore for each of the considered particles the balance of the three forces on the orbit has a different value.
2.9. Anomalous Inversed Reflection of Circularly Polarized Microwaves for Wavelengths above 1 cm
The study of reflection of radiowaves with wavelength more than 1 cm, from the rings, has been made with ground based radar and with the space probe [5,6,12]. The reflection appears rather large, and the geometrical albedo is equal approximately to 0.34 and has no strong functional dependence on the wavelength or on the angle of the inclination of the ring’s pitch. The rings are strong depolarizers. Therefore, in order to get any information from the reflection it is necessary to measure a reflected signal on two orthogonal polarizations separately. The reflected portion of the signal of the same polarization as the incoming signal is called the signal of “observed” polarization. The perpendicular component is called a signal of “unobserved” polarization. Difference between these two signals provides information about so called factor of polarization which indicates polarization properties of the object. For the planets of the solar system usually reflected signal on unobserved polarization is small. As to the Saturn’s rings for the same range of wavelengths and angles of inclination of incident wave factor of polarization becomes to be much bigger. It may have an explanation coming from the theory of electromagnetic waves reflection from a superconductor. The superconductors are differs significantly from the ideal conductors, they have almost infinite conductivity, and they also demonstrate an ideal diamagnetism. For the situation with the reflection from the iced rings particles having superconductivity it means that if the incident wave of the radar signal with circular polarization has certain chirality, then the same chirality should be for the reflected wave.
2.10. An Atmosphere of Unknown Origin at the Rings
The atmosphere of Saturn’s rings can originate as a result of a fine balance of forces of gravitational attraction and diamagnetic expulsion of gas molecules. Levitation of gas molecules may be presented as a result of its diamagnetic expulsion from superconducting particles due to induced magnetic moments by a magnetic field of the planet. A similar situation can be observed under laboratory conditions when an atmospheric water steam is precipitated on substance as a white-frost at the transition point of the substance from the superconducting into a conventional state.
2.11. Existence of Waves of Density and Bending Waves within the Rings
The existence of waves of density and bending waves in the Saturn’s rings has no complete explanation based only on gravitational phenomena. Let’s consider our SIP model. Note that the external magnetic field is directed along a free surface of a diamagnetic fluid representing a disk of the rings. Consider a localized deformation of the disc surface at some point of the ring. It can be induced, for example, by fluctuating gravitational forces of Saturn moons or satellites, or due to plasma/magnetohydrodynamic effects. Then a ponderomotive force will be created and applied in the opposite direction to preserve an original disc surface. Therefore, the planetary magnetic field enhances the stiffness and stability of the disc surface.
3. Theoretical Treatment of the Saturn’s Rings Origin
We will demonstrate now how Saturn rings could originnate from the ice particles located within the protoplanetary cloud, following our simple electromagnetic model. We assume that prior emergence of the Saturn magnetic field all the particles within the proto-planetary cloud are located on the Keplerian orbits, exhibiting a balance of the force of gravity and the centrifugal force. With emergence of the Saturn magnetic field, the superconducting particles of the proto-planetary cloud begin to demonstrate an ideal diamagnetism (Meissner-Ochsenfeld phenomenon). Particles begin to interact with the magnetic field and all the particles become to be involved in an additional azimuth-orbital motion. Let’s estimate the result of this motion.
If the magnetic field of the planet is H, and the planetary magnetic moment is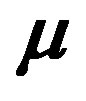 , then the magnetic field at any particular point within the proto-planetary cloud, located at the distance
, then the magnetic field at any particular point within the proto-planetary cloud, located at the distance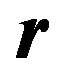 , can be presented as:
, can be presented as:
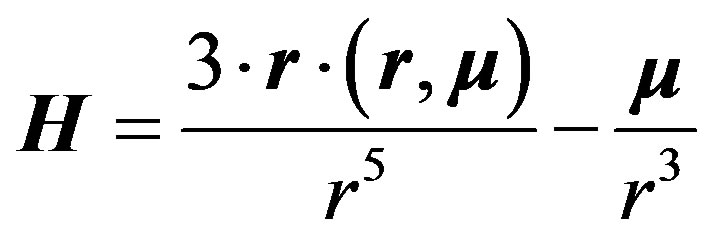 (3.1)
(3.1)
Then the superconducting sphere of the radius R, located within the proto-planetary cloud, acquires the magnetic moment
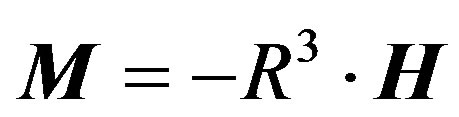 (3.2)
(3.2)
That energy of a superconductor in a magnetic field is:
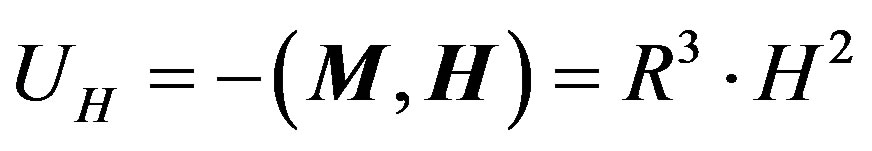 (3.3)
(3.3)
We place the origin of the coordinates at the center of a planet, and the axis z direct along the magnetic moment of a planet (orthogonal to equator). Then the magnetic energy will become:
 (3.4)
(3.4)
Here —the angle between the vector
—the angle between the vector  and the axis Z. It can be seen from the expression (3.4), that the magnetic energy of the superconducting particle has a minimum value when the radius-vector
and the axis Z. It can be seen from the expression (3.4), that the magnetic energy of the superconducting particle has a minimum value when the radius-vector 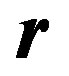 (the position of the superconducting particle) is in a plane of the magnetic equator, perpendicular to the axis Z
(the position of the superconducting particle) is in a plane of the magnetic equator, perpendicular to the axis Z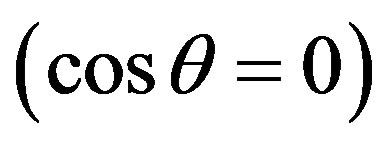 . Consider now one particle. Evidently, its trajectory (orbit) in the azimuth-orbital direction can only be disturbed by the magnetic field. However, in case of a significant amount of particles, resembling the proto-planetary cloud, after a transient time, collisions between particles will compensate their azimuth-orbital movements, and, as a result, eventually, during some time, all orbits of the particles of the proto-planetary cloud should come together to the magnetic equator plane and create highly flattening disc around the planet. Within the disc of rings, all particles will be located on the Keplerian orbit, where there is a balance of gravity, centrifugal and electromagnetic forces. At the same time, orbital resonances (due to a gravity force) between satellites, moons and the ring particles play an important role in forming a specific structure of the rings and gaps.
. Consider now one particle. Evidently, its trajectory (orbit) in the azimuth-orbital direction can only be disturbed by the magnetic field. However, in case of a significant amount of particles, resembling the proto-planetary cloud, after a transient time, collisions between particles will compensate their azimuth-orbital movements, and, as a result, eventually, during some time, all orbits of the particles of the proto-planetary cloud should come together to the magnetic equator plane and create highly flattening disc around the planet. Within the disc of rings, all particles will be located on the Keplerian orbit, where there is a balance of gravity, centrifugal and electromagnetic forces. At the same time, orbital resonances (due to a gravity force) between satellites, moons and the ring particles play an important role in forming a specific structure of the rings and gaps.
4. Separation and Collision of the Particles within the Sombrero of Rings
We can define the energy of the interaction of two superconducting particles with magnetic moment m1 and m2 located at positions r1 and r2, respectively as:
 , (4.1)
, (4.1)
The magnetic field H2 induced by the magnetic moment m2 can be presented as
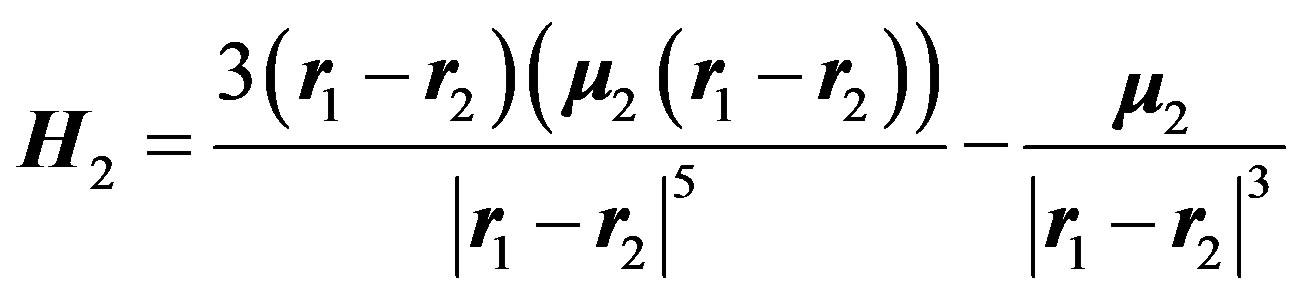 (4.2)
(4.2)
If the particle with the magnetic moment m2 is placed at the origin (r2 = 0), then the expression for the energy of the interaction of two particles (4.1) will read:
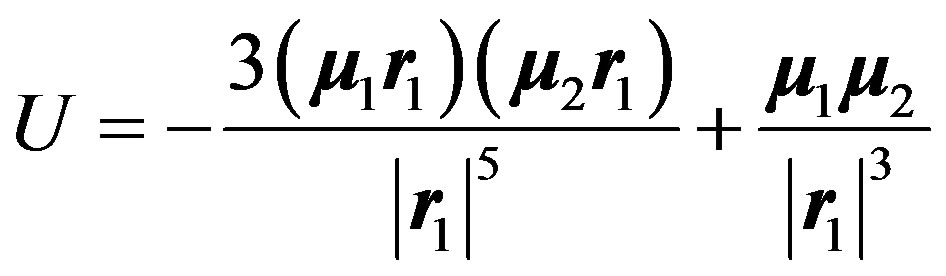 (4.3)
(4.3)
The planetary magnetic field in the plane of the Saturn rings coincides with the planet rotation axis. For the axis Z directed along the rotation axis of the planet, the magnetic moment of the particles will also be directed along the axis Z. Using a cylindrical system of coordinates 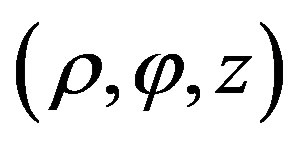 we can represent expression (4.3) as:
we can represent expression (4.3) as:
 (4.4)
(4.4)
Let us use the expression (4.4) to estimate the interaction of two superconducting particles for two different cases. The first one corresponds to two particles located in the same plane within the sombrero of the rings (Z = 0), and the second situation is for two particles located on the different planes but on the same axis .
.
From the expression (4.4), it follows that for the particles with the magnetic moments  and
and 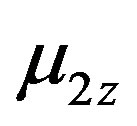 located on the same plane, Z = 0, we get the energy of their interaction:
located on the same plane, Z = 0, we get the energy of their interaction:
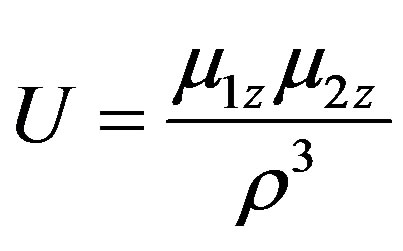 , (4.5)
, (4.5)
From the expression (4.5), it follows that in this situation both particles will be repelling each other and they will maintain a separation distance between them. This result has been confirmed by the data of Cassini mission: the particles are separated2.
For the second case, both particles are located on the same axis but on different planes, and, as it follows from (4.4), the expression for the interaction energy is:
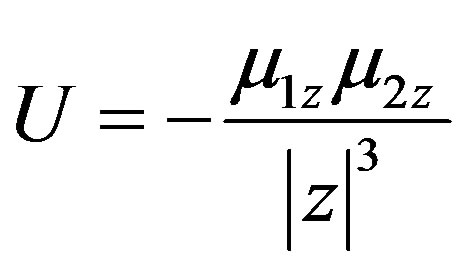 , (4.6)
, (4.6)
We can see that in this case both particles attract each other; they could even collide or stick together and form bigger pieces or lumps of ice. This fact has an experimental conformation by the Cassini mission. As we know from the data of the Cassini mission, the particles within the sombrero of the rings can collide or even stick together and form bigger pieces of ice3. Then, later on, the particles within 50 meters or more in diameter can be shattered into smaller pieces by a combined action of gravity and centrifugal force.
5. Conclusions
Analysis of experimental data for Saturn’s rings points to the conjecture that the particles constituting the rings may be superconductive. Moreover, it can be theoreticcally argued that the Saturn rings could originate from the proto-planetary particle cloud if particles were superconductive. The ring emerges some time after the magnetic field of the planet is being formed. It can be a result of the interaction of the superconducting carbon doped ice particles of the protoplanetary cloud with the nonuniform magnetic field of the Saturn. After a transient, all Kepler’s orbits of the particles become to be localized in the plane of the magnetic equator (which is almost coincides with the geographical equator of Saturn), where the magnetic particle energy is minimum. Therefore, all orbits of the superconducting particles within sombrero disk of the rings are located within the magnetic equator plane. Then system of rings and gaps within sombrero of the rings was finally formed under influence of gravity resonances organized by the big amount of satellites located inside of the Saturn system. This process may take from thousands to million years.
Electromagnetism and superconductivity allow us to understand why planetary rings in the solar system appear only behind the belt of asteroid for the planets with the magnetic field and low temperature in their environment of their vicinity: Jupiter, Saturn, Uranus and Neptune. Presented superconducting ice particle model allows us to enrich the classical theories of the Saturn’s rings origin taking into account gravitational, mechanical, magnetohydrodynamic and plasma interactions. It becomes also possible to understand why there are no rings for the Earth, why there is a pulse electromagnetic radiation of the rings in the 20.4 kHz - 40.2 MHz range, and how “spokes” in the ring B are forming, etc.
6. Acknowledgements
The author would like to express greatest thanks for support, valuable discussions and advices to Professor Evgeny P. Bazhanov (Moscow), Tom V. Zaitsev, Valery A. Dybov, Evgeny V. Chensky, Andrew Yu. Pospelov, and special thanks to Olga I. Chernaya, Alicia Pagliere, Naomi Tchernyi, Raisa Chernousova, the Founder of The Electromagnetic Academy—MIT Professor Jin Au Kong, Professor Guennadi A. Kouzaev at Norwegian University of Science and Technology in Trondheim, Professor Youri V. Shestopalov at Karlstad University in Sweden, Professor Evgeny I. Nefyodov at Kotel’nikov Institute of Radioengineering and Electronics of RAS in Moscow, Professor Galina S. Makeeva at Penza State Technical University in Russia, Professor Aleksander G. Zadokhin in Moscow, University Professor John R. Whinnery and Professor Ture K. Gustafson at EECS University of California at Berkeley, Professor Essam A. Marouf at San Jose State University, Professor Peter Goldreich at Caltech, Professor Martha Pardavi-Horvath at John Washington University and National Bureau of Standard in Washington DC, Professor D. A. Mendis at University of California in San Diego, Dr. Konstanty Mazuruk at the University of Alabama in Huntsville, Professor Warren Pickett and Professor Richard Freeman at University of California at Davis. The author is also grateful for fruitful discussions to all participants of the seminars and conferences: NASA Marshall Space Flight Center and Huntsville Space Physics Colloquium; Institute for Astronomy at the University of Hawaii; Center for Astrophysics and Space Sciences at University of California in San Diego; Electrical Engineering and Computer Sciences Department at University of California in Berkeley; Department of Physics and Applied Science at University of California in Davis; Institute of Astronomy and Physics at La Plata, Buenos Aires; Progress in Electromagnetic Research Symposium (PIERS) organized by MIT; 42nd-50th SPIE Annual Meetings; the National Bureau of Standard in Washington DC; 30th Annual Meeting of the Division of Planetary Sciences at American Astronomical Society and The Central Astronomical Observatory of the Russian Academy of Sciences at Pulkovo.
REFERENCES
- J. C. Maxwell, S. G. Brush, C. W. F. Everitt and E. Garber, “Maxwell on Saturn’s Rings,” MIT Press, Cambridge, 1983.
- V. S. Safronov, “Evolution of Protoplanetary Cloud and Formation of the Earth and Planets,” Nauka, Moscow, 1969.
- R. M. Goldstein and G. A. Morris, Icarus, Vol. 20, 1973, pp. 249-283. doi:10.1016/0019-1035(73)90002-X
- M. L. Kaiser, V. D. Desch and F. Lecacheus, Nature, Vol. 292, 1981, pp. 731-733. doi:10.1038/292731a0
- A. Brahic, “Planetary Rings,” Copadeus, Toulouse, 1984.
- R. Greenberg and A. Brahic, “Planetary Rings,” University of Arizona Press, Tucson, 1984.
- A. N. Bliokh and V. V. Yaroshenko, Nature, Vol. 79, 1991, pp. 19-25 (In Russian).
- L. J. Spilker, “The Cassini-Huygens Mission to Saturn and Titan,” Caltech, Washington DC, 1997.
- L. Rowan, A. Sanchez-Lavega, T. I. Gombosi, K. S. Hansen, C. C. Porco, F. M. Flasar, L. W. Esposito, D. A. Gurnett, J. H. Waite Jr., D. T. Young, M. K. Dougherty, S. M. Krimigis, S. Kempf, et al., Science, Vol. 307, pp. 1222-1276. doi:10.1126/science.307.5713.1222
- H. Alfven, “Cosmic Plasma,” D. Reidel Publishing Co., Dordrecht, 1981. doi:10.1007/978-94-009-8374-8
- H. Alfen, Astrophysics Space Science, Vol. 97, 1983, pp. 79-94. doi:10.1007/BF00684612
- D. A. Mendis, J. R. Hill, W. H. Ip, C. K. Goertz and E. Grun, “Electrodynamics Processes in the Ring System Saturn,” In: T. Gehrels and M. Mathews, Eds., Saturn, University of Arizona Press, Tucson, 1984, pp. 546-589.
- L. W. Esposito, J. N. Cuzzi, J. B. Holberg, E. A. Marouf, G. L. Tyler and C. C. Porco, “Saturn’s Rings, Structure, Dynamics and Particle Properties,” In: T. Gehrels and M. S. Matthews, Eds., Saturn, University of Arizona Press, Tucson, 1984, pp. 463-545.
- N. N. Gor’kavyi and A. M. Fridman, “Physics of the Planetary Rings: Celestial Mechanics of Continuous Medium,” Nauka, Moscow, 1994.
- B. I. Rabinovich, Reports of the Russian Academy of Sciences (Dolklady RAN), Vol. 351, 1996, pp. 335-338.
- B. I. Rabinovich, Reports of the Russian Academy of Sciences (Doklady RAN), Vol. 367, 1999, pp. 345-348.
- V. L. Ginzburg and E. A. Andryushin, “Superconductivity,” World Scientific, Singapore City, 2004.
- G. V. Babushkina, L. Ya. Kobelev, E. N. Yakovlev and A. N. Babushkin, Physics of Solid State, Vol. 28, 1986, pp. 3732-3734.
- M. Côté, J. C. Grossman, M. L. Cohen and S. G. Louie, Physical Review Letters, Vol. 81, 1998, p. 697. doi:10.1103/PhysRevLett.81.697
- T. Yokota, IEEE Transactions on Plasma Science, Vol. 29, 2001, p. 279. doi:10.1109/27.923708
- N. Maeno, “Science about Ice,” Mir, Moscow, 1988.
- A. Yu. Pospelov, V. V. Tchernyi and S. V. Girich, “Planet’s Rings: Super-diamagnetic Model and New Course of Investigations,” Proceedings of SPIE 42nd Annual Meeting, San Diego, 27 July-1 August 1997, Vol. 3116, pp. 117-128.
- S. V. Girich, A. Yu. Pospelov and V. V. Tchernyi, Bulletin of the American Astronomical Society, Vol. 30, 1998, p. 1043.
- A. Yu. Pospelov, V. V. Tchernyi and S. V. Girich, “Are Saturn’s Rings Superconducting?” Progress in Electromagnetic Research Symposium (PIERS), Cambridge, 5-14 July 2000, p. 1158.
- V. V. Tchernyi and A. Yu. Pospelov, “Possible Role of Space Electromagnetism for Saturn’s Rings Existence,” Progress in Electromagnetic Research Symposium (PIERS), Honolulu, 13-16 October 2003.
- V. V. Tchernyi and A. Yu. Pospelov, Progress in Electromagnetic Research (PIER), Vol. 52, 2005, pp. 277- 299.
- V. V. Tchernyi and E. V. Chensky, Journal of Electromagnetic Waves and Applications, Vol. 19, 2005, pp. 1997-2006. doi:10.1163/156939305775570440
- V. V. Tchernyi and E. V. Chensky, IEEE Geoscience and Remote Sensing Letters, Vol. 2, 2005, pp. 445-446. Corrections, IEEE GRSL, Vol. 3, 2006, p. 281. doi:10.1109/LGRS.2005.852767
- V. V. Tchernyi (Cherny), “Prikladnaya Fizika,” Applied Physics, Vol. 12, 2006, pp. 10-16 (In Russian).
- V. V. Tchernyi and A. Yu. Pospelov, Astrophysics and Space Science, Vol. 307, 2007, pp. 347-356. doi:10.1007/s10509-006-9054-7
- V. V. Tchernyi, “Origin of the Saturn Rings: Electromagnetic Model of the Sombrero Rings Formation,” In: J. H. Denis and P. D. Aldridge, Eds., Space Exploration Research, Series: Space Science, Exploration and Policies, Nova Science Publishers, Hauppaugge, 2009, pp. 261-275.
- V. V. Tchernyi, Journal of Magnetohydrodynamics, Plasma and Space Research, Vol. 14, 2009, pp. 385-398.
- V. V. Tchernyi, “Discovery of Initial Formation (Origin) of the Sombrero Rings of Saturn: Role of Electromagnetism,” International Astronomical Union 27th General Assembly, Rio de Janeiro, 3-14 August 2009.
NOTES
1Professor Aleksey N. Babushkin is a Dean of the Physics Department at the Ural State University, Yekaterinburg, Russia.
2http://pds-rings.seti.org
3saturn.jpl.nasa.gov/multimedia/images/index.cfm

