ABSTRACT

Dark matter was first suspected in clusters of galaxies when these galaxies were found to move with too high a speed to be retained in the cluster by their gravitational influence on each other. Some current theories favor cold dark matter models where particles are created with low velocity dispersions and thus would become trapped in baryonic gravitational potentials. According to the standard Big-Bang model, dark matter is of nonbaryonic origin, otherwise the observed abundance of helium in the Universe would be violated. In this work, recent theoretical and observational developments are used to form a consistent picture of the events in the early Universe that gave rise to dark matter. According to the model that will be presented in this paper, supersymmetry plays a major role. In addition, the possibility that dark matter evolves in a spacetime manifold different from that of the observed Universe is discussed.

1. Introduction

During the last two decades, dark matter (DM) has occupied a pioneering position in research concerning cosmology and theoretical physics. There is compelling evidence that about 90% of the mass of the Universe is invisible, that is, it neither emits nor absorbs electromagnetic radiation. Data implying nonluminous matter surfaced in the 1930s. The first glimpse came when Oort analyzed the Doppler shift in the spectra of stars in the galactic disk and concluded that the mass of visible stars cannot explain the amount of gravitating matter implied by the measured velocities [1]. This finding was then confirmed by Zwicky who, by observing the Coma Cluster of galaxies, concluded that the velocity dispersions in rich clusters of galaxies require a huge amount of mass to keep them bound than could be accounted for by the luminous galaxies themselves [2]. The strongest evidence for dark matter comes from studies of the mass of individual galaxies. Mass estimates of individual galaxies can be obtained from the velocity dispersions or rotation curves of stars and gas making up the galaxy itself, or from the positions and velocities of globular clusters and satellite galaxies. Although these rotation curves trace the disk, several lines of argument strongly suggest that much of the nonluminous mass is in the spherical component that makes up the galactic halo [3-7].

Several models have been proposed to explain the origin of dark matter. Weakly interacting massive particles (WIMPs) and massive compact halo objects (MACHOs) are the prime candidates [8,9]. The proposal of WIMPs as a potential candidate is motivated by the fact that primordial nucleosynthesis provides only 0.2 of the cosmological density parameter (Ω₀ = ρ/ρ_C = 0.2), whereas inflationary theory and observational evidence suggest Ω₀ = 1 [10-12]. The MACHOs’ approach is based on finding a more natural explanation for DM using microlensing techniques. This approach, as we are going to see, may prove to be an invaluable tool for investigating the possibility of DM clumps in the galactic halo. Other potential DM candidates, such as primordial black holes and holeums, will also be discussed. Modified Newtonian dynamics (MOND) was a new approach that was proposed as a modification of Newton’s law of gravity to explain the galactic rotation curves [13], and it will be briefly described in this paper.

Recently, new strategies have been developed to directly observe DM by mapping its distribution in the Universe through its gravitational interaction with ordinary matter. Moreover, models and observational data give strong hints about the origin of DM [14,15].

The primary motivation for this paper is twofold: 1) to highlight the difficulties associated with the existing models that attempt to explain the nature and origin of DM. 2) to discuss some possible theoretical frames, supported by recent theoretical and observational data, in order to have a deeper understanding of the origin of DM and the associated problems.

2. Observational Evidence for Dark Matter

Observational evidence for dark matter has a long history starting with the work of Jan Oort and Fritz Zwicky in the early 1930s. In 1932, while studying the spectra of nearby stars in the Milky Way Galaxy, Oort noticed that the Doppler shifts of these stars indicated velocities that were too high to be accounted for by ordinary visible matter. In fact, the stars were moving so fast that they should have escaped from the Galaxy. Since the stars were clearly bound to the galaxy, Oort suggested that there must be additional, nonvisible matter in our Galaxy. Shortly after that, in 1933, Fritz Zwicky reached a similar conclusion while studying the velocities of galaxies in the Coma Cluster [16]. By measuring the velocities of galaxies near the edge of the cluster and making use of the virial theorem which states that

(1)

where 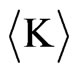and are the system’s mean kinetic and potential energies, respectively, and where it is understood that the system has reached equilibrium or steady-state, Zwicky was able to estimate the cluster’s total mass, which turned out to be approximately 400 times that of the luminous mass. Thus, Zwicky concluded that there must be a huge amount of nonvisible matter holding the cluster together [16].

Much later, in the 1960s and 1970s, work by Vera Rubin and her collaborators led to new observational evidence for dark matter. Rubin investigated the rotation curves for edge-on spiral galaxies, and surprisingly found flat rotation curves that extended all the way to the edges of the galaxies [17]. To appreciate why these observations were completely unexpected, consider a star of mass m orbiting at a distance r from the center of a spiral galaxy with a velocity v. From Newtonian mechanics

(2)

where M_r is the galaxy’s mass contained within the star’s orbit, and G is the gravitational constant. Solving for M_r and then differentiating with respect to r, we obtain

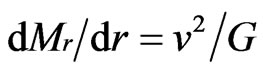(3)

But for a spherically symmetric system, the mass continuity equation gives

(4)

where r(r) is the mass density as a function of orbital distance. By equating Equations (3) and (4) we obtain

(5)

which indicates that the density varies as r^-2, whereas the observed number density of visible stars seems to fall off much more sharply, specifically as r^-3.5. To reconcile this discrepancy, one needs to invoke the existence of nonluminous or dark matter.

Building on the work of Rubin, other investigators studied the velocity dispersions of elliptical galaxies. The velocity dispersion, s, refers to the range of velocities about some mean value. The results obtained by different groups were in line with those of Rubin, and again pointed to the existence of large amounts of dark matter [18].

Another source of observational evidence for the existence of dark matter comes from gravitational lensing, which does not rely on orbital dynamics but rather uses the effects of general relativity to predict the mass. The results obtained for the mass-to-light ratio are in agreement with those obtained from dynamical studies [19].

Further evidence for the existence of dark matter comes from Big Bang nucleosynthesis, structure formation studies, and investigations of the anisotropies in the Cosmic Microwave Background, especially those by COBE, Boomerang, and WMAP [20-23]. The WMAP power spectrum results for the Cosmic Microwave Background provided compelling evidence for the existence of dark matter. The first peak in the power spectrum is related to baryonic matter, whereas the third peak, which was resolved by WMAP, is directly related to the density of dark matter [24,25].

The above observations succeeded in ruling out certain models for structure formation like cosmic strings, and lent support to other theories like cosmic inflation. WMAP also succeeded in establishing the LCDM model which is currently considered the Standard Model of Cosmology. In this model, the universe is flat and is dominated by dark energy but with appreciable contributions from dark matter [24]. In this so-called concordance model, the total density parameter, W₀, has three contributions:

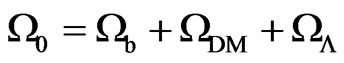(6)

where the observed value for: the baryon density W_b = 0.04; for the dark matter density W_DM = 0.23; and for the dark energy density W_L = 0.73. Of course, for a flat universe, these contributions add up to give a total W₀ = 1.

3. WIMPs as DM Candidates

The interest in WIMPs as dark matter candidates arises from a combination of particle physics, astrophysics, and cosmological arguments. The main astrophysical motivation for WIMPs is the success of cold dark matter theory to explain the origin of galaxies and large scale structure of the Universe [26]. WIMPs, if they exist, are all stable particles. All current theories assume that galaxies and the structure of the Universe arise from the gravitational growth of density fluctuations. As mentioned earlier, these assumptions were verified by the Cosmic Background Explorer satellite (COBE), and more recently by the Wilkinson Microwave Anisotropy Probe (WMAP). The cosmological motivation for WIMPs is that their mass could be adjusted to give an W_DM that could even reach 1, something that has been referred to as the WIMP miracle. It requires a WIMP having a mass of the order of 10 GeV and an asymmetry equal to the baryon asymmetry [27]. WIMPs interact only through the gravitational and weak forces, and therefore they are considered as the primary candidates for dark matter.

3.1. Axions

Many hypothetical particles have been proposed as dark matter candidates. Among these is a hypothetical elementary particle called the axion that was first postulated in 1977 to resolve the strong CP (charge conjugation and parity) problem in quantum chromodynamics. Axions were considered as a potential candidate for cold dark matter. They have no electric charge, a very small mass, and an interaction cross section for both the strong and weak nuclear forces. Therefore, they interact only weakly with ordinary matter [28]. The axion mass is given by (see for example [29])

(7)

where m_u » 4 MeV and m_d = 8 MeV are the up and down quark masses, respectively, and m_p = 135 MeV is the pion mass, f_a is the axion decay constant, and f_p » 93 MeV is the pion decay constant. Astrophysical constraints require that f_a ³ 10⁹ GeV, implying an axion mass m_a ≤ 10 MeV [30]. Axion theories predict that the universe would be filled with Bose-Einstein condensates of primordial axions, and thus plausibly explain the dark matter problem [31]. In 2005, it was thought that the PVLAS dark matter detector had received a signal due to axions. However, it was shown later that the PVLAS result was incorrect [32]. In 2009 some authors casted doubt on the existence of axions, arguing that cosmological observations imply that axions create a greater fine tuning problem than the one they are hypothesized to solve [33].

3.2. Cosmions

Another particle that was of interest three decades ago is the cosmion. It was proposed to solve the solar neutrino problem [34]. This particle acts as an efficient transporter of heat in the Sun’s core and thereby reduces the emission rate of ⁸B neutrinos. In order for the cosmion solution to work, its mass must be in the range of 4 ≤ m_d ≤ 10 GeV [27]. It is clear that the relatively recent discovery of neutrino oscillations in the Sudbury Neutrino Observatory provides a natural way to explain the solar neutrino problem [35,36].

3.3. Supersymmetric Particles

Supersymmetric models provide a whole set of possible particles as DM candidates. Some supersymmetric particles were introduced by particle theories to solve problems entirely unrelated to the cosmology of dark matter. Among these is the lightest supersymmetric particle (LSP) which is a stable particle in models with R-parity conservation. If LSP exists, it may account for the observed missing mass of the Universe. In order to fit observations, LSP must be neutral, non-colored [37], interacts only through weak and gravitational interactions, and must have a mass of 100 GeV to 1 TeV. With these constraints, theoretical studies limit the LSP to either the gravitino, the sneutrino, or the neutralino, a mixture of neutral Majorana fermions, namely, the photino, the higgsino, and the zino [38,39]. In what follows, each of these particles will be discussed separately as a potential DM candidate.

3.3.1. Gravitino

The gravitino is the supersymmetric partner of the graviton. It has a spin of 3/2, and is not a WIMP. If it exists, it is the fermion mediating supergravity interactions. According to the Standard Model, the mass of the graviton must not exceed 1 TeV/c² [40]. The gravitino has a mass

(8)

where F is the supersymmetry-breaking scale squaredand 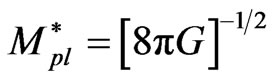» 2.4 × 10¹⁸ GeV. The gauge hierarchy problem requires that F» (10¹¹ GeV)², and therefore all the superpartners including the gravitino have a weak-scale mass [29]. Two possible options emerge from the stability status of the gravitino. In the first option, the gravitino is a stable dark matter candidate that obeys the R-parity conservation. In such a case, gravitinos would have been created in the very early universe. It turns out that the calculated density of stable gravitinos is much higher than the observed dark matter density [41]. The second option is that the gravitino is unstable. In this case, it will decay only through gravitational interaction with a lifetime of the order of, without contributing to the observed dark matter density. In the above relation, M_pl = hc/G = 1.2 × 10¹⁹ GeV is the Planck mass, and m is the mass of the gravitino. Assuming m is of the order of TeV, would imply a lifetime of the order of 10⁵ seconds, which goes well beyond the era of nucleosynthesis. The decay products of the gravitino may destroy almost all nuclei created in this era, which is inconsistent with observations [42]. Other possible solutions to the cosmological gravitino problem include the split supersymmetry model where the gravitino mass far exceeds the TeV scale, or models in which the R-parity is violated, which would preclude the synthesis of primordial nuclei [43].

3.3.2. Sneutrino

Another dark matter particle that is of interest is the sneutrino. According to the Minimal Supersymmetric Standard Model (MSSM), the sneurtino is ruled out as a DM particle, because it exhibits large scattering and annihilation cross sections. Its abundance is limited and it shows null results in direct detection experiments for all masses near m_weak » 10 GeV - 1 TeV [44,45]. The sneutrino interacts via Z boson exchange and would have been detected by now had it existed. However, extended modules involving right-handed (RH) sneutrinos reopen the possibility of the sneutrino as a DM particle [46,47].

3.3.3. Neutralino

The most interesting supersymmetric DM particle is the neutralino. It is a hypothetical WIMP dark matter particle that is predicted by supersymmetry [48,49]. The superpartners of the Z-boson (zino), the photon (photino), and the neutral Higgs (higgsino) have the same quantum number, and therefore they can mix to form four eigenstates of the mass operator called the neutralino. The properties of each neutralino are determined by the details of the mixing, and they would have weak scale masses in the range 100 GeV to 1 TeV. The neutralino is stable in models where R-parity is conserved, and the lightest of the four neutralinos is the LSP. The lightest neutralino is considered as a prime candidate for cold dark matter in the Universe. Neutralino DM particles can be detected by observing gamma rays and neutrinos resulting from their annihilation, preferably in regions of high DM density such as the galactic centers. So far, no experimental evidence of neutralino annihilation has been found.

3.4. Sterile Neutrino

In contrast to fermion masses described in quantum field theories that have terms that couple left-and right-handed fields together, no right-handed neutrino field is predicted by the Standard Model (SM). So all observed neutrinos exhibit left-handed helicities, where spins are antiparallel to momenta. Furthermore, all antineutrinos have left-handed helicities. Therefore, all neutrinos and antineutrinos are massless. Adding a right-handed neutrino may give them mass through the same mechanism that generates mass for quarks and charged leptons. This is achieved by adding a Majarona mass term to the Lagrangian, and thus extending the SM model to include more than two sterile neutrinos. When electroweak symmetry is broken, mass eigenstates will consist primarily of a combination of left-handed neutrinos called active neutrinos, whereas those dominated by right-handed neutrinos are called sterile neutrinos (n_s). Sterile neutrinos do not interact via any fundamental interaction of the SM except for gravity. In general, they are not considered DM candidates. However, there exists a range for the Yukawa coupling in the SM where sterile neutrinos may be dark matter candidates. The mixing angle in this case is defined by

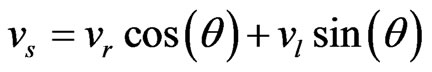(9)

where n_r and n_l are a linear combination of right-handed and left-handed gauge eigenstates, repectively. All the mechanisms of production of sterile neutrinos require very small masses and mixing angles to be viable candidates for DM [29]. Sterile neutrinos can be produced by oscillations at temperatures T » 100 MeV [50]. Being neutral particles, sterile neutrinos do not interact electromagnetically, weakly, or strongly with known particles, and therefore they are very difficult to detect. Because of their mass, however, they interact gravitationally, and they are heavy enough to explain cold dark matter.

3.5. SuperWIMPs

SuperWIMPs are superweak interacting massive particles that have the required relic density, but their interaction is much weaker than the weak interaction. In spite of their superweak interaction, superWIMPs scenarios correctly predict signals emanating from cosmic rays. In the early Universe, one scenario assumes that WIMPs freeze out but later decay to produce superWIMPs that form the dark matter that exists today. Because superWIMPs are very weakly interacting, they will not affect the WIMPs’ freeze out in the early Universe. This causes the WIMPs to decouple with a relic density W_WIMP = W_DM. SuperWIMPs inherit their relic density from WIMPs and therefore produce the required DM density. If superWIMPs interact only gravitationally, the natural time scale for WIMPs to decay to superWIMPs is (1/Gm³_weak) » 10³ to 10⁷ seconds [29]. Superwimps may also be produced after reheating, in the era where the inflation potential is transferred to SM particles. If the temperature is high enough, significant amounts of superWIMPs are generated [51-53]. The superWIMP relic number density is linearly proportional to the reheating temperature T_R, with the constant of proportionality equal to the gravitino production cross section [29]. For a gravitino mass m_gravitino ≤ 100 GeV, the constraint on W_DM implies T_R ≤ 10¹⁰ GeV [54]. Thus, the gravitino is a typical superWIMP particle [55,56].

Another example of a superWIMP is the axino [57,58]. The axino is the supersymmetric partner of the axion. If both axions and axinos contribute to DM, then this would constitute an interesting multicomponent DM scenario [59]. SuperWimp candidates in the form of KK graviton and axion states also exist in the Universal Extra Dimentions (UED) models [55]. The KK graviton is the lightest KK state for all R^-1 800 GeV, where R is the compactification radius [60]. The lightest stabilized KK states by KK-parity conservation have very similar properties to their supersymmetric counterparts [29]. To sum up, there are many superWIMP candidates that inherit their relic density from WIMPs, and are thus produced with the required relic density.

4. Kaluza-Klein Dark Matter

Extra spatial dimensions provide an alternative to weakscale physics. The possibility of the existence of extra spatial dimensions dates back to the work of Kaluza and Klein in the 1920s. In the Universal Extra Dimensions (UED) model, all particles are restricted to move in a flat and compact extra dimension of size 10^-18 m or smaller. In minimal UED, there is one extra dimension of size R, compactified on a circle. In this model, every SM particle has an infinite number of partner particles with mass nR^-1 at every Kaluza-Klein (KK) level n. These particles have the same spin, in contrast to superpatners. The KK parity in UED models is preserved, implying that the lightest KK particle (LKP) is stable and a possible dark matter candidate [61,62]. The required LKP mass is 600 GeV ≤≤ 1.4 TeV, where is the LKP mass, the level 1 partner of the hypercharge gauge boson, sometimes called the KK photon. The detection of KK dark matter particles can be achieved by elastic scattering via coupling with nuclei through the exchange of Higgs bosons and KK quarks. Indirect detection of KK dark matter has several attractive features. Firstly, almost 60% of KK dark matter annihilates into charged lepton pairs (20% for each generation), 33% of the annihilation produces pairs of up quarks, and 3.6% produces neutrino pairs. The remaining 3.4% generate down quarks and Higgs bosons. Secondly, the low velocity cross section is the maximum possible for a thermal relic. Finally, KK dark matter spin-dependent elastic scattering cross sections for protons can be quite large, making the capture of such particles in the Sun an efficient process, which leads to the production of large neutrino fluxes.

5. Primordial Black Holes and Holeums

Theoretical investigations have shown that black holes may have been formed in the early universe due to initial inhomogeneities [63]. Hawking [64,65] argues that primordial black holes (PBH) were formed in a wide spectrum of masses ranging from 2.17 × 10^-8 kg, corresponding to the Planck mass, up to 10¹⁷ solar masses. Formation of PBH is triggered when the gravitational attraction in certain overdense regions in the early Universe overcomes the pressure forces and the velocity expansion. This condition is realized when the potential energy of self-gravitation exceeds the kinetic energy of expansion. Hawking has shown that quantum effects cause black holes to create and emit particles as if they were blackbodies of temperature

(10)

where h and k_B are the Planck and Boltzmann constants, respectively. As Equation (10) shows, the Hawking temperature, T, is inversely proportional to the black hole mass, M_BH, and thus, as the black hole radiates, its temperature increases. Dimensional arguments indicate that the lifetime will be less than the age of the Universe only if M ≤ 10¹⁵ g [66]. Non-rotating PBH with initial mass 5 × 10¹⁵ g would have just evaporated within the present age of the Universe, whereas a black hole created maximally rotating would have just evaporated if its initial mass was 7 × 10¹⁵ g. If the Big Bang spews PBHs with enough mass, they will be manifested as dark matter. Many models have been proposed to describe the mechanism of evaporation. The Hagedron model assumes that the PBH mass would be converted in an extremely short time to hadronic matter at T_PBH ~ 140 - 160 MeV [67]. In the quark-gluon deconfinement phase transition model, the emitted free quarks and gluons would hadronize at some distance from the PBH horizon at a temperature T ~ 100 - 300 MeV [68]. Diffused gamma rays in the galactic halo may serve as an indicator of the PBH density in the Galactic halo, and thus of dark matter [68,69]. Cline et al. [68] assumed a clumping factor of 5 × 10¹⁵ g corresponding to a density of PBH of 10¹⁰ pc^-3 in the Galactic halo. In this case, they estimated the number of PBHs to be ~10²². For a decay rate of 3 × 10⁴ s^-1, they found a photon flux of ~10³⁸ erg/s released into the halo. Cline [70] further assumed a Page-Hawking bound of 2 × 10⁴ pc^-3 and obtained a diffuse gamma-ray flux of ~0.12 photons m^-2·s^-1·sr^-1. This result is consistent with the value obtained by [71,72]. An important remark concerning the above estimation of the Galactic flux is that the evaporation is restricted to PBHs with masses corresponding to the present epoch.

Detection of PBHs was the subject of intensive research since their existence was postulated in the early 1970s. The Hawking evaporation is the key process that allows a potential detection of PBHs. The evaporation is accomplished by a burst of emitted particles and gamma rays. Thus, the population of the galactic halo with PBHs can be inferred only by a careful analysis of possible signals emanating from their evaporation products. No such signal has been reported so far.

Chavda & Chavda [73] have shown that PBH in the early universe did not decay until gravity decoupled from other interactions. In this case, they demonstrated that micro PBH, having masses between 8 × 10¹⁸ GeV and 10¹⁹ GeV, formed gravitational bound states called holeums when the temperature of the Universe was between 10³⁰ K and 10²⁹ K. Being coupled, these PBH will not evaporate by the Hawking mechanism, unless they are ionized. The condition leading to the formation of stable bound states of PBHs are met when extremely high number density, vastly stronger gravity, and enormously large rates of interaction dominate the fireball. The frequency of the gravitational radiation emitted by a holeum when it makes a transition from a higher state to a lower state n is given by

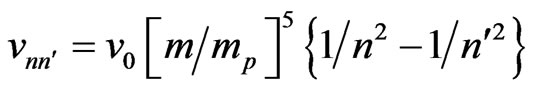(11)

where, n₀ = m_pc²/4h, and m_p is the Planck mass. The energy spectrum given by the above equation is identical to that of the hydrogen atom. In other words, the holeum is a gravitational analog of the hydrogen atom. Chavda & Chavda [73] consider holeums as an essential component of DM that populates the Galactic halo. Holeum theory, in spite of its richness, is still in the infant stage, and a lot of future theoretical and observational work has to be accomplished before testing its adequacy as a DM candidate.

6. Massive Astrophysical Compact Halo Objects

Massive astrophysical compact halo objects (MACHOs) are any kind of astronomical object in the Galactic halo that may account for dark matter. Generally, these bodies emit no light, or in certain cases they may emit very faint radiation in the far infrared region of the spectrum. Therefore, they are very difficult to detect using conventional methods. MACHOs include objects such as black holes, neutron stars, brown dwarfs, or freely floating planets. Detection of MACHOs becomes possible when they pass in front of a star through microlensing [74]. The MACHO gravity amplifies light by gravitational micro-lensing, causing the star to appear brighter. The increase and subsequent decrease of light intensity caused by microlensing has a symmetric form, with no change in wavelength. Two important quantities characterize microlensing. The first is the Einstein angle, also called the Einstein radius, which is given by

(12)

where G once again is the gravitational constant, M is the lens mass, d_L is the distance of the lens, and d_S is the distance of the source. A typical value for the Einstein radius of a bulge microlensing event is 1 milliarcsecond, which is a very small quantity. The second important quantity of a microlenseing event is the amplification factor A, which is given by

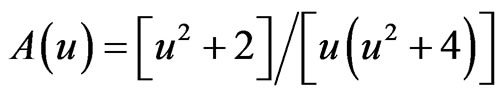(13)

where u is a unitless number defined as the angular separation between the source and the lens. An important property of A(u) is that it is always greater than 1, and therefore microlensing can only increase the brightness of the source. As u approaches infinity, A(u) approaches 1, that is, at large separations microlensing becomes negligible. Finally, for perfect alignment (u = 0), A(u) becomes infinite.

Certain theories postulate the existence of PBHs or holeums surrounding our galaxy. The black holes can be detected by observing possible bright gas, or an accretion disk formed by the pulling of nearby gas. Alternatively, they can be identified by a burst of gamma rays and particles resulting from their evaporation. However, there is no evidence so far of a microlensing event by a PBH. Neutron stars and old white dwarfs may radiate away enough energy to become cold and therefore undetectable. Nevertheless, the Universe is not old enough for these objects to reach this stage of evolution. Brown dwarfs are “aborted stars” and emit very faint infrared radiation, basically from their gravitational contraction.

Gravitational microlensing has inspired many groups to look for MACHOs in the Galactic halo. One group (MACHO group) claimed that it observed microlensing events accounting for up to 20% of dark matter in the Galaxy with an optical depth toward the Large Magellanic Cloud (LMC) of 1.2 × 10^-7 and toward the Galactic bulge of 2.43 × 10^-6 [8]. The EROS2 collaboration operates with higher sensitivity by a factor of 2, but has not confirmed the results of the MACHO group. The NICMOS instrument aboard the Hubble Space Telescope showed that less than one percent of the Galactic halo mass is composed of red dwarfs [75,76]. Microlensing was also used to discover exoplanets [77-80]. Microlensing has been a powerful tool for discovering planet size bodies. However, the bulk of the discovered events falls way short of accounting for the Galactic DM.

7. Modified Newtonian Dynamics

Modified Newtonian Dynamics (MOND) is a theory that was put forward by Milgrom [81,82] to modify Newton’s law of gravity in order to explain the galactic rotation problem without evoking the need for dark matter. MOND assumes that acceleration is not linearly proportional to the gravitational force at small values. Stars in their journey around the galaxy are assumed to be governed solely by gravitational forces, and therefore, objects in the outer edges of the galactic disk are supposed to have much lower orbital velocities than those close to the center. However, observations reveal that stars at all distances from the center exhibit almost the same speed. Therefore, the rotation curve flattens and extends to much higher distances than the furthest observed visible matter at the edge of the Galaxy. This behavior is usually attributed to the existence of dark matter in the Galactic halo. The same phenomenon is observed in all galaxies. MOND assumes that acceleration due to gravity does not simply depend upon the mass m, but rather on a quantity of the form m/m(a/a_o), where m is some function approaching unity for a large argument, and approaching (a/a_o) for a small argument, where a is the acceleration due to gravity, and a_o is a natural constant equal to 10^-10 m/s². In our everyday world (a/a_o) = 1, and therefore, the change in Newton’s law of gravity is negligible. Applying the above concepts to a star orbiting the Galactic center, one can easily obtain an expression for the orbital velocity

(14)

The above equation predicts that the velocity of a star in a circular orbit far away from the Galactic center is constant, and is independent of its distance from the center. If a and M are known, the constant a_o can be calculated. For our Galaxy [81] found 1.2 × 10^-10 m/s². This is an extremely small quantity, and [81] interpreted this constant as the acceleration that will take an object from rest to the speed of light in the lifetime of the Universe. Many interpretations and inconsistencies have been advanced to discuss the validity of MOND. One interpretation is that the behavior of dark matter in the Galaxy dictates the results of MOND, and in this case DM is tightly correlated with visible matter according to a fixed relation. Compatibility issues between MOND and the observed world have been proposed. It has been argued that acceleration is not the only parameter to be considered. To verify MOND, one may consider large systems, such as galaxies or galaxy clusters, that possess the required dynamics to permit comparison with observation. In this case, MOND agrees with observation within the uncertainties of the data. To test the validity of MOND, experiments should be conducted only outside the Solar System. One proposed experiment involves flying the future LISA pathfinder spacecraft through the Earth-Sun saddle point. MOND was also successful in predicting rotation curves for the majority of low surface brightness galaxies (LSB) [83]. Smolin et al. [84] were unsuccessful in establishing a theoretical basis for MOND from quantum gravity. Recently, a study of a gravity-induced redshift of galactic clusters strongly supported general relativity, but was inconsistent with MOND [85]. In 2006, criticism of MOND based on the Bullet Cluster system was advanced. This is a system of two colliding clusters, and whenever a phenomenon associated with either MOND theory or DM is present, they appear to emanate from a physical location that has the same center of gravity. However, the effect produced by DM in this colliding system appears to emanate from different points in space and not just from the center of mass of the visible part in the system. This is easy to discern due to the higher energy collisions of the gas in the vicinity of the colliding galactic clusters [13]. This observation cannot be explained by a purely baryonic model. To sum up, MOND was not able to address all issues raised by observations. Tensor-Vector-Scalar (TeVeS) gravity theory is a relativistic theory proposed as an equivalent to MOND [86]. This theory was able to explain structure formation without cold dark matter, but required ~2 eV massive neutrinos. However, other authors claim that TeVeS cannot explain Cosmic Microwave Background anisotropies and structure formation at the same time. Another theory known as nonsymmetric gravitation theory was proposed to explain the rotation curves of galaxies [87]. However it was unable to address other issues associated with dark matter. Furthermore, conformal gravity theory claims to offer an alternative explanation to DM [88].

8. Supersymmetry, Superstrings, and Dark Matter

Supersymmetry is one of the great achievements of particle physics. It is regarded as a necessary feature of quantum theories of gravity. It is derived from the idea that there should be a fundamental symmetry in nature between fermions and bosons.

In supersymmetry, there is one superpartner particle state for every ordinary state. In a previous section we discussed the possibility that LSP constitutes potential candidates for DM. It is believed that these particles have not yet been observed because supersymmetry is a broken symmetry, and consequently the superpartners are heavier than the known elementary particles. Several arguments have been presented to estimate the range of a typical superpartner mass. It is argued that a range of the order of 100 GeV to 1000 GeV is consistent with electroweak symmetry breaking and with the unification of the electroweak and strong nuclear forces.

The prospect of detecting superpartners relies to a great extent on accelerators capable of achieving such high energies. The Large Hadron Collider (LHC) is designed to reach energies exceeding the above limit. Therefore, if supersymmetry is correct, physicists have good reasons to believe that LHC can find the new spectrum of predicted particles. Nevertheless, not finding superpartners in future experiments does not rule out their existence, since there is no compelling evidence that they necessarily evolve in our spacetime dimensions.

The last few decades have witnessed the emergence of superstring theory as the leading candidate for a unified description of fundamental particles and forces in nature including gravity. In this theory, particles arise as excitations of strings and interactions are simply given by the geometric splitting and joining of these strings. There are five kinds of superstring theories, but recent developments have shown that what was thought to be a set of completely different theories is in fact a different way of looking at the same thing. The unified string theory is called the M theory. Among the superstring theories is a symmetry group known as E₈ × E₈ Heterotic string theory that was historically thought to be the most promising theory describing the physics beyond the Standard Model. It was discovered in 1987 by Gross, Harvey, Martinec, and Rohm [89]. For a long time it was thought to be the only string theory relevant to our Universe. The symmetry group E₈ × E₈ essentially describes two universes living alongside each other. Each of the E₈ symmetries can be naturally broken and reduced to the kind of symmetries used in particle physics to describe the Universe. So, only one E₈ component is needed to describe our Universe, leaving a complete duplicate set of possibilities. The symmetry between the two halves of the group was broken at the Planck era when gravity split away from the other forces in nature. Some theorists interpret the E₈ × E₈ group in terms of two interpenetrating universes but influencing each other only through gravity. A speculative idea is that the other world is a shadow universe and is identified with dark matter. An interesting perspective would be to investigate the possibility that the E₈ component represents a “supersymmetric universe”, a world populated by supersymmetric particles, and remains bound to our Universe through gravitational interaction. Although this idea is speculative at this stage, it provides a frame that accommodates most of the observed properties of dark matter and is supported at the same time by recent theoretical works as explained below. Such developments may preclude our particle accelerators from discovering supersymmetric particles by conventional methods, and the signatures of missing energies may provide an indirect test of their existence.

The strength of the E₈ × E₈ symmetry group comes from the fact that it gives a natural explanation for the origin of DM, while bypassing some unnecessary details that are typically required by any theory concerned with the origin and evolution of the Universe. Among these details are the scenario of inflation and the discrepancy between Ω₀ = 1, as imposed by inflation, and Ω₀ = 0.2, as obtained from primordial nucleosynthesis. However, in the recent past [14] analyzed old published data of 160 distant galaxies and reported a systematic rotation of the plane of polarization over cosmological distances. The discovery could mean that light travels at two slightly different speeds depending on the direction of movement, or it could mean that the Big Bang spewed two universes, each with an opposite twist.

Another important development was provided by [15]. He introduced a model in which two weakly coupled systems maintain opposite running thermodynamic arrows of time, and concluded that there exists a real possibility that at some distance from us there are regions that exhibit such peculiar directions for the arrow of time. He argued that the extended absorber theory indicates that we would see them (the other universe) at an era later than our own due to the light travel time to them. Moreover, [15] discussed the way these regions have arisen, and considered the possibility that our Universe will have a Big Crunch in the (our) future. Furthermore, [15] showed that these regions cannot communicate electromagnetically, and he identified the properties of their content with that attributed to dark matter. The analysis of the observational data presented by [14] suggests the existence of another universe. On the other hand, Schulman’s [15] theoretical work indicates the existence of a DM universe evolving in different spacetime dimensions. Accepting these results at face value, we conclude that they are in agreement with the general features of the E₈ × E₈ superstring theory.

Recently, an international team of astrophysicists presented a map of the distribution of dark matter in the Universe [90]. The map was constructed using gravitational lensing data. This result constituted direct evidence for the existence of dark matter. It was shown that DM forms along filaments that span hundreds of millions of light years. These filaments cross each other forming nodes of higher density DM. The most important aspect of these results is that DM tends to clump and form large scale structures similar to those observed for the distribution of visible matter in the Universe. This view supports the E₈ × E₈ Heterotic string theory in providing insight into the spacetime manifold of dark matter.

9. Conclusions

Dark matter has been one of the most challenging topics in cosmology for the past 80 years, both for observers and theoreticians. In this paper, we have highlighted the difficulties associated with the current detection strategy, which is primarily based on incomplete theoretical models. A wide spectrum of particles has been proposed as DM candidates. In spite of the ever growing sophistication of the detection techniques, none of the proposed DM particles has been discovered so far. The Large Hadron Collider (LHC) will certainly be the right machine to determine the road map for identifying the valid theoretical models in particle physics, which in turn will have a great impact on future search strategies. The recent discovery of the Higgs boson has provided new momentum for the Standard Model as a cornerstone in our understanding of the Universe. Although energies of supersymmetric particles fall in the detection range of LHC, a failure to discover any of them does not necessarily disprove their existence, but will rather raise questions about their nature and the strategy to be adopted to discover them, or alternatively may motivate scientists to embark on new physics.

MACHO searches, on the other hand, have not been conclusive in accounting for the missing mass. Furthermore, accepting PBH and holeums as potential candidates for DM is premature at this stage, since no signal from their potential evaporation has been received despite intensive searches. However, their existence may in the future be indirectly inferred through other strategic searches, such as the intensity of the Galactic gamma ray background, which is an important component of their evaporation products.

It was shown that the E₈ × E₈ Heterotic string theory offers a general framework to understand the nature of DM. It seems to be consistent with certain experimental data [14] and theoretical models [15] that suggested the possibility that DM may evolve in another spacetime manifold. This result conforms to Kaluza-Klein theory, where extra dimensions are needed to accommodate the KK particles. Furthermore, it was pointed out that dark matter surveys, using microlensing techniques, indicate the existence of a large scale structure of dark matter, similar to the distribution of ordinary matter populating the visible Universe.

The essence of the dark matter problem is that it is interdisciplinary in nature, and thus requires a search strategy that utilizes more than one approach. Dark matter will certainly remain a challenge for theoreticians and observers for some time to come.

REFERENCES

NOTES

^*Corresponding author.