Journal of Modern Physics
Vol. 2 No. 8 (2011) , Article ID: 6716 , 9 pages DOI:10.4236/jmp.2011.28094
Cosmic Transmutation Conjecture
Colina de los Chopos, Instituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, Madrid, Spain
E-mail: {lbabsail, leda, salwam, smasuda}@KSU.EDU.SA
Received January 5, 2011; revised March 2, 2011; accepted April 5, 2011
Keywords: Big Trip, Multiverse, Boltzmann Brains, Transmutation
ABSTRACT
This paper analyzes the big trip phenomenon, restricting it to happen only in the context of the multiverse when the involved wormhole is asymptotically flat and recent criticisms are pointless. A new kind of Lorentzian asymptotically anti-de Sitter wormholes is considered in some detail and it is seen that such wormholes cannot contribute the big trip phenomenon. The ideas of big trip, multiverse and Boltzmann brains are then used to advance the conjecture of cosmic transmutation according to which the host universe where one of the mouths of a grown up wormhole is inserted may be converted into a universe similar to the traveling one if the latter contains a civilization which is typical also in the host universe. The origin of life in the context of the multiverse is then briefly discussed.
1. Introduction
In the late 1990s astrophysicists discovered [1-5] that the expansion of the universe is accelerating, rather than slowing down as most had expected, so creating the cosmic framework where new ideas and phenomena like dark and phantom energy, multiverse and even Boltzmann brains could most comfortably accommodate. Most cosmologists think that the big rip singularity that arises if the universe is endowed with phantom energy is an end of time, that there is no point in trying to figure out what is going on after that singularity [6]. Simply they say the big rip marks a doomsday, the end of the universe, and nothing can be expected to happen later; that even it does make no sense to wonder on that. The main argument supporting that attitude comes about from the feature that the classical laws of sciences all fail to hold at a singularity [7], and therefore if this is cut out then the whole manifold is divided into two disconnected parts which can by no way be continued into each other. Thus, if the vacuum of the universe is dominated by phantom energy [8], then the universe will certainly have an end at the big rip singularity. Or it will not? There are in fact two main reasons against this conclusion. First, since as we are approaching the big rip the energy density rises dramatically and becomes infinite at the singularity, the universe must have an essentially quantum behavior [9] at the big rip and the singularity smoothed out by quantum effects. Second, as the singularity is approached all sorts of wormholes would copiously crop up which may connect the regions before and after the big rip [10]. So, the evolution of a phantom universe does not stop at the big rip but continues into a contracting phase which makes the size of the universe to steadily decrease during an infinite future. On the other hand, before reaching the big rip, the phantom universe could undergo a gigantic disruption in its causal evolution, in fact one of the most bizarre phenomena ever considered in cosmology: the big trip [11]. In this paper we show that only wormholes which are asymptotically flat can be involved at the big trip, and that this phenomenon may lead to the novel notion of cosmic transmutation in the context of the multiverse, which we actually conjecture.
2. The Big Trip
The cosmic big trip is a phenomenon that could happen in the far future of the universe by which a microscopic Lorentzian wormhole (living in the space-time foam or not) of a universe dominated by phantom energy suffers a super rapid swelling due to phantom energy accretion that allows the hole to remain quantum-mechanically stable for a while and become even larger than the universe itself, before the big rip singularity is reached [11-14]. Once the wormhole blows up, it destabilizes into a Einstein-Rosen bridge which rapidly loses mass to vanish at the big rip singularity [11] (Figure 1).
The Morris-Thorne wormhole is described by a spacetime which is asymptotically flat, and therefore, during the time interval on which it exceeds the size of the universe their mouths must be necessarily inserted into universes quite larger than the one where the wormhole was originally grown up [12-14]. Thus, for a wormhole in a given phantom universe to undergo a big trip process it appears to be necessary that such a universe belongs to the set of universes making up a multiverse [12-14].
The nature of this phenomenon is rather bizarre and hence it calls for rejection when at first sight considered. However, all the attempts to dismiss it [15,16] have not succeeded so far [12-14]. The last and most remarkable of such attempts by Faraoni raised [17] two main reasons. On the one hand, it pointed out that the phantom energy accretion procedure used to generate a big trip does not take into account the feature that we are not dealing with a vacuum solution. However, all our calculations [18,19] are finally referred to the asymptotic case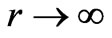 , where the r.h.s. of the Einstein equations for an ansatz
, where the r.h.s. of the Einstein equations for an ansatz 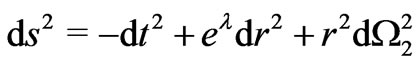 all vanish (see Section 3) for the simplest Morris-Thorne solution [20,21]. It follows that the mathematical procedure followed to get the big trip is correct if the big trip is defined for an asymptotic observer living in the flat region, such as it is actually the case [12-14]. On the other hand, Faraoni also claimed [17] that the accretion of phantom energy with a perfect fluid equation of state
all vanish (see Section 3) for the simplest Morris-Thorne solution [20,21]. It follows that the mathematical procedure followed to get the big trip is correct if the big trip is defined for an asymptotic observer living in the flat region, such as it is actually the case [12-14]. On the other hand, Faraoni also claimed [17] that the accretion of phantom energy with a perfect fluid equation of state 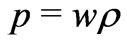 is characterized by a radial velocity
is characterized by a radial velocity  (with
(with  the scale factor) which strictly vanishes at the big rip singularity and in any event quickly decreases with time for
the scale factor) which strictly vanishes at the big rip singularity and in any event quickly decreases with time for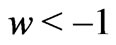 . Thus, also at the time where the big trip would occur, accretion of phantom energy would be largely prevented and the big trip phenomenon would not take place at all. Besides the feature that the size of the wormhole throat equalizes that of the universe before it diverges, what matters here is not the fluid velocity but its flow (as expressed as phantom energy per unit surface per unit time) which can be roughly given by
. Thus, also at the time where the big trip would occur, accretion of phantom energy would be largely prevented and the big trip phenomenon would not take place at all. Besides the feature that the size of the wormhole throat equalizes that of the universe before it diverges, what matters here is not the fluid velocity but its flow (as expressed as phantom energy per unit surface per unit time) which can be roughly given by , that is
, that is , which in fact
, which in fact
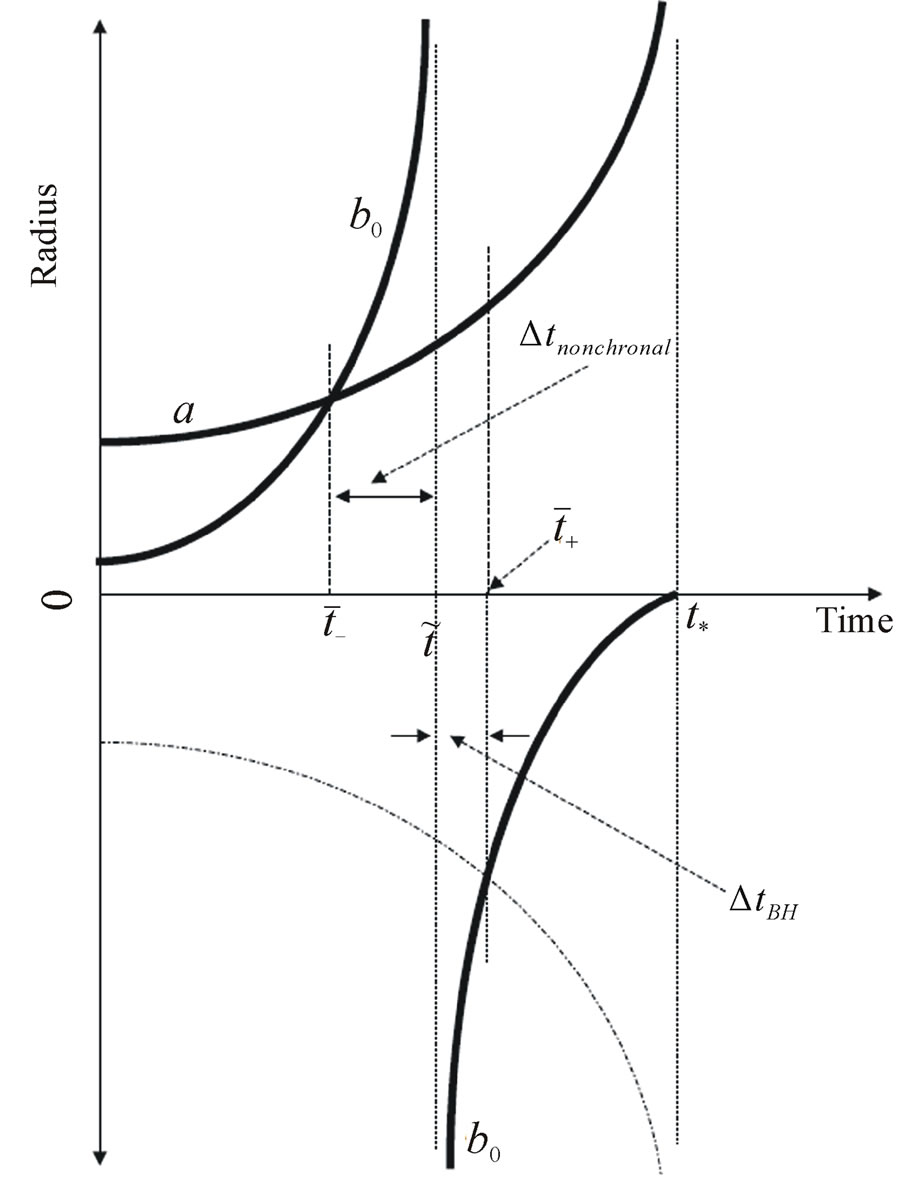
Figure 1. Evolution of the radius of the wormhole throat, 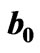 , relative to the scale factor,
, relative to the scale factor, 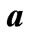 , of the universe, induced by accretion of phantom energy. At a given time
, of the universe, induced by accretion of phantom energy. At a given time  in the future, the negative exotic mass becomes infinite and then changes sign, so converting the wormhole into an Einstein-Rosen bridge whose associated mass decreases down to zero at the big rip at
in the future, the negative exotic mass becomes infinite and then changes sign, so converting the wormhole into an Einstein-Rosen bridge whose associated mass decreases down to zero at the big rip at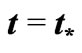 . During the time interval
. During the time interval  there will be a disruption of the causal evolution of the whole universe and there appears the phenomenon of cosmic big trip.
there will be a disruption of the causal evolution of the whole universe and there appears the phenomenon of cosmic big trip.
increases with time and consistently diverges at the big rip [18,19]. Then the argument by Faraoni does not apply to the case and the big trip can not be dismissed, at least due to it (See also the bottom of this section).
It appears that the phenomenon of the cosmic big trip cannot be disregarded if the current and future universe is dominated by phantom energy. Indeed, the key question is whether the latter dominance is actually the case. According to the most recent observational data published [1-5,22,23], the value of the parameter of the equation of state 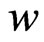 looks to become more and more concentrated around
looks to become more and more concentrated around , with only a weak, decreasing tendency toward smaller values. Although many cosmologists have already concluded therefore that the current universe is dominated by a cosmological constant, it appears that the accuracy and precision of present, and one can foresee that for many years, cosmic technology would not be good enough as for discriminating between a cosmological constant and phantom energy in a crystalclear way. Actually, because a very very tiny difference in the value of
, with only a weak, decreasing tendency toward smaller values. Although many cosmologists have already concluded therefore that the current universe is dominated by a cosmological constant, it appears that the accuracy and precision of present, and one can foresee that for many years, cosmic technology would not be good enough as for discriminating between a cosmological constant and phantom energy in a crystalclear way. Actually, because a very very tiny difference in the value of 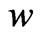 meant completely different qualitative future behavior of the universe on that border and since observational data would always have a strictly nonzero uncertainty, perhaps at least the kind of observations being currently considered would not be the proper deciding argument to settle down the question on the future of the universe, so that both scenarios, and hence the cosmic big trip, had to be simultaneously considered.
meant completely different qualitative future behavior of the universe on that border and since observational data would always have a strictly nonzero uncertainty, perhaps at least the kind of observations being currently considered would not be the proper deciding argument to settle down the question on the future of the universe, so that both scenarios, and hence the cosmic big trip, had to be simultaneously considered.
A possible argument in favor of phantom energy—and hence of the big trip—comes about when one regards  to be a discrete quantity given by [10]
to be a discrete quantity given by [10]
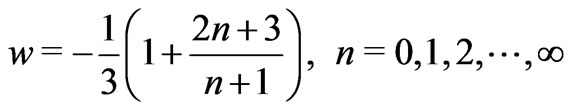
in the interval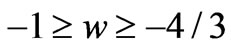 , and as a continuous quantity only in the dark energy regime where the above equation can be still applied, now with
, and as a continuous quantity only in the dark energy regime where the above equation can be still applied, now with  no longer an integer number but continuously varying from
no longer an integer number but continuously varying from  to
to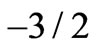 , so covering the whole dark energy continuous interval
, so covering the whole dark energy continuous interval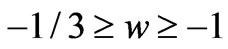 . Clearly, a cosmological constant
. Clearly, a cosmological constant 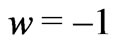 could then be only obtained for strictly
could then be only obtained for strictly , a situation which corresponded to a highly unlikely infinitely excited equation of state which one might only consider to be a sensible choice as the age of the universe tended asymptotically to infinite. Thus, a phantom universe appears to be the most probable choice.
, a situation which corresponded to a highly unlikely infinitely excited equation of state which one might only consider to be a sensible choice as the age of the universe tended asymptotically to infinite. Thus, a phantom universe appears to be the most probable choice.
On the other hand, having a continuous  -spectrum in the dark energy interval and a discrete
-spectrum in the dark energy interval and a discrete  -spectrum for the phantom energy regime seems a logical consequence from the feature that whereas the energy density for dark energy is a decreasing function of the cosmic time, that for phantom energy always increases with cosmic time, reaching values so high that necessarily requires quantization [9]. Around the big rip singularity the phantom energy density becomes of the order of the Planck scale which means that such a singularity should be smoothed out by the associated quantum effects, so the evolution of the universe should continue beyond that point. For this to be mathematically consistent so that the scale factor is real and positive after the big rip time, the discrete (quantized) character implied by the above formula would precisely be the required condition.
-spectrum for the phantom energy regime seems a logical consequence from the feature that whereas the energy density for dark energy is a decreasing function of the cosmic time, that for phantom energy always increases with cosmic time, reaching values so high that necessarily requires quantization [9]. Around the big rip singularity the phantom energy density becomes of the order of the Planck scale which means that such a singularity should be smoothed out by the associated quantum effects, so the evolution of the universe should continue beyond that point. For this to be mathematically consistent so that the scale factor is real and positive after the big rip time, the discrete (quantized) character implied by the above formula would precisely be the required condition.
It is worth noticing that a similar argument can also be applied to the big trip phenomenon. Even though the nature of the wormhole would likely keep being essentially classical at the moment that its throat radius equalizes that of the universe, when the throat size approaches infinity then the exotic energy density would tend to infinite as well. A quantization of the wormhole size appears to be then required leading probably to maximum finite, though very large, size for the throat. Whether such a quantization stabilizes the wormhole or not is a question which requires further investigation. In any event, once it becomes a Einstein-Rosen bridge [12-14,24], the wormhole pinches off by the throat and the resulting black and white holes would later disappear by phantom energy accretion.
The big trip scenario is rather appealing even though references [15-17] want to disprove it. The arguments in these references have been however refuted in reference [12-14] and mainly reference [18,19]. One always can write a solution to the Einstein equations showing the big trip phenomenon provided we start with a non static metric using as matter phantom energy, and (see Section 3) no cosmological term, neither positive nor negative, is included. If, on the other hand, we assume an ad hoc wormhole solution displaying big trip, one can show that there are two cases in which the chronology horizons are quantum mechanically stable and therefore violate the chronology protection conjecture. In fact, in terms of the Rindler coordinates the metric of the wormhole becomes
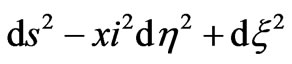 , by introducing the definitions
, by introducing the definitions
 ,
,  which covers the quadrant
which covers the quadrant , and plus the reflection
, and plus the reflection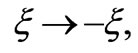 describing the region
describing the region . Identifying the Misner-symmetric points we can derive the Two-point Hadamard function, and hence the regularized energy-momentum tensor which becomes proportional to
. Identifying the Misner-symmetric points we can derive the Two-point Hadamard function, and hence the regularized energy-momentum tensor which becomes proportional to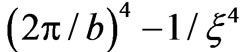 . This tensor diverges as one approaches the chronology horizon
. This tensor diverges as one approaches the chronology horizon , except para a conformal vacuum
, except para a conformal vacuum 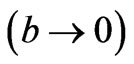 or the instability is delayed beyond the big trip time when the wormhole accretes phantom energy [18,19].
or the instability is delayed beyond the big trip time when the wormhole accretes phantom energy [18,19].
3. Asymptotically Anti-De Sitter Morris-Thorne Wormhole: A Simple Example
For the simplest ansatz that corresponds to a static, spherically-symmetric wormhole spacetime with vanishing shift function,
 (1)
(1)
(where  is the metric on the unit two-sphere) the Einstein equations can be written in the form
is the metric on the unit two-sphere) the Einstein equations can be written in the form


 (2)
(2)
where the prime denotes derivative with respect to the radial coordinate. We can then derive the Lorentzian spacetime metric of the simplest Morris-Thorne wormhole, i.e.
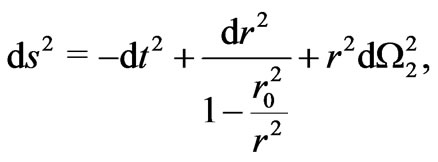 (3)
(3)
with 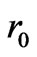 the radius of the spherical throat, if we use the following mixed components of the energy-mentum tensor for matter
the radius of the spherical throat, if we use the following mixed components of the energy-mentum tensor for matter
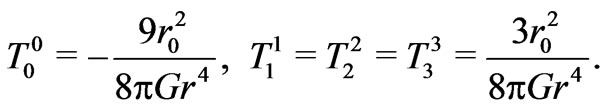 (4)
(4)
Using expressions (4) and the Einstein Equation (2) supplemented with an extra positive cosmological constant term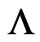 , one can finally obtain the simplest metric corresponding to the topology of a zero-shift function wormhole embedded into a de Sitter space to be
, one can finally obtain the simplest metric corresponding to the topology of a zero-shift function wormhole embedded into a de Sitter space to be
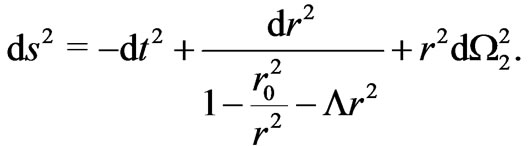 (5)
(5)
Now, if , the usual event horizon of the de Sitter space at
, the usual event horizon of the de Sitter space at 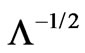 splits into two event horizons at smaller proper distance, placed at
splits into two event horizons at smaller proper distance, placed at
 (6)
(6)
Clearly, metric (5) does not describe the space-time of a wormhole but just that of a given cosmological space which contains a Morris-Thorne wormhole [20,21] whose throat radius is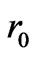 . A proper wormhole metric can still be obtained however for negative cosmological constant. If we insist in having a generalized zero shift function, that space-time corresponded to an asymptotically anti-de Sitter Morris-Thorne wormhole with line element
. A proper wormhole metric can still be obtained however for negative cosmological constant. If we insist in having a generalized zero shift function, that space-time corresponded to an asymptotically anti-de Sitter Morris-Thorne wormhole with line element
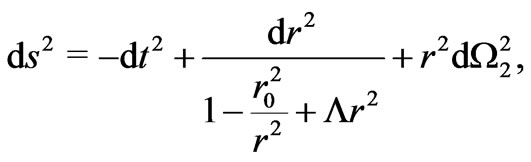 (7)
(7)
where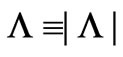 , were it not for the ever-flat
, were it not for the ever-flat 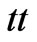 metric component. To a such
metric component. To a such 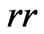 -asymptotically anti-de Sitter space-time we shall continue just denoting as an asymptotically anti-de Sitter Morris-Thorne wormhole for the sake of simplicity. Metric (7) still shows an apparent event horizon at
-asymptotically anti-de Sitter space-time we shall continue just denoting as an asymptotically anti-de Sitter Morris-Thorne wormhole for the sake of simplicity. Metric (7) still shows an apparent event horizon at
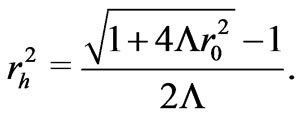 (8)
(8)
That the space-time (7) describes a wormhole with a throat at 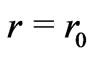 can be checked by (i) re-writing metric (7) in the form
can be checked by (i) re-writing metric (7) in the form
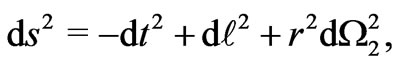 (9)
(9)
where

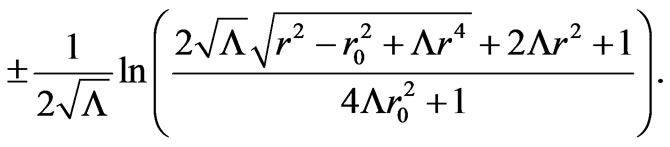 (10)
(10)
It is easy to see now that the parameter  goes from
goes from  (when
(when ) to zero (at
) to zero (at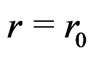 ) and then to
) and then to 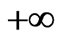 (where
(where  again), such as it is expected for a wormhole with a throat at
again), such as it is expected for a wormhole with a throat at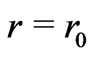 .
.
On the other hand (ii), let us consider a three-geometry at 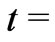 const. respecting spherical symmetry and
const. respecting spherical symmetry and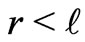 . For, it suffice choosing the slice
. For, it suffice choosing the slice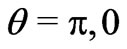 , so that
, so that
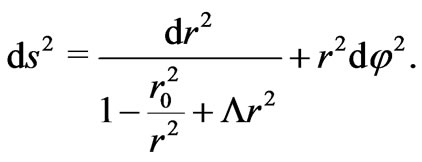 (11)
(11)
We wish now visualize the slice (11) as removed from metric (9) and embedded in three-dimensional Euclidean space which can be described by cylindrically symmetric coordinates 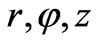
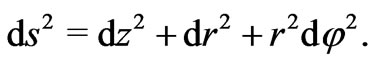 (12)
(12)
The embedding surface is describable by a function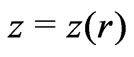 , Thus,
, Thus,
 (13)
(13)
Metric (13) will be the same as metric (11) if we identify the coordinates 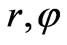 of the embedding space with those of the wormhole and we require the function
of the embedding space with those of the wormhole and we require the function 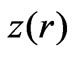 to satisfy
to satisfy
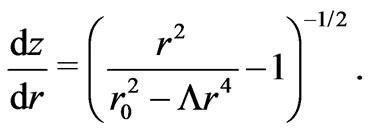 (14)
(14)
Now, if we want the wormhole to be connectible to a asymptotically anti-de Sitter space-time, the embedding surface should flare outward at or near the throat [20,21]. This can be mathematically expressed by the condition, which is in fact satisfied as it can be checked from Equation (14), that is
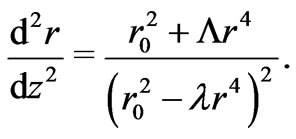 (15)
(15)
Finally (iii) the considered wormhole can be shown to be traversable as a two-sphere surrounding one of its mouths where space-time is nearly anti-de Sitter can be regarded as an outer trapped surface to an observer looking through the wormhole from the other mouth.
However, even though the asymptotically anti-de Sitter wormhole can be converted into a time machine with line element
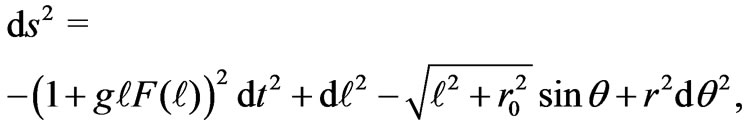 (16)
(16)
(where we have assumed the right mouth to move with relative velocity 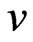 with respect to the left one, so inducing time travel to be allowed,
with respect to the left one, so inducing time travel to be allowed, 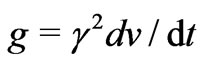 is the acceleration of the moving mouth,
is the acceleration of the moving mouth, 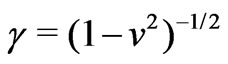 , and
, and 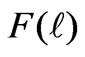 is form factor vanishing on the left half (
is form factor vanishing on the left half (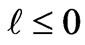 ) of the wormhole and increases monotonously from 0 to 1 as one moves rightward from the throat to the right mouth), and its metric can be maximally extended to smooth out its apparent singularity at
) of the wormhole and increases monotonously from 0 to 1 as one moves rightward from the throat to the right mouth), and its metric can be maximally extended to smooth out its apparent singularity at 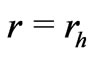 (Figure 2),
(Figure 2),
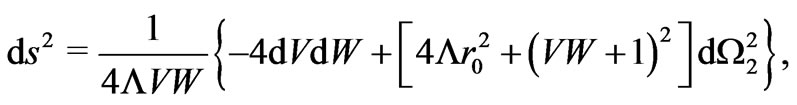 (17)
(17)
(with
 ,
,  where
where
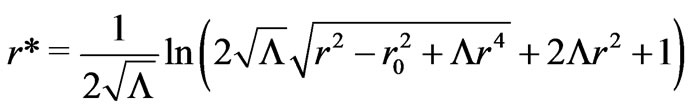
and
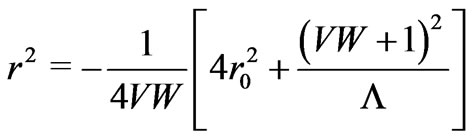 ),
),

Figure 2. Kruskal diagram of the 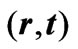 surfaces of the maximally extended space-time of the asymptotically anti-de Sitter Thorne wormhole. Here the new coordinates
surfaces of the maximally extended space-time of the asymptotically anti-de Sitter Thorne wormhole. Here the new coordinates 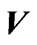 and
and 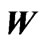 are defined by Equation (17). Null geodesics are at
are defined by Equation (17). Null geodesics are at  degrees to the vertical. The regions where
degrees to the vertical. The regions where 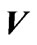 and
and 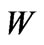 simultaneously have the same sign are forbidden.
simultaneously have the same sign are forbidden.
these wormholes cannot insert their mouths into the asymptotically flat regions of larger universes because of obvious topological reasons. It is for this topological obstruction that the asymptotically anti-de Sitter wormholes cannot enter the big trip phenomenon in a multiverse scenario. Nevertheless, asymptotically anti-de Sitter wormholes can still undergo a swelling process when accreting phantom energy though their throat radius can never exceed the size of the universe where it originally existed. Let us in fact consider the process of dark energy accretion onto one such wormholes. Then, following the procedure put forward elsewhere [11-14,18,19], one can finally derive for the variation rate of the throat radius the expression
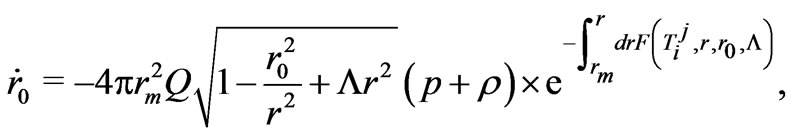 (18)
(18)
where 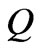 is positive constant,
is positive constant, 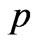 and
and  respectively are the pressure and energy density of dark energy,
respectively are the pressure and energy density of dark energy,  corresponds to the value of the radial coordinate that makes flat the metric,
corresponds to the value of the radial coordinate that makes flat the metric,  is a given function defined in terms of the components of the stressenergy tensor
is a given function defined in terms of the components of the stressenergy tensor 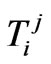 [18,19], and we have used coordinates so that
[18,19], and we have used coordinates so that . Evaluating then this expression at
. Evaluating then this expression at 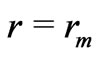 we get the simpler rate
we get the simpler rate
 (19)
(19)
Now, for a general equation of state 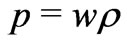 and a simple quintessence field where [25]
and a simple quintessence field where [25]
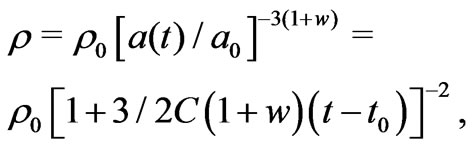 (20)
(20)
with , one may integrate the above rate equation to finally have
, one may integrate the above rate equation to finally have
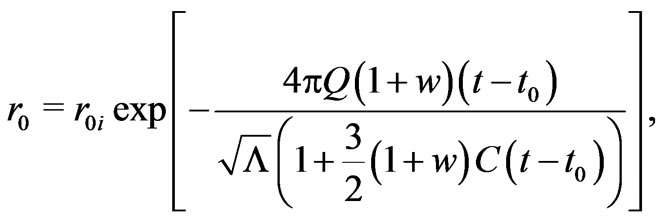 (21)
(21)
with  the initial radius of the wormhole throat.
the initial radius of the wormhole throat.
For dark energy with  we see that the throat radius slowly decreases, tending to a constant radius
we see that the throat radius slowly decreases, tending to a constant radius
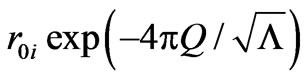 as
as .
.
In the case that the quintessence field behaved like phantom energy,  , the radius of the wormhole throat exponentially increased to reach an infinite value just at the big rip singularity time,
, the radius of the wormhole throat exponentially increased to reach an infinite value just at the big rip singularity time,
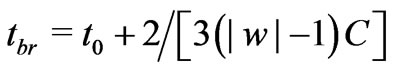
Therefore, an asymptotically anti-de Sitter Lorentzian wormhole does not give rise to the phenomenon of big trip, which requires the wormhole size to blow up before reaching the big rip singularity (Figure 3). Thus, all situations involving a big trip that we are going to consider in what follows requires the presence of wormholes which are asymptotically flat.
4. Cosmic Transmutation in the Multiverse
Generally speaking, there is no relation whatsoever between the spaces and times of two different universes in any models of multiverse [26]. Thus, the relative velocity of the two wormhole mouths inserted into different host universes becomes completely unspecified as they then do the involved time and space traveled by the phantom universe traveling through the wormhole so equipped with a chronology horizon created by such an
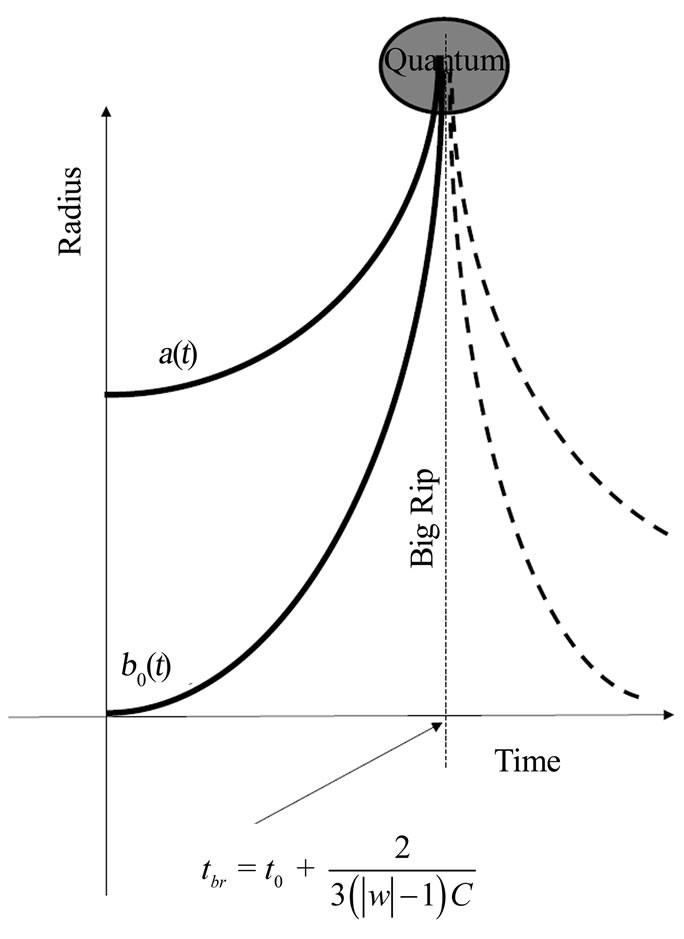
Figure 3. Evolution of the radius of an asymptotically anti-de Sitter wormhole throat, 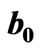 , relative to the scale factor,
, relative to the scale factor, 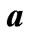 , of a phantom universe, induced by accretion of phantom energy. At time
, of a phantom universe, induced by accretion of phantom energy. At time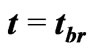 , the negative exotic mass becomes infinite and then starts steadily decreasing while the universe contracts, always keeping a smaller radius than that of the universe. There is no big trip for these wormholes but just an identification of the throat with the universe when this reaches an infinite size. Thus there could be no disruption of the causal evolution of the whole universe. Because the big rip should be dominated by still unknown quantum-gravity effects that presumably prevents the classical singularity, one is tempted to conjecture that at the big rip the universe becomes a quantum universe which is undistinguishable of the throat of a asymptotically anti-de Sitter wormhole.
, the negative exotic mass becomes infinite and then starts steadily decreasing while the universe contracts, always keeping a smaller radius than that of the universe. There is no big trip for these wormholes but just an identification of the throat with the universe when this reaches an infinite size. Thus there could be no disruption of the causal evolution of the whole universe. Because the big rip should be dominated by still unknown quantum-gravity effects that presumably prevents the classical singularity, one is tempted to conjecture that at the big rip the universe becomes a quantum universe which is undistinguishable of the throat of a asymptotically anti-de Sitter wormhole.
unspecified relative motion between the two mouths, a condition that makes it possible the kind of wormhole connection between different universes of the multiverse considered by the big trip.
When a phantom universe swallowed by one of its swelled asymptotically flat wormholes, whose mouths are connected to other, larger universes, ends its big causally-disrupted trip entering one of such larger host universes, it will re-appear in the latter universe in a way which is indistinguishable from a spontaneous fluctuation. If the traveling universe would be endowed with eventual observers, then, relative to the host universe, such observers would behave in a way which would also be fully indistinguishable from Boltzmann brain fluctuations [27-29], and two distinct phenomena could happen, according to how typical are the possible involved civilizations relative to each other.
On the one hand, if the typical observers of the traveling civilization are sub-dominant in number with respect to the observers in the host typical civilization, then its achronal traveling would end with its observers being no longer typical and whatever they might see at the end of their trip is not representative of the host universe at large, keeping the host civilization the role of typical. All that host observers in the host universe would see is the effect of a big spontaneous fluctuation in the spacetime distribution of matter, possibly in the form of a big void disrupting homogeneity [30].
On the other hand, if the typical observers of the traveling civilization vastly outnumbered host typical observers, or if there was no host civilization, the traveling civilization will ultimately become a typical civilization in the host universe and everything that its observers can observe would become representative of a new host universe at large; then the host universe would spontaneously transmute into a new universe having similar characteristics to those of the phantom universe that traveled into it, and that its new typical observers are able to see. It appears rather difficult to know whether or not these observers do realize that they have changed universe. On the other hand, the probability that the visiting observers and those living in the host universe prior to big trip belong all to exactly the same kind, and hence that the transmuted universe be indistinguishable from the previous host universe, can be assumed to be very tiny. This cosmic transmutation is a novel, even more bizarre process which we conjecture here and that ultimately stems from the combined effect of the notions of Boltzmann brains, the participatory principle of Wheeler [31] and the definition of a typical observers and observations [27-29], and could have far-reaching implications in cosmology and even biology.
At first sight, a single cosmic transmutation process leads to a violation of the second law of thermodynamics which in this way would ultimately forbid cosmic transmutation to occur. In fact, the conversion of a pair of universes plus a wormhole into just a single universe would in principle imply a huge reduction of entropy. This would not be the case however if the host universe which vanishes in the transition is a phantom universe. In fact, the thermodynamics of a phantom universe is such that either its entropy is positive and its temperature negative, or vice versa, its temperature is positive and its entropy is negative [32]. In both cases, nevertheless, any process that implied the vanishing of a phantom universe leads to an increase of entropy. Now, the probability that the host universe be a phantom universe appears to be larger than the probability that it be a dark-energy universe or a universe expanding in a decelerated fashion which may undergo a big crunch, simply because the big trip phenomenon occurs quite before the big rip and requires the host universe to be larger than the traveling universe. Of course, host universes could also be non phantom. However, what would matter in the multiverse is not what happens with the entropy of one universe or the set of a few universes, but with the entropy of the whole set of universes entering the multiverse, and it seems that this will always increased on average due to the above argument (See Figure 4), such as the proportion of phantom universes will do due to cosmic transmutation. Nevertheless, the above argument appears to be flawed as far as the second law of thermodynamics requires causal evolution along an arrow of time and a clear distinction between a common future and a common past for the set of all involved universes which, by definition, is by no means possible in the multiverse. It appears then that in order for this question to be settled down once and for all in an unambiguous way one must have a consistent statistical-mechanical description of the multiverse, which by now is far from being actually the case.
5. Summary and Further Comments
We first briefly review the cosmic big trip phenomenon by which accretion of phantom energy by a MorrisThorne Lorentzian wormhole leads that hole to increase size in so a dramatic fashion that its throat eventually exceeds the size of the universe itself even before the big rip is reached. It is shown that such a phenomenon can only take place when the involved wormhole is asymptotically flat. An anti-de Sitter wormhole solution is obtained which is also able to accrete phantom energy but this time in such a way that even though the wormhole throat steadily increases size, it does so just at the rate required for it to follow the expansion of the uni-
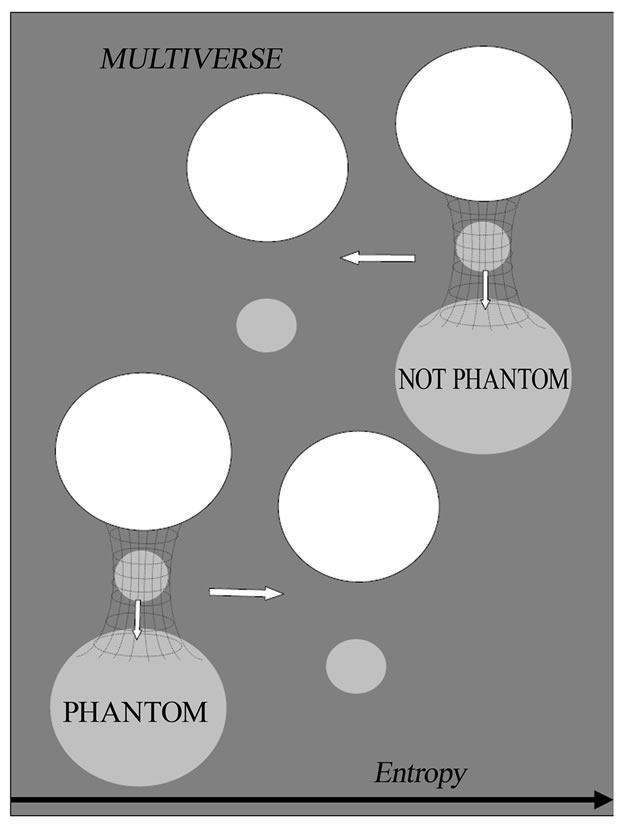
Figure 4. Pictorial representation of a transmutation process which involves: (down) an entropy increase, and (up) an entropy decrease. In the first case the host universe is dominated by phantom energy, 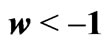 , and in the second one the host universe is dominated by dark energy,
, and in the second one the host universe is dominated by dark energy, 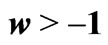 , or is decelerating,
, or is decelerating,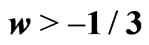 .
.
verse co-movingly, so diverging only at the big rip. A possible explanation for that result might be that the negative cosmological constant entering the asymptotically anti-de Sitter wormhole is essentially quantal in origin, so rendering the cosmic big trip phenomenon to be just an artifact that only appear in the classical limit of the theory. Finally, the ideas of the cosmic big trip, the multiverse and the Boltzmann brains are used in such a daring way as to allow us to advance a cosmic transmutation conjecture according to which the large universe where one mouth of the wormhole that has inflated according to the big trip mechanism is inserted can be transformed in a universe similar to the one that traveled along the wormhole tunnel provided that the latter universe hosted a civilization which becomes typical in the hosting larger universe.
The author thanks Carmen L. Sigüenza for useful comments and discussion. This work was supported by the Spanish MICINN under Research Project No. FIS2008-06332.
REFERENCES
- S. Perlmutter, et al., “Measurements of the Cosmological Parameters Omega and Lambda from the First 7 Supernovae at z >= 0.35,” The Astrophysical Journal, Vol. 483, No. 2, 1997, pp. 565-586;
- S. Perlmutter et al. (The Supernova Cosmology Project), “Discovery of a Supernova Explosion at Half the Age of the Universe and its Cosmological Implications,” Nature, Vol. 391, No. 1, 1998, pp. 51-54;
- P. M. Garnavich, et al., “Constraints on Cosmological Models from Hubble Space Telescope Observations of High Z Supernovae,” Astrophysical Journal Letters, Vol. 493, No. 2, 1998, pp. L53-L57 ;
- B. P. Schmidt, “The Hight Z Supernova Search: Measuring Cosmic Deceleration and Global Curvature of the Universe Using Type Ia Supernovae,” Astrophysical Journal, Vol. 507, No. 11, 1998, pp. 46-63;
- A. G. Riess, et al., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant,” Astronomical Journal, Vol. 116, No. 3, 1998, pp. 1009-1038. doi:10.1086/300499
- R. R. Caldwell, M. Kamionkowski and N. N. Weinberg, “Phantom Energy and Cosmic Doomsday,” Physical Review Letters, Vol. 91, No. 7, 2003, pp. 071301-1-071301-4. doi:10.1103/PhysRevLett.91.071301
- S. Hawking and G. F. R. Ellis, “The Large Scale Structure of Space-Time,” Cambridge University Press, Cambridge, 1973. doi:10.1017/CBO9780511524646
- R. R. Caldwell, “A Phantom Menace?” Physics Letters Vol. B545, No. 1-2, 2002, pp. 23-29.
- S. Nojiri and S. D. Odintsov, “The Final State and Thermodynamics of Dark Energy Universe,” Physical Review, Vol. D70, No. 10, 2004, pp. 03522-1-103522-9.
- P. F. González-Díaz, “Holographic Cosmic Energy, Fundamental Theories and the Future of the Universe,” Gravitation and Cosmology, Vol. 12, No. 1, 2006, pp. 29-36.
- P. F. González-Díaz, “Achronal Cosmic Future,” Physical Review Letters, Vol. 93, No. 7, 2004, pp. 071301-1- 071301-4.
- P. F. González-Díaz, “On the Accretion of Phantom Energy onto Wormholes,” Physics Letters, Vol. B632, No. 1, 2006, pp. 159-161.
- P. F. González-Díaz, “Some Notes on the Big Trip,” Physics Letters Vol. B635, No. 1, 2006, pp. 1-6.
- P. Martín-Moruno, A. L. Marrakchi, S. Robles-Pérez and P. F. González-Díaz, “Dark Energy Accretion onto Black Holes in a Cosmic Scenario,” General Relativity and Gravitation, Vol. 41, No. 12, 2009, pp. 2797-2811. doi:10.1007/s10714-009-0808-8
- V. Faraoni and W. Israel, “Dark Energy, Wormholes, and the Big Rip,” Physical Review, Vol. D71, No. 6, 2005, pp. 064017-1-064017-7.
- A. V. Yurov, V. A. Yurov and S. D. Vereshchagin, “Can we Scape from the Big Rip in the Achronal Cosmic Future?” arXiv: astro-ph/0503433.
- V. Faraoni, “No ‘Big Trip’ for the Universe,” Physics Letters, Vol. B647, No. 5-6, 2007, pp. 309-312.
- P. F. González-Díaz and P. Martín-Moruno, “Wormholes in the Accelerating Universe,” Proceedings of the 11th Marcel Grossmann Meeting, Berlin, 2006, pp. 2190- 2192.
- L.-X. Li and J. R. Gott, “A Self-Consistent Vacuum for Misner Space and the Chronology Protection Conjecture,” Physical Review Letters, Vol. 80, No. 2, 1998, pp. 2980-2983.
- M. S. Morris, K. S. Thorne and M. Yursever, “Wormholes, Time Machines and the Weak Energy Condition,” Physical Review Letters, Vol. 61, No. 13, 1988, pp. 1446- 1449.
- M. S. Morris and K. S. Thorne, “Wormholes in SpaceTime and their Use for Interstellar Travel: A Tool for Teaching General Relativity,” American Journal of Physics, Vol. 56, No. 5, 1988, pp. 395-412. doi:10.1119/1.15620
- R. A. Daly, S. G, Djorgowski, K. A. Freeman, M. P. Mory, C. P. O’Dea, P. Kharb and S. Baum, “Improved Constraints on the Acceleration History of the Universe and the Properties of Dark Energy,” The Astrophysical Journal, Vol. 677, No. 1, 2008, pp. 1-11;
- A. G. Riess, et al., “New Hubble Space Telescope Discoveries of Type Ia Supernovae at Z>=1: Narrowing Constraints on the Early Behavior of Dark Energy,” The Astrophysical Journal, Vol. 659, No. 1, 2007, pp. 98-121.
- A. Einstein and N. Rosen, “The Particle Problem in the General Theory of Relativity,” Physical Review, Vol. 48, No. 1, 1935, pp. 73-77. doi:10.1103/PhysRev.48.73
- P. F. González-Díaz, “Wormholes and Ringholes in a Dark Energy Universe,” Physical Review, Vol. D68, No. 8, 2003, pp. 084016-1-084016-11.
- S. Robles-Pérez, P. Martín-Moruno, A. Rozas-Fernández and P. F. González-Díaz, “A Dark Energy Multiverse,” Classical and Quantum Gravity, Vol. 24, No. 10, 2007, pp. F41-F45 doi:10.1088/0264-9381/24/10/F01
- L. Dyson, M. Kleban and L. Susskind, “Disturbing Implications of a Cosmological Constant,” Journal of High Energy Physics, Vol. 210, 2002, pp. 11-38.
- L. Dyson, M. Kleban and L. Susskind, “Cosmic Attack of the Boltzmann Brains,” New Scientist, Vol. 195, No. 2617, 2007, pp. 26-29.
- D. Overbye, “Big Brain Theory: Have Cosmologists Lost Theirs?” New York Times, 15 January 2008. http://www.nytimes.com/2008/01/15/science/15brain.htm
- M. Chown, “Into the Void,” New Scientist, Vol. 196, No. 2631, 2007, pp. 34-37. doi:10.1016/S0262-4079(07)62977-7
- J. A. Wheeler, “Bohr, Einstein and the Strange Lesson of the Quantum,” In: R. Q. Elvee, Ed., Harper and Row, New York, 1981.
- P. F. González-Díaz and C. L. Sigüenza, “Phantom Thermodynamics,” Nuclear Physics, Vol. B697, No. 1-2, 2004, pp. 363-386.

