Journal of Modern Physics
Vol.2 No.1(2011), Article ID:3765,4 pages DOI:10.4236/jmp.2011.21005
Quantum Physics Can Be Understood in Terms of Classical Thermodynamics
1-6-3, Mitsuya-kita, Yodogawa-ku, Osaka, Japan
E-mail: tom_miya@plala.or.jp
Received November 2, 2010; revised December 5, 2010; accepted December 9, 2010
Keywords: Boltzmann distribution, Maxwell’s Demon, Wagner equation, Nernst-Planck equation, additional thermodynamic law
ABSTRACT
Quantum physics can be understood in terms of classical thermodynamics, which is already considered to be a complete field. However, inconsistencies in classical thermodynamics have been discovered in the area of solid-oxide fuel cells (SOFCs). The use of samarium-doped ceria (SDC) electrolytes in SOFCs lowers the open-circuit voltage (OCV) below the Nernst voltage (Vth). The low OCV is calculated with Wagner’s equation, included in the Nernst-Planck equation, which is based on the first and second thermodynamic laws. Experimental and theoretical limitations of Wagner’s equation have been discovered. Considering the separation of the Boltzmann distribution and Maxwell’s Demon, only carrier species having sufficient energy to overcome the activation energy can contribute to current conduction, as determined by incorporating different constants in the definitions of the chemical and electrical potentials. This means that an additional thermodynamic law is needed. Furthermore, quantum physics can be explained by the additional thermodynamic law.
1. Introduction
Solid-oxide fuel cells (SOFCs) directly convert the chemical energy of fuel gases, such as hydrogen or methane, into electrical energy. In SOFCs, a solid-oxide film is used as the electrolyte. Oxygen ions serve as the main charge carriers in the electrolyte. In these cells, YSZ (yttria-stabilized zirconia) is typically used as the electrolyte material, at operating temperatures of 873- 1,273 K. Lower operating temperatures could extend the lifespan of the cells and enable the use of electrolyte materials with higher ionic conductivities, such as Sm-doped ceria electrolytes (SDC).
However, the open-current voltage (OCV) of an SDC cell is about 0.8 V, which is lower than the Nernst voltage (Vth = 1.15 V) at 1,073 K. This low OCV value is considered to be due to the low value of the ionic transference number (tion), as can be explained by inspection of Wagner’s equation [1]:
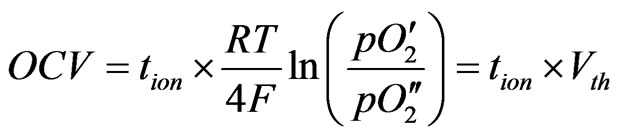 (1)
(1)
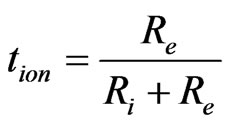 (2)
(2)
where R, T and F are the gas constant, the absolute temperature in Kelvin and the Faraday constant, respectively, 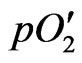 and
and 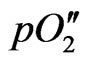 are the oxygen partial pressures at the cathode and anode, respectively, and Ri and Re are the ionic resistance and the electronic resistance of the electrolyte, respectively. In general, tion is not constant in the electrolyte. Therefore, Wagner’s equation is expressed as [2]:
are the oxygen partial pressures at the cathode and anode, respectively, and Ri and Re are the ionic resistance and the electronic resistance of the electrolyte, respectively. In general, tion is not constant in the electrolyte. Therefore, Wagner’s equation is expressed as [2]:
 (3)
(3)
In the application of Equation (3), the experimental verification of leakage currents is necessary [3-5]. Furthermore, a theoretical limitation of Equation (3) has been discovered [6]. The constant voltage loss without leakage currents observed in a mixed ionic-electronic conducting (MIEC) dense anode was already proposed by modifications of Wagner’s equation [7]. Wagner’s equation is included in the Nernst-Planck equation, which is based on the first and the second thermodynamic laws. This means that an additional thermodynamic law is needed. Furthermore, the relationship between quantum physics and thermodynamics is explained.
2. The Modification of Wagner’s Equation
The modifications of Wagner’s equation are explained by considering the separation of the Boltzmann distribution [7]. The Boltzmann distribution of oxygen ions is shown in Figure 1. Ions with an energy greater than the ionic activation energy become carriers that can escape from the electrolyte. Because the Boltzmann distribution cannot be separated using passive filters, a problem known as “Maxwell’s Demon,” the distribution in Figure 2 is forbidden.
The electrochemical potential should be identical be-
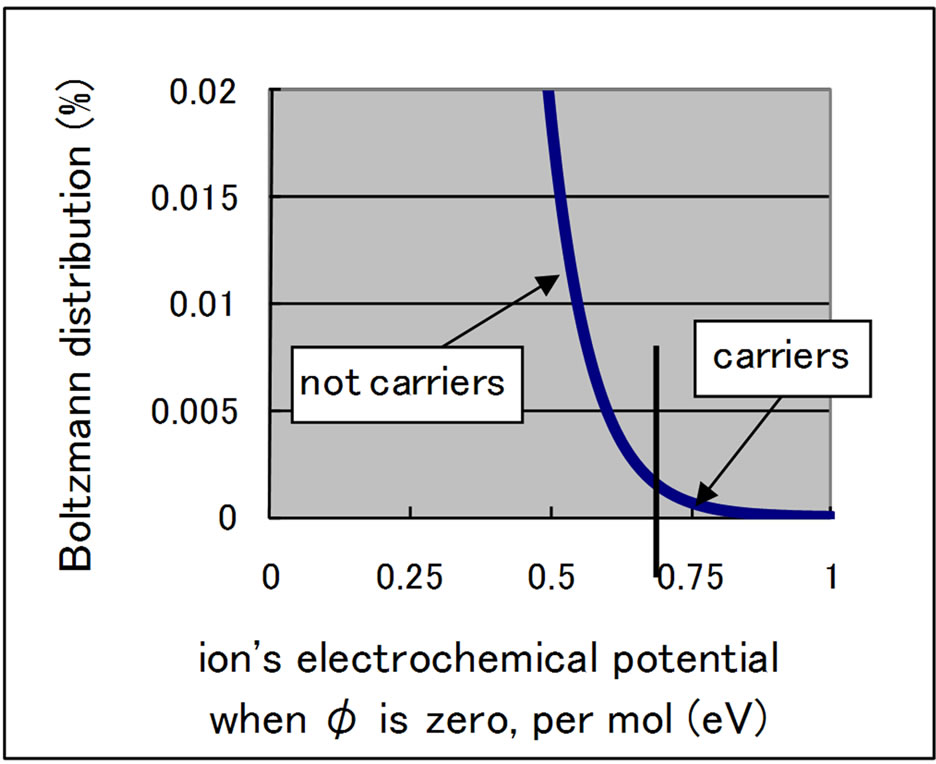
Figure 1. Boltzmann distribution of the electrochemical potential of ions.
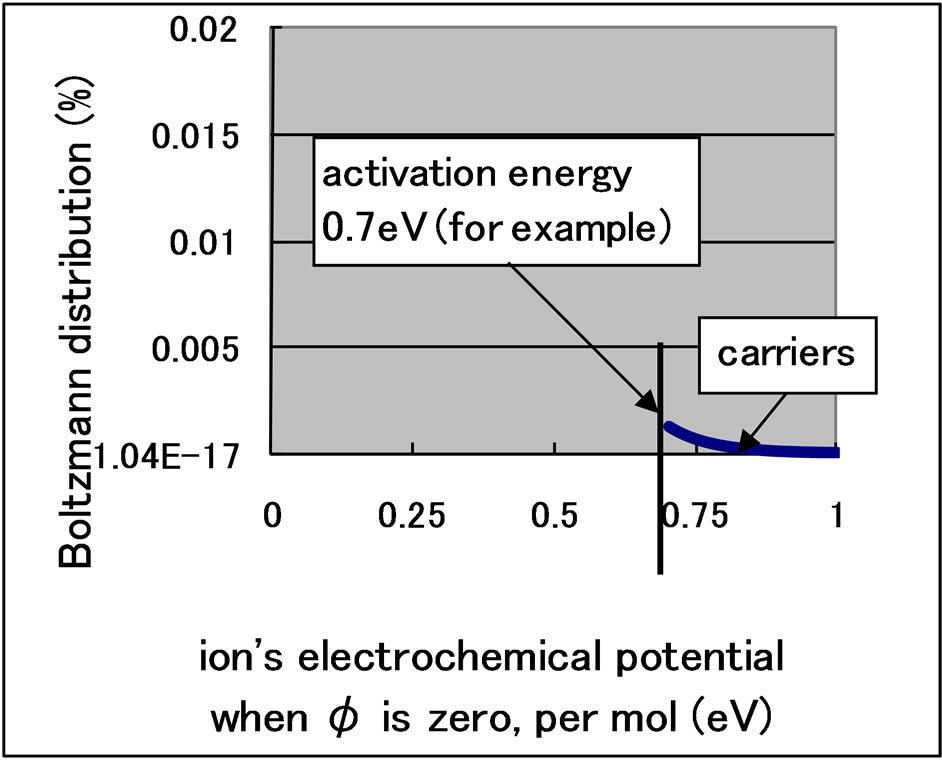
Figure 2. Incorrect distribution of hopping ions.
tween carriers and non-carriers.
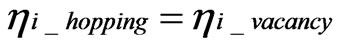 (4)
(4)
Here, ηi_hopping and ηi_vacancy are the electrochemical potentials of hopping ions and ions in vacancies, respectively. The correct distribution of hopping ions is shown in Figure 3. From the conventional theory:
 (5)
(5)
Here, N and Ea are Avogadro’s number and the activation energy of the oxygen ions, respectively. Equation 4 differs from Equation (5); thus, some transformations are required.
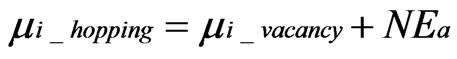 (6)
(6)
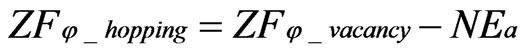 (7)
(7)
where μi_hopping, μi_vacancy, φ_hopping and φ_vacancy are the chemical potential of the hopping ions, that of the ions in vacancies, the electrical potential of hopping ions and the electrical potential of ions in vacancies, respectively. Equation (6) and Equation (7) are modifications of Wagner’s equation.
From Equation (7), for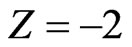 ,
,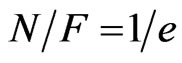 :
:
 (8)
(8)
In MIEC materials, φ_hopping is neutralized by free electrons and there is a voltage loss; therefore:
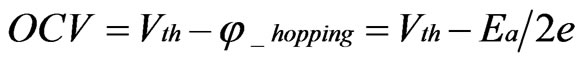 (9)
(9)
Equation (9) has previously been discovered empirically [8]. For example, using SDC electrolytes at 1,073 K, the Vth, Ea and OCV are 1.15 V, 0.7 eV and 0.80 V, respectively. Thus:
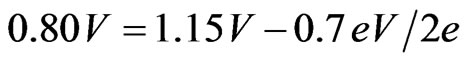 (10)
(10)
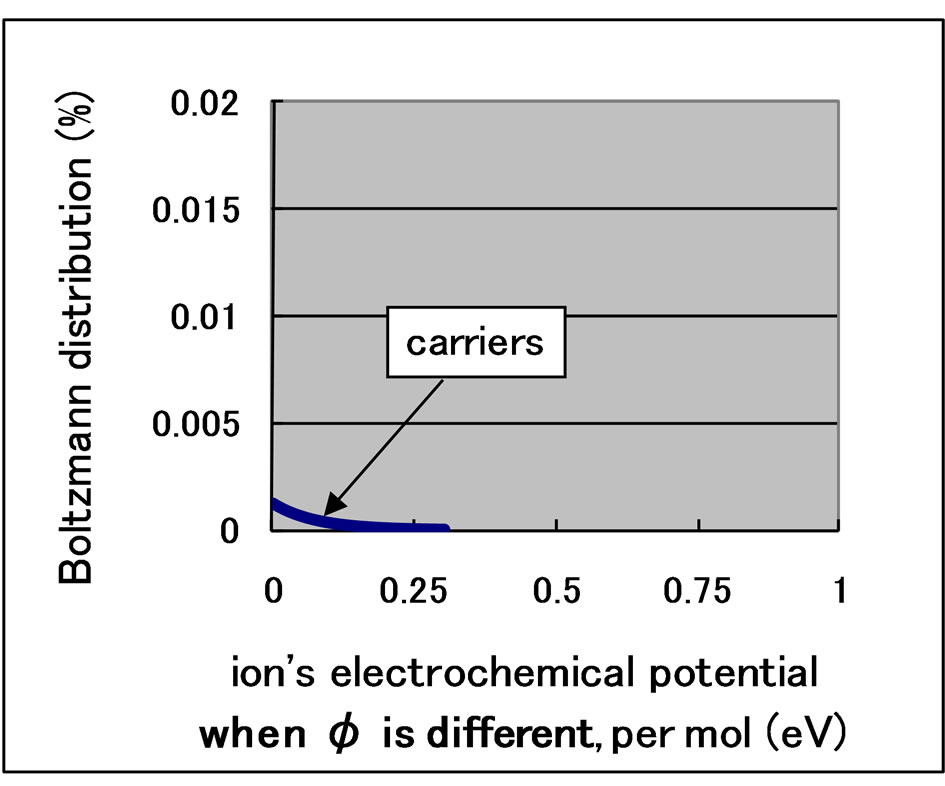
Figure 3. Correct distribution of hopping ions.
3. Relationship between the Additional Thermodynamic Law and Quantum Physics
The Nernst-Planck equation is:
 (11)
(11)
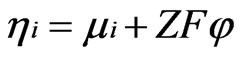 (12)
(12)
where Ji, si, mi and hi are the ionic current density, the ionic conductivity, the chemical potential of the ions and the electrochemical potential of the ions, respectively.
Using S (the action function), the Nernst-Planck equation can be written as:
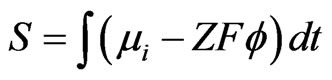 (13)
(13)
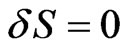 (14)
(14)
Considering the separation of the Boltzmann distribution and Maxwell’s Demon, the generalized expression from Equations (6) and Equation (7) is:
 (15)
(15)
Equation (15) holds for one hop but not zero, when Ea is not zero. Equation (15) is the generalized expression of the additional thermodynamic law. Instead of μi, ZFφ and 2 NEa, K.E. (kinetic energy), P.E. (potential energy) and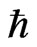 ω (where
ω (where  is the Planck constant and ω is the frequency) are used [9]:
is the Planck constant and ω is the frequency) are used [9]:
 (16)
(16)
Equation (16) is a characteristic expression in quantum physics. It means that hopping ions correspond to particles in the “R-process” described by Roger Penrose for the collapse of the wave function, and ions in the vacancies correspond to particles that are not measured. When the separation of the Boltzmann distribution by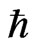 ω is needed in the R-process, Maxwell’s Demon should be considered. A different constant should then be incorporated in the definitions of K.E. and P.E.
ω is needed in the R-process, Maxwell’s Demon should be considered. A different constant should then be incorporated in the definitions of K.E. and P.E.
Here, 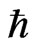 should be a boundary belonging to space and not to the particles. The situation is analogous to that in which Ea is a boundary for the lattice structure rather than for ions. When only hopping ions are considered to have a real existence, ions in vacancies should be described by the function of a complex number. Consequently, the additional thermodynamic law can be a generalization of quantum physics.
should be a boundary belonging to space and not to the particles. The situation is analogous to that in which Ea is a boundary for the lattice structure rather than for ions. When only hopping ions are considered to have a real existence, ions in vacancies should be described by the function of a complex number. Consequently, the additional thermodynamic law can be a generalization of quantum physics.
4. Verifying the Role of the Planck Constant
The value of Ea is different in the different lattices. If the value of 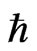 can change, its role can be verified. The possibility that
can change, its role can be verified. The possibility that 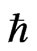 may not be a universal constant has been suggested, based on the fact that the Hubble constant has not been precisely determined. If the variation of
may not be a universal constant has been suggested, based on the fact that the Hubble constant has not been precisely determined. If the variation of  is confirmed,
is confirmed, 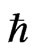 should belong to the spatial factor.
should belong to the spatial factor.
Furthermore, it is possible to verify the role of  theoretically. Einstein discovered four-dimensional spacetime, but many scientists have pointed out the fifth dimension in the space, which is an internal dimension and different from the other four dimensions. Thus,
theoretically. Einstein discovered four-dimensional spacetime, but many scientists have pointed out the fifth dimension in the space, which is an internal dimension and different from the other four dimensions. Thus, 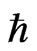 should be assigned to the fifth spatial dimension to separate observed particles from unobserved particles.
should be assigned to the fifth spatial dimension to separate observed particles from unobserved particles.
5. Summary
In the area of SOFCs, consideration of the separation of the Boltzmann distribution and Maxwell’s Demon requires the modification of Wagner’s equation (Equations 6 and 7). This means that an additional thermodynamic law (Equation 16) is required, which can be a generalization of quantum physics. Here, 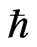 should be interpreted as a boundary in the spatial factor separating observed particles from unobserved particles. The situation is analogous to Ea forming a boundary in the lattice structure separating hopping ions from ions in vacancies. Furthermore, verifying the role of
should be interpreted as a boundary in the spatial factor separating observed particles from unobserved particles. The situation is analogous to Ea forming a boundary in the lattice structure separating hopping ions from ions in vacancies. Furthermore, verifying the role of 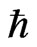 is discussed.
is discussed.
REFERENCES
- C. Wagner, “Beitrag zur Theorie des Anlaufvorgangs,” Zeitschrift für Physikalische Chemie, Vol. B41, 1933, p. 42.
- H. Rickert, “Electrochemistry of Solids—An Introduction”, Springer, Berlin, 1982.
- T. Miyashita, “Necessity of Verification of Leakage Currents Using Sm Doped Ceria Electrolytes in SOFCs,” Journal of Materials Science, Vol. 41, 2006, pp. 3183- 3184. doi:10.1007/s10853-006-6371-8
- W. Lai and S. M. Haile, “Electrochemical Impedance Spectroscopy of Mixed Conductors under a Chemical Potential Gradient: A Case Study of Pt|SDC|BSCF,” Physical Chemistry Chemical Physics, Vol. 10, 2008, pp. 865-883. doi:10.1039/b712473b
- W. Lai and S. M. Haile, “Impedance Spectroscopy as a Tool for Chemical and Electrochemical Analysis of Mixed Conductors: A Case Study of Ceria,” Journal of the American Ceramic Society, Vol. 88, No. 11, 2005, pp. 2979-2997. doi:10.1111/j.1551-2916.2005.00740.x
- T. Miyashita, “The Limitations of Wagner’s Equation in Solid-State Electrochemistry,” ECS Transactions, Vol. 33, 2010 (will be published).
- T. Miyashita, “Fundamental Thermodynamic modifications in Wagner’s Equation in Solid State Electrochemistry,” ECS Transactions, Vol. 28, 2010, pp. 39-49.
- doi:10.1149/1.3502443
- T. Miyashita, “Empirical Equation about Open Circuit Voltage in SOFC,” Journal of Materials Science, Vol. 40, 2005, p. 6027. doi:10.1007/s10853-005-4560-5
- G. Grossing, “Derivation of the Schroedinger Equation and the Klein-Gordon Equation from First Principles,” Foundations of Physics Letters, Vol. 17, 2004, pp. 343-362. arXiv:quant-ph/0205047v6

