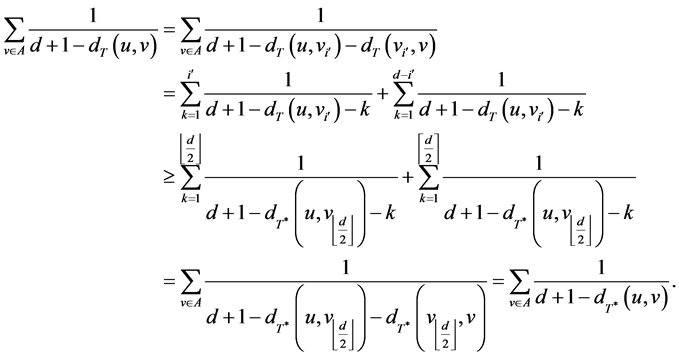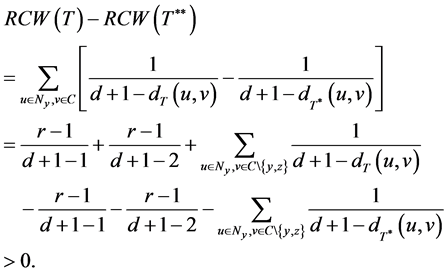Received 14 January 2016; accepted 23 February 2016; published 26 February 2016

ABSTRACT

The reciprocal complementary Wiener number of a connected graph G is defined as

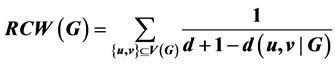
where 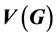is the vertex set. 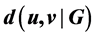is the distance between vertices u and v, and d is the diameter of G. A tree is known as a caterpillar if the removal of all pendant vertices makes it as a path. Otherwise, it is called a non-caterpillar. Among all n-vertex non-cater- pillars with given diameter d, we obtain the unique tree with minimum reciprocal complementary Wiener number, where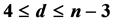. We also determine the n-vertex non-cat- erpillars with the smallest, the second smallest and the third smallest reciprocal complementary Wiener numbers.

Keywords:

Reciprocal Complementary Wiener Number, Wiener Number, Caterpillar

1. Introduction

The Wiener number was one of the oldest topological indices, which was introduced by Harry Wiener in 1947. About the recent reviews on matrices and topological indices related to Wiener number, refer to [1] - [4] . The RCW number is one of the hotest additions in the family of such descriptors. The notion of RCW number was first put forward by Ivanciuc and its applications were discussed in [5] - [8] .

Let G be a simple connected graph with vertex set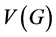. For two vertices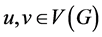, let 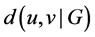denote the distance between u and v in G. Then, the RCW number of G is defined by

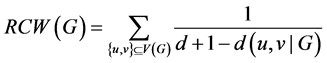
where d is the diameter and the summation goes over all unordered pairs of distinct vertices of G. Some properties of the RCW number have been obtained in [9] [10] .

A tree is called a caterpillar if the removal of all pendant vertices makes it as a path. Otherwise, it is called a non-caterpillar.

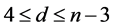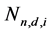For integers n and d satisfying, let be the tree obtained from the path 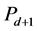labelled as

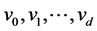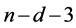by attaching the path and pendant vertices to vertex 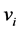for (see Figure 1). Let

In this paper, we show that among all n-vertex non-caterpillars with given diameter d, is the unique tree with minimum RCW number where. Furthermore, we determine the non-caterpillars with the smallest, the second smallest and the third smallest RCW numbers.

2. RCW Numbers of Non-Caterpillars

All n-vertex trees with diameter 2, 3, and are caterpillars. Let n and d be integers with and. Let be the class of non-caterpillars with n vertices and diameter d. Let be

the class of non-caterpillars obtained by attaching the stars at their centers and

pendant vertices to one center (fixed if it is bicentral) of the path, where, and for

(see Figure 2). Recall that Obviously, and

.

Let T be a tree. For and, let be the degree of u in T and be the

sum of all distances from u to the vertices in A, i.e.,. Here and in the following denotes the distance between vertices u and v in T.

Lemma 1 Let T be a tree with minimum RCW number in, where. Then,.

Proof. Suppose that Let be a diametral path of T. If d is odd,

we require that. Then at least one of has degree at least three. There are two cases.

Case 1. One of different from has degree at least three. Let be all the neighbors

outside except those of, where is a neighbor of. Let be the subtree of containing. be the tree formed from T by deleting edges and adding edges for

all. Obviously,. Let and. It is easily seen that

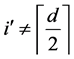
with equality if and only if. Since, for and with. We get

Then

with equality if and only if (which is only possible for odd number d). But, and thus if then. So for Thus

since for . It follows that. This is a contradiction.

Case 2. Any verter with and has degree two. Obviously,. Let be the (unique) path from x to in T such that. Since, we have. Let be the neighbors of y in T, where and.

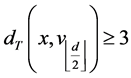
Let be the tree obtained from T by deleting edges and adding edges for all. Then. Let, Since for , we get

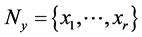
This is a contradiction.

By combining Cases 1 and 2, we find that is impossible. The result follows.

Lemma 2 Let with. Then

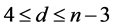
with equality if and only if.

Proof. Let T be a tree with the minimum RCW number in. Let be a diametral path of T.

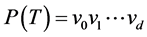
Suppose that there is a vertex with Let be the neighbors of u different from in T, where. Clearly, are pendant vertices for. Let be the tree

obtained from T by deleting edges and adding edges for. Obviously, Let, and Since for

, we get

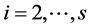
and then, this is a contradiction. Thus any vertex of T outside has degree at most two.

Suppose that there are at least two vertices of T outside with degree two. Let

with and let x be the neighbor of y which is different from in T. Let be the tree formed from T by deleting edge yx and adding edge. Obviously, Let Since and for, we get

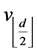
This is a contradiction. Thus there is exactly one vertex outside with degree two and all other vertices of T outside are pendant vertices. Then,.

By a direct calculation, we get

Combining Lemmas 1 and 2, we get

Theorem 1 Let, and Then

with equality if and only if.

Lemma 3 For, there is.

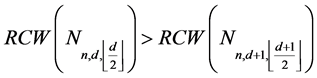
Proof. If d is even, then

If d is odd, then

The result follows.

Theorem 2 For, there is

And for any n-vertex non-caterpillar T different from ,

Proof. Let, where. If, then T is a non-caterpillar where

It follows that

and hence is monotonically decreasing for This implies

Now suppose that. By Theorem 1 and Lemma 3, there is

where equality holds if and only if We need only to show

Case 1. n is odd. Let and. Then there is

Case 2. n is even. Let Then there is

Thus, the proof is finished.

Cite this paper

YanliZhu,FuyiWei,FengLi, (2016) Reciprocal Complementary Wiener Numbers of Non-Caterpillars. Applied Mathematics,07,219-226. doi: 10.4236/am.2016.73020

References