Applied Mathematics
Vol.07 No.02(2016), Article ID:63514,11 pages
10.4236/am.2016.72015
An Evolutionary Approach for Personalized Therapy in Multiple Myeloma
Ariosto S. Silva1, Ashley Durand2, Maria C. Ribeiro1, Melissa Alsina3, Kenneth Shain3, Rachid Baz3
1Department of Cancer Imaging and Metabolism, H. Lee Moffitt Cancer Center and Research Institute, Tampa, FL, USA
2Department of Total Cancer Care, H. Lee Moffitt Cancer Center and Research Institute, Tampa, FL, USA
3Department of Malignant Hematology, H. Lee Moffitt Cancer Center and Research Institute, Tampa, FL, USA
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 December 2015; accepted 14 February 2016; published 17 February 2016
ABSTRACT
Most patients with multiple myeloma (MM) respond well to initial therapy, but invariably relapse due to evolution of resistant phenotypes. Here we examine the evolutionary dynamics of proliferation of resistant MM phenotypes during therapy. By applying computational models to data from three clinical trials for newly diagnosed MM patients, we have quantified the size and level of chemoresistance of subpopulations within the tumor burden in 124 patients, prior to and during therapy. Subsequently, we used the computational models to explore an alternative strategy of “adaptive therapy” (AT), which includes defined treatment holidays, to improve the duration of “controlled disease” (CD). Simulations showed that AT could prolong CD in all three trials: 50.0% vs. 11.1% 50-month CD for a single agent approach in older adults (P = 0.0123), 80.4% vs. 58.8% 60-month CD for a multi-agent bortezomib based therapy (P = 0.0082), and 54.0% vs. 24.0% 60-month CD for a multi-agent lenalidomide based therapy (P < 0.0001). Increases in duration of CD resulted from the stabilization of tumor burden, which in turn would delay the growth of chemoresistant sub-populations in patients with partial (PR), or very good partial response (VGPR). These computational algorithms suggest that AT may provide an alternative and feasible therapeutic management strategy in MM.
Keywords:
Multiple Myeloma, Adaptive Therapy, Evolutionary Dynamics, Competitive Release

1. Introduction
Multiple myeloma (MM) is a treatable but not curable disease of malignant plasma cells. Although many effective agents are currently available, resistance ultimately emerges, leading to uncontrollable tumor growth and patient death. Although some patients achieve complete responses, with undetectable tumor burden after therapy, between 50% and 75% reach a plateau of refractory disease [1] [2] , which is followed by tumor re-growth.
Here we examine the evolutionary dynamics that lead to proliferation of resistant phenotypes in MM. Our goal is to generate predictive models that anticipate adaptive strategies from tumors in individual patients, and use evolutionary principles to optimize therapy by delaying proliferation of resistant phenotypes. In general, we propose that every MM patient harbors pre-existing cancer cells that evade therapy through a combination of intrinsic and environment-mediated mechanisms [3] . By successively treating the patient with different therapeutic agents, eventually one or more subpopulations of multi-drug resistant cells are selected, and no other therapeutic alternatives are left. This is true even for patients with a complete response, for which no detectable minimum residual disease exists after initial therapy [4] .
These evolutionary dynamics are, in fact, well known. After Willem de Vlamingh discovered black swans in West Australia in 1697, the term was used to denote occurrences originally believed to be impossible, but ultimately found to be true. The “Black Swan Theory” proposes that low probability events, also called outliers, can have major impact in complex systems such as economy and ecology [5] . Similarly, it seems that in MM patients treated with high doses of several drugs that kill large numbers of cancer cells, there are “black swans” capable of withstanding highly effective combination therapies.
The therapeutic approach described here is based on the assumption of the pre-existence of therapy-resistant cells, and seeks to prevent the emergent growth of this refractory population for as long as possible. To be successful in a wide range of patients, this approach must also account for inter-patient heterogeneity, as the number and degree of resistance of these refractory cells appear to greatly vary from one patient to the other. Furthermore, our investigation cannot simply be confined to the MM cells, since much of the de novo resistance in MM patients is environmentally mediated, and thus determined by interactions between MM and the bone marrow microenvironment. Finally, we must consider that cancer cells not only interact with the host but also compete among themselves for resources. The need for angiogenesis for tumor growth, and the common necrotic, hypoxic and acidic niches in tumors are evidence that such competition exists [6] .
In previous works, our group and others have proposed that intra-tumoral evolutionary dynamics, including competition among tumor subpopulations, could be exploited to improve the duration of response. By using the chemosensitive population as an obstacle to maintain the chemoresistant minority quiescent [4] [7] -[10] , this approach, termed adaptive therapy (AT), aims for stabilization of the tumor burden with minimum use of chemotherapeutic agents. There are, however, two theoretical conditions for AT to be successful: 1) the size of the chemoresistant population must be small compared to the size of the chemosensitive population, and 2) the chemoresistant population must be equally or less fit than the chemosensitive population in absence of therapy. This second requirement is a natural consequence of the “cost of resistance”, such as energetic waste of basal efflux pump activity [10] or longer cell cycle due to over-active DNA repair activity [11] . Combining these two conditions ensures that the chemosensitive cells constrain the growth of the chemoresistant ones, and overgrow them during therapy “holidays”.
We examined the evolutionary dynamics of resistance in 124 MM patients from three clinical trials. We have developed a patient-specific computational model to determine the ratio of the chemosensitive and chemoresistant tumor burden, as well as the level of sensitivity of each sub-population to the therapeutic regimens. With this information, the model simulated the expected response of the same patient to an alternative AT regimen, by introducing “therapy holidays” (weeks without treatment) whenever the tumor burden decreased or remained stable.
Due to the nature of the AT regimen, which leads to controlled oscillations of the tumor burden, the term progression-free survival (PFS) may not be used. Throughout this manuscript, the term duration of controlled disease (CD) is used instead, to refer to the interval of time prior to tumor growth under AT during maximum frequency (no “holidays”). Under standard regimen, CD and PFS are synonyms.
The simulations projected a significant increase in the duration of controlled disease (CD), mainly in the patients that would have had a PR or VGPR under standard therapy, indicating that these patients would benefit from characterization of clonal variation in drug sensitivity prior to initiation of treatment.
The models were also used to address two important questions for an eventual clinical trial evaluating AT in MM: the first would be at what level the tumor burden should be stabilized. Since the tumor burden inversely correlates with patient health, there is a need to keep this burden at a minimum level, but not so low that it would allow unrestrained proliferation of resistant cells.
The second question would be whether fewer or more agents should be combined at once. While some authors propose that combinations of multiple agents could increase chances of complete response [12] , others have indicated that additional agents increase duration of PFS, but have no effect in overall survival [13] . We have also noted in a retrospective study that high-risk patients may actually have a worse survival when treated with combinations of 3 or more agents as compared to treatment with sequential therapy using two agents [14] .
These conflicting observations only reinforce the importance of using formal frameworks, such as evolutionary computational models, for elaborating and testing hypothesis comparing the outcomes of clinical trials in multiple myeloma.
2. Methods
2.1. Ethics Statement
This study retrospectively analyzes clinical data (therapy response) collected from three clinical trials at the H. Lee Moffitt Cancer Center, properly approved by the Institutional Review Board (MCC# 16018, MCC# 15399, and MCC# 14986), and published in ClinicalTrials.gov website (NCT00750815, NCT00617591, and NCT 01054144). The medical records were de-identified and only the following clinical-relevant information was reviewed: treatment administered, cytogenetics, and assessment of tumor burden using serum and urine electrophoresis results and serum free light chain testing.
2.2. Clinical Trials
Only patients with three or more paraprotein measurements were included in the simulations, this excluded 11 patients. The first trial (Rev) included 18 newly diagnosed older adults who received single agent lenalidomide with the addition of dexamethasone or prednisone in case the patient’s disease progressed or was deemed stable after 2 cycles, respectively [15] . The second trial (CVDD) enrolled 56 newly diagnosed patients who were treated with a cyclophosphamide, bortezomib, liposomal doxorubicin, and dexamethasone regimen [16] . The third trial (Dd-R) enrolled 50 newly diagnosed patients who received liposomal doxorubicin, low frequency dexamethasone, and lenalidomide [17] .
For the Rev trial, the second agent was only introduced between 3 and 21 cycles after the first, and only in seven patients, thus we were able to estimate the level of resistance of the first and the second drug individually. For the two other trials, all agents were administered within a cycle, and the tumor burden was measured at the end of each cycle. Thus, it was impossible to determine the effect of each chemotherapeutic agent individually. For these two trials, the sensitivity was quantified for the combination of agents.
2.3. Mathematical Model of MM Therapy
The model used to simulate the growth of cancer sub-populations in each patient, and their chemosensitivity to therapy, was previously described in Silva et al. [10] . Briefly, two sub-populations were modeled, each with a size, a doubling time, and a level of sensitivity to each of the chemotherapeutic agents or combinations used in the trial. The maximum theoretical growth rate of the entire tumor burden was estimated from the labeling index commonly observed in MM patients (~1% - 3%). Intra-tumoral competition was modeled by Equation (1), which determines that bigger populations have higher chance of maintaining, or increasing their share in the total population, than smaller ones.
 (1)
(1)
Ni(t) is the size of the sub-population “i” at time “t”, while Ni(0) is initially unknown, the sum of all Ni(0) equals to the total tumor burden, measurable by paraprotein levels, at the beginning of treatment. L.I. is the labeling index (here assumed as 1%), dt is the interval used in the numerical calculations of the simulation, which for this manuscript was used as one day. Rx is the average drug concentration to which the patient was exposed during the interval dt. IC50i is the drug concentration that would induce a 50% decrease in the viability of the
sub-population “i” in the interval 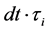 represents the doubling time of each sub-population.
represents the doubling time of each sub-population.
In the AT regimen herein proposed, patients start on a regimen of one week on therapy and three weeks off. Two thresholds were arbitrarily defined: the tumor level after one cycle of therapy was defined as the upper threshold, while the tumor level after the second cycle as the lower threshold. The frequency increases (for instance two weeks on, two weeks off, then three weeks on and one week off) in case the tumor burden increases beyond the upper threshold. Conversely, if the tumor burden decreased or stabilized below the lower threshold, the algorithm reduced the frequency of therapy by adding “holidays”. The regimen was adjusted every month, depending on the results of the tumor burden assessment, as estimated by the myeloma paraprotein concentration. This hypothetical regimen was herein proposed due to its use of standard doses, which increases the possibility of rapid clinical implementation.
In trials where agents are administered only once during a cycle, it is possible to implement the holidays at a cycle level, for instance three cycles on, one cycle off. Notably, other, more sophisticated algorithms, including dose adjustment, are also possible.
The model was simulated by numerically solving a system of N difference equations (Equation (1)), where N is the number of sub-populations in the tumor burden, with time steps of 1 day. We implemented a Genetic Algorithm (GA) using the library JGAP (http://jgap.sourceforge.net/) to fit the model parameters to the clinical measurements of tumor burden during treatment. The model parameters fit by the GA were: the size of each sub-population (Ni(t)), the doubling time of cells in each sub-population (τi), and the chemosensitivity of each sub-population to chemotherapy (IC50i). Briefly, this algorithm creates a random group of possible solutions (2000), and iteratively evaluates the goodness of fit of the different solutions, attributing the highest scores to those with the best fit (shortest distance between the simulated curves and observed tumor burden). The best solutions increase their frequency in the pool of possible solutions, while the lowest scores are removed. Spontaneous “mutations” of these parameter values add diversity to the population. The final product of this genetic algorithm is the set of sub-population sizes and chemosensitivity parameters which, when incorporated into the mathematical model, generate “spaghetti models” of patient response to actual or hypothetical therapeutic regimens (Figure 1).
2.4. Statistical Analysis
For each patient, 20 simulations were calculated (10 for standard and 10 for AT regimen), and the mean and SEM were graphed in the “spaghetti models”. To compare the standard and the personalized regimen with holidays, we used duration of controlled disease (CD) as metric: the patient was considered to have progressive disease when the mean of the total tumor burden increased monotonically for two consecutive months during maximum tolerated therapy. For the standard regimen, CD and PFS are synonyms. For AT, progression occurs when the tumor grows under the maximum frequency of AT (no holidays).
The 60-month percentage of controlled disease of the patients from the three trials (Rev, Dd-R, and CVDD), as well as the statistical difference between the two regimens, were calculated using the software Prism 5 (Graph Pad) and the Log-rank (Mantel-Cox) test.
3. Results
Figure 1 shows three examples of patient tumor response to therapy: the first example shows a patient with undetectable minimal residual disease after therapy. The second example shows a partial response to therapy. In the last example, a patient has an initial very good response, but eventually reaches a plateau and relapses.
In each example of Figure 1, three curves are shown: the solid dark gray disks represent the actual data points of paraprotein levels from monthly blood or urine exams. The dark curve (MTD) represents the computational model fit for tumor progression during standard therapy. As the simulation moves further from the last actual data point, the prediction curve fans out, thus the increase in the error bars. The light gray curve (AT) represents the simulation of the same patient if he or she had been treated with the Adaptive Therapy (AT) approach proposed in this work, with “therapy holidays”. The error bars observed in this curve are due to the multiple possible explanations (size and level of resistance of different sub-populations) found by the genetic algorithm to ex-
Figure 1. Simulations of adaptive therapy compared to MTD and actual patient response. Three different patterns were observed in the patients in this study. The first (top left) consisted of patients who had a complete response to treatment and showed no signs of residual burden according to para-protein levels. The second group (top right) consisted of patients who had a less than partial response, or were de novo refractory to therapy. The third group (bottom left) consisted of patients with a very good or partial response to therapy followed by relapse. Theoretically only the third group would benefit from AT, since this regimen would maintain the chemoresistant sub-population quiescent and prolong the period of response to therapy, and consequently overall survival. The overall survival of the first group could not be estimated by the mathematical model, due to the undetectable minimum residual disease. For patients in the second group, AT eventually escalates to MTD as the chemoresistant tumor burden is too big to be contained by the chemosensitive sub-population. An example of the intratumoral competition enticed by AT is shown on bottom right, where MTD eradicates the therapy-sensitive cells (MTD(S)) but sets free the refractory tumor (MTD(R)) resulting in tumor regrowth. AT maintains the sensitive tumor burden (AT(S)) below a certain level, what maintains the resistant portion of the tumor quiescent (AT(R)).
plain the patient tumor burden.
The lower-right panel in Figure 1 dissects the example of the patient #26 in the trial Dd-R. The figure shows the actual m-protein measurements (ACTUAL), as well two sub-populations, one chemoresistant (R), and one chemosensitive (S) progressing under standard regimen (MTD) or Adaptive Therapy (AT). Under standard regimen the chemosensitive sub-population is depleted around 6 months after initiation of therapy, which reduces intra-tumoral competition and allows the chemoresistant clone to regrow (black solid line). Alternatively, the use of “therapy holidays” maintains the chemosensitive cells oscillating at manageable levels, which in turn maintains the chemoresistant cells quiescent throughout the entire course of the simulation (60 months).
Figure 2 depicts the CD curves generated by the computational models for the three trials, under either standard (MTD) or AT regimens. The single-agent trial (Rev) had a 50-month CD of 11.1% for MTD, and 50% for AT. The three-agent trial (Dd-R) had a 60-month CD of 24% for MTD and 54% for AT, while the four-agent trial (CVDD) had 60-month CD of 58.8% and 80.4% for MTD and AT, respectively. These simulations suggest that AT in these three clinical trials may provide superior outcome to the preferred standard of care regimen, which is induction, followed by high-dose melphalan and bone marrow transplantation in eligible patients. Namely, in prior studies, the 3-year post transplant PFS for VTD (bortezomib, thalidomide, dexamethasone) induction was 68%, TD (56%), PAD (bortezomib, adriamycin, dexamethasone, 48%), and TAD (42%) [18] .
These results indicate that, while the addition of new agents to MM treatment indeed prolongs CD, adjusting the frequency of administration of these agents in order to stabilize tumor burden, rather than continuous administration, may increase CD and ultimately overall survival significantly further.
The rationale behind the combination of multiple agents under AT is described in the Figure 3: the phenol-
Figure 2. Computational simulations of duration of controlled disease (CD) in patients treated with standard (MTD) and adaptive therapy (AT) regimens. A computational model was used to extrapolate the response of MM patients for the trials under single agent lenalidomide (Rev), pegylated liposomal doxorubicin, low frequency dexamethasone & lenalidome (Dd-R), and cyclophosphamide, bortezomib, pegylated doxorubicin, and dexamethasone (CVDD), under standard (MTD), and an adaptive therapy regimen that included “holidays” when the patient burden declined below a pre-determined threshold (AT). The simulations show a statistically significant difference in duration of CD (P = 0.0123) according to Log-rank (Mantel-Cox) Test, with a 50-month CD rate of 50% for adaptive, versus 11.1% for standard regimen, for single agent lenalidomide (Rev). Similarly, the simulations over a 60-month period showed a statistically significant difference in 60-month CD (P < 0.0001) according to Log-rank (Mantel-Cox) Test for Dd-R (54% vs. 24%). For CVDD, P = 0.0082, and 60-month CD was 80.4% vs. 58.8%.
Figure 3. The combination of multiple agents reduces the size of the resistant subpopulation and prolongs controlled disease (CD) under adaptive therapy, but not necessarily in standard regimen (MTD). (Top left) The use of a single agent kills most of the cancer cells, but leaves behind a significant number (black and white diagonal disk), which will be responsible for relapse. (Top middle, and right) By combining multiple agents, the number of cells capable of resisting all agents is significantly smaller, however, relapse still occurs (bottom left). While the rate of complete response is higher in triplets and quadruplets, no assumptions can be made on overall survival. Under AT, the duration of controlled disease is inversely related to the size of the resistant sub-population, thus the more agents added, while adjusting dosing or frequency of administration, the longer would be CD (bottom right).
typic space of the tumor burden of a hypothetical patient is represented as the larger gray disk. The smaller disk, with black and white diagonals, in the first example, represents the cells that are resistant to the single agent regimen. As more agents are added to the regimen, this multi-drug resistant area becomes smaller. In the example of this figure, the hypothetical patient would have a “partial response” with one agent, a “very good partial” response with three agents, and a “complete response” with four. In all three cases, however, there would be a residual of resistant cells and hence relapse. Depending on the rate of regrowth of the resistant burden, even a “complete response” may not lead to actual difference in overall survival, or paradoxically may actually lead to a reduced overall survival, as the emergent cells are pan-resistant. As previously mentioned, however, the AT regimen is more effective when the resistant sub-population is smaller, and thus the combination of multiple agents, but at doses and frequencies that would prevent tumor growth, rather than eradicating it, would be a potential strategy to initiate trials with the smallest possible fraction of resistant cells.
We next tested if the herein-described computational model could be used to estimate the resistant subpopulation at earliest stages of treatment. For this purpose, we used the same data set for a given patient for multiple simulations, but in each simulation a smaller number of data points were provided, to emulate how well the computational model would predict time to progression after three months of therapy, compared to 9 months, for instance. Figure 4 illustrates this approach for the patients 13, 19, 31, and 59 of the trial Dd-R: gray disks represent the actual data points (ACTUAL), gray and black solid lines represent the curves modeled from 3 and all data points, respectively.
These results indicate that, while such models can be used to study the optimization of therapeutic regimens using retrospective data, the exact quantification of the resistant sub-population is only possible when therapy has significantly reduced the tumor burden to a point where the resistant sub-population fraction has become large enough to affect the total tumor response. At this point, however, AT becomes less efficient. However, once models have been created for a cohort of patients under a specific regimen and agent combination, it is
Figure 4. Model predictions can be improved with more data points or with a training set. A key question to be addressed by a clinician in an AT trial would be: “how low should the tumor burden be maintained?” To address this question, simulations for four patients of the CVDD trial were performed with different numbers of data points provided to the model, in order to determine how early a clinician would be capable of detecting patient relapse. The results show that simulations converge to the actual amount of minimum residual disease (actual data points shown as gray disks) as more data points are obtained (solid black line). However, by training the genetic algorithm with the maximum and minimum range of the parameters of Equation (1), from all patients in a particular trial, it is possible to narrow down the predictions, and make an “educated guess” as early as at the third data point (solid gray line).
possible to “train” the GA to work within a narrower range of parameters, which significantly improves the estimations of minimum residual disease as early as three months within treatment.
4. Discussion
While patients with MM usually respond well to initial therapy, evolution of resistance in the MM populations is virtually inevitable, leading to tumor progression and death. Here we examine the evolutionary dynamics of drug sensitivity and resistance in a cohort of 124 patients. Our computational models have indicated that an alternative, evolutionarily based regimen, would have increased duration of controlled disease (CD) in all three trials, and the patients most benefited would be the ones with a small, but detectable therapy refractory sub-population.
According to IMWG classification [19] this subgroup of patients would be categorized as VGPR (Very Good Partial Response, ≥90% reduction of tumor burden) or PR (Partial Response, ≥50% reduction of tumor burden). These patients are believed to have a worse prognosis than patients with Complete Response (CR), although some controversy still exists on the value of CR in overall survival [1] . The results from these simulations, however, show that patients who had a VGPR or PR under a standard regimen, could have had a longer progression-free survival if they had undergone a less intense regimen, which included “therapy holidays” whenever the tumor burden stabilized or decreased.
The rationale behind this conclusion is that these patients harbor a minimum residual disease, which is refractory to the agent combination administered. By using a less aggressive therapeutic regimen, the selection for these refractory cells will take longer.
Another question addressed by the models was the effect of the combination of multiple agents in the increase of CD. The computational simulations suggest that, while the inclusion of more agents would increase CD under a standard regimen, the longest CD are observed when these agents are used under an AT regimen, theoretically reaching CD levels superior to induction followed by bone marrow transplantation. The explanation of the synergy between AT and multiple-agent combination is as follows: the smaller the size of the resistant subpopulation, the stronger will be the growth-suppression effect of the chemosensitive clone. The more agents are present in the regimen, the smaller will be the sub-set of de novo resistant cells (Figure 3).
Thus, the ideal theoretical regimen, the one with longest duration of controlled disease, would be one that included more agents, but administered them at a dose/frequency that maintained the disease stable, instead of seeking CR. While this conclusion might me counterintuitive, it is possibly the reason behind the controversial results between trials that favor therapeutic rationing (save drugs for later) and those who propose the use of as many agents as possible [12] .
We have addressed whether these computational models could be used during the first cycles of therapy, to estimate the size of the chemoresistant burden. The goal would be for the model to instruct the clinician on the minimum stable tumor burden that would still delay relapse. We have shown that, by restricting the model parameters by using the maximum and minimum ranges observed in a cohort of patients treated under the same regimen, it was possible to significantly reduce the time required to estimate minimum residual disease, to as little as three months (Figure 4, solid gray line). Consequently, in a clinical trial, the data from early-accrued patients could be used to train the models, and more accurately predict the therapy response of newly accrued patients. In standard of care patients, historical data from patients previously treated with the same regimen could also be used to enrich these models and make them more predictive.
Another approach to use such computational models as predictive tools for personalized treatment in multiple myeloma would be to develop experimental platforms, to estimate the size and level of resistance of sub- populations within the tumor burden, prior to actual therapy. We have recently proposed a proof-of-principle that would integrate ex vivo chemotherapy response of myeloma cells from MM patients, into personalized models of therapy response [20] . While such an approach is limited to agents with ex vivo activity, it overcomes many of the early ex vivo drug screening colony formation assays [21] , such as required number of cells and the time required for colony formation [22] , and thus could be used as a predictive biomarker for an AT prospective clinical trial.
The diversity of patterns of therapy response on the patients here studied, suggest a hypothesis for the commonly observed difference in relapse rate between standard (SR) and high-risk (HR) MM patients. We hypothesize that MM cells in HR patients suffer from inherently higher genetic instability, which is evidenced by the cytogenetic abnormalities that are the hallmark for these patients. Such genetic instability would thus induce an increased mutation rate, and consequently, a more phenotypically heterogeneous population (Figure 5). While most random mutations are deleterious and confer loss of function, an increased mutation rate also generates rare mutants that are fitter than the parental cells [23] . This concept was recently been independently proposed by Keats et al. [24] , although at a genetic level, where tumor samples from HRMM patients have shown a larger number of copy number variations when compared to SRMM patients, resulting in different sub-populations with diverse levels of chemosensitivity and mutually competing for dominance of the tumor burden. Upon therapy, the response of SR patients should be similar to the one depicted in Figure 5 (bottom, left): homogeneous with a constant relative decrease of tumor burden. The response from a HR patient, on the other hand, would be a pattern of quick response, as the clones with deleterious mutations are promptly killed by therapy, followed by relapse, as the chemoresistant clones re-grow the original tumor (Figure 5, bottom, middle).
According to this hypothesis, HR patients, who have higher risk of early relapse, would be the best candidates for AT, since their chances of achieving CR are lower than in SR patients, but their refractory tumor burden may be small enough to be maintained quasi-quiescent by AT.
While the genetic and molecular mechanisms behind progression and evolution of chemoresistance in MM are complex, we propose a simple framework for classifying MM patients according to their clinical response,
Figure 5. A hypothesis for different response patterns between standard and high-risk MM patients. (Top) Cancer cells in standard risk (SR) MM patients are more genetically stable, with a chemosensitivity distribution tight around the mean. Cancer cells from high-risk MM patients (HR) have higher genetic instability, as evidenced by cytogenetic abnormalities, and thus have a wider phenotypic chemoresistance distribution. As most random mutations are deleterious, most of the MM cells in HR patients are less fit than their parental cells, shifting the chemosensitivity distribution to the left. Upon treatment initiation, and during the first cycles of therapy, all cells in the dashed box “A” are killed. As treatment continues, all cells in the “B” range of chemosensitivity die. Cells in “C” are refractory to therapy, and are responsible for relapse. (Bottom) According to this simple model, the slow, but steady initial response of SR patients are due to a more homogeneous tumor population, while the fast initial response, followed by quick relapse in HR patients is caused by the inherent genetic, and phenotypic heterogeneity of its tumor population. The three parameters that rule the therapy response of a MM patient are thus: δ (the rate of decrease of the sensitive population), μ (the minimum residual disease), and ρ (the rate of re-growth of the resistant sub-population). The evolutionary therapeutic regimens here proposed seek to delay relapse by extending δ as much as possible, and ensuring that the refractory burden μ grows at the slowest possible rate, orders of magnitude lower than ρ.
and suggest an algorithm for adjusting therapeutic regimens to specific properties of the tumor burden, namely the chemosensitivity of the chemosensitive sub-population, the size, and the re-growth rate of the chemoresistant population (Figure 5, bottom, right).
It is important to note that the values of tumor burden used for these simulations were based on measurements of blood or urine para-protein, which is the current standard of care. While in most patients there is a direct correlation between number of myeloma cells and amount of secreted para-protein, in some patients this is not the case. For instance, the phenomenon of light chain escape occurs when, during the treatment, the secretion of intact immunoglobulin shifts to free-light chains only, and is estimated to occur in approximately 3% of MM patients [25] . Such cases can still be modeled, but it is necessary to normalize the measurements in different units prior and post the shift.
5. Conclusion
The work here presented is still preliminary, but it describes a framework for personalization and optimization of chemotherapeutic regimens, based on computational models, and clinical response of MM patients. The improvements in the duration of controlled disease here described, although still theoretical, support the idea that optimization of therapy regimens, tailored to the needs and characteristics of each patient, may lead to meaningful progresses in myeloma therapy.
Acknowledgements
First and foremost we would like to thank the patients at H. Lee Moffitt Cancer Center who consented to provide clinical data and samples to the Total Cancer Care database, which was used in this study. This research was funded by the H. Lee Moffitt Cancer Center Physical Sciences in Oncology (PSOC) Grant (1U54CA 193489-01A1) and by H. Lee Moffitt Cancer Center’s Team Science Grant. This work has been supported in part by the Translational Research Core Facility at the H. Lee Moffitt Cancer Center & Research Institute, a NCI designated Comprehensive Cancer Center (P30-CA076292). Access to primary cells was made possible through the Total Cancer Care Protocol at the Moffitt Cancer Center.
Cite this paper
Ariosto S.Silva,AshleyDurand,Maria C.Ribeiro,MelissaAlsina,KennethShain,RachidBaz, (2016) An Evolutionary Approach for Personalized Therapy in Multiple Myeloma. Applied Mathematics,07,159-169. doi: 10.4236/am.2016.72015
References
- 1. Harousseau, J.L., Attal, M. and Avet-Loiseau, H. (2009) The Role of Complete Response in Multiple Myeloma. Blood, 114, 3139-3146.
http://dx.doi.org/10.1182/blood-2009-03-201053 - 2. Barlogie, B., Shaughnessy, J., Tricot, G., Jacobson, J., Zangari, M., et al. (2004) Treatment of Multiple Myeloma. Blood, 103, 20-32.
http://dx.doi.org/10.1182/blood-2003-04-1045 - 3. Meads, M.B., Gatenby, R.A. and Dalton, W.S. (2009) Environment-Mediated Drug Resistance: A Major Contributor to Minimal Residual Disease. Nature Reviews Cancer, 9, 665-674.
http://dx.doi.org/10.1038/nrc2714 - 4. Gatenby, R.A. (2009) A Change of Strategy in the War on Cancer. Nature, 459, 508-509.
http://dx.doi.org/10.1038/459508a - 5. Taleb, N. (2010) The Black Swan: The Impact of the Highly Improbable. Random House Trade Paperbacks, xxxiii, New York, 444 p.
- 6. Gillies, R.J., Verduzco, D. and Gatenby, R.A. (2012) Evolutionary Dynamics of Carcinogenesis and Why Targeted Therapy Does Not Work. Nature Reviews Cancer, 12, 487-493.
http://dx.doi.org/10.1038/nrc3298 - 7. Gatenby, R.A., Silva, A.S., Gillies, R.J. and Frieden, B.R. (2009) Adaptive Therapy. Cancer Research, 69, 4894-4903.
http://dx.doi.org/10.1158/0008-5472.CAN-08-3658 - 8. Thompson, J.R. (1980) A Simple Model for Treatment Induced Resistance in Pest Populations and in Metastasized Tumor Systems. In: Kluwer, Ed., Applications of Information and Control Systems, Patras, Greece.
- 9. Cunningham, J.J., Gatenby, R.A. and Brown, J.S. (2011) Evolutionary Dynamics in Cancer Therapy. Molecular Pharmaceutics, 8, 2094-2100.
http://dx.doi.org/10.1021/mp2002279 - 10. Silva, A.S., Kam, Y., Khin, Z.P., Minton, S.E., Gillies, R.J., et al. (2012) Evolutionary Approaches to Prolong Progression-Free Survival in Breast Cancer. Cancer Research, 72, 6362-6370.
http://dx.doi.org/10.1158/0008-5472.CAN-12-2235 - 11. Chmielecki, J., Foo, J., Oxnard, G.R., Hutchinson, K., Ohashi, K., et al. (2011) Optimization of Dosing for EGFR-Mutant Non-Small Cell Lung Cancer with Evolutionary Cancer Modeling. Science Translational Medicine, 3, 90ra59.
http://dx.doi.org/10.1126/scitranslmed.3002356 - 12. Stewart, A.K., Richardson, P.G. and San-Miguel, J.F. (2009) How I Treat Multiple Myeloma in Younger Patients. Blood, 114, 5436-5443.
http://dx.doi.org/10.1182/blood-2009-07-204651 - 13. Palumbo, A. and Gay, F. (2009) How to Treat Elderly Patients with Multiple Myeloma: Combination of Therapy or Sequencing. Hematology, 2009, 566-577.
http://dx.doi.org/10.1182/asheducation-2009.1.566 - 14. Baz, R., Patel, A.M., Ho, V.Q., Shain, K., Alsina, M., et al. (2011) Outcomes Analysis of Doublets of Novel Agents with Corticosteroids Versus Regimens with 3 or More Agents for Multiple Myeloma (MM): A Retrospective Analysis. Blood, 118, 820-820.
- 15. Baz, R., Alsina, M., Shain, K.H., Paleveda, J., Hillgruber, N., et al. (2012) Response Adapted Therapy Using Single Agent Lenalidomide in Older Adults with Newly Diagnosed Standard Risk Multiple Myeloma. Blood, 120.
- 16. Alsina, M., Baz, R., Shain, K.H., Ochoa, L., Nishihori, T., et al. (2012) Updated Results of Phase II Study of Cyclophosphamide(Cy), Bortezomib(Bz), Pegylated Doxorubicin(DOX), and Dexamethasone(dex), (CVDD), in Patients with Newly Diagnosed Myeloma: an Effective Induction Regimen for High Risk Disease. Blood, 120.
- 17. Baz, R., Hussein, M.A., Sullivan, D., Ochoa-Bayona, J.L., Hartley, M.A., et al. (2010) Updated Results of the Phase II Study of Pegylated Liposomal Doxorubicin (PLD), Low Dose Dexamethasone (DEX) and Lenalidomide (LEN) In Patients with Newly Diagnosed (ND) Multiple Myeloma (MM). Blood, 116, 1260-1260.
- 18. Giralt, S. (2011) Stem Cell Transplantation for Multiple Myeloma: Current and Future Status. Hematology, 2011, 191-196.
http://dx.doi.org/10.1182/asheducation-2011.1.191 - 19. Durie, B.G.M., Harousseau, J.L., Miguel, J.S., Blade, J., Barlogie, B., et al. (2006) International Uniform Response Criteria for Multiple Myeloma. Leukemia, 20, 1467-1473.
http://dx.doi.org/10.1038/sj.leu.2404284 - 20. Silva, A.S., Khin, Z., Shain, K.H., Baz, R., Hazlehurst, L.A., et al. (2012) Personalizing Myeloma Chemotherapy Using Evolutionary Computational Models and Ex Vivo Assays. Blood, 120.
- 21. Salmon, S.E., Hamburger, A.W., Soehnlen, B., Durie, B.G., Alberts, D.S., et al. (1978) Quantitation of Differential Sensitivity of Human-Tumor Stem Cells to Anticancer Drugs. The New England Journal of Medicine, 298, 1321-1327.
http://dx.doi.org/10.1056/NEJM197806152982401 - 22. Suggitt, M. and Bibby, M.C. (2005) 50 Years of Preclinical Anticancer Drug Screening: Empirical to Target-Driven Approaches. Clinical Cancer Research, 11, 971-981.
- 23. Sniegowski, P.D., Gerrish, P.J. and Lenski, R.E. (1997) Evolution of High Mutation Rates in Experimental Populations of E. coli. Nature, 387, 703-705.
http://dx.doi.org/10.1038/42701 - 24. Keats, J.J., Chesi, M., Egan, J.B., Garbitt, V.M., Palmer, S.E., Braggio, E., et al. (2012) Clonal Competition with Alternating Dominance in Multiple Myeloma. Blood, 120, 1067-1076.
http://dx.doi.org/10.1182/blood-2012-01-405985 - 25. Kuhnemund, A., Liebisch, P., Bauchmuller, K., zur Hausen, A., Veelken, H., et al. (2009) ‘Light-Chain Escape-Multiple Myeloma’—An Escape Phenomenon from Plateau Phase: Report of the Largest Patient Series Using LC-Monitoring. Journal of Cancer Research and Clinical Oncology, 135, 477-484.
http://dx.doi.org/10.1007/s00432-008-0470-7






